以GM(1, 1)模型为代表的灰色预测模型经过多年的发展与完善,在变形监测领域具有广泛的应用[1-3]。GM(1, 1)模型本质上属于指数函数模型,适合于近似指数序列的建模分析[2-3]。但变形监测数据受地质条件和环境因素的影响,具有多种多样的发展趋势。一般在滑坡临滑阶段[4]或变形体加速变形阶段[5],变形监测数据往往具有指数发展趋势,可用GM(1, 1)模型进行分析预测;而路基或地基沉降往往具有S型变化趋势,并且沉降一般会逐渐趋于稳定,这种情况下GM(1, 1)模型是不适用的。当沉降趋于稳定或具有S型变化趋势时,可采用Verhulst、Richards、Usher、Weibull等生长曲线模型进行分析预测。如果采用灰色建模法,又可将Verhulst模型称作灰色Verhulst模型[6]。GM(1, 1)幂模型是一类非线性灰色模型,随着参数α取值的不同,该模型可用于不同类型的原始序列建模[7]。当α=0时,GM(1, 1)幂模型即为GM(1, 1)模型;当α=2时,GM(1, 1)幂模型即为灰色Verhulst模型。对比GM(1, 1)幂模型的时间响应式与沉降预测常用的Richards模型表达式[8]可知,两者具有一致性,区别只是GM(1, 1)幂模型采用的是灰色系统理论的参数求解方法,所以可称之为灰色Richards模型。鉴于GM(1, 1)幂模型与Richards模型的一致性,本文将其应用到沉降预测中;考虑到GM(1, 1)幂模型存在一些不足之处,本文对其进行改进;最后,提出该模型的应用建议。
1 GM(1, 1)幂模型的改进 1.1 GM(1, 1)幂模型的建模原理令x(0)为GM(1, 1)幂模型的建模原始序列:
| $ {X^{^{\left( 0 \right)}}} = \left( {{x^{^{\left( 0 \right)}}}\left( 1 \right),{x^{^{\left( 0 \right)}}}\left( 2 \right), \cdots {x^{^{\left( 0 \right)}}}\left( n \right)} \right) $ | (1) |
其一次累加序列为:
| $ {X^{^{\left( 1 \right)}}} = \left( {{x^{^{\left( 1 \right)}}}\left( 1 \right),{x^{^{\left( 1 \right)}}}\left( 2 \right), \cdots {x^{^{\left( 1 \right)}}}\left( n \right)} \right) $ | (2) |
定义
| $ {x^{^{\left( 0 \right)}}}\left( k \right) + a{z^{^{\left( 1 \right)}}}\left( k \right) = b{\left( {{z^{^{\left( 1 \right)}}}\left( k \right)} \right)^\alpha } $ | (3) |
为GM(1, 1)幂模型。式中,a为发展系数,b为灰作用量,α为模型参数,z(1)(k)=0.5(x(1)(k)+x(1)(k-1))。
以最小二乘法确定参数:
| $ {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} = {\left( {\boldsymbol{B}{^{\rm{T}}}\boldsymbol{B}} \right)^{ - 1}}{\boldsymbol{B}^{\rm{T}}}\boldsymbol{Y} $ | (4) |
式中,
| $ \boldsymbol{B} = \left[ {\begin{array}{*{20}{c}} { - {z^{\left( 1 \right)}}\left( 2 \right)}&{{{\left( {{z^{\left( 1 \right)}}\left( 2 \right)} \right)}^\alpha }}\\ { - {z^{\left( 1 \right)}}\left( 3 \right)}&{{{\left( {{z^{\left( 1 \right)}}\left( 3 \right)} \right)}^\alpha }}\\ \vdots & \vdots \\ { - {z^{\left( 1 \right)}}\left( n \right)}&{{{\left( {{z^{\left( 1 \right)}}\left( 4 \right)} \right)}^\alpha }} \end{array}} \right],\boldsymbol{Y} = \left[ {\begin{array}{*{20}{c}} {{x^{^{\left( 0 \right)}}}\left( 2 \right)}\\ {{x^{^{\left( 0 \right)}}}\left( 3 \right)}\\ \vdots \\ {{x^{^{\left( 0 \right)}}}\left( n \right)} \end{array}} \right] $ | (5) |
GM(1, 1)幂模型的白化方程为:
| $ \frac{{{\rm{d}}{x^{^{\left( 1 \right)}}}\left( t \right)}}{{{\rm{d}}t}} + a{x^{^{\left( 1 \right)}}}\left( t \right) = b{\left( {{x^{^{\left( 1 \right)}}}\left( t \right)} \right)^\alpha } $ | (6) |
GM(1, 1)幂模型的时间响应式为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \\ {\left\{ {\left[ {{x^{^{\left( 1 \right)}}}{{\left( 1 \right)}^{1 - \alpha }} - \frac{b}{a}} \right]{{\rm{e}}^{ - \left( {1 - \alpha } \right)a\left( {k - 1} \right)}} + \frac{b}{a}} \right\}^{\frac{1}{{1 - \alpha }}}} \end{array} $ | (7) |
还原值为:
| $ {\kern 1pt} \left\{ \begin{array}{l} {{\hat x}^{^{\left( 0 \right)}}}\left( 1 \right) = {x^{^{\left( 0 \right)}}}\left( 1 \right)\\ {{\hat x}^{^{\left( 0 \right)}}}\left( k \right) = {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) - {{\hat x}^{^{\left( 1 \right)}}}\left( {k - 1} \right),k = 2,3, \cdots n \end{array} \right. $ | (8) |
对比GM(1, 1)幂模型时间响应式(7)与Richards模型的表达式[8]可见,两者具有一致性,可称之为灰色Richards模型。若采用直接建模法[9],则可用于S型沉降的全过程预测;若采用累加建模,则适用于呈现单峰特点的原始序列建模。本文研究沉降预测问题,所以仅讨论直接建模情况下的GM(1, 1)幂模型和GM(1, 1)模型。
在0 < α < 1且a > 0和α>1且a < 0两种情况下,GM(1, 1)幂模型与灰色Verhulst模型具有相同的极限性质,即存在极限值,但GM(1, 1)幂模型的拟合精度高于灰色Verhulst模型[7]。对于GM(1, 1)幂模型解的性质详见文献[7],本文不再详述。
1.2 GM(1, 1)幂模型的不足之处与改进方法 1.2.1 灰色建模的固有缺陷及改进GM(1, 1)幂模型同GM(1, 1)模型一样,也存在背景值构造缺陷。从上述GM(1, 1)幂模型的建模原理可以看出,其同样采用的是均值背景值公式,与实际背景值不符,使得模型不具备无偏性[10]。
对式(7)两边同时取1-α次方可得:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {{{\hat x}^{^{\left( 1 \right)}}}\left( k \right)} \right)^{1 - \alpha }} = \\ \left[ {{x^{^{\left( 1 \right)}}}{{\left( 1 \right)}^{1 - \alpha }} - \frac{b}{a}} \right]{{\rm{e}}^{ - \left( {1 - \alpha } \right)a\left( {k - 1} \right)}} + \frac{b}{a} \end{array} $ | (9) |
式(9)右边恰好为关于k的非齐次指数函数,而GM(1, 1)模型的时间响应式即为关于k的非齐次指数函数。目前,GM(1, 1)模型的无偏建模已经实现,因此,可以通过对X(1)进行(x(1)(k))1-α幂函数变换,再建立无偏GM(1, 1)模型以实现GM(1, 1)幂模型的无偏建模。这比改进GM(1, 1)幂模型的背景值[11]或者灰导数[10]更为直接。无偏GM(1, 1)模型的建立方法有多种,比如离散GM(1, 1)模型[12]、背景值构造改进的GM(1, 1)模型[13]、白化方程参数重构的GM(1, 1)模型[14]。基于白化方程参数重构的GM(1, 1)模型仅通过白化方程与灰微分方程之间的参数变换实现模型的无偏性,保留了灰色模型建模原理简单的特征[2]。本文以其作为基本模型,通过幂函数变换建立无偏GM(1, 1)幂模型。采用直接建模法,其建模原理如下。
令X(1)为沉降监测序列,幂函数变换后的序列为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} X{'^{\left( 1 \right)}} = {\left( {{X^{\left( 1 \right)}}} \right)^{1 - \alpha }} = \\ \left( {{{\left( {{x^{\left( 1 \right)}}\left( 1 \right)} \right)}^{1 - \alpha }},{{\left( {{x^{\left( 1 \right)}}\left( 2 \right)} \right)}^{1 - \alpha }}, \cdots {{\left( {{x^{\left( 1 \right)}}\left( n \right)} \right)}^{1 - \alpha }}} \right) \end{array} $ | (10) |
其中,α≠1。
其一次累减序列为:
| $ X{'^{\left( 0 \right)}} = \left( {x{'^{\left( 0 \right)}}\left( 1 \right),x{'^{\left( 0 \right)}}\left( 2 \right), \cdots x{'^{\left( 0 \right)}}\left( n \right)} \right) $ | (11) |
根据无偏GM(1, 1)模型的灰微分方程:
| $ x{'^{\left( 0 \right)}}\left( k \right) + az{'^{\left( 1 \right)}}\left( k \right) = b $ | (12) |
式中,a为发展系数,b为灰作用量,z′(1)(k)=0.5(x′(1)(k)+x′(1)(k-1))。
以最小二乘法确定参数:
| $ {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} = {\left( {\boldsymbol{B}{^{\rm{T}}}\boldsymbol{B}} \right)^{ - 1}}{\boldsymbol{B}^{\rm{T}}}\boldsymbol{Y} $ | (13) |
式中,
| $ \boldsymbol{B} = \left[ {\begin{array}{*{20}{c}} { - z{'^{\left( 1 \right)}}\left( 2 \right)}&1\\ { - z{'^{\left( 1 \right)}}\left( 3 \right)}&1\\ \vdots & \vdots \\ { - z{'^{\left( 1 \right)}}\left( n \right)}&1 \end{array}} \right],\boldsymbol{Y} = \left[ {\begin{array}{*{20}{c}} {x{'^{^{\left( 0 \right)}}}\left( 2 \right)}\\ {x{'^{^{\left( 0 \right)}}}\left( 3 \right)}\\ \vdots \\ {x{'^{^{\left( 0 \right)}}}\left( n \right)} \end{array}} \right] $ | (14) |
白化方程为:
| $ \frac{{{\rm{d}}x{'^{^{\left( 1 \right)}}}\left( t \right)}}{{{\rm{d}}t}} + mx{'^{^{\left( 1 \right)}}}\left( t \right) = n $ | (15) |
时间响应式为:
| $ \hat x{'^{^{\left( 1 \right)}}}\left( k \right) = \left( {x{'^{^{\left( 1 \right)}}}\left( 1 \right) - \frac{n}{m}} \right){{\rm{e}}^{ - m\left( {k - 1} \right)}} + \frac{n}{m} $ | (16) |
其中,参数m、n按式(17)计算:
| $ m = \ln \frac{{2 + a}}{{2 - a}},n = \frac{b}{a}m $ | (17) |
将预测值
| $ \begin{array}{l} \hat x{'^{^{\left( 1 \right)}}}\left( k \right) = \\ {\left\{ {\left[ {{{\left( {{x^{^{\left( 1 \right)}}}\left( 1 \right)} \right)}^{1 - \alpha }} - \frac{n}{m}} \right]{{\rm{e}}^{ - m\left( {k - 1} \right)}} + \frac{n}{m}} \right\}^{\frac{1}{{1 - \alpha }}}} \end{array} $ | (18) |
实际工程中的沉降监测数据大多具有非等时间间隔的性质,这种情况下GM(1, 1)幂模型同GM(1, 1)模型一样不能直接使用。由幂函数变换结合无偏GM(1, 1)模型可建立无偏GM(1, 1)幂模型,同样,幂函数变换加上非等间隔无偏GM(1, 1)模型也可建立非等间隔无偏GM(1, 1)幂模型。文献[3]中提出了一种可用于具有近似指数趋势数据建模的非等间隔无偏GM(1, 1)模型。本文以其作为基本模型,通过幂函数变换建立非等间隔无偏GM(1, 1)幂模型。采用直接建模法,其建模原理如下。
令X(1)为沉降监测序列,幂函数变换后的序列为:
| $ \begin{array}{l} X{'^{\left( 1 \right)}} = {\left( {{X^{\left( 1 \right)}}} \right)^{1 - \alpha }} = \\ \left( {{{\left( {{x^{\left( 1 \right)}}\left( 1 \right)} \right)}^{1 - \alpha }},{{\left( {{x^{\left( 1 \right)}}\left( 2 \right)} \right)}^{1 - \alpha }}, \cdots {{\left( {{x^{\left( 1 \right)}}\left( n \right)} \right)}^{1 - \alpha }}} \right) \end{array} $ | (19) |
其中,α≠1。
对应的时间序列为:
| $ {T^{\left( 1 \right)}} = \left( {{t^{\left( 1 \right)}}\left( 1 \right),{t^{\left( 1 \right)}}\left( 2 \right), \cdots {t^{\left( 1 \right)}}\left( n \right)} \right) $ | (20) |
上述序列的一次累减值为:
| $ X{'^{\left( 0 \right)}} = \left( {x{'^{\left( 0 \right)}}\left( 1 \right),x{'^{\left( 0 \right)}}\left( 2 \right), \cdots x{'^{\left( 0 \right)}}\left( n \right)} \right) $ | (21) |
| $ {T^{\left( 0 \right)}} = \left( {{t^{\left( 0 \right)}}\left( 1 \right),{t^{\left( 0 \right)}}\left( 2 \right), \cdots {t^{\left( 0 \right)}}\left( n \right)} \right) $ | (22) |
白化方程为:
| $ \frac{{{\rm{d}}x{'^{^{\left( 1 \right)}}}\left( t \right)}}{{{\rm{d}}t}} + ax{'^{^{\left( 1 \right)}}}\left( t \right) = b $ | (23) |
时间响应序列为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat x{'^{^{\left( 1 \right)}}}\left( k \right) = \left( {x{'^{^{\left( 1 \right)}}}\left( 1 \right) - \frac{b}{a}} \right) \cdot \\ \exp \left( { - a\left( {{t^{\left( 1 \right)}}\left( k \right) - {t^{\left( 1 \right)}}\left( 1 \right)} \right)} \right) + \frac{b}{a} \end{array} $ | (24) |
对应的灰微分方程为:
| $ \frac{{x{'^{\left( 0 \right)}}\left( k \right)}}{{{t^{\left( 0 \right)}}\left( k \right)}} = az{'^{\left( 1 \right)}}\left( k \right) = b $ | (25) |
式中,z′(1)(k)=px′(1)(k)+(1-p)x′(1)(k-1),
| $ {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} = {\left( {\boldsymbol{B}{^{\rm{T}}}\boldsymbol{B}} \right)^{ - 1}}{\boldsymbol{B}^{\rm{T}}}\boldsymbol{Y} $ | (26) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \boldsymbol{Y} = \left[ {\begin{array}{*{20}{c}} {x{'^{\left( 0 \right)}}\left( 1 \right)}\\ {x{'^{\left( 0 \right)}}\left( 2 \right)}\\ \vdots \\ {x{'^{\left( 0 \right)}}\left( n \right)} \end{array}} \right],\boldsymbol{B} = \\ \left[ {\begin{array}{*{20}{c}} {{t^{\left( 0 \right)}}\left( 2 \right)}&0&0&0\\ 0&{{t^{\left( 0 \right)}}\left( 3 \right)}&0&0\\ 0&0& \vdots &0\\ 0&0&0&{{t^{\left( 0 \right)}}\left( n \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - z{'^{^{\left( 1 \right)}}}\left( 2 \right)}&1\\ { - z{'^{^{\left( 1 \right)}}}\left( 3 \right)}&1\\ \vdots & \vdots \\ { - z{'^{^{\left( 1 \right)}}}\left( n \right)}&1 \end{array}} \right] \end{array} $ | (27) |
将预测值
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \left\{ {\left[ {{{\left( {{x^{^{\left( 1 \right)}}}\left( 1 \right)} \right)}^{1 - \alpha }} - \frac{b}{a}} \right] \cdot } \right.\\ {\left. {\exp \left( { - a\left( {{t^{\left( 1 \right)}}\left( k \right) - {t^{\left( 1 \right)}}\left( 1 \right)} \right)} \right) + \frac{b}{a}} \right\}^{\frac{1}{{1 - \alpha }}}} \end{array} $ | (28) |
与无偏GM(1, 1)模型相比,无偏GM(1, 1)幂模型增加了参数α的求解,非等间隔无偏GM(1, 1)幂模型则增加了参数α、β的求解。如果采用不断尝试的方法确定最优参数α或β,则需要重复大量的矩阵运算,所以一般都会借助Lingo、Matlab等软件编程运算[10-11]。本文选用Matlab作为计算工具,根据无偏GM(1, 1)幂模型和非等间隔无偏GM(1, 1)幂模型的建模原理编制Matlab程序,以拟合结果的平均相对误差最小作为优化目标,以Matlab直接搜索工具箱(pattern search tool)确定最优参数α或β。
由于GM(1, 1)幂模型可称为灰色Richards模型,所以可以直接使用Richards模型代替GM(1, 1)幂模型。Origin软件不需要考虑数据量和变形监测时间间隔,只要学会拟合操作即可,复杂的迭代过程交由Origin软件处理,比灰色预测模型更为实用[2]。Origin软件中提供了Richards模型的自带拟合函数SRichards2,其表达式如下:
| $ y = a{\left[ {1 + \left( {d - 1} \right){{\rm{e}}^{ - k\left( {x - {x_c}} \right)}}} \right]^{1/\left( {1 - d} \right)}} $ | (29) |
式中,a、d、k、xc为模型参数。
将上式作为GM(1, 1)幂模型的替代建模方法,可避免复杂的矩阵运算和参数优化求解,且不用考虑数据的非等间隔性而分别建模。
2 工程实例应用及建议 2.1 实例1以邵阳-怀化高速公路某软土路基断面12期的总体沉降板实测值为例[15]。沉降的发展有趋于稳定的趋势,可用无偏GM(1, 1)幂模型和Richards模型进行分析预测。分别建立无偏GM(1, 1)幂模型和Origin拟合函数SRichards2。
无偏GM(1, 1)幂模型:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \\ {\left( {0.365{\kern 1pt} {\kern 1pt} {\kern 1pt} 7{{\rm{e}}^{ - 0.477{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\left( {k - 1} \right)}} + 0.232{\kern 1pt} {\kern 1pt} {\kern 1pt} 2} \right)^{ - 2.463{\kern 1pt} {\kern 1pt} {\kern 1pt} 3}} \end{array} $ | (30) |
当k→∞时,预测沉降极限值
SRichards2:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \\ {\left( {0.326{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{{\rm{e}}^{ - 0.422{\kern 1pt} {\kern 1pt} {\kern 1pt} 4\left( {k - 1} \right)}} + 0.384{\kern 1pt} {\kern 1pt} {\kern 1pt} 5} \right)^{ - 3.786{\kern 1pt} {\kern 1pt} {\kern 1pt} 7}} \end{array} $ | (31) |
当k→∞时,预测沉降极限值
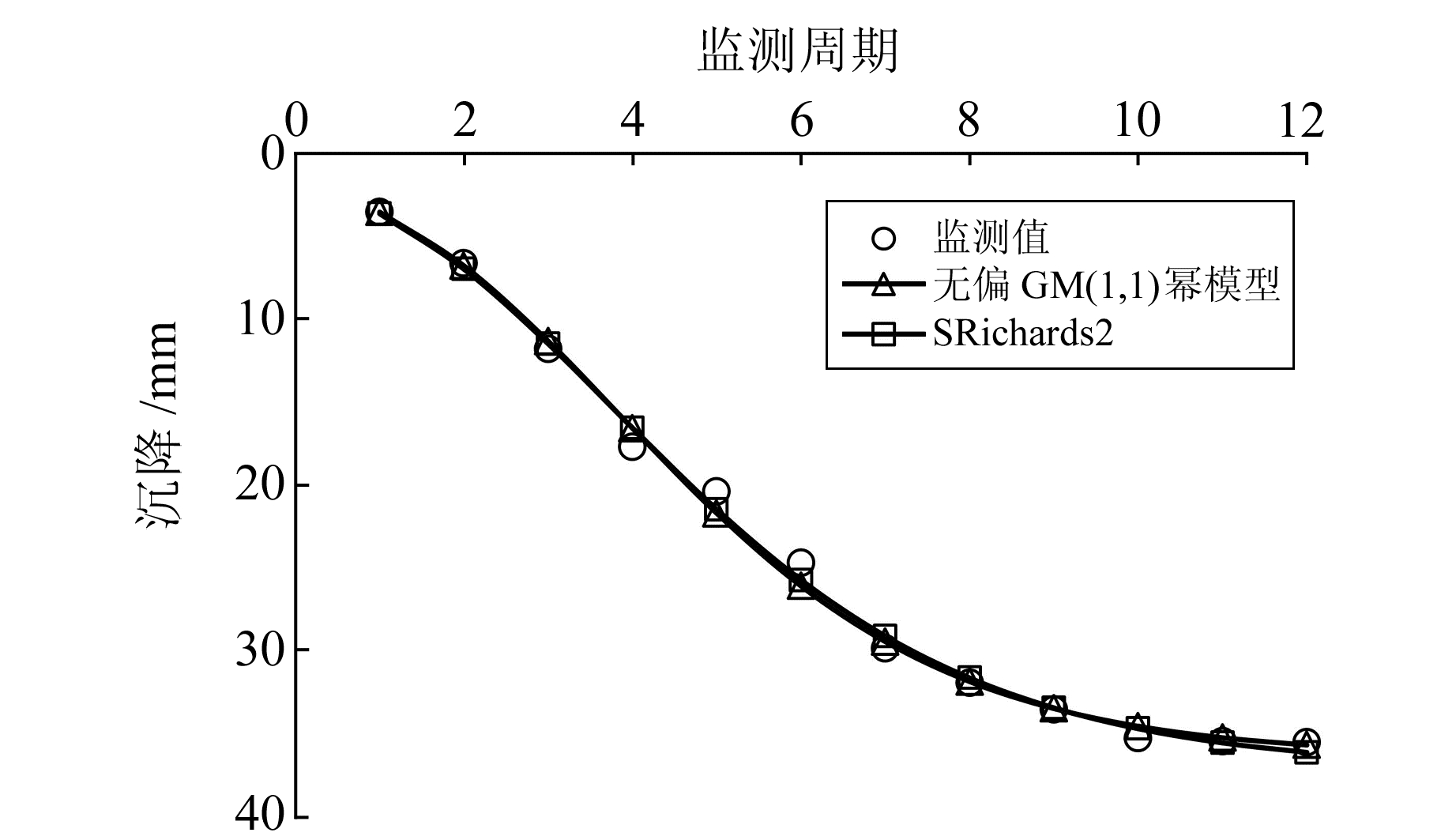
两种方法的拟合结果见图 1,拟合精度评价见表 1。从图 1可以看出,无偏GM(1, 1)幂模型和SRichards2的拟合结果非常接近,无偏GM(1, 1)幂模型预测沉降极限值为36.47 mm,SRichards2预测沉降极限值为37.31 mm。从表 1看出,两种方法拟合结果的均方误差和平均相对误差的差异较小,对沉降的拟合效果良好。无偏GM(1, 1)幂模型拟合结果的平均相对误差仅为2.44%,比SRichards2的2.81%稍小;SRichards2的拟合结果的均方误差为5.09,稍小于无偏GM(1, 1)幂模型的5.89。无偏GM(1, 1)幂模型和SRichards2的拟合结果和拟合精度都非常接近,说明对于该实例两者的拟合效果相当。
|
图 1 两种方法拟合结果与监测结果的对比 Fig. 1 Comparison of monitoring results and fitting results between the two methods |
|
|
表 1 两种方法拟合精度的评价 Tab. 1 Evaluation of fitting precision of the two methods |
以成绵乐铁路客运专线DK171+600测点观测结果为例[16]。该沉降数据具有非等间隔特征,沉降的发展有趋于稳定的趋势,可用非等间隔无偏GM(1, 1)幂模型和Richards模型进行分析预测。分别建立非等间隔无偏GM(1, 1)幂模型和Origin拟合函数SRichards2。
非等间隔无偏GM(1, 1)幂模型:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \left( { - 0.006{\kern 1pt} {\kern 1pt} {\kern 1pt} 9 \cdot } \right.\\ {\left. {{{\rm{e}}^{ - 0.032{\kern 1pt} {\kern 1pt} {\kern 1pt} 5\left( {{t^{\left( 1 \right)}}\left( k \right) - {t^{\left( 1 \right)}}\left( 1 \right)} \right)}} + 1.008{\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \right)^{161.502{\kern 1pt} {\kern 1pt} {\kern 1pt} 0}} \end{array} $ | (32) |
当t(1)(k)→∞时,预测沉降极限值
SRichards2:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\hat x}^{^{\left( 1 \right)}}}\left( k \right) = \left( { - 0.012{\kern 1pt} {\kern 1pt} {\kern 1pt} 4 \cdot } \right.\\ {\left. {{{\rm{e}}^{ - 0.034{\kern 1pt} {\kern 1pt} {\kern 1pt} 23\left( {{t^{\left( 1 \right)}}\left( k \right) - {t^{\left( 1 \right)}}\left( 1 \right)} \right)}} + 1.014{\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \right)^{91.911{\kern 1pt} {\kern 1pt} {\kern 1pt} 8}} \end{array} $ | (33) |
当t(1)(k)→∞时,预测沉降极限值
式(32)、(33)中,t(1)(1)=27。
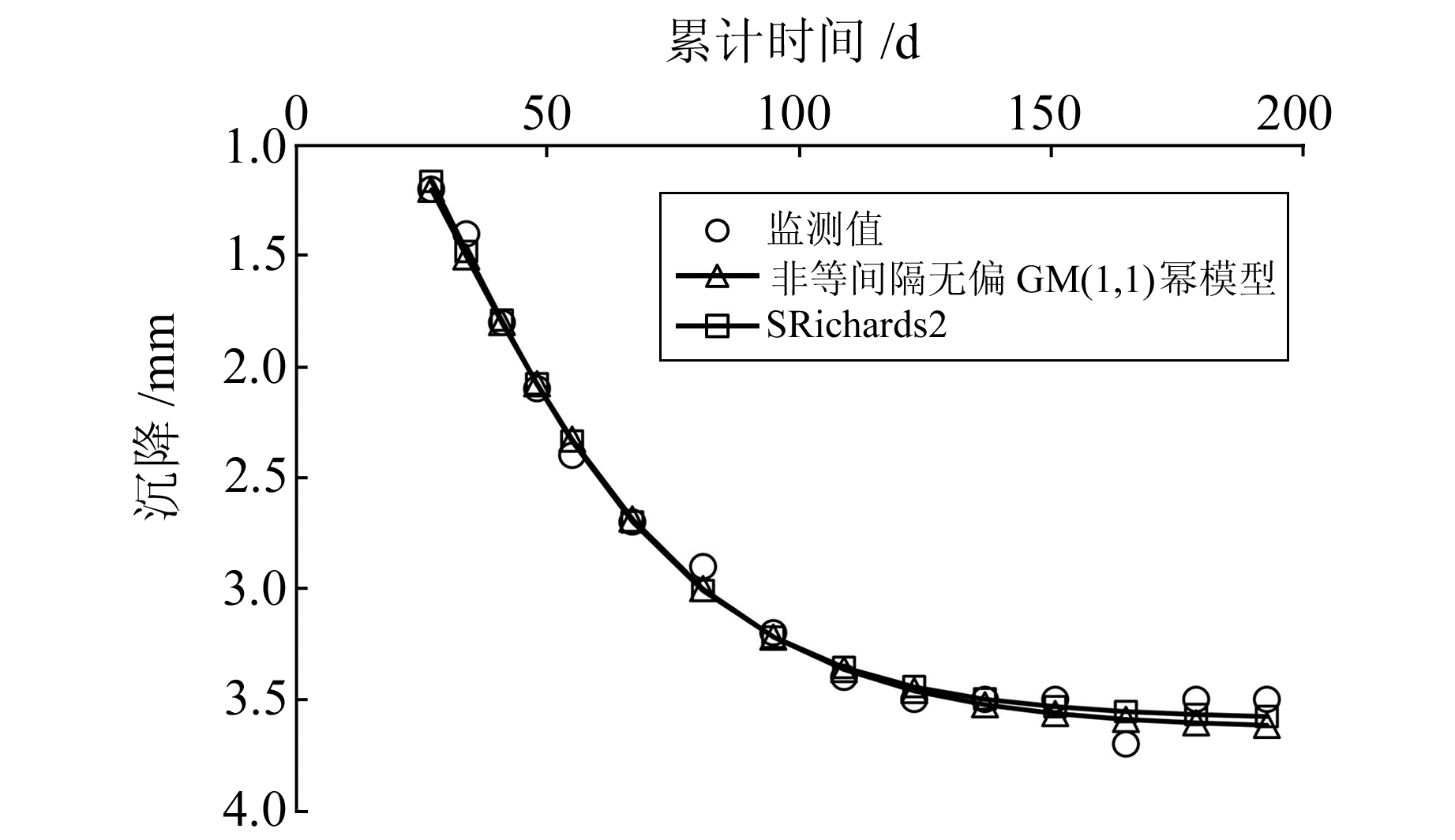
两种方法的拟合结果见图 2,拟合精度评价见表 2。从图 2可以看出,非等间隔无偏GM(1, 1)幂模型和SRichards2的拟合结果同样非常接近。非等间隔无偏GM(1, 1)幂模型预测沉降极限值为3.62 mm,SRichards2预测沉降极限值为3.59 mm。从表 2看出,两种方法拟合结果的均方误差和平均相对误差几乎一致,对沉降的拟合效果良好。非等间隔无偏GM(1, 1)幂模型拟合结果的平均相对误差和均方误差仅为2.00%和0.07,稍大于SRichards2的1.97%和0.06。非等间隔无偏GM(1, 1)幂模型和SRichards2的拟合结果和拟合精度都非常接近,说明对于该实例两者的拟合效果相当。
|
图 2 两种方法拟合结果与监测结果的对比 Fig. 2 Comparison of monitoring results and fitting results between the two methods |
|
|
Tab. 2 Evaluation of fitting precision of the two methods |
上述两个实例的分析结果表明,无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型对沉降的拟合效果良好,与Origin拟合函数SRichards2的拟合效果相当。SRichards2以Origin软件处理复杂的非线性拟合,两个实例中拟合结果的均方误差都小于无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型。无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型均以拟合结果的平均相对误差最小作为优化目标,所以其拟合结果的平均相对误差可小于SRichards2。
Origin拟合操作简单,不需要考虑数据的时间间隔,拟合效果良好。无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型参数求解比较复杂,同样需要借助商业软件进行优化求解。所以,建议人工处理数据时采用Origin拟合函数SRichards2代替无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型使用。
无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型是以Matlab编程求解,虽然求解过程比较复杂,但是其优化目标可以根据实际情况进行调整,比如可以建立本文应用的平均相对误差,或者考虑数据新旧程度的目标误差函数[17]。所以,对于有特殊优化目标的情况下,可采用本文建立的无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型。
本文所提供的GM(1, 1)幂模型改进方法需要借助Matlab编程或Origin实现变形监测数据的分析和预测。在具有大量监测数据的情况下,若人工进行编程设计或拟合操作,难以满足高效率的管理需求。Origin虽然可以通过Origin C语言进行编程开发以实现数据的自动处理[18],但相比之下Matlab功能更强大,后者已广泛应用于变形监测的自动化和可视化设计[19-20]。所以,若涉及到自动化监测设计,建议采用无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型。
3 结语GM(1, 1)幂模型存在灰色建模的固有缺陷、非等间隔数据的不适用性和参数求解复杂性等不足之处。结合幂函数变换、无偏GM(1, 1)模型和非等间隔无偏GM(1, 1)模型,本文建立了无偏GM(1, 1)幂模型和非等间隔无偏GM(1, 1)幂模型,可用于沉降预测。
基于Matlab程序,以拟合结果的平均相对误差最小作为优化目标,本文提出无偏GM(1, 1)幂模型和非等间隔无偏GM(1, 1)幂模型的参数优化求解方法。鉴于其求解过程较为复杂,同时提出采用Origin拟合函数SRichards2的替代方法。结果显示,两种方法拟合效果相当,均可用于沉降预测。
Origin拟合操作简单,不需要考虑数据的时间间隔,拟合效果良好;无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型以Matlab编程求解,优化目标可以根据实际需要编程设计。从实用的角度出发,建议人工处理数据时采用Origin拟合函数SRichards2;而对于有特殊优化目标的情况或自动化监测设计时,可采用本文建立的无偏GM(1, 1)幂模型与非等间隔无偏GM(1, 1)幂模型。
| [1] |
李克昭, 李志伟, 孟福军. 基于综合优化GM(1, 1)的形变预测模型[J]. 大地测量与地球动力学, 2016, 36(2): 120-123 (Li Kezhao, Li Zhiwei, Meng Fujun. Deformation Forecasting Model Based on Synthetic and Optimized GM(1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 120-123)
(  0) 0) |
| [2] |
陈鹏宇. 无偏灰色模型和Origin拟合函数在变形监测预报中的对比应用[J]. 大地测量与地球动力学, 2017, 37(3): 240-245 (Chen Pengyu. Comparison and Application of Unbiased Grey Model and Origin Fitting Functions on Deformation Monitoring and Prediction[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 240-245)
(  0) 0) |
| [3] |
陈鹏宇. 非等距GM(1, 1)模型在沉降预测中的应用探讨[J]. 大地测量与地球动力学, 2017, 37(7): 709-714 (Chen Pengyu. Discussion of the Application of Non-Equidistant GM(1, 1) Models in Subsidence Prediction[J]. Journal of Geodesy and Geodynamics, 2017, 37(7): 709-714)
(  0) 0) |
| [4] |
肖云, 周春梅, 虞珏, 等. 大冶铁矿滑坡预测模型研究[J]. 武汉工程大学学报, 2010, 32(1): 9-11 (Xiao Yun, Zhou Chunmei, Yu Jue, et al. Study on Prediction Model in Hubei Daye Iron Mine Slope[J]. Journal of Wuhan Institute of Technology, 2010, 32(1): 9-11 DOI:10.3969/j.issn.1674-2869.2010.01.004)
(  0) 0) |
| [5] |
彭正明, 王腾军, 曹冬冬, 等. GM(1, 1)模型的改进及其在变形预测中的应用[J]. 地球科学与环境学报, 2012, 34(4): 102-106 (Peng Zhengming, Wang Tengjun, Cao Dongdong, et al. Improvement of GM(1, 1) Model and Its Application on Deformation Prediction[J]. Journal of Earth Sciences and Environment, 2012, 34(4): 102-106 DOI:10.3969/j.issn.1672-6561.2012.04.014)
(  0) 0) |
| [6] |
肖霞林. 路基沉降变形评估与非等间隔灰色Verhulst模型[J]. 铁道建筑, 2011(4): 86-88 (Xiao Xialin. Assessment of Subgrade Settlement Deformation and Non-Equal Interval Grey Verhulst Model[J]. Railway Engineering, 2011(4): 86-88)
(  0) 0) |
| [7] |
王正新, 党耀国, 刘思峰, 等. GM(1, 1)幂模型求解方法及其解的性质[J]. 系统工程与电子技术, 2009, 31(10): 2 380-2 383 (Wang Zhengxin, Dang Yaoguo, Liu Sifeng, et al. Solution of GM(1, 1) Power Model and Its Properties[J]. Systems Engineering and Electronics, 2009, 31(10): 2 380-2 383)
(  0) 0) |
| [8] |
肖治宇, 陈昌富. 软土路基沉降预测Richards模型方法[J]. 公路交通科技, 2008, 25(11): 29-32 (Xiao Zhiyu, Chen Changfu. Settlement Prediction of Soft Clay Roadbed Based on Richards Model[J]. Journal of Highway and Transportation Research and Development, 2008, 25(11): 29-32 DOI:10.3969/j.issn.1002-0268.2008.11.007)
(  0) 0) |
| [9] |
陈鹏宇, 段新胜. 无偏直接PGM(1, 1)模型及其优化[J]. 三峡大学学报:自然科学版, 2009, 31(5): 66-68 (Chen Pengyu, Duan Xinsheng. Unbiased Direct PGM(1, 1) and Its Optimization[J]. Journal of China Three Gorges University:Natural Sciences, 2009, 31(5): 66-68)
(  0) 0) |
| [10] |
李树峰, 陈鹏宇. 无偏GM(1, 1)幂模型及其应用[J]. 统计与信息论坛, 2010, 25(11): 7-10 (Li Shufeng, Chen Pengyu. Unbiased GM(1, 1) Power Model and Its Application[J]. Statistics and Information Forum, 2010, 25(11): 7-10 DOI:10.3969/j.issn.1007-3116.2010.11.002)
(  0) 0) |
| [11] |
王正新, 党耀国, 赵洁珏. 优化的GM(1, 1)幂模型及其应用[J]. 系统工程理论与实践, 2012, 32(9): 1 973-1 978 (Wang Zhengxin, Dang Yaoguo, Zhao Jiejue. Optimized GM(1, 1) Power Model and Its Application[J]. Systems Engineering-Theory & Practice, 2012, 32(9): 1 973-1 978)
(  0) 0) |
| [12] |
谢乃明, 刘思峰. 离散GM(1, 1)模型与灰色预测模型建模机理[J]. 系统工程理论与实践, 2005, 25(1): 93-99 (Xie Naiming, Liu Sifeng. Discrete GM(1, 1) and Mechanism of Grey Forecasting Model[J]. Systems Engineering-Theory & Practice, 2005, 25(1): 93-99 DOI:10.3321/j.issn:1000-6788.2005.01.014)
(  0) 0) |
| [13] |
陈鹏宇, 段新胜. 基于离散指数函数优化GM(1, 1)模型的重新优化[J]. 三峡大学学报:自然科学版, 2010, 32(1): 88-91 (Chen Pengyu, Duan Xinsheng. Re-Optimizing an Optimal GM(1, 1) Model Based on Discrete Function with Exponential Law[J]. Journal of Three Gorges University:Natural Sciences, 2010, 32(1): 88-91)
(  0) 0) |
| [14] |
Chen P Y, Yu H M, Xie K. GM(1, 1) Model Based on Optimum Parameters of Whitenization Differential Equation and Its Application on Displacement Forecasting of Foundation Pit[J]. The Journal of Grey System, 2013, 25(1): 54-62
(  0) 0) |
| [15] |
唐利民, 朱建军. 软土路基沉降泊松模型的正则化牛顿迭代法[J]. 武汉大学学报:信息科学版, 2013, 38(1): 69-73 (Tang Limin, Zhu Jianjun. Regularized Newton Iterative Algorithm for Poisson Model of Soft Clay Embankment Settlement[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 69-73)
(  0) 0) |
| [16] |
牛欣欣. 路基沉降预测的非等间隔Asaoka法[J]. 公路工程, 2013, 38(6): 241-244 (Niu Xinxin. Non-Equal Interval Asaoka Method for Predicting Subgrade Settlement[J]. Highway Engineering, 2013, 38(6): 241-244)
(  0) 0) |
| [17] |
曹文贵, 印鹏, 贺敏, 等. 考虑实测数据新旧程度的工后沉降单项模型预测方法[J]. 水文地质工程地质, 2015, 42(6): 65-70 (Cao Wengui, Yin Peng, He Min, et al. A Prediction Method for Post-Construction Settlement of a Single Model with the Consideration of the New or Old Degree of the Measured Data[J]. Hydrogeology and Engineering Geology, 2015, 42(6): 65-70)
(  0) 0) |
| [18] |
覃桂菊. 用Origin C编程自动化处理制动试验数据[J]. 铁道机车车辆, 2005, 25(5): 28-30 (Qin Guiju. Automatically Processing Brake Running Test Data with Origin C Program[J]. Railway Locomotive and Car, 2005, 25(5): 28-30)
(  0) 0) |
| [19] |
秦浩, 李同春, 唐繁, 等. 基于MATLAB GUI的水电工程安全监测数据处理界面设计[J]. 水利水电技术, 2016, 47(4): 70-74 (Qin Hao, Li Tongchun, Tang Fan, et al. MATLAB GUI-Based Design of Data Processing Interface for Safety Monitoring of Hydropower Project[J]. Water Resources and Hydropower Engineering, 2016, 47(4): 70-74)
(  0) 0) |
| [20] |
孟永东, 许真, 张永瑞. 基于VB与MATLAB编程的边坡监测数据场可视化[J]. 人民长江, 2016, 47(3): 33-36 (Meng Yongdong, Xu Zhen, Zhang Yongrui. Research on Visualization of Slope Monitoring Data Field Based on MATLAB and VB Hybrid Programming[J]. Yangtze River, 2016, 47(3): 33-36)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

