2. 中国科学院大学,北京市玉泉路19号甲,100049
固体潮的变化幅度与地球内部的物性参数密切相关[1]。随着天文学的发展,现已能精确预测在任意时间引潮天体的位置,进而精密计算地球的引潮力[2]。由于已知其确切力源,结合高精度固体潮观测,精确的固体潮汐理论模拟可为地球内部物性参数提供约束[3],也可为进一步了解地球内部圈层耦合机制与动力学过程提供帮助,并为实测高精度的GNSS定位与地球重力场提供精确的潮汐改正[4]。
传统SNERI地球模型固体潮汐响应的计算方法来自于地球自由振荡和地表负荷的研究,方法如下:将三维矢量空间的2阶形变微分方程作球谐分解,引入3个相互正交的独立解函数,采用4阶Runge-Kutta法计算获得径向微分,在地表上让3个独立解函数线性加权求和满足边界条件,最后获得SNERI地球体潮问题的数值解。传统的4阶Runge-Kutta法存在以下几点不足:1)径向步长取值过大时,无法获得高精度解,径向步长取值过小时,容易造成计算误差积累,导致地表Love数计算精度降低,收敛性变差;2)随着球谐阶数的增加,数值积分时会导致数值溢出,破坏独立解的正交性;3)计算精度目前尚未评定。
本研究所用的谱-有限元法能有效克服上述不足,其基本算法为:先用变分原理导出控制方程的弱解形式,再把球型地球剖分为有限数目的球壳,然后在球面上将负荷运动方程作球谐谱展开,在径向上用有限元方法求解。
本文首先用哈密顿变分原理给出地球固体潮控制方程的弱解形式,然后详述用谱-有限元法进行潮汐运动方程数值求解的全过程,最后计算SNERI地球模型的固体潮形变的数值解。将计算结果与同质地球模型的解析解、PREM地球模型的传统4阶Runge-Kutta法数值解以及超导重力仪观测重力潮汐因子进行比较,评定谱-有限元法求解结果的精度,测试算法的收敛性。
1 固体潮控制方程的弱解形式与求解方法 1.1 固体潮控制方程的弱解形式Dahlen等[5]提出自重固体地球自由振荡的哈密顿积分,在不考虑地球自转的情况下可以描述为:
| $ \int _{{t_1}}^{{t_2}}{\varepsilon _k} + {\varepsilon _e} + {\varepsilon _g}{\rm{d}}t = \int _{{t_1}}^{{t_2}}{{\mathscr F}_{{\rm{surf}}}}{\rm{d}}\mathit{t} $ | (1) |
式中,εk、εe、εg分别为频率域内已形变地球相对于静压应力平衡状态下地球的动能、弹性势能和重力势能的变化量,
| $ {\varepsilon _k} = \frac{1}{2}\mathop \smallint \nolimits^ {\rho _0}{\omega ^2}\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}}{\rm{d}}{\mathit{V}_\mathit{S}} $ | (2) |
式中,ω为潮汐分波的频率,VS为固体地球部分。弹性势能εe为无穷小应变
| $ {{\varepsilon }_{\mathit{e}}}=\frac{1}{2}\mathop{\int }^{}\epsilon \text{ }\!\!~\!\!\text{ }:\mathit{\Gamma }:\epsilon \text{ }\!\!~\!\!\text{ d}{{\mathit{V}}_{\mathit{S}}} $ | (3) |
重力势能εg是由地球内部质点的位移u做功造成的整个地球重力势能变化,表达形式为:
| $ \begin{array}{l} {\rm{}}{\varepsilon _g} = \frac{1}{2}\mathop \smallint \nolimits^ {\rho ^0}\mathit{\boldsymbol{u}} \cdot \nabla {\mathit{\Phi }_1} + {\rho ^0}\mathit{\boldsymbol{u}} \cdot \nabla \nabla {\mathit{\Phi }_0} \cdot \mathit{\boldsymbol{u}} + \\ {\mathit{\rho }_0}\mathit{\boldsymbol{u}} \cdot \nabla {\mathit{\Phi }_1} + \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla {\mathit{\Phi }_1} \cdot \nabla {\mathit{\Phi }_1}{\rm{d}}{\mathit{V}_\mathit{S}} \end{array} $ | (4) |
为了使力位Φ1在哈密顿变分中作为独立于位移u的变量,将力位的Poisson方程通过拉格朗日乘子法引入到重力势能εg中,具体形式在式(4)等号右边的后两项中给出。
基于式(1)给出的哈密顿积分,将式中的自由边界项
| $ {{\mathscr F}_{{\rm{surf}}}} = \mathop \smallint \nolimits^ \mathit{\boldsymbol{T}} \cdot \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{u}} + \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla {\mathit{\Phi }_1} \cdot \mathit{\boldsymbol{n}}{\mathit{\Phi }_1} + \mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}{\mathit{\Phi }_1}{\rm{d}}\mathit{S} $ | (5) |
哈密顿原理保证了式(1)是静态的,对于形变位移u、力位Φ1的任意1阶扰动δu,δΦ1存在,式(1)仍然成立,用公式描述为:
| $ \mathit{\delta }{\varepsilon _k} + \delta {\varepsilon _e} + \delta {\varepsilon _g} = \delta {{\mathscr F}_{{\rm{surf}}}} $ | (6) |
式中,δεe与δεg分别为弹性势能εe与重力势能εg的1阶扰动项,Martinec[6]与Tanaka等[7]已经对δεe与δεg的表达式进行了详细描述,这里不再赘述,δεk为动能εk的1阶扰动项,表示为:
| $ \mathit{\delta }{\mathit{\varepsilon }_\mathit{k}} = \mathop \smallint \nolimits^ {\mathit{\rho }_0}{\mathit{\omega }^2}\mathit{\boldsymbol{u}} \cdot \mathit{\delta } \cdot \mathit{\boldsymbol{u}}{\rm{d}}\mathit{V} $ | (7) |
位移与力位的任意1阶扰动δu和δΦ1以式(8)体现在体潮边界条件项中:
| $ \begin{array}{l} \delta {{\mathscr F}_{{\rm{surf}}}} = \mathop \smallint _{\partial B} \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla \mathit{\Phi }_1^ + \delta {\mathit{\Phi }_1}{\rm{d}}\mathit{S} + \mathop \smallint _{{{\rm{\Sigma }}^{ICB}} + {{\rm{\Sigma }}^{CMB}}} \mathit{\boldsymbol{n}} \cdot \\ \tau \cdot \delta \mathit{\boldsymbol{u}} + \left( {\mathit{\boldsymbol{n}} \cdot \nabla {\mathit{\Phi }_1} + \rho _0^ + \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{u}}} \right)\delta {\mathit{\Phi }_1}{\rm{d}}\mathit{S} \end{array} $ | (8) |
式中,
对于液核部分,采用中性分层流体近似,得到液核扰动位变分方程为[8]:
| $ \begin{array}{l} \mathop \smallint \nolimits^ \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla {\mathit{\Phi }_1} \cdot \nabla \delta {\mathit{\Phi }_1} - \frac{{\rho _0^2}}{\lambda }{\mathit{\Phi }_1}\delta {\mathit{\Phi }_1}d{\rm{VL}} - \\ \mathop \smallint _{{{\rm{\Sigma }}^{ICB}} + {{\rm{\Sigma }}^{CMB}}} \nabla \mathit{\Phi }_1^ - \cdot \mathit{\boldsymbol{n}}\delta \mathit{\Phi }_1^ - {\rm{dS}} = 0, \forall {\rm{ \mathsf{ δ} }}{\mathit{\Phi }_1} \in \mathit{V} \end{array} $ | (9) |
式中,VL为液核部分。
在以上潮汐运动方程的变分表达式中,解函数和扰动函数均属于函数空间V,
| $ \mathit{V}\left( \mathit{B} \right): = \left\{ {\mathit{\delta }\mathit{\boldsymbol{u}}, \mathit{\boldsymbol{u}} \in \mathit{W}_2^1{{(B)}^3};{\mathit{\Phi }_1}, \mathit{\delta }{\mathit{\Phi }_1} \in \mathit{W}_2^1\left( \mathit{B} \right)} \right\} $ | (10) |
式中,B为解空间,即为整个地球,W21为Sobolev空间。式(10)要求解函数与扰动函数平方可积,解函数与扰动函数的1阶导数平方可积。相对于固体潮问题的强解必须2阶可导而言,式(10)降低了解的连续性要求,因此称哈密顿变分下的解为弱解。整合上述地球固体部分与液核部分的变分方程,可得到完整的固体潮问题的弱解形式:
| $ \begin{array}{l} \mathop \smallint \nolimits^ {\rho _0}{\omega ^2}\mathit{\boldsymbol{u}} \cdot \delta \mathit{\boldsymbol{u}} + \nabla \mathit{\boldsymbol{u}}:\mathit{\Gamma }:\nabla \delta \mathit{\boldsymbol{u}} + {\rho _0}[\nabla \left( {\mathit{\boldsymbol{u}} \cdot \nabla {\mathit{\Phi }_0}} \right) - \\ \nabla \cdot \mathit{\boldsymbol{u}}\nabla {\mathit{\Phi }_1} + \nabla {\mathit{\Phi }_1}] \cdot \delta \mathit{\boldsymbol{u}} + \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla {\mathit{\Phi }_1} \cdot \nabla \delta {\mathit{\Phi }_1} + \\ {\rho _0}\left( {\mathit{\boldsymbol{u}} \cdot \nabla \delta {\mathit{\Phi }_1}} \right){\rm{d}}{\mathit{V}_\mathit{S}} + {\mathit{\Sigma }^{{\rm{ICB}}}}\rho _0^ + \left( {{\mathit{\Phi }_1} + \mathit{\boldsymbol{u}} \cdot \nabla {\mathit{\Phi }_0}} \right) \cdot \\ \mathit{\boldsymbol{n}} \cdot \delta \mathit{\boldsymbol{u}} + \rho _0^ + \mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}\delta {\mathit{\Phi }_1}{\rm{dS}} + \mathop \smallint \nolimits^ \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla {\mathit{\Phi }_1} \cdot \nabla \delta {\mathit{\Phi }_1} - \\ \frac{{\rho _0^2}}{\lambda }{\mathit{\Phi }_1}\delta {\mathit{\Phi }_1}{\rm{d}}{\mathit{V}_\mathit{L}} - \mathop \smallint _{{\mathit{\Sigma }^{{\rm{ICB}}}}} \rho _0^ - \left( {{\mathit{\Phi }_1} + \mathit{\boldsymbol{u}} \cdot \nabla {\mathit{\Phi }_0}} \right) \cdot \mathit{\boldsymbol{n}} \cdot \mathit{\delta }\mathit{\boldsymbol{u}} + \\ \rho _0^ - \mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}\delta {\mathit{\Phi }_1}{\rm{dS}} = \mathop \smallint _{\partial B} \frac{1}{{4{\rm{ \mathsf{ π} }}G}}\nabla \mathit{\Phi }_1^ + \delta {\mathit{\Phi }_1}{\rm{dS}} \end{array} $ | (11) |
采用传统谱方法进行球层剖分,利用不同阶次解的解耦特性,并与引潮力位的谱分解相结合,可简化边界条件的计算。球层剖分公式为[6]:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( {r, \mathit{\Omega }} \right)}\\ {\delta \mathit{\boldsymbol{u}}\left( {r, \mathit{\Omega }} \right)} \end{array} = \mathop \sum \limits_{j = 1}^\infty \mathop \sum \limits_{m = - j}^j \{ \begin{array}{*{20}{c}} {{U_{jm}}\left( r \right)}\\ {\delta {U_{jm}}\left( r \right)} \end{array}S_{jm}^{ - 1}\left( \mathit{\Omega } \right) + \\ \begin{array}{*{20}{c}} {{V_{jm}}\left( r \right)}\\ {\delta {V_{jm}}\left( r \right)} \end{array}S_{jm}^1\left( \mathit{\Omega } \right) + \begin{array}{*{20}{c}} {{W_{jm}}\left( r \right)}\\ {\delta {W_{jm}}\left( r \right)} \end{array}S_{jm}^0\left( \mathit{\Omega } \right)\} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {{\mathit{\Phi }_1}\left( {r, \mathit{\Omega }} \right)}\\ {\delta {\mathit{\Phi }_1}\left( {r, \mathit{\Omega }} \right)} \end{array} = \mathop \sum \limits_{j = 1}^\infty \mathop \sum \limits_{m = - j}^j \left\{ {\begin{array}{*{20}{c}} {{F_{jm}}\left( r \right)}\\ {\delta {F_{jm}}\left( r \right)} \end{array}{Y_{jm}}\left( \mathit{\Omega } \right)} \right\} $ | (13) |
式中,Yjm(Ω)为标量球谐函数,Sjm-1(Ω)、Sjm1(Ω)、Sjm0(Ω)为矢量球谐函数,Ujm(r)、δUjm(r)、Vjm(r)、δVjm(r)、Wjm(r)、δWjm(r)、Fjm(r)、δFjm(r)为径向函数。在径向上,将地球半径R剖分为P个子区间,在第q个区间内的解函数和试探函数用线性支函数ψq(r)与ψq(r)内插:
| $ {\psi _q}\left( r \right) = \frac{{{r_{q + 1}} - r}}{{{H_q}}}{\rm{, }}{\psi _{q + 1}}\left( r \right) = \frac{{r - {r_q}}}{{{H_q}}}{\rm{, }}q = 1, 2 \cdots P $ | (14) |
式中,rq、rq+1为径向的第q和q+1个节点至球心的长度,Hq=rq+1-rq为第q个区间的长度。同时,第q个区间的弹性参数、初始密度和重力加速度都选取为一常数,这样式(12)~(14)就构建了有限维空间中的解函数和试探函数。分段常数λ、μ、ρ0和g0代入弱解形式(11),便得到线性对角稀疏矩阵系统:
| $ \mathit{\boldsymbol{KX}} = \mathit{\boldsymbol{F}} $ | (15) |
式中,X =(Ujm(r), Vjm(r), Wjm(r), Fjm(r))T为待求解,K为刚度矩阵,F为非齐次项,求解此矩阵方程便可获得弱解问题的解。
2 计算结果与分析 2.1 与同质地球模型解析解的比较传统上采用一组无量纲化的Love数h、l、k分别表征引潮力位作用在实际地球上与作用在假想表层布满海水的刚体地球上的径向位移、横向位移与附加位的比值。地表第j阶Love数hj、lj和kj用式(16)计算:
| $ {h_j} = \frac{{{U_j}\left( \mathit{R} \right)}}{\mathit{R}}, {l_j} = \frac{{{V_j}\left( \mathit{R} \right)}}{\mathit{R}}, {k_j} = - \frac{{{F_j}\left( \mathit{R} \right)}}{{\mathit{R}{g_0}\left( R \right)}} - 1 $ | (16) |
式中,R为地球半径,g0(R)为地表重力值。Uj(R)、Vj(R)、Fj(R)为在地表的径向位移、横向位移、附加位与引潮位之和。为了方便计算,引潮位振幅设为Rg0(R)。
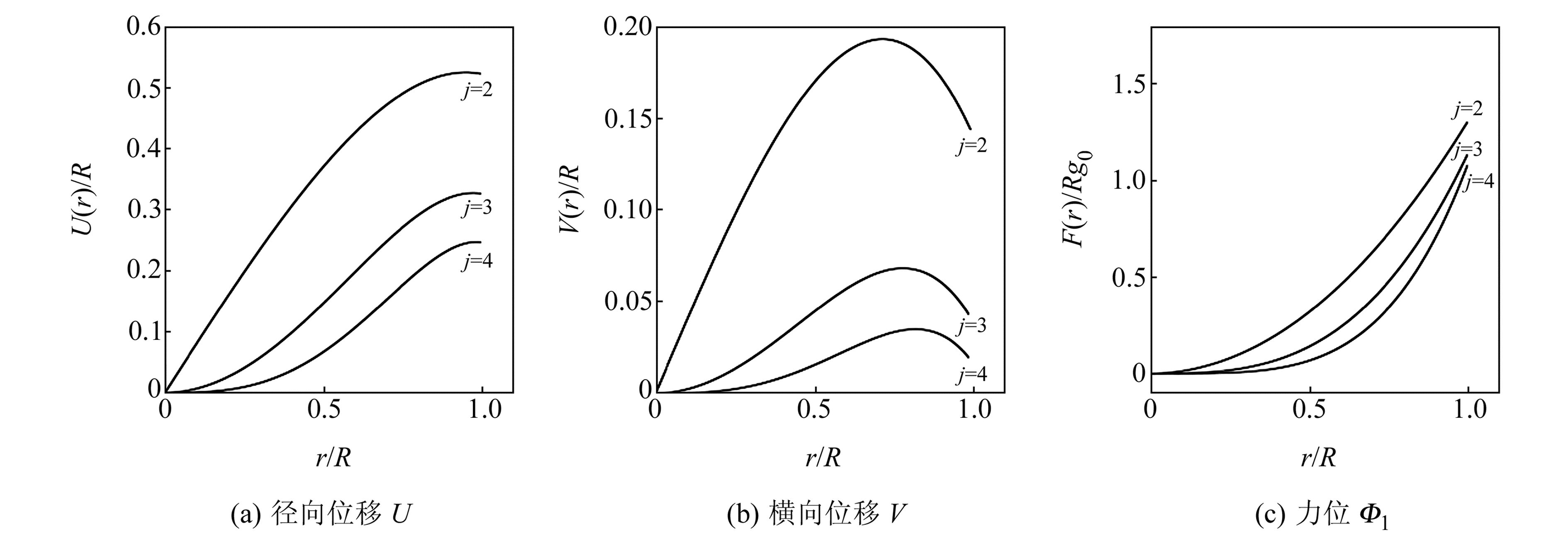
Wu等[9]给出同质地球模型负荷问题的解析解。同质地球为平均地球,模型参数选取如下:密度ρ=5 517 kg/m3, λ=3.528 8×1011N/m2, μ=1.451 9×1011N/m2, 半径R=6.371×106 m。本研究中将Wu等[9]的负荷边界条件替换为体潮边界条件,获得永久固体潮(潮波周期无穷大)的解析解。同质地球模型无量纲2~4阶解析解随径向变化的特征如图 1所示。径向位移Uj起始增速较快,但在近地表处趋于平缓,横向位移Vj同样起始增速很快,但在接近地表之前已达到最大值,附加位与引潮位之和Fj随半径增长其数值和增速都在增加,在地表达到最大值。
|
图 1 无量纲解析解的径向位移U、横向位移V和力位Φ1的径向变化 Fig. 1 The variation of dimensionless radial displacement U, transversal displacement V and gravitational potential perturbation Φ1 over radius in the analytical results |
对于地学领域的科学研究与工程应用,日月引潮位展开至3阶就能满足其精度需求[1],在频率域内,地球对引潮位近似线性响应[10],固体潮Love数计算至3阶已足够描述地球固体潮现象。本研究为充分探明谱-有限元法的数值计算精度与收敛性,将固体潮Love数计算至10阶。表 1左侧给出了同质地球模型2~10阶Love数hj的解析解并保留13位有效数字,右侧给出不同剖分间距的谱-有限元法数值解与解析解结果之差,表中列出的剖分间距分别为100 km、10 km、1 km、0.5 km和0.1 km,由于2个计算结果的差有量级上的差别,同时给出差别的量级,真实的结果之差为对应数值乘以各自的量级。从表 1看出:1)随着径向单元格剖分的细化,数值解的精度持续提高,网格剖分每细化10倍,数值解精度约可提升2个数量级;2)在1 km等间距剖分时,数值解的精度处在10-8量级,在0.1 km等间距剖分时,除h2之外,低阶Love数hj的精度均达到10-10量级。在2~10阶Love数计算过程中,没有出现数据溢出,即使到0.1 km的剖分间距,仍具有良好的收敛性。
|
|
表 1 2~10阶Love数h谱-有限元法数值解与解析解结果比较 Tab. 1 The difference of Love number h of 2nd to 10th degree between spectral-finite element method solutions and analytical solutions |
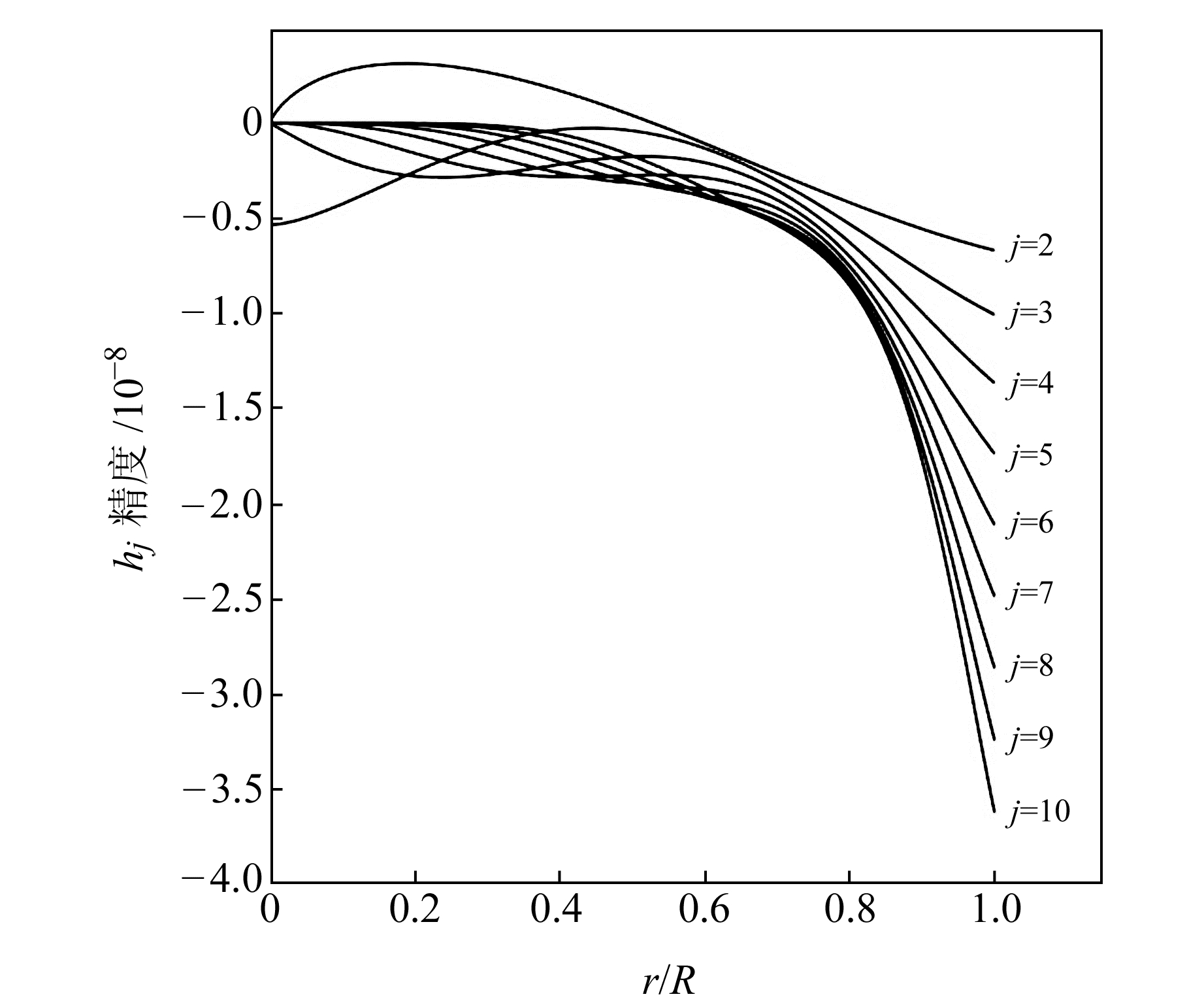
对于目前的固体潮观测来说,利用全球定位系统精密单点定位方法,经过10多年的连续观测,月亮主潮波的水平位移可以确定在0.1 mm的量级[11],换算成Love数l为10-4量级。超导重力仪的观测精度可以达到0.05 μGal,其获得的重力数据经过大气校正与海潮负荷校正后,调和分析得到的主潮波的重力潮汐因子精度为10-5量级[12-13],是目前最精确的固体潮观测,也就是说目前对地球固体潮Love数的观测,精度最高在10-5量级。由表 1可知,100 km剖分间距不能满足观测需要,虽然10 km的剖分间距也高于实测精度,但仅差别1个数量级,因此本研究建议采用1 km剖分间距,比实测精度高约3个数量级。1 km等距剖分的2~10阶Love数hj的计算值与解析解差值的径向变化如图 2所示。可以看出,在地表hj的精度为10-8量级,完全可以满足目前固体潮理论模拟的需求;地球内部数值解的精度均高于在地表值取得的精度,可满足用固体潮高精度地表观测值约束地球内部物性参数与探明地球内部圈层耦合机制与动力学过程的需求。
|
图 2 2~10阶Love数1 km等间距剖分hj与解析解差值径向变化 Fig. 2 The variation of the accuracy of Love numbers among 2nd to 10th degree over the radius in 1 km equispaced node distribution |
为了检验较复杂地球模型下哈密顿变分方法与Galerkin空间离散化方法的适用性,采用Dziewonski等[14]给出的PREM地球模型,按汪汉胜等[15]的方法进行PREM地球模型谱-有限元法体潮Love数的数值计算,即将地壳层(6 356.0~6 368.0 km)与海水层(6 368.0~6 371.0 km)合并为均一弹性层,密度取均值ρ=2 283.4 kg/m3,拉梅参数取μ=2.663 4×1011N/m2,λ=3.421 6×1011N/m2。低阶地表体潮Love数计算结果表明,地表体潮Love数存在极弱的频率依赖性,随着频率的增加,hj、kj和lj均有微弱的增大趋势;随着阶数的增高,体潮Love数hj、kj和lj皆显著减小。
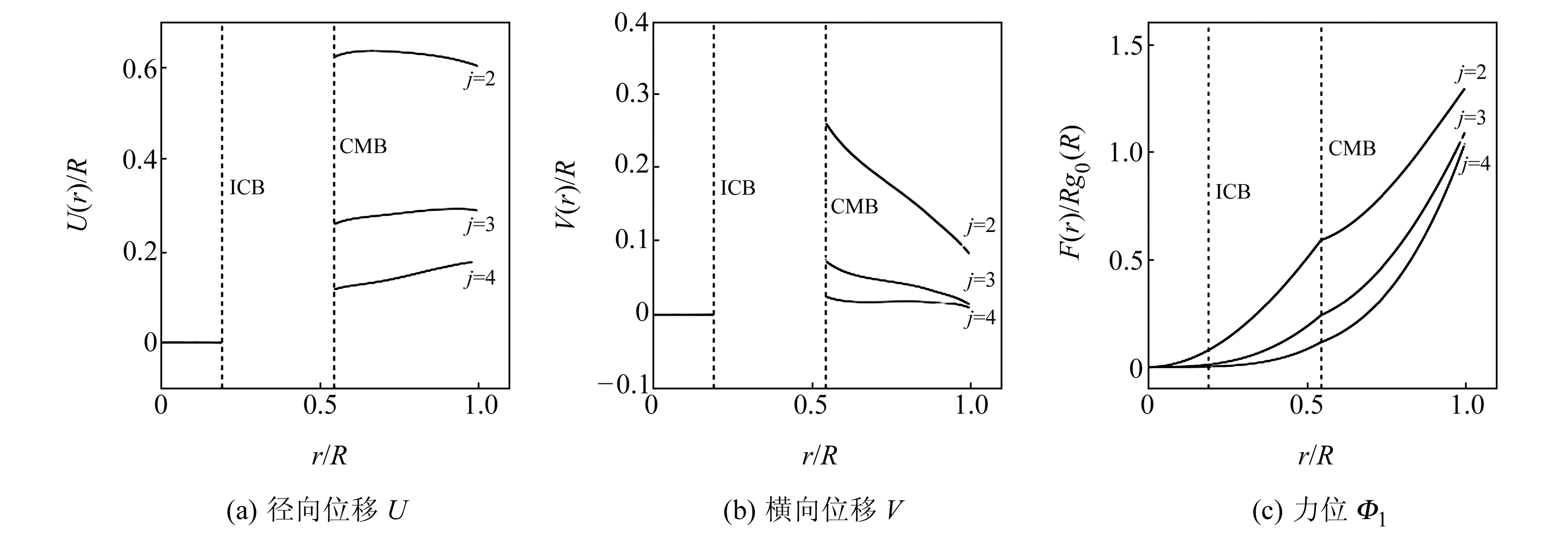
为了解PREM地球模型地球内部固体潮形变特征,选取O1潮波作为代表,用谱-有限元法计算2~4阶无量纲径向位移U、横向位移V与力位Φ1随半径变化的数值解,结果见图 3。图 3表明,U与V在内核里几乎为0并且变化极小;在液核里,由于μ=0,只能得到U与V的线性关系式,导致两者空缺;在地幔中,U变化平缓,V缓慢下降;Φ1在地心为0,随着半径增加而持续增大,且增速在近地表达到最大。通过比较可知,图 3所示的基于PREM地球模型谱-有限元法数值解呈现的地球内部固体潮形变径向变化特征与图 1中的同质地球模型的解析解基本一致,尽管无法像徐建桥等[16]用传统4阶Runge-Kutta法获得液核中的横向位移与径向位移,但谱-有限元法获得的地球内部固体潮形变径向数值解足够平滑,在物理意义上解的连续性较好,因此该方法对液核作中性分层流体近似是确切可行的。
|
图 3 O1潮波无量纲径向位移U、横向位移V与力位Φ1随半径变化 Fig. 3 The variation of dimensionless radial displacement U, transversal displacement V and gravitational potential perturbation Φ1 in O1 frequency over the radius |
为了研究传统4阶Runge-Kutta法相较于谱-有限元法计算低阶体潮Love数数值的差异,选择O1、M2与M3潮波分别作为周日波、半日波与1/3日波的代表,用谱-有限元法计算低阶体潮Love数,并与传统4阶Runge-Kutta法的数值结果比较(表 2)。表 2中,同一潮波有上下两行计算结果,上行为用徐建桥等[16]4阶Runge-Kutta法的计算结果,下行为本文计算结果。对比分析表明,2种方法总的平均差异为1.4×10-4,频率依赖性极其微小。主要差异来源于2阶与3阶体潮Love数,差异约为2.3×10-4;在3阶O1波差异最大,约为4.3×10-4;4阶体潮Love数差异较小,在10-5量级。考虑到目前固体潮的观测精度处于10-4~10-5量级[12-13],并且目前已探明对于洲际性地球内部密度的变化可导致体潮Love数10-3量级的增量[17],2种方法在计算低阶体潮Love数的差异是不可忽略的。综上,谱-有限元法在1 km等间距剖分时的精度可达10-8量级,而Runge-Kutta法的结果目前没有进行过精度评定,因此前者较后者在精度评定方面具有优势,为其应用提供了精度依据。
|
|
表 2 4阶Runge-Kutta法与谱-有限元方法数值计算的体潮Love数 Tab. 2 The tide Love numbers results obtained from the 4th Runge-Kutta method and finite element method |
利用实测重力潮汐因子检验谱-有限元法数值计算结果的有效性。n阶理论重力潮汐因子δn可以根据式(17)求得:
| $ {\rm{}}{\delta _n} = 1 + \frac{2}{n}{h_n} - \frac{{n + 1}}{n}{k_n} $ | (17) |
式中,hn与kn为数值计算得到的第n阶Love数。根据式(17)和本研究用谱-有限元法基于PREM地球模型计算的2~5阶Love数(hn和kn)理论值,可计算得到2~5阶的重力潮汐因子分别为:δ2(M2)=1.156 88,δ3(M3)=1.069 54,δ4(M4)=1.036 01,δ5(M5)=1.022 80。可以看出,重力潮汐因子理论值随着阶数的增加,其值逐渐减小,最终趋近于1。观测重力潮汐因子选择Sun等[18]给出的8个主潮波的重力潮汐因子,这些重力潮汐因子经过了NA099海潮模型海潮负荷改正,是用Eterna潮汐调和程序分析获得的,所用数据为武汉、丽江与拉萨台超导重力仪2 a连续预处理后观测数据。谱-有限元法计算的重力潮汐因子理论值与3个台站的观测值的比较见表 3。
|
|
表 3 观测重力潮汐因子与理论值的比较 Tab. 3 Gravimetric factors obtained from gravity observation and theory calculation |
表 3中的数值结果表明,3个台站的重力潮汐理论值与观测值在P1与K1潮波的差异均较大,差值分别约为-0.5%与-1.6%,这是由于P1与K1潮波频率与液核的近周日自由摆动(NDFW)频率相近,重力潮汐因子的观测值会受其共振的影响。除了P1与K1潮波以外,其他潮波理论重力潮汐因子与丽江、拉萨台观测重力潮汐因子相差分别约为0.35%、0.35%,与武汉台观测重力潮汐因子相差约为0.15%。可以看出,理论重力潮汐因子与武汉台观测值偏差较小,而与拉萨和丽江台观测值偏大,引起这种差别最有可能的原因是地壳厚度的横向不均匀。3个台站几乎在同一纬度圈,但拉萨台海拔约为3.6 km,地壳厚度约为70 km;丽江台海拔约为2.4 km,地壳厚度约为50 km;而武汉台海拔约为0.1 km,地壳厚度约为35 km,3个台站海拔和地壳厚度差别非常大。另一方面,计算理论重力潮汐因子所用的PREM地球模型的地壳厚度约为33 km,与拉萨和丽江台的地壳厚度差别较大,与武汉台的地壳厚度相近,因此观测重力潮汐因子与理论值的差别最小,更能反映PREM地球模型下的固体潮形变响应。3个台站观测值与理论值的比较结果极有力地验证了本研究用谱-有限元法计算固体潮形变的准确性。
3 结语本研究用固体介质的哈密顿变分原理与静态中性分层的液态内核假设,导出了体潮问题的弱解形式,并用Galerkin方法进行空间离散化,将解函数与试探函数在球面上进行球谐展开,在径向上采用线性函数内插,利用SNERI地球模型不同阶次球谐展开完全解耦的特性,获得一个包含解矢量的线性对角稀疏系统,最后进行2~10阶Love数的数值计算。
数值计算表明,以同质地球模型的解析解结果作为参考,谱-有限元法计算的地表Love数随径向剖分每细化10倍,计算精度提高约2个数量级。在1 km径向等间距剖分时,数值解的精度在10-8量级;在0.1 km径向等间距剖分时,数值解的精度可达10-9量级,表明了谱-有限元方法在体潮问题上良好的收敛性与计算精度。考虑到目前固体潮观测的精度与计算机数值计算的耗时,本研究推荐1 km等间距剖分。研究结果还表明,PREM地球模型地球内部形变谱-有限元法计算结果有较强的物理连续性,液核的中性分层近似是确切可行的。将PREM地球模型Love数谱-有限元法计算结果与传统4阶Runge-Kutta法计算结果相比,可以发现,2~3阶Love数平均差异约为2.3×10-4,在高精度的体潮Love数计算中如此大的差异是不可忽视的。与武汉、拉萨和丽江台超导重力仪观测重力潮汐因子相比,PREM地球模型理论重力潮汐因子在武汉台偏差最小(0.15%),有力验证了本研究用谱-有限元法计算固体潮形变的准确性。但在液核中采用静态中性分层假设,弱化了潮汐运动频率对液核形变的影响,这是本方法下一步需要改进的地方。
| [1] |
许厚泽, 徐建桥, 孙和平, 等. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010 (Xu Houze, Xu Jianqiao, Sun Heping, et al. Solid Earth Tide[M]. Wuhan: Hubei Science and Technology Press, 2010)
(  0) 0) |
| [2] |
Hartmann T, Wenzel H. The HW95 Tidal Potential Catalogue[J]. Geophysical Research Letters, 1995, 22(24): 3553-3556 DOI:10.1029/95GL03324
(  0) 0) |
| [3] |
Lau H C P, Mitrovica J X, Davis J L, et al. Tidal Tomography Constrains Earth's Deep-Mantle Buoyancy[J]. Nature, 2017, 551(7 680): 321-326
(  0) 0) |
| [4] |
周江存, 徐建桥, 孙和平. 中国大陆精密重力潮汐改正模型[J]. 地球物理学报, 2009, 52(6): 1474-1482 (Zhou Jiangcun, Xu Jianqiao, Sun Heping. Accurate Correction Models for Tidal Gravity in Chinese Continent[J]. Chinese Journal of Geophysics, 2009, 52(6): 1474-1482 DOI:10.3969/j.issn.0001-5733.2009.06.008)
(  0) 0) |
| [5] |
Dahlen F A, Tromp J. Theoretical Global Seismology[M]. Princeton: Princeton University Press, 1998
(  0) 0) |
| [6] |
Martinec Z. Spectral-Finite Element Approach to Three-Dimensional Viscoelastic Relaxation in a Soherical Earth[J]. Geophys J Int, 2000, 142(1): 117-141 DOI:10.1046/j.1365-246x.2000.00138.x
(  0) 0) |
| [7] |
Tanaka Y Y, Klemann V, Martinec Z, et al. Spectral-Finite Element Approach to Viscoelastic Relaxation in a Spherical Compressible Earth: Application to GIA Modelling[J]. Geophyscial Journal International, 2011, 184(1): 220-234 DOI:10.1111/j.1365-246X.2010.04854.x
(  0) 0) |
| [8] |
廖彬彬, 徐建桥, 孙和平, 等. 利用谱元法计算SNREI地球的表面负荷变形[J]. 地球物理学报, 2019, 62(7): 2382-2393 (Liao Binbin, Xu Jianqiao, Sun Heping, et al. Spectral Element Method Approach to Load Deformation in a SNREI Earth[J]. Chinese Journal of Geophysics, 2019, 62(7): 2382-2393)
(  0) 0) |
| [9] |
Wu P, Peltier W R. Viscous Gravitational Relaxation[J]. Geophysical Journal of the Royal Astronomical Society, 1982, 70(2): 435-485 DOI:10.1111/j.1365-246X.1982.tb04976.x
(  0) 0) |
| [10] |
Agnew D C. 3.06-Earth Tides[J]. Treatise on Geophysics, 2007, 163-195
(  0) 0) |
| [11] |
Yuan L G, Chao B F, Ding X L, et al. The Tidal Displacement Field at Earth's Surface Determined Using Global GPS Observations[J]. Journal of Geophysical Research Solid Earth, 2013, 118(5): 2618-2632 DOI:10.1002/jgrb.50159
(  0) 0) |
| [12] |
Xu J Q, Sun H P, Ducarme B. A Global Experimental Model for Gravity Tides of the Earth[J]. Journal of Geodynamics, 2004, 38(3-5): 293-306 DOI:10.1016/j.jog.2004.07.003
(  0) 0) |
| [13] |
Sun H P, Hsu H T, Jentzsch G, et al. Tidal Gravity Observations Obtained with a Superconducting Gravimeter at Wuhan/China and Its Application to Geodynamics[J]. Journal of Geodynamics, 2002, 33(1-2): 187-198 DOI:10.1016/S0264-3707(01)00063-1
(  0) 0) |
| [14] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth and Planetary Interiors, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [15] |
汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷Love数数值计算的新进展[J]. 地球物理学报, 1996, 39(增1): 182-189 (Wang Hansheng, Xu Houze, Li Guoying. Improvement of Computations of Load Love Numbers of SNERI Earth Model[J]. Chinese Journal of Geophysics, 1996, 39(S1): 182-189)
(  0) 0) |
| [16] |
徐建桥, 孙和平. SNREI地球对表面负荷和引潮力的形变响应[J]. 地球物理学报, 2003, 46(3): 328-334 (Xu Jianqiao, Sun Heping. Deformation Response of a SNREI Earth to Surface Loads and Tidal Forces[J]. Chinese Journal of Geophysics, 2003, 46(3): 328-334 DOI:10.3321/j.issn:0001-5733.2003.03.008)
(  0) 0) |
| [17] |
Lau H C P, Mitrovica J X, Davis J L, et al. Tidal Tomography Constrains Earth's Deep-Mantle Buoyancy[J]. Nature, 2017, 551(7 680): 321-326
(  0) 0) |
| [18] |
Sun H P, Zhang H K, Xu J Q, et al. Influences of the Tibetan Plateau on Tidal Gravity Detected by Using SGs at Lhasa, Lijiang and Wuhan Stations in China[J]. Terrestrial Atmospheric and Oceanic Sciences, 2019, 30(1): 139-149 DOI:10.3319/TAO.2019.02.14.01
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40

