2. 现代工程测量国家测绘地理信息局重点实验室,上海市四平路1239号,200092
现代测绘数据采集的特点包括数据量大、种类繁多等,因此在观测数据中难免会出现粗差。目前粗差探测与识别方法主要有两类:一类将粗差纳入随机模型,认为粗差与正常观测值等期望,但方差变大,由此发展了抗差估计理论[1]。还有一类将粗差纳入函数模型,认为粗差导致该观测值期望变化,由此发展了数据探测法[2]。施闯等[3]提出基于相关分析进行粗差定位,后来不断扩充到由偏相关系数和复相关系数进行多维粗差定位。关于粗差定位与定值,欧吉坤[4]提出拟准检定法(QUAD法)。於宗俦等[5]提出LEGE方法进行多维粗差的探测和估计;林国庆等[6]提出利用部分最小二乘(PLS)用于多维粗差的定位与定值。笔者提出一种新的确定粗差大小的方法,即先验方差待定参数法PVUP(prior-variance undecided parameter method),其在先验方差准确时可确定粗差的大小。
1 基本原理与数学模型 1.1 基本原理假设有一组不包含粗差的观测数据{L1, L2, L3, L4…Ln-1, Ln},其对应的误差方程为:
| $ \underset{n\times 1}{\mathop{\boldsymbol{v}}}\,=\underset{n\times t}{\mathop{\boldsymbol{A}}}\,\underset{t\times 1}{\mathop{\boldsymbol{x}}}\,-{{\left[ {{L}_{1}}\ \ \ldots \ \ {{L}_{n}} \right]}^{\text{T}}} $ | (1) |
这时假定L1观测值含有粗差。去掉L1观测值得到新的误差方程:
| $ \underset{(n\text{-1})\times 1}{\mathop{{\boldsymbol{{v}'}}}}\,=\underset{(n-1)\times t}{\mathop{{\boldsymbol{{A}'}}}}\,\underset{t\times 1}{\mathop{\boldsymbol{x}}}\,-{{\left[ \begin{matrix} {{L}_{2}}\ \ \ldots \ \ {{L}_{n}} \\ \end{matrix} \right]}^{\text{T}}} $ | (2) |
根据式(2)可计算单位权方差
| $ \underset{n\times 1}{\mathop{\boldsymbol{v}}}\,=\underset{n\times t}{\mathop{\boldsymbol{A}}}\,\underset{t\times 1}{\mathop{\boldsymbol{x}}}\,-{{[\begin{matrix} y\ \ \ldots \ \ {{L}_{n}} \\ \end{matrix}]}^{\text{T}}} $ | (3) |
计算式(3)的单位权方差
先验方差待定参数法需要确定先验方差。可以从3种方法获取先验方差信息:1)根据拟准观测值[4]进行计算(如何选取拟准观测值参考文献[7]);2)根据仪器的观测精度和观测值的先验噪声大小确定;3)根据已知稳固的数据(历史数据)确定。
假设已经将观测数据正确地分成两类:1)不含粗差的数据;2)可能含有粗差待确定的数据。假设根据剔除所有怀疑含有粗差的数据计算出的单位权方差
假设第1类观测值向量为L, 对应的系数矩阵为A′,根据最小二乘计算出的单位权方差为
根据AX = L + Δ可以得到误差方程:
| $ \mathit{\boldsymbol{V'}} = \mathit{\boldsymbol{A'X}} - \mathit{\boldsymbol{L}} $ | (4) |
并根据
| $ \mathit{\boldsymbol{L'}} = {[\begin{array}{*{20}{c}} y&{{\mathit{\boldsymbol{L}}^{\rm{T}}}} \end{array}]^{\rm{T}}} $ | (5) |
则式(4)变成:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{L'}} $ | (6) |
根据最小二乘原理可得参数X的估值:
| $ \mathit{\boldsymbol{X}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L'}} $ | (7) |
令
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{JL'}} $ | (8) |
将式(8)代入式(6)得:
| $ {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} = {{\rm{(}}\mathit{\boldsymbol{L'}}{\rm{)}}^{\rm{T}}}{\rm{(}}\mathit{\boldsymbol{E}} - \mathit{\boldsymbol{AJ}}{\rm{)}}\mathit{\boldsymbol{L'}} $ | (9) |
其中E为单位矩阵。再令M = E - AJ得:
| $ {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} = {(\mathit{\boldsymbol{L'}})^{\rm{T}}}\mathit{\boldsymbol{ML'}} $ | (10) |
将M进行分块:
| $ \mathit{\boldsymbol{M}} = \left( \begin{array}{l} \mathop {{\mathit{\boldsymbol{M}}_{11}}}\limits_{1 \times 1} \\ \mathop {{\mathit{\boldsymbol{M}}_{21}}}\limits_{(n - 1) \times 1} \end{array} \right.\left. \begin{array}{l} \mathop {{\mathit{\boldsymbol{M}}_{12}}}\limits_{1 \times (n - 1)} \\ \mathop {{\mathit{\boldsymbol{M}}_{22}}}\limits_{(n - 1) \times (n - 1)} \end{array} \right) $ | (11) |
其中, n为A的行数, 也即式(7)中的观测值数。将式(5)、(11)代入式(10)得:
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{M}}_{11}}{y^2} + ({\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_{21}} + {\mathit{\boldsymbol{M}}_{12}}\mathit{\boldsymbol{L}})y + \\ {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_{22}}\mathit{\boldsymbol{L}} = (n - m)\hat \sigma _{\rm{0}}^{\rm{2}} \end{array} $ | (12) |
式中最右端已经计算出来,为已知值。令
| $ \left\{ \begin{array}{l} a = {\mathit{\boldsymbol{M}}_{11}}\\ b = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_{21}} + {\mathit{\boldsymbol{M}}_{12}}\mathit{\boldsymbol{L}}\\ c = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_{22}}\mathit{\boldsymbol{L}} - (n - m)\hat \sigma _0^2 \end{array} \right. $ |
可将(12)式化为一元二次方程。解此一元二次方程,便得到y的值,即Ln。Ln减去实际观测值便得到精确的粗差大小。这里需说明3个问题:1)该方法是直接确定观测值应有值。不难发现,如果计算得到应有值与实际相差很大,可以肯定该观测值确有粗差;相反,若相差不大,则之前分类可能出现问题或者该观测值并不含粗差。2)该一元二次方程有2个值,具体选取哪一个值可以根据观测值的合理性选取或根据其他粗差估计方式获得的值当作初值进行选取。3)这里待定参数的估值y其实质是根据不含粗差观测值的精度求得的,即根据应有的观测精度去推求含有粗差的观测值应有值,其精度自然与不含粗差的观测值精度一致,从而达到准确探测粗差大小的目的。
2 算例分析算例1 取文献[8]的水准网,网形及相应观测值如图 1(单位m)所示。分别在l1观测值模拟3 m、4 m、5 m、10 m粗差,且假设观测值等权独立。由文献[8]知,当观测值等权独立时,数据探测法、PLS法、QUAD法以及LEGE法是等价的,故利用本文提出的先验方差待定参数法估计l1上的粗差,并与上述4种方法进行对比(表 1)。从表 1可以看出,当观测值独立等权的时候,先验方差待定参数法能够和其他4种方法达到同样的效果。但其先验方差待定参数并不与上述方法等价(参见算例2),其具体的证明方法还需要进一步的研究。但是可以确定的是,先验方差精度越高,PVUP法越适用。
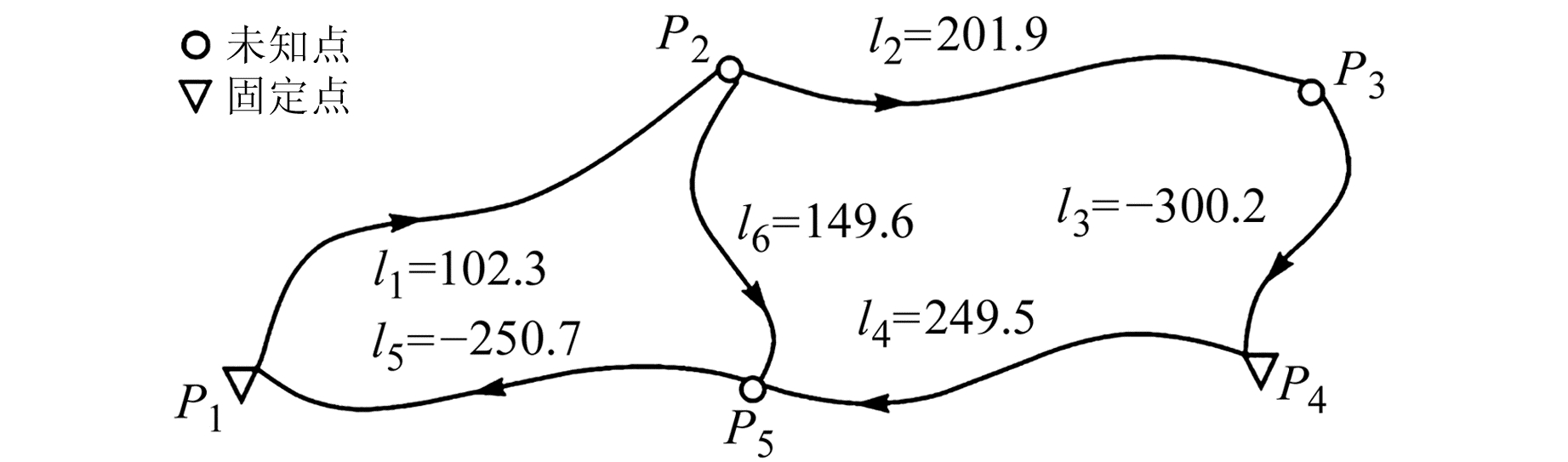
|
图 1 水准网 Fig. 1 Leveling network |
|
|
表 1 不同粗差估值结果比较 Tab. 1 Comparisons of gross estimation of different methods |
算例2 采用文献[4]中的测角网,用先验方差待定参数法求得的粗差估值与拟准检定进行对比(因为有学者已经证明观测值等权独立时,数据探测法、PLS法、QUAD法以及LEGE法是等价的,下文仅与QUAD法比较)。从表 2可以看出,本文的先验待定参数法与QUAD法并不等价,且优于QUAD法估计的粗差精度。
|
|
表 2 拟准法与先验方差待定参数估计粗差精度对比 Tab. 2 Comparison of gross estimation using QUAD and PVUP |
算例3 给出先验待定参数法在周跳探测里的应用。含有周跳的GPS观测值显然是一种粗差。现有原始相位观测值和含模拟周跳的相位观测值如表 3,并在第35号观测值加入10周周跳。接下来说明先验方差待定参数方法在周跳探测中的运用。根据前5个相位观测数据计算单位权方差(可利用多项式拟合法计算该方差),该算例的单位权方差为
|
|
表 3 原始相位观测值和含模拟周跳的相位观测值 Tab. 3 Raw carrier-phase and simulated-cycle carrier-phase observation |
本文提出一种新的粗差估计方式——先验方差待定参数法,其在先验方差准确时可达到确定粗差大小的目的。待定参数法也可以与其他粗差探测方法结合,不局限于拟准观测,且不一定要准确探测出粗差位置,也可估计粗差估值(如算例3)。准确确定粗差值,可以提高数据利用率,同时其准确性也能用于数据质量评估等。但该方法仅考虑同精度独立观测值的情况,不同精度或者相关观测值的适用性还需进一步研究。
| [1] |
周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 12(2): 115-120 (Zhou Jiangwen. Classical Theory Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 12(2): 115-120 DOI:10.3321/j.issn:1001-1595.1989.02.005)
(  0) 0) |
| [2] |
Baarda W. A Testing Procedure for Use in Geodetic Networks[J]. Netherland and Geodetic Commission, 1968, 2(5)
(  0) 0) |
| [3] |
施闯, 刘经南. 基于相关分析的粗差理论[J]. 武汉测绘科技大学学报, 1998, 23(1): 5-9 (Shi Chuang, Liu Jingnan. Correspondence Based Outlier Analysis[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 5-9 DOI:10.3321/j.issn:1671-8860.1998.01.002)
(  0) 0) |
| [4] |
欧吉坤. 一种检测粗差的新方法——拟准检定法[J]. 科学通报, 1999, 44(16): 1777-1781 (Ou Jikun. Quasi-Accurate Detection of Gross Errors(QUAD)[J]. Chinese Science Bulletin, 1999, 44(16): 1777-1781 DOI:10.3321/j.issn:0023-074X.1999.16.021)
(  0) 0) |
| [5] |
於宗俦, 李明峰. 多维粗差的同时定位与定值[J]. 武汉测绘科技大学学报, 1996, 21(4): 323-329 (Yu Zongchou, Li Mingfeng. Simultaneous Location and Evaluation of Multidimensional Gross Errors[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(4): 323-329)
(  0) 0) |
| [6] |
林国庆, 范东明, 谢用, 等. 部分最小二乘平差的快速多维粗差定位定值法[J]. 测绘, 2010, 33(4): 162-164 (Lin Guoqing, Fan Dongming, Xie Yong, et al. Method of Partly Least Squares in Fast Gross Error Location and Estimation[J]. Surveying and Mapping, 2010, 33(4): 162-164)
(  0) 0) |
| [7] |
柴艳菊, 欧吉坤, 袁运斌, 等. 粗差拟准检定的实施方案设计[J]. 测绘工程, 2001, 10(1): 19-22 (Chai Yanju, Ou Jikun, Yuan Yunbin, et al. Scheme Design of Quasi-Accurate Detection of Gross Errors[J]. Engineering of Surveying and Mapping, 2001, 10(1): 19-22 DOI:10.3969/j.issn.1006-7949.2001.01.005)
(  0) 0) |
| [8] |
鲁铁定. 几种粗差估值方法的比较[J]. 测绘学报, 2016, 45(6): 656-662 (Lu Tieding. Comparison of Several Methods for Outlier Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 656-662)
(  0) 0) |
2. Key Laboratory of Modern Engineering Surveying of NAMSG, 1239 Siping Road, Shanghai 200092, China
 2020, Vol. 40
2020, Vol. 40


