测绘数据处理模型常常呈现病态性，此时观测值微小的扰动会导致解严重偏离真值，因此常规的最小二乘解极不可靠。为获得稳定、可靠的参数估值，学者们提出一系列有偏估计，通过牺牲解的无偏性来换取有效性。常用的有偏估计包括截断奇异值分解(truncated singular value decomposition, TSVD)、Tikhonov正则化以及Liu估计等。模型的病态性主要体现在系数阵小奇异值对参数估值及其方差的放大上。截断奇异值法的基本思想是将小的奇异值截掉使得法矩阵求逆变得稳定从而获得可靠的参数估值，但其只适用于处理奇异值突变的情形。Tikhonov正则化法在最小二乘准则基础上对参数引入稳定泛函约束，并通过正则化参数调节两者的平衡，当稳定泛函取参数的二次范数时，正则化法退化为岭估计。正则化法的研究多集中于正则化参数的选取^[1]以及正则化矩阵的构造^[2]。从正则化解的谱分解式^[3]来看，正则化法利用正则化参数修正奇异值以削弱小奇异值对参数估值的影响，然而其不加区别地对所有奇异值进行修正显然是不合理的。邓凯亮等^[4]在处理向下延拓航空重力数据时，将系数阵奇异值分为可靠部分和不可靠部分，提出一种双参数修正法，并利用GCV法确定截断参数和正则化参数；郭杰等^[5]利用复共线性进行诊断和度量，确定参数估值受复共线性危害的程度和部位，并对解进行偏差改正; 林东方等^[6]通过比较正则化解方差下降量与偏差引入量，提出一种改进的岭估计解法。由于改进后的正则化法仍然破坏了线性观测模型的结构，故其解和残差是有偏的，利用有偏残差估计得到的单位权中误差也是有偏的。沈云中等^[7]和张俊等^[8]利用残差二次型的数学期望公式分别导出正则化解和半参数模型补偿最小二乘解的单位权中误差无偏估计式；Xu等^[9]导出病态模型的无偏方差分量估计式。本文根据同样的思路，利用改进正则化解的残差导出其无偏的单位权中误差估计式，然后用数值算例和病态测边网算例验证算法的有效性。

1 G-M模型的最小二乘解及其谱分解式

常用的G-M模型为：

${\boldsymbol{L}} = {\boldsymbol{AX}}{\rm{ + }}{\boldsymbol{e}}$

(1)

式中, L ∈ R^m为观测向量, e ∈ R为误差向量, A ∈ R^m×n为系数阵(满足rank(A)=n < m), X ∈ Rⁿ为未知参数。其随机模型为：

$\begin{array}{l}\left\{ \begin{array}{l} E({\boldsymbol{e}}) = 0\\ D({\boldsymbol{e}}) = \sigma _0^2{{\boldsymbol{P}}^{ - 1}}\end{array} \right. \end{array}$

(2)

式中, σ₀为单位权中误差, P为观测值的权阵。在最小二乘准则下：

${{\boldsymbol{e}}^T}{\boldsymbol{Pe}} = \min $

(3)

可得参数的最小二乘估值及其方差为：

$ \begin{array}{l}\left\{ \begin{array}{l} {{{\boldsymbol{\hat X}}}_L} = {({{\boldsymbol{A}}^T}{\boldsymbol{PA}})^{ - 1}}({{\boldsymbol{A}}^T}{\boldsymbol{PL}})\\ {{\boldsymbol{D}}_L} = \sigma _0^2{({{\boldsymbol{A}}^T}{\boldsymbol{PA}})^{ - 1}}\end{array} \right. \end{array} $

(4)

在式(1)等号两边同时乘以权阵的平方根分解矩阵得：

${\boldsymbol{\bar L}} = {\boldsymbol{\bar AX}} + {\boldsymbol{\bar e}}$

(5)

式中，$\overline{\boldsymbol{L}}=\sqrt{\boldsymbol{P}} \boldsymbol{L}, \overline{\boldsymbol{A}}=\sqrt{\boldsymbol{P}} \boldsymbol{A}, \bar{e}=\sqrt{\boldsymbol{P}} e$, 显然新的观测值$\overline{\boldsymbol{L}}$的方差为：

$\begin{array}{l} {{\boldsymbol{D}}_{{{\bar L}}}} = {{\boldsymbol{D}}_{{{\bar e}}}} = \sqrt {\boldsymbol{P}} {{\boldsymbol{D}}_{{e}}}\sqrt {\boldsymbol{P}} = \sigma _0^2\sqrt {\boldsymbol{P}} {{\boldsymbol{P}}^{ - 1}}\sqrt {\boldsymbol{P}} = \sigma _0^2{{\boldsymbol{I}}_m} \end{array}$

(6)

式中, I为单位阵。即不等权模型(1)在模型两边同乘权阵的平方根，分解矩阵可变成等权模型(式(5))。为推导方便，假设权阵P为单位阵。将A进行奇异值分解：

$ {\boldsymbol{A}} = {\boldsymbol{U\Sigma }}{{\boldsymbol{V}}^T} = \sum\limits_{i = 1}^n {{\lambda _i}{{\boldsymbol{u}}_i}} {\boldsymbol{v}}_i^T $

(7)

式中，U ∈ R^m×m, V ∈ R^n×n均为正交阵, Σ = $\left[\begin{array}{l}\boldsymbol{D} \\ 0\end{array}\right] \in \boldsymbol{R}^{m \times n}$，D为n阶对角阵，其对角元为系数阵的奇异值。将式(7)代入式(4)可得最小二乘解及其方差的谱分解式^[9]：

$ \begin{array}{l}\left\{ \begin{array}{l} {{{\boldsymbol{\hat X}}}_L} = \sum\limits_{i = 1}^n {\frac{{{{\boldsymbol{v}}_i}{\boldsymbol{u}}_i^T}}{{{\lambda _i}}}} {\boldsymbol{L}}\\ {{\boldsymbol{D}}_L} = \sigma _{\rm{0}}^{\rm{2}}\sum\limits_{i = 1}^n {\frac{{{{\boldsymbol{v}}_i}{\boldsymbol{v}}_i^T}}{{\lambda _i^2}}} \end{array} \right. \end{array} $

(8)

2 病态模型的改进正则化解及其单位权中误差无偏估计 2.1 改进正则化解

当系数阵病态时，其奇异值单调趋于0。由式(8)可知，模型的病态性主要体现在小奇异值对参数估值及其方差的放大上，导致最小二乘解极不可靠。为获得稳定的参数估值，需采用正则化方法削弱系数阵的病态性。常用的正则化方法为Tikhonov正则化法^[10]，其基本准则为：

$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {{\boldsymbol{e}}^T}{\boldsymbol{e}} + \alpha {{\boldsymbol{X}}^T}{\boldsymbol{RX}} = \min $

(9)

式中, α为正则化参数, R为正则化矩阵，一般取单位阵。则参数的正则化解为：

$\begin{array}{l} {{{\boldsymbol{\hat X}}}_R} = {({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {{\boldsymbol{I}}_n})^{ - 1}}({{\boldsymbol{A}}^T}{\boldsymbol{L}})=\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^n {\frac{{{\lambda _i}}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{v}}_i}} {\boldsymbol{v}}_i^T{\boldsymbol{L}} \end{array}$

(10)

其偏差、方差以及均方误差为：

$\begin{array}{l}\left\{ \begin{array}{l} {\rm{bias}}({{{\boldsymbol{\hat X}}}_R}) = E({{{\boldsymbol{\hat X}}}_R}) - {\boldsymbol{X}} = - \alpha {({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}{\boldsymbol{X}}\\ D({{{\boldsymbol{\hat X}}}_R}) = \sigma _0^2{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}\\ {\rm{MSE}}({{{\boldsymbol{\hat X}}}_R}) = D({{{\boldsymbol{\hat X}}}_R}) + {\rm{bias}}({{{\boldsymbol{\hat X}}}_R}){\rm{bias}}{^T}({{{\boldsymbol{\hat X}}}_R}) =\\ \sigma _0^2{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}} + \\{\alpha ^{\rm{2}}}{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}{\boldsymbol{X}}{{\boldsymbol{X}}^T}{({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {\boldsymbol{I}})^{ - 1}}\end{array} \right. \end{array}$

(11)

考虑到均方误差的迹表征参数的总体方差，将式(7)代入MSE($\hat{\boldsymbol{X}}_{R}$)，并求迹得：

$ {\rm{tr}}({\rm{MSE}}({{\boldsymbol{\hat X}}_R})) = \sum\limits_{i = 1}^n {\frac{{\sigma _{\rm{0}}^{\rm{2}}\lambda _i^2{\rm{ + }}{\alpha ^2}{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2}}}{{{{(\lambda _i^2 + \alpha )}^2}}}} $

(12)

最小二乘解方差阵的迹为：

${\rm{tr}}({{\boldsymbol{D}}_L}) = \sum\limits_{i = 1}^n {\frac{{\sigma _{\rm{0}}^{\rm{2}}}}{{\lambda _i^2}}} $

(13)

比较式(13)与式(12)，只有当$\sigma_{0}^{2} / \lambda_{i}^{2}>\left(\boldsymbol{v}_{i}^{\mathrm{T}} \boldsymbol{X}\right)^{2}$时^[6]，修正i所对应的奇异值才能有效降低估值的均方误差。考虑到σ₀²/λ_i²随奇异值的减小而逐渐增大，当增大至超过${\left({\mathit{\boldsymbol{v}}_i^{\rm{T}}\mathit{\boldsymbol{X}}} \right)^2}$时，可判定该处及之后的奇异值需修正，由此确定截断参数。假设后n－k个奇异值需修正，则改进后的正则化解为^[6]：

$\begin{array}{l} {{{\boldsymbol{\hat X}}}_{\rm CD}} = {({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T)^{ - 1}}({{\boldsymbol{A}}^T}{\boldsymbol{L}}) =\\ \sum\limits_{i = 1}^k {\frac{1}{{{\lambda _i}}}{{\boldsymbol{v}}_i}} {\boldsymbol{v}}_i^T{\boldsymbol{L}} + \sum\limits_{i = k + 1}^n {\frac{{{\lambda _i}}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{v}}_i}} {\boldsymbol{v}}_i^T{\boldsymbol{L}} \end{array}$

(14)

式中，V₁为V的第k+1~n列向量构成的矩阵。

2.2 单位权中误差无偏估计

记Q_CR=(A^TA +αV₁V₁^T)^－1, 将式(14)代入式(1)，可得改进正则化解的残差：

$\begin{array}{l} {{{\boldsymbol{\hat e}}}_{\rm{CR}}} = {\boldsymbol{L}} - {\boldsymbol{A}}{{{\boldsymbol{\hat X}}}_{\rm{CR}}} = ({{\boldsymbol{I}}_m} - {\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}){\boldsymbol{L}} \end{array}$

(15)

为推导方便，先给出如下辅助关系式：

$\begin{array}{l} {{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}{\boldsymbol{A}} = {({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T)^{ - 1}}({{\boldsymbol{A}}^T}{\boldsymbol{A}} + \alpha {{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T - \\ \alpha {{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T) = {{\boldsymbol{I}}_n} - \alpha {{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T \end{array}$

(16)

残差的数学期望为：

$\begin{array}{l} E({{{\boldsymbol{\hat e}}}_{\rm{CR}}}) = ({{\boldsymbol{I}}_m} - {\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}){\boldsymbol{AX}} = \alpha {\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{\boldsymbol{X}} \end{array}$

(17)

将式(7)代入式(17)并略作推导，可得$E\left(\hat{\boldsymbol{e}}_{\mathrm{CR}}\right)$的谱分解式：

$\begin{array}{l} E({{{\boldsymbol{\hat e}}}_{\rm{CR}}}) = \alpha \sum\limits_{i = 1}^n {{\lambda _i}{{\boldsymbol{u}}_i}{\boldsymbol{v}}_i^T} \cdot (\sum\limits_{i = 1}^k {\frac{{{{\boldsymbol{v}}_i}{\boldsymbol{v}}_i^T}}{{\lambda _i^2}} + \sum\limits_{i = k + 1}^n {\frac{{{{\boldsymbol{v}}_i}{\boldsymbol{v}}_i^T}}{{\lambda _i^2 + \alpha }}} } ) \cdot \\ \sum\limits_{i = k + 1}^n {{{\boldsymbol{v}}_i}{\boldsymbol{v}}_i^T} {\boldsymbol{X}} = \alpha \sum\limits_{i = k + 1}^n {\frac{{{\lambda _i}}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{u}}_i}} {\boldsymbol{v}}_i^T{\boldsymbol{X}} \end{array}$

(18)

则$E\left(\hat{\boldsymbol{e}}_{\mathrm{CR}}\right)$的二次型为：

$ \begin{array}{l} {E^T}({{{\boldsymbol{\hat e}}}_{\rm{CR}}})E({{{\boldsymbol{\hat e}}}_{\rm{CR}}}) = {\alpha ^2}{{\boldsymbol{X}}^T}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{{\boldsymbol{Q}}_m}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{{\boldsymbol{Q}}_m}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{\boldsymbol{X}}=\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \sum\limits_{i = k + 1}^n {\frac{{{\lambda _i}}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{X}}^T}{{\boldsymbol{v}}_i}} {\boldsymbol{u}}_i^T \cdot \alpha \sum\limits_{i = k + 1}^n {\frac{{{\lambda _i}}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{u}}_i}} {\boldsymbol{v}}_i^T{\boldsymbol{X}}=\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha ^2}\sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2}}}{{(\lambda _i^2 + \alpha )}}} \end{array} $

(19)

根据式(15)和误差传播定律，可得残差的方差为：

$\;\;\;\;\;\;\;\;D({{\boldsymbol{\hat e}}_{\rm{CR}}}) =\\ \sigma _0^2({\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T} - 2{\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T} + {{\boldsymbol{I}}_m})$

(20)

考虑到A的谱分解式，有：

${\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T} = \sum\limits_{i = 1}^k {{{\boldsymbol{u}}_i}{\boldsymbol{u}}_i^T} + \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2}}{{\lambda _i^2 + \alpha }}{{\boldsymbol{u}}_i}{\boldsymbol{u}}_i^T} $

(21)

将其代入式(20)可得：

$\;\;\;\;\;\;\;\;\;\;\;D({{\boldsymbol{\hat e}}_{\rm{CR}}}) =\\ \sigma _0^2({{\boldsymbol{I}}_m} - \sum\limits_{i = 1}^k {{{\boldsymbol{u}}_i}} {\boldsymbol{u}}_i^T - \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2(\lambda _i^2 + 2\alpha )}}{{{{(\lambda _i^2 + \alpha )}^2}}}{{\boldsymbol{u}}_i}{\boldsymbol{u}}_i^T} )$

(22)

则其迹为：

${\rm{tr}}(D({{\boldsymbol{\hat e}}_{\rm{CR}}})) = \sigma _{\rm{0}}^{\rm{2}}(m - k - \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2(\lambda _i^2 + 2\alpha )}}{{{{(\lambda _i^2 + \alpha )}^2}}})} $

(23)

已知二次型的期望公式为：

$E({\boldsymbol{\hat e}}_{\rm{CR}}^T{{\boldsymbol{\hat e}}_{\rm{CR}}}) = {\rm{tr}}(D({{\boldsymbol{\hat e}}_{\rm{CR}}})) + {E^T}({{\boldsymbol{\hat e}}_{\rm{CR}}})E({{\boldsymbol{\hat e}}_{\rm{CR}}})$

(24)

将式(19)和式(23)代入上式并去掉期望符号得：

${\boldsymbol{\hat e}}_{\rm{CR}}^T{{\boldsymbol{\hat e}}_{\rm{CR}}} = \sigma _{\rm{0}}^{\rm{2}}(m - k - \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2(\lambda _i^2 + 2\alpha )}}{{{{(\lambda _i^2 + \alpha )}^2}}})} {\rm{ + }}\\\;\;\;\;\;\;\;\;\;\;\;{\alpha ^2}\sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2}}}{{(\lambda _i^2 + \alpha )}}} $

(25)

则改进正则化解的无偏单位权中误差为：

${\hat \sigma _0} = \sqrt {\frac{{{\boldsymbol{\hat e}}_{\rm{CR}}^T{{{\boldsymbol{\hat e}}}_{\rm{CR}}} - {\alpha ^2}\sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2}}}{{(\lambda _i^2 + \alpha )}}} }}{{(m - k - \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2(\lambda _i^2 + 2\alpha )}}{{{{(\lambda _i^2 + \alpha )}^2}}})} }}} $

(26)

传统的单位权中误差计算公式如下：

$ {\hat \sigma _L} = \sqrt {\frac{{{\boldsymbol{\hat e}}_{CR}^T{{{\boldsymbol{\hat e}}}_{\rm{CR}}}}}{{m - n}}} $

(27)

由式(24)和式(25)可见，$E\left(\hat{\sigma}_{L}^{2}\right) \neq \sigma_{0}^{2}$，即利用传统公式求得的单位权中误差是有偏的。

2.3 正则化参数的确定

改进正则化解是有偏的，其偏差为：

$\begin{array}{l} {\rm{bias}}({{{\boldsymbol{\hat X}}}_{\rm{CR}}}) = E({{{\boldsymbol{\hat X}}}_{\rm{CR}}}) - {\boldsymbol{X}} = - \alpha {{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{\boldsymbol{X}} \end{array}$

(28)

根据式(14)和误差传播定律，可得${\mathit{\boldsymbol{\widehat X}}_{{\rm{CR}}}}$的方差为：

${\boldsymbol{D}}({{\boldsymbol{\hat X}}_{\rm{CR}}}) = \sigma _0^2{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}}$

(29)

其均方误差为：

$ \begin{array}{l} {\rm{MSE}}({{{\boldsymbol{\hat X}}}_{\rm{CR}}}) = {\boldsymbol{D}}({{{\boldsymbol{\hat X}}}_{\rm{CR}}}) + {\rm{bias}}({{{\boldsymbol{\hat X}}}_{\rm{CR}}}){\rm{bias}}{^T}({{{\boldsymbol{\hat X}}}_{\rm{CR}}})=\\ \sigma _0^2{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{A}}^T}{\boldsymbol{A}}{{\boldsymbol{Q}}_{\rm{CR}}} + {\alpha ^2}{{\boldsymbol{Q}}_{\rm{CR}}}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{\boldsymbol{X}}{{\boldsymbol{X}}^T}{{\boldsymbol{V}}_1}{\boldsymbol{V}}_1^T{{\boldsymbol{Q}}_{\rm{CR}}} \end{array} $

(30)

均方误差的迹为：

${\rm{tr}}({\rm{MSE}}({{\boldsymbol{\hat X}}_{\rm{CR}}})) = \sigma _0^2(\sum\limits_{i = 1}^k {\frac{1}{{\lambda _i^2}} + \sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2}}{{{{(\lambda _i^2 + \alpha )}^2}}}} } ) +\\\;\;\;\;\;\;\;\;\; {\alpha ^{\rm{2}}}\sum\limits_{i = k + 1}^n {\frac{{{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2}}}{{{{(\lambda _i^2 + \alpha )}^2}}}} $

(31)

式(31)是严格的凸函数，存在唯一的极小值。求式(31)对α的1阶导数并令其为0，得：

$\rho (\alpha ) = \frac{{\partial {\rm{tr}}({\rm{MSE}}({{{\boldsymbol{\hat X}}}_{\rm{CR}}}))}}{{\partial \alpha }} =\\ 2\sum\limits_{i = k + 1}^n {\frac{{\lambda _i^2(a{{({\boldsymbol{v}}_i^T{\boldsymbol{X}})}^2} - \sigma _0^2)}}{{{{(\lambda _i^2 + \alpha )}^3}}}} = 0$

(32)

式(32)是α的连续函数，可利用二分法求解。

3 算例分析 3.1 数值算例

第1类积分方程是典型的病态问题，其方程的基本形式为：

$z(y) = \int_a^b {K(x,y)f(x)dx} $

(33)

式中，K(x, y)为核函数，f(x)为原函数。本文分别取核函数和原函数为^[6]：

$\begin{array}{l}\left\{ \begin{array}{l} K(x,y) = \frac{{1.0}}{{1.0 + 100{{(y - x)}^2}}}\\ f(x) = \frac{{\exp ({\beta _1}) + \exp ({\beta _2})}}{{10.9550408}} - 0.052130913\end{array} \right. \end{array}$

(34)

式中，$\beta_{1}=-\frac{(x-0.3)^{2}}{0.03}, \beta_{2}=-\frac{(x-0.7)^{2}}{0.03}$, x∈[0, 1], y∈[－2, 2]。取采样间隔为0.02，则式(33)可离散化为：

$\;\;\;\;z({y_j}) = 0.01K({x_1},{y_j})f({x_1}) +\\ 0.02\sum\limits_{i = 2}^{50} {K({x_i}} ,{y_j})f({x_i}) + 0.01K({x_{51}},{y_j})f({x_{51}})$

(35)

将其改写为矩阵形式：

${\boldsymbol{L}} = {\boldsymbol{AX}}$

(36)

对观测值L模拟偶然误差e~N(0, σ²I)，σ₀=0.01。图 1为σ₀²/λ_i²与${\left({\mathit{\boldsymbol{v}}_i^{\rm{T}}\mathit{\boldsymbol{X}}} \right)^2}$随奇异值大小变化情况。由图可见，从第6个奇异值起，修正该处的奇异值能够有效降低均方误差。分别采用最小二乘法、正则化法和改进正则化法解算参数并计算各个估值的均方根误差：

${\rm{RMSE}} = \sqrt {\frac{{{{({\boldsymbol{\hat X}} - {\boldsymbol{X}})}^T}({\boldsymbol{\hat X}} - {\boldsymbol{X}})}}{m}} $

(37)

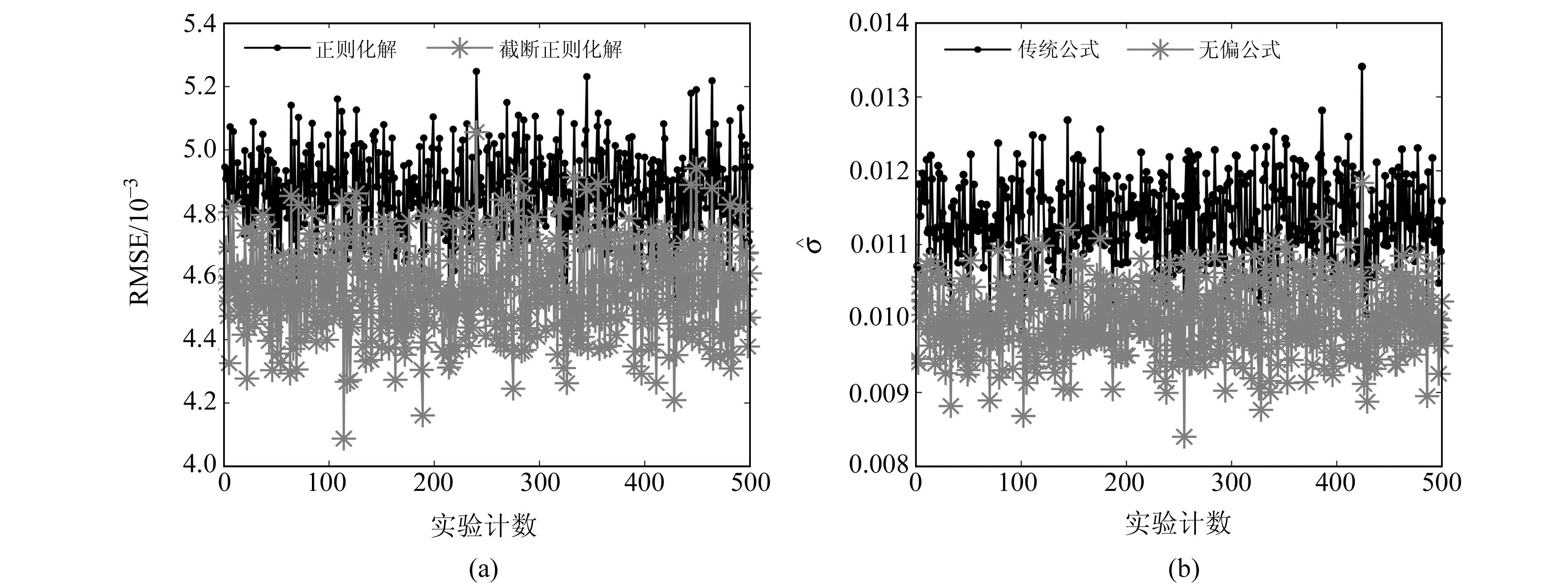
图 2为各算法的参数估值与真值的对比，其中改进正则化解的精度最高，RMSE为0.004 4；正则化解次之，RMSE为0.004 8；最小二乘解最差，RMSE为119.258 4。分别采用传统公式(27)和无偏公式(26)计算单位权中误差，结果分别为0.012 0和0.010 6，显然无偏公式计算得到的单位权中误差更接近真值。模拟500次实验，每次实验均采用同样的模拟策略，图 3(a)为500次实验的正则化解和改进正则化解的RMSE对比，正则化解的平均RMSE为0.004 9，改进正则化解的平均RMSE为0.004 5，相比正则化解提升8.16%。图 3(b)为500次实验传统公式和无偏公式算得的单位权中误差对比。显然传统公式算得的单位权中误差偏大，其均值为0.011 32，与真值相差13.20%;无偏公式算得的单位权中误差与真值较为接近, 其均值为0.009 99, 与真值相差0.1%，相比传统公式提升13.10%。

3.2 病态测边网算例

模拟一个空间测边网^[11-12]，该算例中共有11个点位A₁~A₁₁, 其中9个坐标已知(A₁~A₉)，2个坐标未知(A₁₀, A₁₁)。图 4为所有点位的二维位置分布图，表 1为已知点至未知点的距离观测值，A₁₀和A₁₁的观测距离为13.107 8 m，所有的观测值均为等精度观测，其中误差为0.001 m。A₁₀和A₁₁的坐标可根据表 1中的距离观测值确定。

同数值算例，分别采用最小二乘法、正则化法和改进正则化法解算参数估值。表 2为3种算法的估值$\mathit{\boldsymbol{\widehat X}}$及其与真值X的差值范数$\left\| {\mathit{\boldsymbol{\widehat X}} - \mathit{\boldsymbol{X}}} \right\|$。显然, 由于病态性的影响，最小二乘解的精度最低，与真值的差值范数为9.230 1;正则化解改善了法矩阵的病态性，其精度较最小二乘解大幅提高，与真值的差值范数为0.650 8;而改进正则化法仅对部分较小的奇异值进行修正，对大奇异值则不作改正，有效降低了解的均方误差，其解的精度最高，与真值的差值范数为0.572 5。分别采用传统公式和无偏公式估计单位权中误差，结果列于表 2。显然，无偏公式得到的单位权中误差更接近真值。

4 结语

由于模型病态性的影响，法矩阵的求逆变得极不稳定，病态性影响主要体现在系数阵小奇异值对参数估值及其方差的放大上，导致常规的最小二乘解极不可靠。正则化法通过引入正则化参数改善法矩阵的病态性，从正则化解的谱分解展开式来看，正则化法是通过修正奇异值来避免分母中小奇异值对解的放大。然而其不加区别地对所有奇异值进行修正显然是不合理的，尤其对于较大的奇异值，该部分解的分量相对可靠，若同样对其施加改正，则会造成解的部分失真。本文分析了正则化解和最小二乘解的均方误差的迹，通过比较其谱展开式导出确定奇异值修正与否的条件，同时利用残差二次型的期望公式导出改进正则化解的单位权中误差无偏计算公式。最后用数值算例和病态测边网算例验证了公式的正确性。