传统的点云配准方法[1]是基于离散点来实施的, 虽然取得了一定的成效, 但其配准精度易受点特征提取精度的影响[2], 由于被扫描的物体之间相互遮挡, 寻找完全对应的同名点特征十分困难。相对而言, 直线特征则具有丰富和稳定的几何特性, 广泛存在于被扫描的对象上, 即使存在遮挡情况, 也只需提取点特征所在的直线特征, 既能降低实施的复杂度, 又能保证相邻测站点云之间的高精度配准。近年来, 有学者对线特征点云配准方法进行了研究, 提出基于四元数表示的点云配准直接解法[3-4], 该方法虽无需迭代, 却不能同时求解所有的配准参数; 王永波等[5]提出一种基于Plücker直线描述的点云配准非迭代方法, 提高了配准精度; 盛庆红等[6-7]提出Plücker直线表达的配准模型, 充分利用了直线的几何约束能力, 使配准模型形式更加简洁。本文使用直线特征代替传统的点特征配准基元, 根据点在配准平面上的几何关系, 采用单位四元数表征点云配准模型, 从而实现配准参数的同步求解, 增强了理论的严密性。该方法不仅适用于遮挡造成的点云配准精度低的问题, 也适用于大旋转角的点云配准。
1 单位四元数表示的旋转运动四元数的基本定义为[8]:
| $ \mathit{\boldsymbol{\widehat h}} = {h_0} + {h_x}{\rm{i}} + {h_y}{\rm{j}} + {h_z}{\rm{k}} $ | (1) |
式中, i、j、k为虚数单位, h0和hx、hy、hz分别为实部和虚部。
若四元数
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {h_0^2 + h_x^2 - h_y^2 - h_z^2}&{2{h_x}{h_y} - 2{h_0}{h_z}}&{2{h_x}{h_z} + 2{h_0}{h_y}}\\ {2{h_x}{h_y} + 2{h_0}{h_z}}&{h_0^2 - h_x^2 + h_y^2 - h_z^2}&{2{h_y}{h_z} - 2{h_0}{h_x}}\\ {2{h_x}{h_z} - 2{h_0}{h_y}}&{2{h_y}{k_z} + 2{h_0}{h_x}}&{h_0^2 - h_x^2 - h_y^2 + h_z^2} \end{array}} \right] $ | (2) |
则旋转参数可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\tan \alpha = - {\mathit{\boldsymbol{R}}_{13}}/{\mathit{\boldsymbol{R}}_{33}}}\\ {\sin \beta = - {\mathit{\boldsymbol{R}}_{23}}}\\ {\tan \gamma = {\mathit{\boldsymbol{R}}_{21}}/{\mathit{\boldsymbol{R}}_{22}}} \end{array}} \right. $ | (3) |
点云配准是一种刚体变换[10], 其形式为:
| $ {\left[ {\begin{array}{*{20}{l}} X\\ Y\\ Z \end{array}} \right]_Q} = \mathit{\boldsymbol{R}}{\left[ {\begin{array}{*{20}{l}} X\\ Y\\ Z \end{array}} \right]_P} + \left[ {\begin{array}{*{20}{l}} {\Delta X}\\ {\Delta Y}\\ {\Delta Z} \end{array}} \right] $ | (4) |
式中, XQ、YQ、ZQ为基准测站Q坐标系下的坐标, XP、YP、ZP为待配准测站P坐标系下的坐标, R为ai、bi、ci(i= 1, 2, 3)等元素组成的旋转矩阵, ΔX、ΔY、ΔZ为待配准测站P坐标系转换到基准测站Q坐标系下的平移参数。
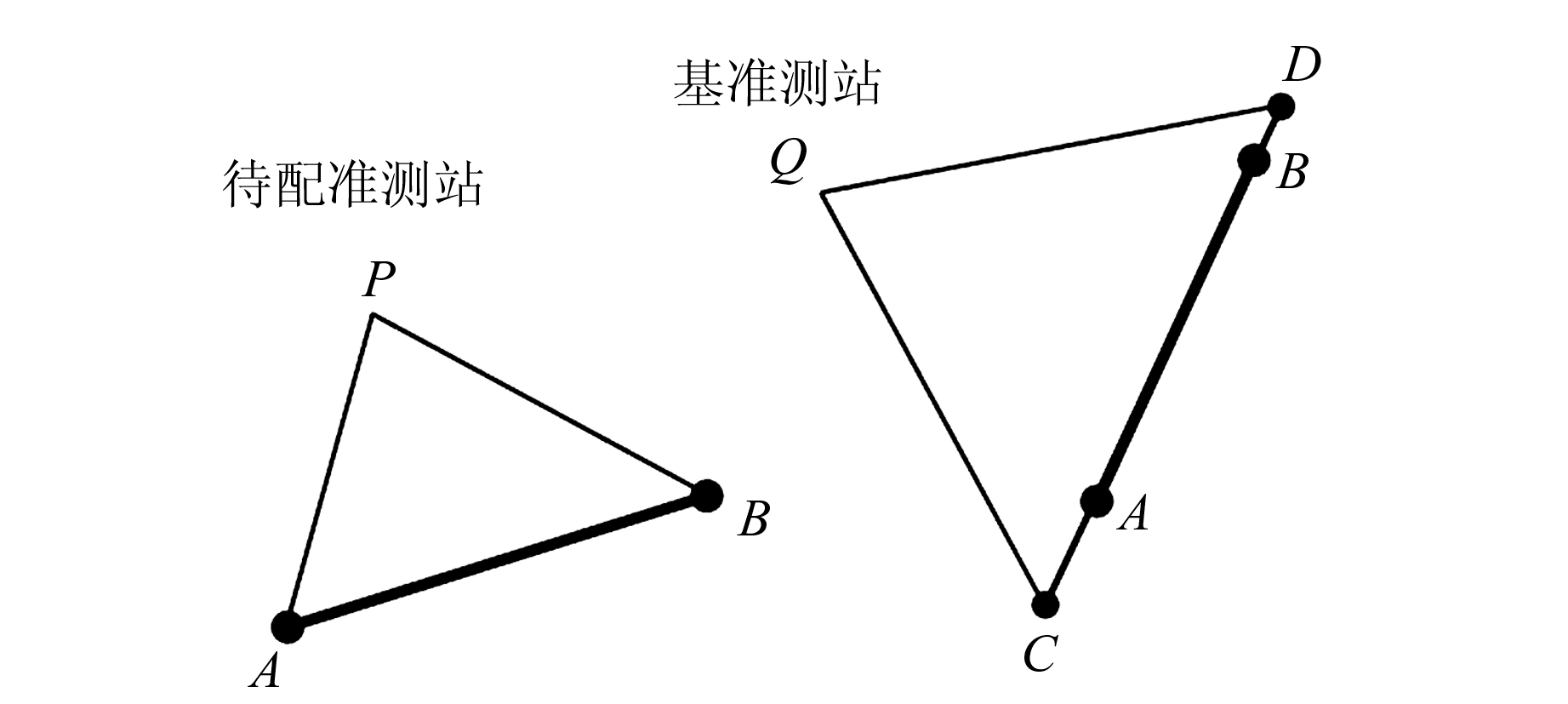
2.2 线基元点云配准模型如图 1所示, 从待配准测站P坐标系和基准测站Q坐标系下的点云数据上提取直线段AB和CD(AB、CD为同名直线段, 但端点不一定为同名点), 其中点A和点B在P坐标系下的坐标为(XPA, YPA, ZPA)和(XPB, YPB, ZPB), 点A和点B在Q坐标系下的坐标(均按式(4)表示)为(XQA, YQA, ZQA)和(XQB, YQB, ZQB), 点P在Q坐标系下的坐标为(ΔX, ΔY, ΔZ), 点C和点D在Q坐标系下的坐标为(XQC, YQC, ZQC)和(XQD, YQD, ZQD)。若点云数据完成配准, 则平面PAB与平面QCD完全重合, 即点A和点B到平面PCD的距离应为0。基于此, 利用单位四元数来描述基于线基元的点云配准模型。
|
图 1 线基元点云配准示意图 Fig. 1 Point cloud registration diagram based on line primitive |
平面QCD的法向量n(nQx, nQy, nQz)(用Q坐标系下的坐标表示)为:
| $ \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{PC}} \times \mathit{\boldsymbol{PD}} $ | (5) |
式中, 向量PC=(XQC-ΔX, YQC-ΔY, ZQC-ΔZ), 向量PD=(XQD-ΔX, YQD-ΔY, ZQD-ΔZ)。
设平面PCD的一般方程为:
| $ Ax + By + Cz + D = 0 $ | (6) |
式中, A=nQx, B=nQy, C=nQz。
由于点P(ΔX, ΔY, ΔZ)在平面PCD上, 故可得D=-nQxΔX-nQyΔY-nQzΔZ, 且点A和点B也在平面PCD上, 即满足式(6), 整理得:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_A} = {n_{Qx}}{{\bar X}_{QA}} + {n_{Qy}}{{\bar Y}_{QA}} + {n_{Qz}}{{\bar Z}_{QA}} = 0}\\ {{F_B} = {n_{Qx}}{{\bar X}_{QB}} + {n_{Qy}}{{\bar Y}_{QB}} + {n_{Qz}}{{\bar Z}_{QB}} = 0} \end{array}} \right. $ | (7) |
式中, XQA=a1XPA+a2YPA+a3ZPA, YQA=b1XPA+b2YPA+b3ZPA, ZQA=c1XPA+c2YPA+c3ZPA, XQB=a1XPB+a2YPB+a3ZPB, YQB=b1XPB+b2YPB+b3ZPB, ZQB=c1XPB+c2YPB+c3ZPB。
2.3 平差模型解算将式(7)按Taylor展开, 取一次项进行线性化, 可得关于点A和点B到平面PCD的距离误差方程式:
| $ \left\{\begin{array}{c} v_{A}=b_{11} \mathrm{d} h_{0}+b_{12} \mathrm{d} h_{x}+b_{13} \mathrm{d} h_{y}+b_{14} \mathrm{d} h_{z}+ \\ b_{15} \mathrm{d} \Delta X+b_{16} \mathrm{d} \Delta Y+b_{17} \mathrm{d} \Delta Z-l_{A} \\ v_{B}=b_{21} \mathrm{d} h_{0}+b_{22} \mathrm{d} h_{x}+b_{23} \mathrm{d} h_{y}+b_{24} \mathrm{d} h_{z}+ \\ b_{25} \mathrm{d} \Delta X+b_{26} \mathrm{d} \Delta Y+b_{27} \mathrm{d} \Delta Z-l_{B} \end{array}\right. $ | (8) |
式中,
若从点云数据中提取n对直线, 则根据式(8)可列出2n个误差方程式, 并表示为矩阵形式:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat X}} - \mathit{\boldsymbol{L}} $ | (9) |
式中, V为2n×1的残差向量, B为2n×7的系数矩阵, L为2n×1的常数项矩阵。其法方程为:
| $ {\mathit{\boldsymbol{N}}_{bb}}\mathit{\boldsymbol{\hat X}} - \mathit{\boldsymbol{W}} = {\rm{0}} $ | (10) |
式中,
由于单位四元数
| $ {\mathit{\boldsymbol{C}}_x}\mathit{\boldsymbol{\hat X}} + {\mathit{\boldsymbol{W}}_x} = 0 $ | (11) |
式中, Cx=[2h0 2hx 2hy 2hz 0 0 0], Wx=h02+hx2+hy2+hz2-1。
联立式(10)和式(11), 至少需要从待配准测站和基准测站的点云数据中提取4对直线段, 依据附有限制条件的间接平差原理[11]求解旋转参数和平移参数。具体实施过程为:
1) 确定参数的初始值:h0 = 1, hx=hy=hz=0, 平移参数ΔX = ΔY= ΔZ =0。
2) 将h0、hx、hy、hz的值代入式(2), 求出旋转矩阵R。
3) 计算参数改正数
4) 判断参数改正数是否均小于限定的阈值:若max{dh0, dhx, dhy, dhz}>ε1=10-6或者max{dΔX, dΔY, dΔZ}>ε2=10-3, 则需要迭代, 重复步骤2)~4), 直至满足要求; 否则, 迭代结束。
5) 迭代终止后, 得到最终的h0、hx、hy、hz代入式(2), 计算旋转矩阵R, 由式(3)确定旋转角度α、β、γ。
3 实验结果及分析本文设计3个实验以验证点云配准算法的正确性及实用性。
3.1 实验1采用文献[12]中的房屋结构点云数据作为数据源, 挑选不同顶点的坐标数据构成直线, 且待配准测站(P坐标系)中的直线段端点与基准测站(Q坐标系)的两端点并不一定完全对应。P坐标系的直线特征的坐标数据见表 1, 本实验模拟了小转角和大转角2种实验方案的配准参数, 具体见表 2, 表 3为本文算法与文献[4]算法的解算结果对比。
|
|
表 1 坐标系P中的直线段坐标数据 Tab. 1 Coordinate data of the line segment in the coordinate system P |
|
|
表 2 配准参数的模拟值 Tab. 2 Simulated values of absolute orientation elements |
|
|
表 3 实验解算结果 Tab. 3 Experimental results |
由表 3可知, 对于小转角(< 3°)和大转角的算例, 本文算法的解算结果与模拟值较为吻合, 证明本文算法是正确有效的。文献[4]算法计算的α最大偏差为0.000 8°, β最大偏差为0.000 2°, γ最大偏差为0.000 7°, ΔX最大偏差为0.000 4 m, ΔY最大偏差为0.000 2 m, ΔZ最大偏差为0.000 1 m; 而本文算法计算的α最大偏差为0.000 2°, β最大偏差为0.000 1°, γ最大偏差为0.000 2°, ΔX最大偏差为0.000 1 m, ΔY最大偏差为0.000 1 m, ΔZ最大偏差为0.000 0 m。由此可知, 本文算法对于模拟数据的计算精度高于文献[4]算法。虽然本文为迭代算法, 但迭代次数均在10次以内, 特别是对于大转角, 并未出现迭代不收敛的现象, 因为本文的点云配准算法是基于单位四元数进行的, 增强了算法的稳定性和适应能力。
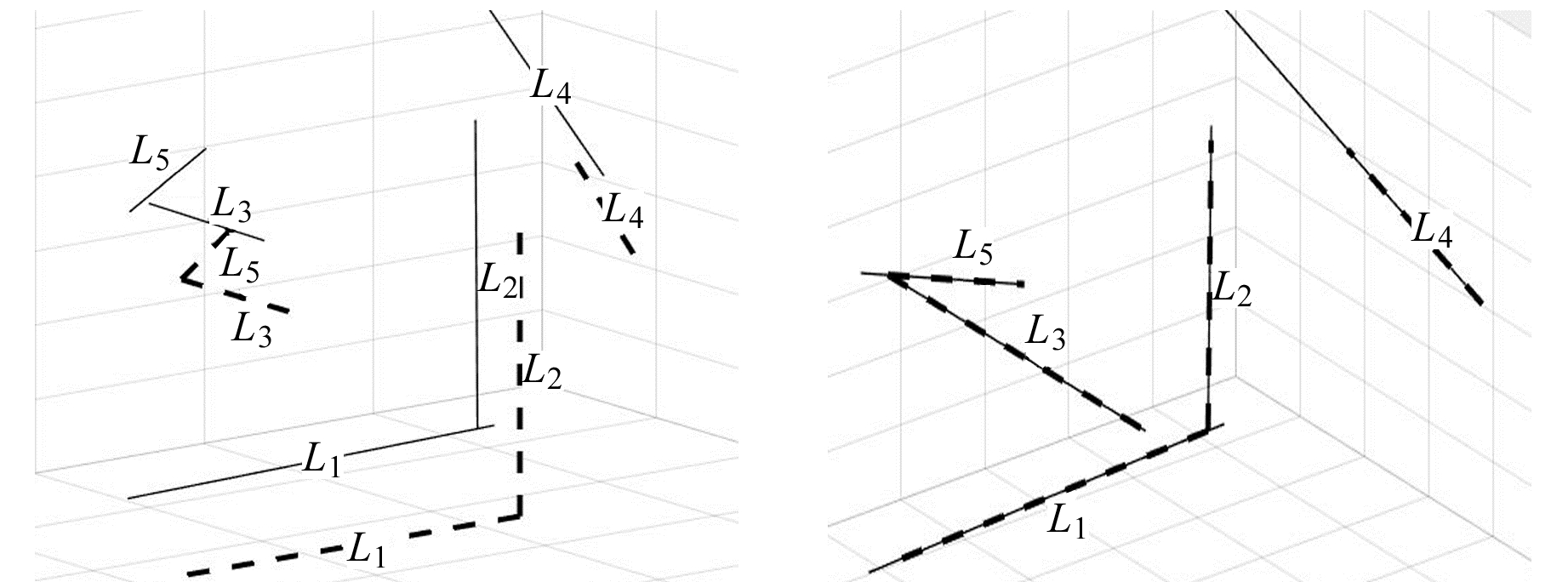
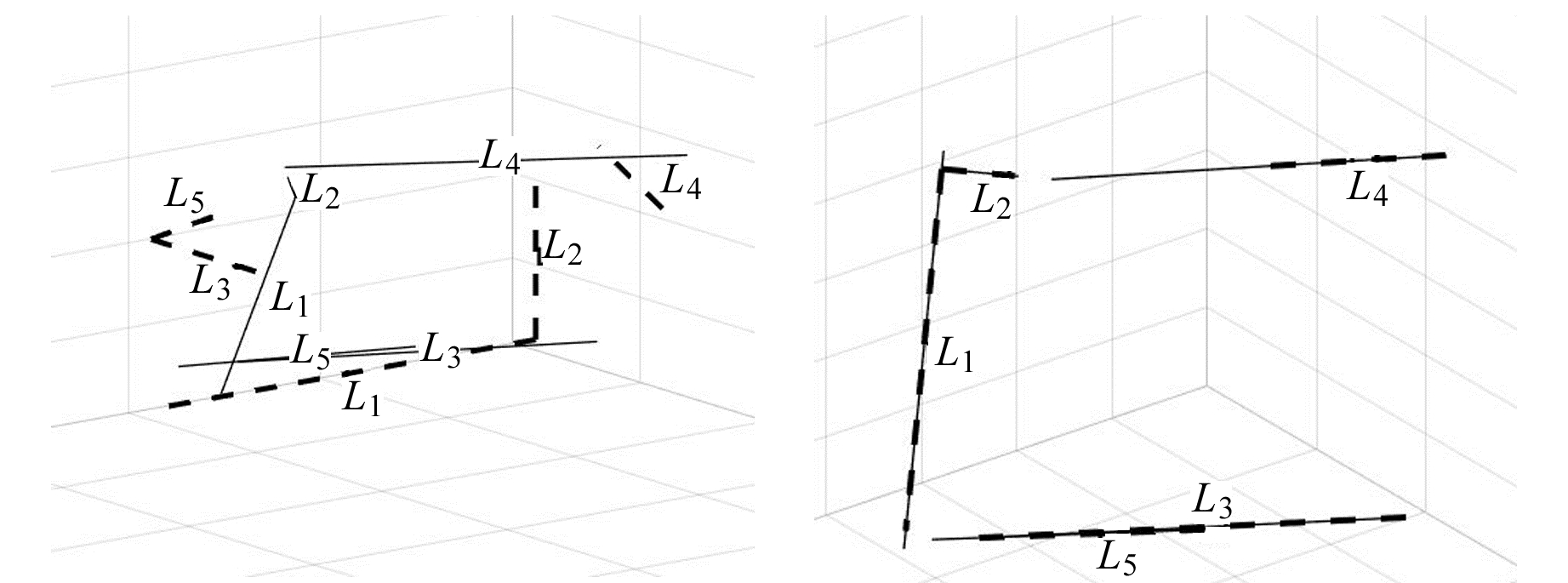
在图 2和3中, 虚线代表待配准测站上的直线, 实线代表基准测站上的直线。由图可知, 在配准前, 小转角数据和大转角数据下待配准测站和基准测站上的同名直线并不重合, 而使用本文基于直线特征的点云配准算法后, 实线和虚线的重合度较高, 说明本文配准算法是可行的。
|
图 2 小转角数据配准前后直线空间分布 Fig. 2 Spatial distribution of lines in small angle data before and after registration |
|
图 3 大转角数据配准前后直线空间分布 Fig. 3 Spatial distribution of lines in big angle data before and after registration |
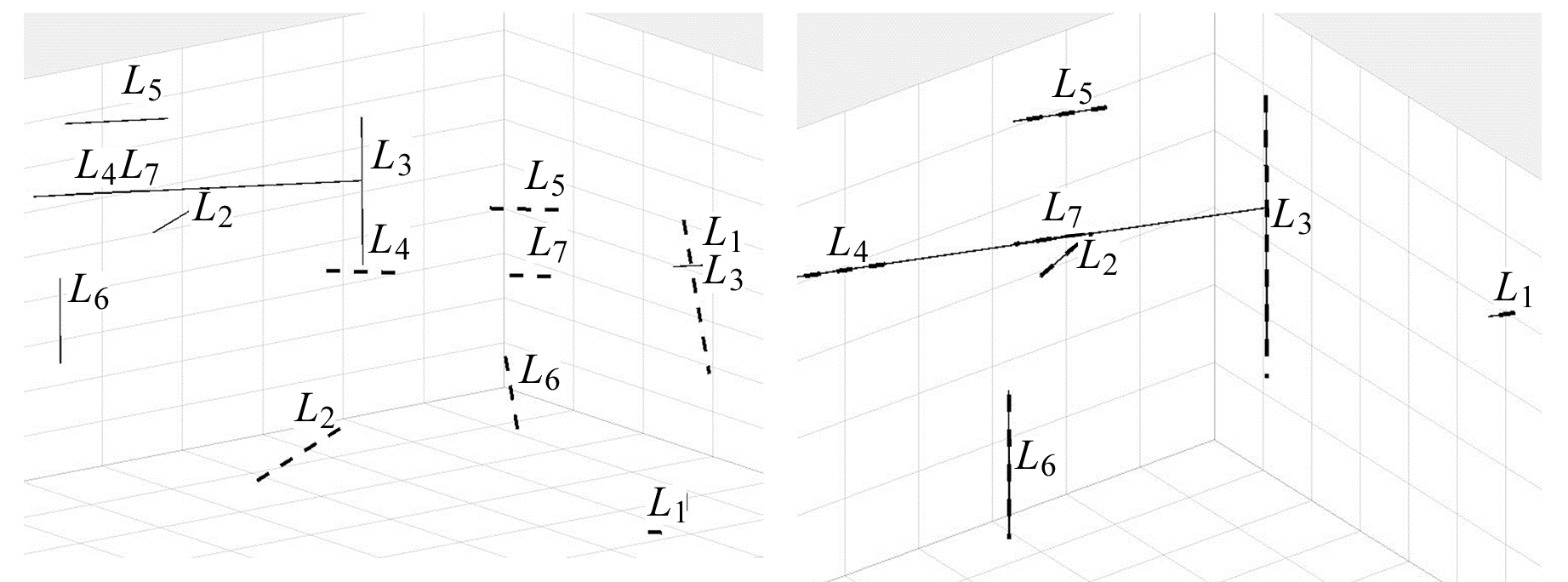
为进一步验证本文算法的可靠性及实用性, 与文献[6]算法进行对比分析。实验采用文献[5]中实测的建筑物立面的LiDAR点云数据, 其中从待配准测站和基准测站中共提取7对同名直线数据, 限于篇幅数据并未完全列出, 配准前后直线的空间分布见图 4。
|
图 4 数据配准前后直线空间分布 Fig. 4 Spatial distribution of straight lines before and after data registration |
本文算法与文献[6]算法的配准结果见表 4, 从解算的旋转矩阵和平移参数来看, 结果比较接近。表 5为配准精度对比, 由表可知, 配准后得到的直线方向向量偏差的中误差相差不大, 本文算法的矩偏差中误差均优于文献[6]算法。结合图 4可以看出, 配准后基准测站直线和待配准测站直线重合, 证明本文算法能够正确实现配准。
|
|
表 4 不同算法配准结果 Tab. 4 Registration results of different algorithms |
|
|
表 5 不同算法的配准精度对比 Tab. 5 Registration accuracy comparison of different algorithms |
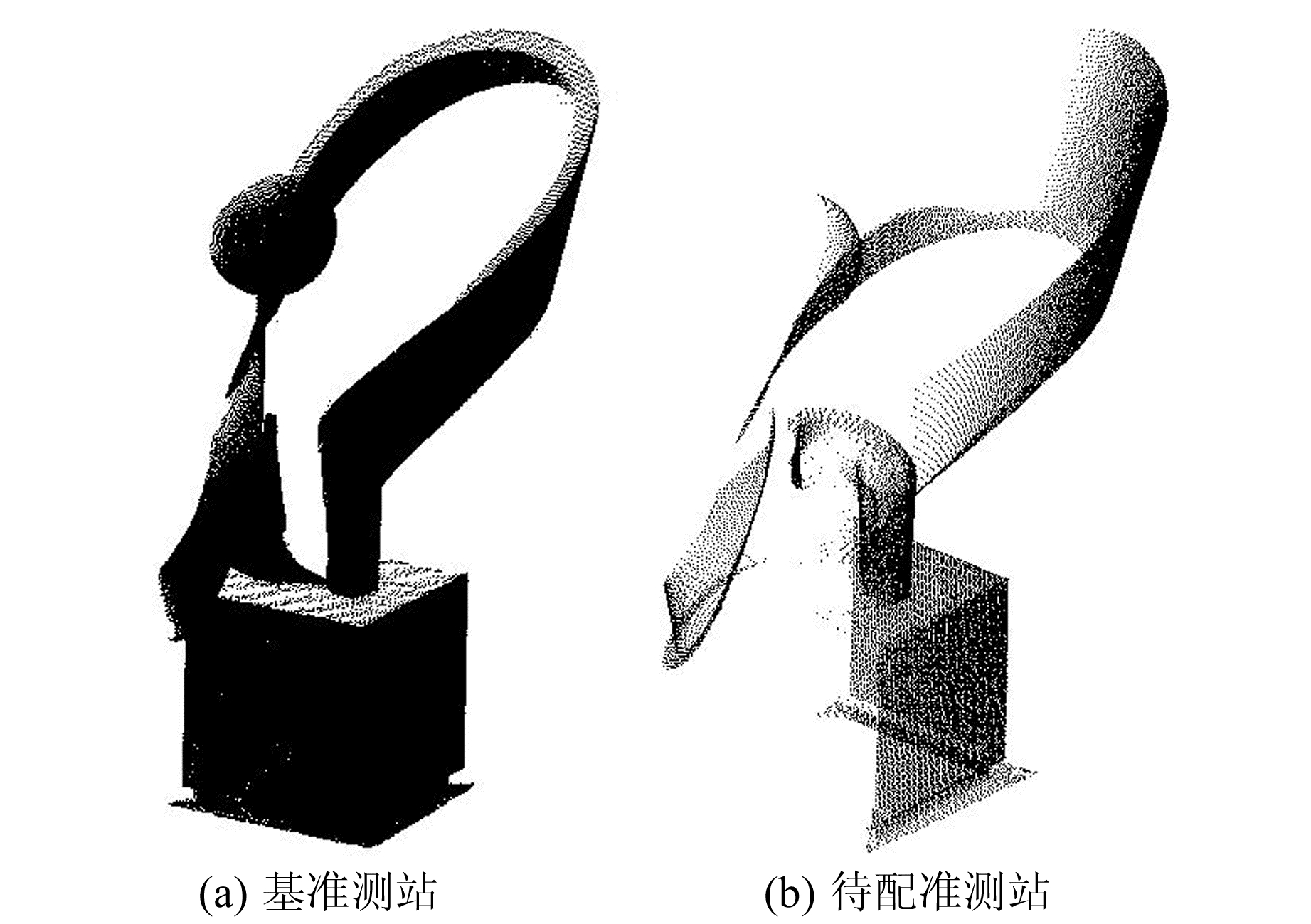
实验3利用三维激光扫描仪获取太原理工大学虎峪校区训练馆前的一个标志物的点云数据, 共扫描4站点云, 对点云数据进行精简去噪后, 选择第1测站数据作为基准测站数据(图 5(a)), 第4测站的点云数据作为待配准测站数据(图 5(b)), 共选取4对同名直线, 空间分布见图 6。
|
图 5 点云数据 Fig. 5 Point cloud data |
|
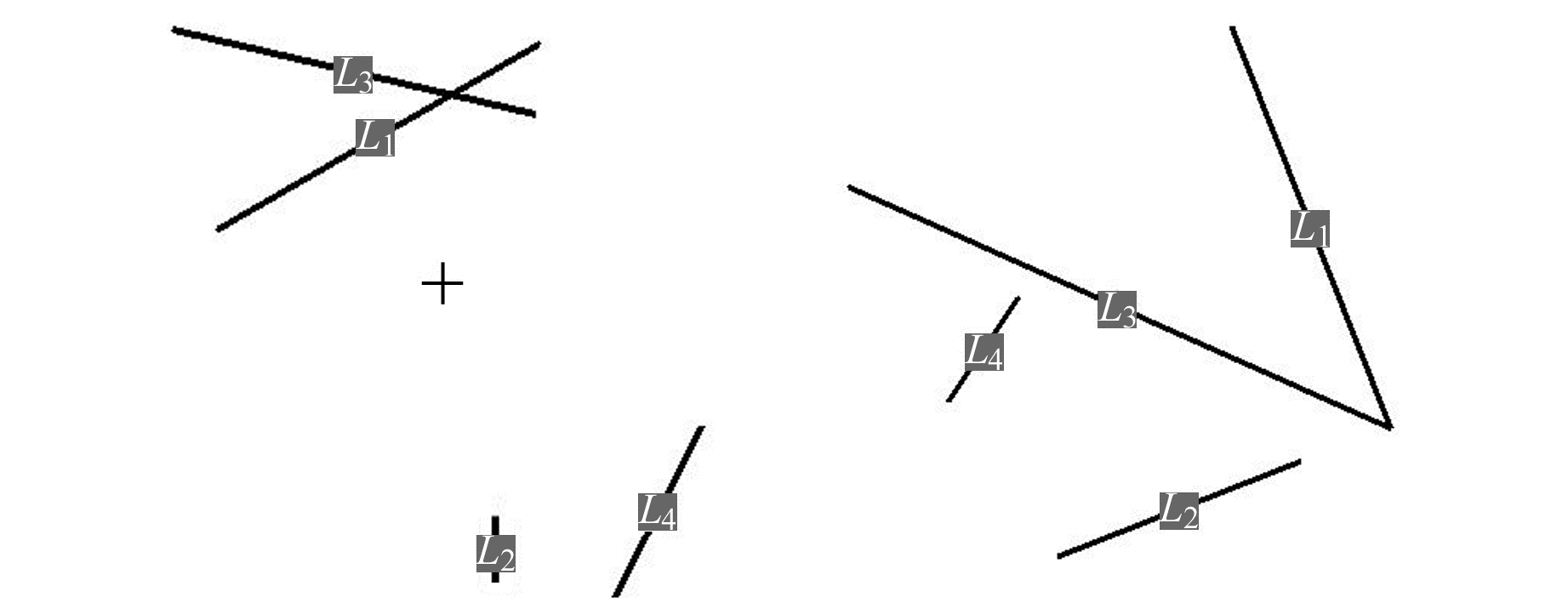
图 6 从基准测站和待配准测站提取的直线的空间分布 Fig. 6 Spatial distribution of the extracted lines from reference and unregistration station |
由图 6可以看出, 从基准测站和待配准测站提取的同名直线端点并不是同名点。对比本文算法与文献[4]算法, 配准结果和配准精度见表 6和7。由表 6、7可以看出, 2种算法的配准参数比较接近, 文献[4]算法与本文算法计算的单位方向向量偏差中误差都为0.000 1 m, 而矩向量偏差分别为0.015 8 m和0.013 1 m, 本文算法稍优于文献[4]算法。主要是因为文献[4]算法是先计算旋转矩阵, 后计算平移向量, 平移向量的计算依赖于旋转矩阵; 而本文算法实现了旋转矩阵和平移向量的同步求解, 从而提高了计算精度。由图 7可以看出, 依据本文算法计算的配准参数, 基准测站和待配准测站的点云数据能较好地拼接在一起。
|
|
表 6 不同算法配准结果 Tab. 6 Registration results of different algorithms |
|
|
表 7 不同算法的配准精度对比 Tab. 7 Registration accuracy comparison of different algorithms |

|
图 7 配准后目视效果 Fig. 7 Visual effect after registration |
从应用方面来看, 本文推导的线特征点云配准模型能够克服传统的基于点特征的配准算法不能解决缺少完全对应的同名特征点不足的问题, 且不要求同名直线段的端点具有一致性。同时, 由于采用单位四元数进行描述, 线性化程度较高, 对于大转角也能较快收敛, 对初值的依赖性也降低。从实验结果来看, 该模型具有一定的实用价值。
| [1] |
Besl P J, Mckay N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256 DOI:10.1109/34.121791
(  0) 0) |
| [2] |
盛庆红, 陈姝文, 秦坤, 等. 利用Plücker直线的点云与立体影像配准[J]. 计算机辅助设计与图形学学报, 2016, 28(3): 450-455 (Sheng Qinghong, Chen Shuwen, Qin Kun, et al. Registration of Stereo Images with Point Clouds Using Plücker Line[J]. Journal of Computer-Aided Design and Computer Graphics, 2016, 28(3): 450-455 DOI:10.3969/j.issn.1003-9775.2016.03.010)
(  0) 0) |
| [3] |
Guan Y L, Zhang H J. Initial Registration for Point Clouds Based on Linear Features[C]. Fourth International Symposium on Knowledge Acquisition and Modeling, Sanya, 2011
(  0) 0) |
| [4] |
王永波, 杨化超, 刘燕华, 等. 线状特征约束下基于四元数描述的LiDAR点云配准方法[J]. 武汉大学学报:信息科学版, 2013, 38(9): 1 057-1 062 (Wang Yongbo, Yang Huachao, Liu Yanhua, et al. Linear-Feature-Constrained Registration of LiDAR Point Cloud via Quaternion[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1 057-1 062)
(  0) 0) |
| [5] |
王永波, 汪云甲, 佘雯雯, 等. 直线特征约束下利用Plücker坐标描述的LiDAR点云无初值配准方法[J]. 武汉大学学报:信息科学版, 2018, 43(9): 1 376-1 384 (Wang Yongbo, Wang Yunjia, She Wenwen, et al. A Linear Features-Constrained, Plücker Coordinates-Based, Closed-Form Registration Approach to Terrestrial LiDAR Point Clouds[J]. Geomatics and Information Science of Wuhan University, 2018, 43(9): 1 376-1 384)
(  0) 0) |
| [6] |
盛庆红, 陈姝文, 柳建锋, 等. 基于Plücker直线的LiDAR点云配准法[J]. 测绘学报, 2016, 45(1): 58-64 (Sheng Qinghong, Chen Shuwen, Liu Jianfeng, et al. LiDAR Point Cloud Registration Based on Plücker Line[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 58-64)
(  0) 0) |
| [7] |
盛庆红, 张斌, 肖晖, 等. 直线簇约束下的地面LiDAR点云配准方法[J]. 武汉大学学报:信息科学版, 2018, 43(3): 406-412 (Sheng Qinghong, Zhang Bin, Xiao Hui, et al. A Registration Method Based on Line Cluster for Terrestrial LiDAR Point Clouds[J]. Geomatics and Information Science of Wuhan University, 2018, 43(3): 406-412)
(  0) 0) |
| [8] |
王力, 李豪, 姜卫平. 一种基于四元数的三维基准转换简便模型[J]. 大地测量与地球动力学, 2015, 35(2): 243-247 (Wang Li, Li Hao, Jiang Weiping. A Simplified Model of Quaternion-Based Three-Dimensional Datum Transformation[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 243-247)
(  0) 0) |
| [9] |
李志伟, 李克昭, 赵磊杰, 等. 基于单位四元数的任意旋转角度的三维坐标转换[J]. 大地测量与地球动力学, 2017, 37(1): 81-85 (Li Zhiwei, Li Kezhao, Zhao Leijie, et al. Three-Dimensional Coordinate Transformation Adapted to Arbitrary Rotation Angles Based on Unit Quaternion[J]. Journal of Geodesy and Geodynamics, 2017, 37(1): 81-85)
(  0) 0) |
| [10] |
张会霞, 朱文博. 三维激光扫描数据处理理论及应用[M]. 北京: 电子工业出版社, 2012 (Zhang Huixia, Zhu Wenbo. Theory and Application of 3D Laser Scanning Data Processing[M]. Beijing: Publishing House of Electronics Industry, 2012)
(  0) 0) |
| [11] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2014 (Discipline Group of Surveying Adjustment, School of Surveying and Mapping, Wuhan University. Error Theory and the Basis of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2014)
(  0) 0) |
| [12] |
Lasenby J, Fitzgerald W J, Lasenby A N, et al. New Geometric Methods for Computer Vision: An Application to Structure and Motion Estimation[J]. International Journal of Computer Vision, 1998, 26(3): 191-213 DOI:10.1023/A:1007901028047
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


