2. 中国地震局地壳应力研究所, 北京市安宁庄路1号, 100085
地面三维激光扫描仪(地基LiDAR)具有使用简便、易携带等优势, 在地学研究中应用广泛, 可以快速构建微地貌地形的高精度数字高程模型(digital elevation model, DEM)。但在相对复杂的地形地貌中, 由于一些不确定因素(仪器抖动、地形遮挡或站点布设不合理等)的影响, 会造成局部数据的缺失。为更好地获取特定区域全面的高精度DEM, 在数据处理时需对遗漏区域进行空间插值处理。
目前, 针对点云数据采用不同插值方法和不同评价手段等进行插值技术的研究大多基于机载LiDAR[1-2]。本文以地基LiDAR为载体, 对冷龙岭断裂带的典型陡坎进行点云数据采集(图 1)。由于研究区地形复杂及站点布设不合理、动植物遮挡、仪器抖动、天气等因素的影响, 点云数据会有局部遗失的情况(图 2), 本文在进行多种插值方法的填充对比分析后, 得出一种更适合于地基LiDAR的点云数据遗失的插值填充方法, 为后期点云DEM的构建和微地形地貌的研究提供技术指导和数据保证。

|
箭头指向为断层陡坎位置 图 1 冷龙岭断裂带局部遥感影像 Fig. 1 Local remote sensing image of Lenglongling fault zone |

|
黑色区域代表数据遗漏,红色代表站点布设 图 2 点云数据缺失 Fig. 2 Data omission in point cloud |
地基LiDAR由1台激光测距仪和1组反射棱镜组成, 其中激光测距仪的作用是主动发射激光和接收从物体表面反射回的信号, 而发射棱镜则起到引导激光完成对目标物进行扫描的作用[3]。地基LiDAR不仅可以获得各个点的数据信息(距离值S、水平方向角α、垂直方向角度β、仪器姿态参数及激光点的反射强度R), 还可以搭载数码相机来存储激光点的颜色信息(R、G、B), 通过专业软件对数据进行可视化处理, 便可直观地看到激光点云影像[4](图 3)。

|
图 3 激光点云影像 Fig. 3 Laser point cloud image |
与其他影像数据相比, 点云影像既有优势也有局限性。其优势包括:1)可测量点坐标及点与点之间的距离等信息; 2)高密度、高精度、高分辨率, 离扫描仪最近的点位间距达到mm级甚至亚mm级; 3)扫描仪所搭载的相机可获取物体表面的真彩色(RGB)信息(图 3(b))。其局限性有:1)由于扫描角的限制, 固定式三维激光扫描仪的覆盖面积有限, 导致点云数据有局限性; 2)扫描测量存在误差; 3)扫描时由于不确定因素的影响, 会产生数据的缺失; 4)不规则性和不连续性; 5)仪器发射的激光为近红外, 不能穿透物体本身, 获取的点云数据只能呈现物体的表面信息。
1.2 数据采集与处理地基LiDAR的整体操作流程可分为2个部分, 分别是点云采集和点云处理分析。其中, 点云采集主要包括研究区选择、站点布设、参数设置、数据采集等; 点云处理分析主要有点云预处理(点云滤波、点云拼接、坐标转换)和点云应用分析(插值填充、三维建模、应用分析)。为确保后期研究成果的严谨性和可靠性, 点云数据的精度和可靠性必须满足2个要求:1)在点云采集时, 单次扫描精度为5 mm; 2)在数据处理过程中, 各站测点元数据的拼接标准差必须小于0.005 mm。
2 空间插值算法依据数学本质和插值方法的基本假设[5-6], 将最邻近插值法(nearest neighbor, NN)、距离反比插值法(inverse distance weighted interpolation, IDW)、不规则三角网插值法(triangulated irregular network, TIN)、样条函数插值法(spline)、克里金插值法(Kriging)划分为几何模型插值法、函数模型插值法及随机模型插值法[7-10]。以冷龙岭断裂带楚马源段典型地貌数据(图 4)为例, 利用不同插值法进行填充并对比, 从中选取更为合理的点云数据插值方法。
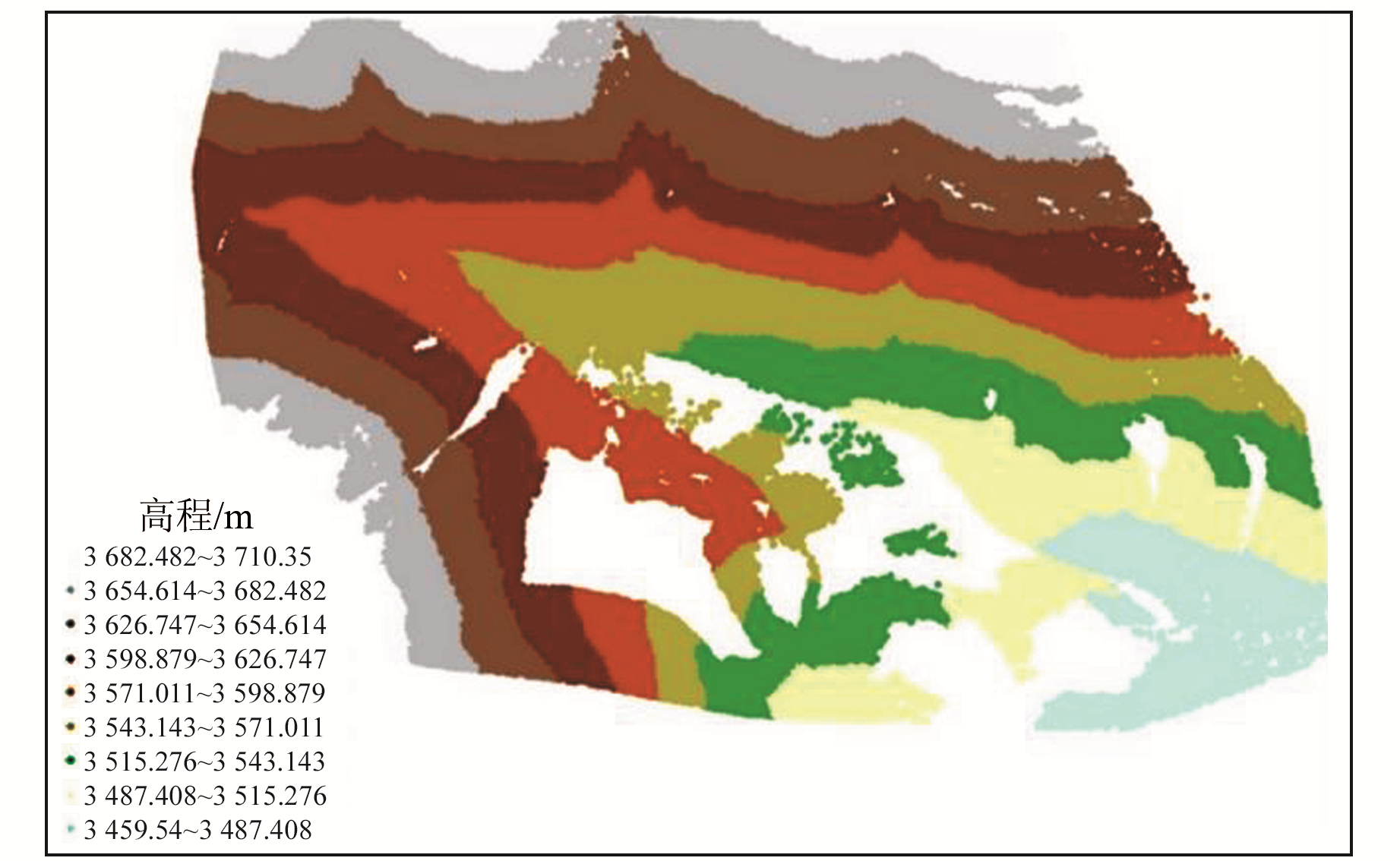
|
白色区域为数据遗漏 图 4 楚马源段原始点云数据 Fig. 4 The original point cloud data of Chumayuan section |
最邻近插值法又被称为泰森多边形分析法, 是一位气象学家为估算平均降雨量而提出的一种方法, 目前被应用于GIS分析的快速赋值[11]。其工作原理是在计算中先确定待插点周边最近的3点位置, 由此确定一个平面, 进而推算出待插点的高程。最邻近插值法适合于数据分布均匀或高密度数据中只有少数没有属性值的情况[10], 其插值效果见图 5。由图可知, 插值的整体效果好, 可以较完整地表现该区的地形地貌, 但当边界放大时, 可以看出边界具有锯齿效应。
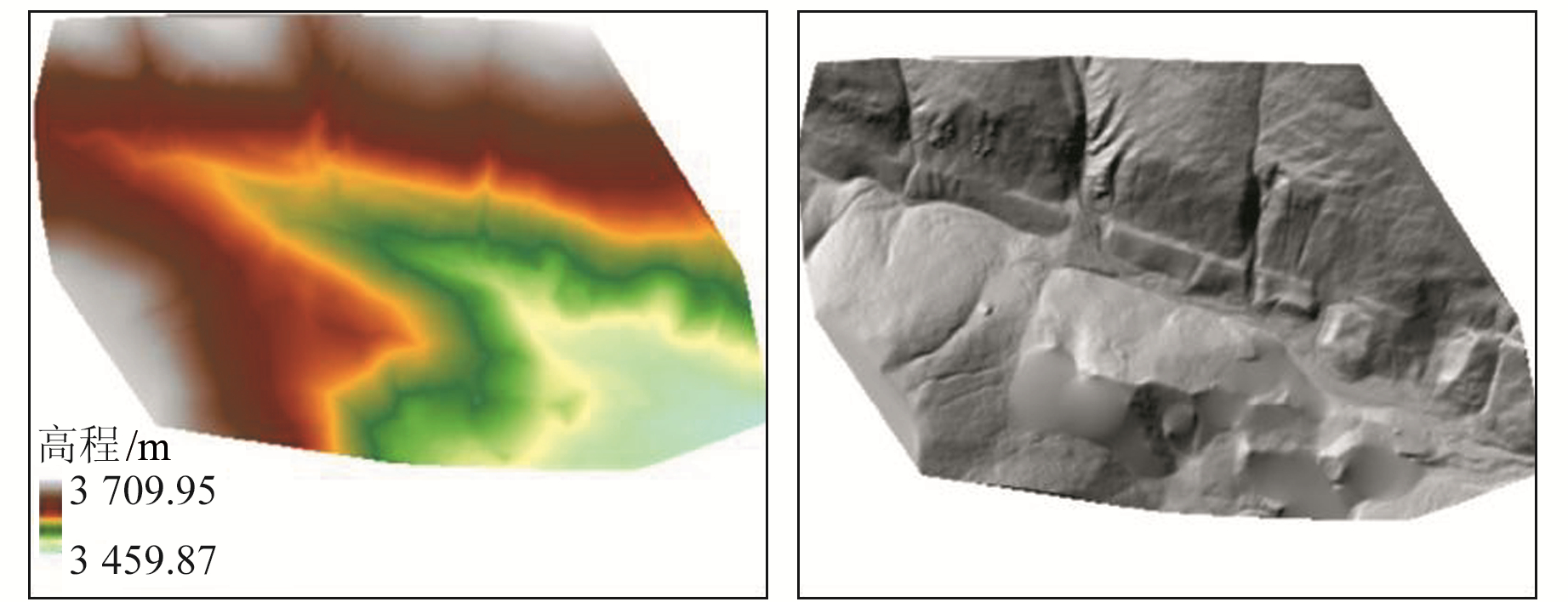
|
图 5 插值效果图及阴影图 Fig. 5 Interpolation effect image and shadow image |
距离反比插值法是美国国家气象局在1972年提出的, 其原理是在未知点周边选取一些样本点, 距离近的样本点对未知点的属性信息有很大影响, 且两者成反比, 利用待插点与周边取样点之间的距离为权重进行插值, 即P点的高程值Z可以表示为:
| $ {Z_P} = \sum\limits_{i = 1}^n {\frac{{{Z_i}}}{{d_i^2}}} /\sum\limits_{i = 1}^n {\frac{1}{{d_i^2}}} $ |
式中, di为待插点与周边第i个取样点的距离, 其插值效果见图 6。可以看出, 在缺值区域内距离较远处的插值效果差, 并影响有点区域的效果, 因此无法估计误差。

|
图 6 插值效果图及阴影图 Fig. 6 Interpolation effect image and shadow image |
不规则三角网插值法是以取样点和断线等要素为基础来近似表示物体表面的方法, 其面的形状为三角形, 大小取决于采样点的密度和具体位置, 与地形的实际特征相吻合, 对于一些包含大量特征的地形, 该方法能更好、更精确地还原真实地形[12]。该插值法的原理是:通过进行三角形构建, 组成一张能覆盖整个区域的格网, 且构建的三角形不能相交, 每个三角形覆盖的节点的面都被定义为已知信息, 建成三角形的所有点都受三角形的表面限制。通过插值效果(图 7)可以看出, 不规则三角网插值法能很好地表现该地区的地形地貌, 插值效果相对稳定, 但前期数据处理工作量较大。

|
图 7 插值效果图及阴影图 Fig. 7 Interpolation effect image and shadow image |
样条函数插值法对属性值的估算是采用函数中的最小化表面总曲率进行的, 样条函数是分段函数, 拐点处可以进行求导, 即可对少数采样点配准进行修改, 无需对整条曲线进行计算[8, 13]。该方法的优势是容易操作、计算量小, 常应用于表面非常平滑的情况, 其基本要求是有连续的1阶和2阶导数, 且采样点的密集程度较高。该方法的缺点是无法估计误差, 当点的密度较小时, 插值效果不好, 其插值效果见图 8。由图可知, 样条函数插值法改变了整体的地形地貌效果, 生成的曲面较平滑, 但高程值的改变较大。

|
图 8 插值效果图及阴影图 Fig. 8 Interpolation effect image and shadow image |
克里金插值法的基本原理是假设物体属性的空间变化不是随机的且不是全部确定的, 应采用随机的表面给予合理的表示。该方法对空间目标物的位置变异分布进行研究, 找出合适的距离范围, 这个范围的锁定对未知点有很大的影响, 最后根据数学公式利用范围内的已知点推算出未知点的基本属性[7-8]。
假设Z(x, y)为稳态随机过程, 其离散值为Z(xi, yi), 对未知点P(xp, yp)的高程属性进行计算, 其解为:
| $ Z\left( {{x_p}, {y_p}} \right) = \sum\limits_{i = 1}^n {{\beta _i}} Z\left( {{x_p}, {y_p}} \right) $ |
式中, βi为待定Kriging权, βi需满足的条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{\beta _i}} = 1}\\ {{\mathop{\rm var}} \left[ {Z\left( {{x_i}, {y_i}} \right) - \sum\limits_i^n {{\beta _i}} Z\left( {{x_i}, {y_i}} \right)} \right] = \min } \end{array}} \right. $ |
式中, var表示方差。由此可得出βi的求解方程组, 即可算出未知点的高程信息。该方法的插值效果见图 9。因其变异函数的确定需要人为经验, 所以处理效果不好, 对缺值区域处理不理想, 且计算量大, 需要很长的计算时间。
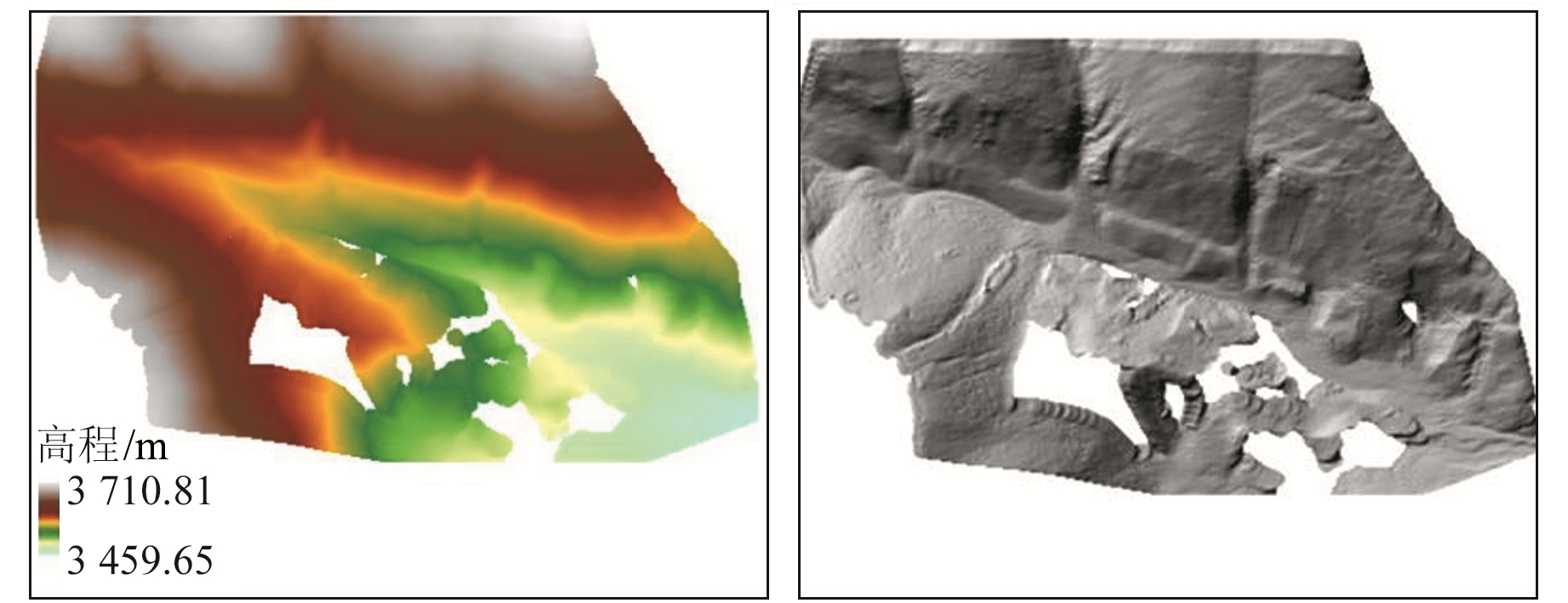
|
图 9 插值效果图及阴影图 Fig. 9 Interpolation effect image and shadow image |
为使各插值方法的结果具有一定的可比性, 将输出单元格大小(设为2.2)、距离指数(设为2)、采样点数(设为12)等参数设为相同值, 最后从时间、精度及平滑能力等方面作比较分析, 得出各插值方法的优缺点及运算效率, 见表 1。由表可知, 距离反比插值法对地形地貌的处理出现错误, 对点云缺失地区的处理效果最差, 不能很好地应用于LiDAR点云数据的插值中。最邻近插值法和不规则三角网插值法都能很好地对缺失点进行插值填充, 整体效果基本相同。但从局部放大的效果看, 最邻近插值法没有不规则三角网插值法的效果好, 其有明显的边缘锯齿效应。且由图 10可以看出, 不规则三角网插值法的效果也高于最邻近插值法。克里金插值法对特征属性信息的估算更加精准, 但耗时最长, 工作效率低, 且对人为经验有很高的要求。样条函数插值法与距离反比插值法的插值效果都很差, 且样条函数插值法会对高程值有大幅度的改变[1]。
|
|
表 1 不同插值法对比 Tab. 1 Comparison of different interpolation methods |

|
图 10 局部效果对比 Fig. 10 Comparison of local effect |
从运算效率和插值结果来看, 不规则三角网插值法对地形点云遗漏的填充结果最优。其可以根据地形起伏变化对取样点的密度和位置进行选择, 较好地避免因地形平坦产生的数据冗余, 并将地形上的特征点(山谷、山脊等)以数字高程特征表示, 具体结果见图 11。因此, 对于地基LiDAR的点云遗漏采用不规则三角网插值法可以更好地还原野外真实场景, 并获取高精度(0.05 m)的DEM和等高距为1 m的等高线效果图(图 12)。

|
图 11 TIN插值效果及野外照片 Fig. 11 TIN interpolation effect and field photo |

|
图 12 DEM和等高线 Fig. 12 DEM and contour |
对于地基LiDAR获取的地形点云数据在采集过程中受不定因素的影响造成局部缺失的情况, 本文将5种常用的插值方法分为3大类, 分别对研究区进行插值, 并对结果进行对比分析。结果表明, 3类插值方法都是建立在一定的假设基础之上的, 且都有一定的局限性:几何模型插值法只考虑目标物表面的几何关系, 函数模型插值法只考虑目标物表面的趋势关系, 而随机模型插值法只考虑目标物表面的统计关系。以冷龙岭断裂带上一处典型陡坎地形的点云数据为例, 从插值效率和效果中可以看出, 不规则三角网插值法(TIN)更适合于地基LiDAR所获取的地形地表点云数据缺失的插值, 能快速、较好地还原真实的野外场景, 为后期该地区活断层微地貌地形信息的提取、三维建模及定量化研究等提供数据保证。
| [1] |
徐巍, 孙志鹏, 徐朋, 等. 基于LiDAR点云数据插值方法研究[J]. 工程地球物理学报, 2012, 9(3): 365-370 (Xu Wei, Sun Zhipeng, Xu Peng, et al. Interpolation Method Based on the Point Cloud Data LiDAR[J]. Chinese Journal of Engineering Geophysics, 2012, 9(3): 365-370)
(  0) 0) |
| [2] |
杨秋丽, 魏建新, 郑江华, 等. 离散点云构建数字高程模型的插值方法研究[J]. 测绘科学, 2019, 44(7): 16-23 (Yang Qiuli, Wei Jianxin, Zheng Jianghua, et al. Comparison of Interpolation Methods of Digital Elevation Model Using Discrete Point Cloud Data[J]. Science of Surveying and Mapping, 2019, 44(7): 16-23)
(  0) 0) |
| [3] |
焦其松, 张景发, 蒋洪波, 等. 基于TLS技术的典型建筑物震害信息三维建模分析——以彭州市白鹿中学为例[J]. 国土资源遥感, 2016, 28(1): 166-171 (Jiao Qisong, Zhang Jingfa, Jiang Hongbo, et al. Typical Earthquake Damage Extraction and Three-Dimensional Modeling Analysis Based on Terrestrial Laser Scanning:A Case Study of Bailu Middle School of Pengzhou City[J]. Remote Sensing for Land and Resources, 2016, 28(1): 166-171)
(  0) 0) |
| [4] |
袁小祥, 王晓青, 窦爱霞, 等. 基于地面LiDAR玉树地震地表破裂的三维建模分析[J]. 地震地质, 2012, 34(1): 39-46 (Yuan Xiaoxiang, Wang Xiaoqing, Dou Aixia, et al. Terrestrial LiDAR-Based 3D Modeling Analysis of Surface Rupture Caused by Yushu Earthquake[J]. Seismology and Geology, 2012, 34(1): 39-46)
(  0) 0) |
| [5] |
李朝奎, 陈良, 王勇. 降雨量分布的空间插值方法研究——以美国爱达荷州为例[J]. 矿产与地质, 2007, 21(6): 684-687 (Li Chaokui, Chen Liang, Wang Yong. Research on Spatial Interpolation of Rainfall Distribution——A Case Study of Idaho State in the USA[J]. Mineral Resources and Geology, 2007, 21(6): 684-687)
(  0) 0) |
| [6] |
王兴, 刘莹, 王春晖, 等. 海洋盐度分布的插值方法应用与对比研究[J]. 海洋通报, 2016, 35(3): 324-330 (Wang Xing, Liu Ying, Wang Chunhui, et al. Study on the Application and Comparison of Interpolation Methods for the Marine Salinity Distribution[J]. Marine Science Bulletin, 2016, 35(3): 324-330)
(  0) 0) |
| [7] |
朱求安, 张万昌, 余钧辉. 基于GIS的空间插值方法研究[J]. 江西师范大学学报:自然科学版, 2004, 28(2): 183-188 (Zhu Qiu'an, Zhang Wanchang, Yu Junhui. The Spatial Interpolations in GIS[J]. Journal of Jiangxi Normal University: Natural Sciences Edition, 2004, 28(2): 183-188)
(  0) 0) |
| [8] |
李新, 程国栋, 卢玲. 空间内插方法比较[J]. 地球科学进展, 2000, 15(3): 260-265 (Li Xin, Cheng Guodong, Lu Ling. Comparison of Spatial Interpolation Methods[J]. Advances in Earth Science, 2000, 15(3): 260-265)
(  0) 0) |
| [9] |
黄杏元, 马劲松, 汤勤. 地理信息系统概论[M]. 北京: 高等教育出版社, 2001 (Huang Xingyuan, Ma Jinsong, Tang Qin. Introduction to Geographic Information System[M]. Beijing: Higher Education Press, 2001)
(  0) 0) |
| [10] |
张昊, 蒋立辉, 汪承义. 基于LiDAR点云生成DSM的插值方法研究[J]. 现代电子技术, 2007, 30(11): 4-6 (Zhang Hao, Jiang Lihui, Wang Chengyi. Study on Data Interpolation Algorithms for Creating DSM from LiDAR Point Cloud[J]. Modern Electronics Technique, 2007, 30(11): 4-6)
(  0) 0) |
| [11] |
Manry C W, Broschat S L, Schneider J B. Higher-Order FDTD Methods for Large Problems[J]. Applied Computational Electromagnetics Society Journal, 1995, 10(2): 17-29
(  0) 0) |
| [12] |
姚艳丽, 蒋胜平, 王红平. 基于地面三维激光扫描仪的滑坡整体变形监测方法[J]. 测绘地理信息, 2014, 39(1): 50-53 (Yao Yanli, Jiang Shengping, Wang Hongping. Overall Deformation Monitoring for Landslide by Using Ground 3D Laser Scanner[J]. Journal of Geomatics, 2014, 39(1): 50-53)
(  0) 0) |
| [13] |
马剑.机载LiDAR数据插值方法研究[D].焦作: 河南理工大学, 2010 (Ma Jian.Research on the Interpolation of Airborne LiDAR[D].Jiaozuo: Henan Polytechnic University, 2010)
(  0) 0) |
2. Institute of Crustal Dynamics, CEA, 1 Anningzhuang Road, Beijing 100085, China
 2020, Vol. 40
2020, Vol. 40

