2. 华东交通大学土木工程国家实验教学示范中心, 南昌市双港东大街808号, 330013
电离层作为近地空间环境的重要组成部分, 对导航定位系统及无线电通信等的精确性和实时性有着重要的影响。电离层在时空上具有无序性、随机性和非线性, 若选取固有模型对电离层电子含量进行预报, 所得精度无法满足应用需求。为探求高精度的电离层总电子含量(TEC)预报模型, 国内外学者开展了广泛的研究, 并取得一定的成果[1-7]。神经网络作为一种典型的非线性模型, 在很多领域得到广泛的应用, 李淑慧等[8]利用神经网络模型预测目标日内12个TEC值, 较好地反映了TEC值的变化特征; 陆建华等[9]建立时间序列与BP神经网络的组合模型对TEC进行短期预报, 预报精度比时间序列模型有所提高。越来越多的研究表明, BP神经网络学习速度较慢, 模型稳定度低, 只是一种常规静态模型。因此, 汤俊等[10]提出用经验模态分解(EMD)与时间序列相结合的模型进行TEC值的预报; 吉长东等[11]提出将EMD与自回归神经网络相结合的方法进行预测。然而, EMD存在模态混叠现象, 会导致信号分解不准确, 影响TEC值的预报精度。
针对这一问题, 本文提出改进的集总平均经验模态分解(MEEMD)[12]和Elman回归神经网络相结合的预报模型, 即MEEMD-ERNN模型, 通过MEEMD对电离层TEC数据进行分解, 从而获取电离层TEC的多个分量, 再利用Elman神经网络(ERNN)模型对其进行预报重构。
1 模型基本原理 1.1 MEEMD的基本思想在分解信号时, 信号中的间歇性成分会导致EMD的二阶滤波网络特性折中, 引起模态混叠。此时, 分解得到的本征式分量(IMF)会失去其自身的物理特性, 导致不同的物理过程表现在同一个IMF分量中, 甚至出现虚假的IMF分量, 影响EMD的精确性[13]。为解决该问题, 郑旭[14]提出MEEMD算法, 在很大程度上抑制了白噪声对原信号的污染, 保证分解结果完备性的同时使得到的各个分量均接近于标准IMF分量。对于信号y(t)的MEEMD分为以下步骤:1)构造的白噪声序列的均方根值应接近于待分解信号的内部噪声, 如果信号内部噪声未知, 则白噪声序列的均方根值不高于待分解信号的0.2倍; 2)在待分解信号y(t)中加入绝对值相等的正负2组白噪声信号a(t), 分解对其进行集总平均次数相等的EEMD; 3)将分解得到的2组IMF分量的对应分量求和取平均值, 最大程度上消除因白噪声产生的残余分量; 4)由于获得的bi(t)并非标准的IMF分量, 需要对其非标准分量进行EMD; 5)得到MEEMD的最终表达式为:
| $ y(t)\mathop \to \limits_{{\rm{MEEMD}}} \sum\limits_{i = 1}^m {\left[ {{c_i}(t)} \right]} + R(t) $ | (1) |
式中, ci(t)为最终的IMF分量, R(t)为最终的残余分量。
综合上述步骤, 本文加入白噪声随机序列, EEMD算法中参考经验公式, 将集总平均次数取值为200次, 分别得到2组8个IMF分量和1个残余分量, 再对分量进行EMD, 得到最终的8个IMF分量及1个总残余分量。
1.2 ERNN模型ERNN是一种典型的动态神经网络, 是在BP人工神经网络基本结构的基础上, 通过内部存储状态使其具备映射动态特征的功能, 从而使网络系统具有适应时变特性的能力。相对于BP神经网络, ERNN除了输入层、隐含层和输出层外, 还增加了一个承接层, 其主要作用是用于层内或层间的反馈联结, 使其能够表达输入与输出之间在时间上的延迟, 可看作是一个延时因子, 需要用动态方程描述, 而前馈神经网络仅仅只能实现非线性映射[15]。ERNN的特点是隐含层的输出通过承接层的延迟与存储自联到隐含层输入, 这种方式使其对历史状态的数据具有更高的敏感性, 提高了网络自身处理动态数据的能力, 达到所需的精度要求。
ERNN非线性状态的空间表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{y}}(k) = g\left( {{\mathit{\boldsymbol{w}}^3}x(k) + {\mathit{\boldsymbol{b}}_2}} \right)}\\ {\mathit{\boldsymbol{x}}(k) = f\left( {{\mathit{\boldsymbol{w}}^1}{x_c}(k) + {\mathit{\boldsymbol{w}}^2}(\mathit{\boldsymbol{u}}(k - 1)) + {\mathit{\boldsymbol{b}}_1}} \right)}\\ {{\mathit{\boldsymbol{x}}_c}(k) = \mathit{\boldsymbol{x}}(k - 1)} \end{array}} \right. $ | (2) |
式中, k为时刻, y、x、u、xc分别为一维输出节点向量、m维隐含层节点单元向量、n维输入向量和m维反馈状态向量, w3、w2、w1分别为隐含层到输出层、输入层到隐含层、承接层到隐含层的连接权值矩阵, b1、b2分别为输入层和隐含层的阈值。
假设第k步系统的实际输出为yd(k), 那么ERNN的目标函数可表示为:
| $ E(k) = \frac{1}{2}{\left( {{\mathit{\boldsymbol{y}}_d}(k) - \mathit{\boldsymbol{y}}(k)} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{y}}_d}(k) - \mathit{\boldsymbol{y}}(k)} \right) $ | (3) |
本文采用3层ERNN模型(即输入层、隐含层、输出层), 最大学习次数设置为迭代5 000次, 预设误差精度为0.001, 并将前20 d的原始数据作为训练数据集, 其中输入层为15 d的数值, 输出层为剩下5 d的数值, 中间15 d的数据作为测试数据集, 最后5 d的数据作为验证数据集, 以此评定网络模型的优劣。隐含层节点数参考以下2个经验公式, 结合实际数据处理过程中的预报效果综合设置为6个节点:
| $ \left\{ {\begin{array}{*{20}{l}} {m = \sqrt {n + l} + a}\\ {m = {{\log }_2}(n)} \end{array}} \right. $ | (4) |
式中, m为隐含层节点数, n为输入层节点数, l为输出层节点数, a为0~10之间的常数。
1.3 MEEMD-ERNN组合模型采用MEEMD-ERNN组合模型进行TEC值的预报, 具体步骤如下:
1) 构造白噪声序列, 利用MEEMD算法对获得的3个不同纬度的TEC数据进行分解, 分别得到8个IMF分量及1个残余分量。
2) 将获得的IMF分量中每月前20 d的IMF分量作为ERNN的训练数据集, 隐含层设置为6层, 最后5 d的IMF分量作为ERNN的验证数据集, 分别对各组数据进行IMF分量的预测, 得到5 d的8个IMF分量和1个残余分量的预测值。
3) 对上一步得到的8个IMF分量和1个残余分量的预测值进行重构, 得到不同纬度多组数据5 d的电离层TEC预测值。
4) 建立对比模型EMD-ERNN组合模型及ERNN模型, 将3种模型得到的预测值与实际值进行对比, 并将均方根误差RMSE、相对精度P及残差百分比Δ作为精度评定指标。
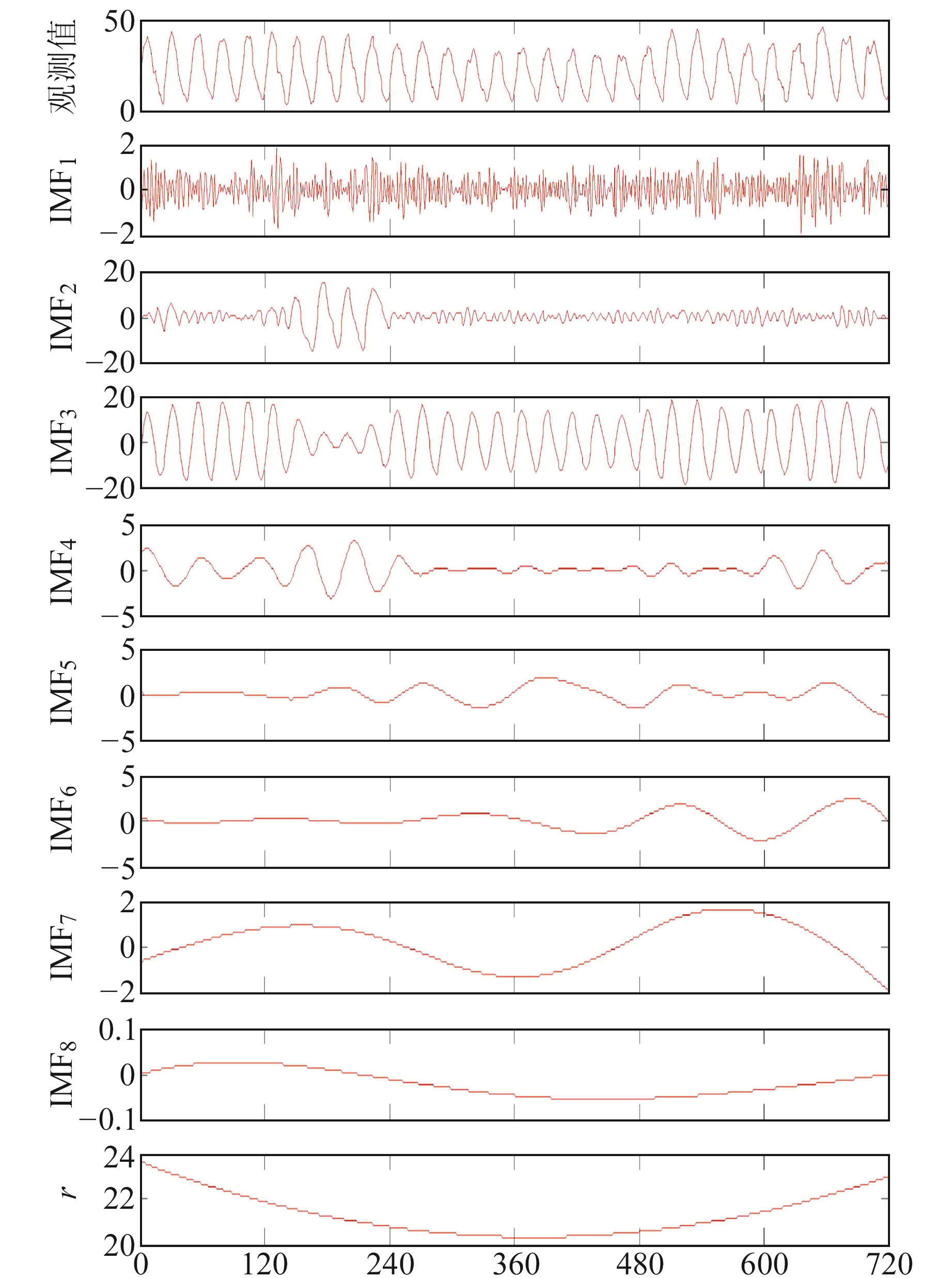
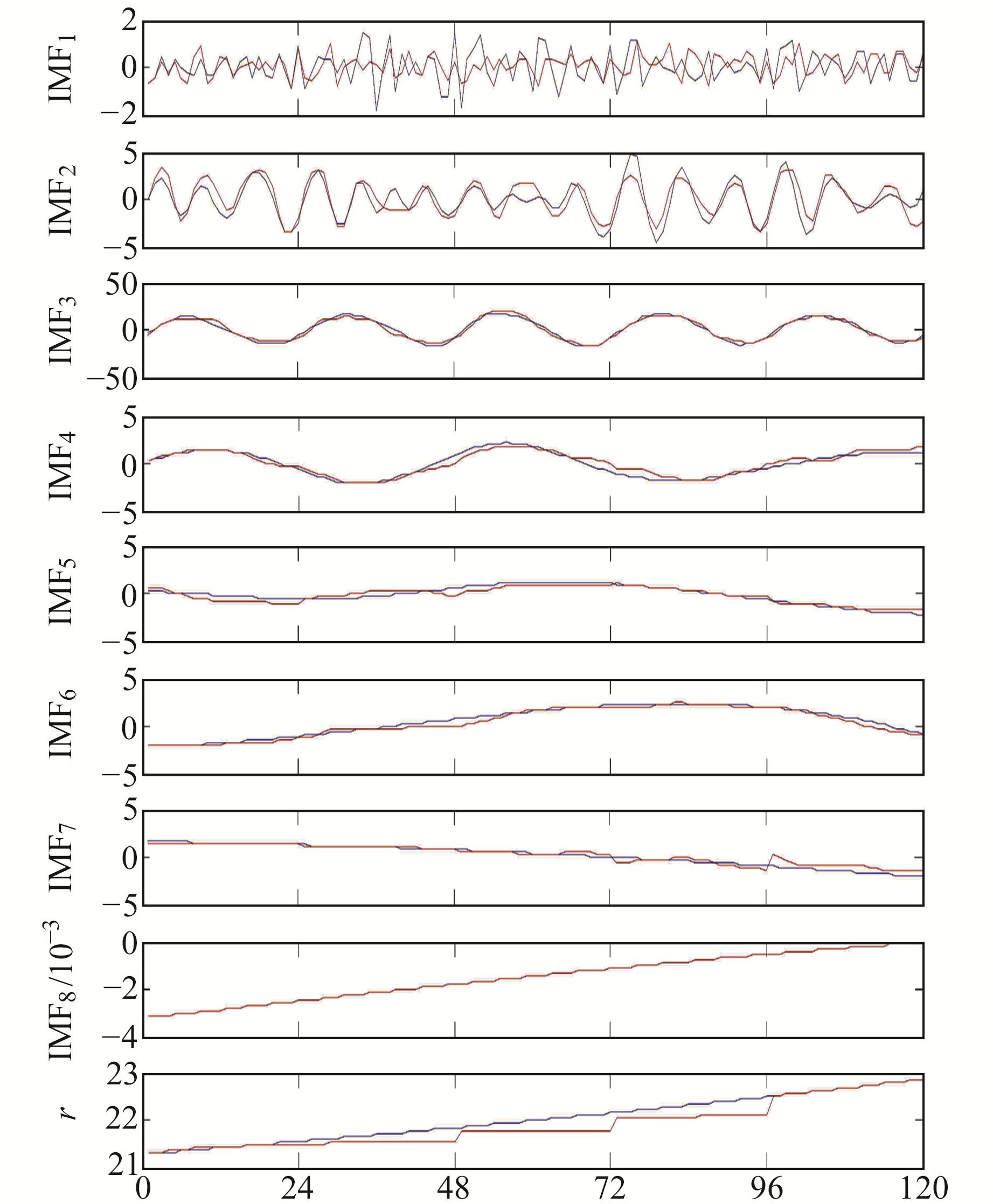
2 实验比较与分析采用IGS中心提供的全球TEC数据对算法进行精度分析, 分别选取2017年年积日60~89、335~364这2个时段内低纬(5°N, 120°E)、中纬(40°N, 120°E)及高纬(75°N, 120°E)地区的TEC数据进行分析。由于篇幅限制, 选取其中1组实验结果进行展示。图 1为低纬(5°N, 120°E)地区年积日60~89的数据分解结果, 经过MEEMD, 8个IMF分量依次由高频到低频特征排列, 与EMD的结果相比, 其更加有效地抑制了模态混叠现象。图 2为经过ERNN预测的年积日85~89的后5 d经验模态分量值。从图中可以看出, 预测的IMF分量与实际分量的差值很小, 预测精度较高。本文利用均方根误差RMSE、相对精度P及残差百分比Δ来评定预报结果的优劣, 即
|
图 1 年积日60~89分解结果 Fig. 1 Decomposition results of doy 60 to 89 |
|
图 2 IMF预测分量与真实分量对比 Fig. 2 Comparison between predicted IMF and original IMF |
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {X_i^p - X_i^0} \right)}^2}} } }\\ {P = 1 - \left| {X_i^p - X_i^0} \right|/X_i^0} \end{array}} \right. $ | (5) |
式中, N为TEC数据的数量, Xip为TEC的预测值, Xi0为实际TEC的值。
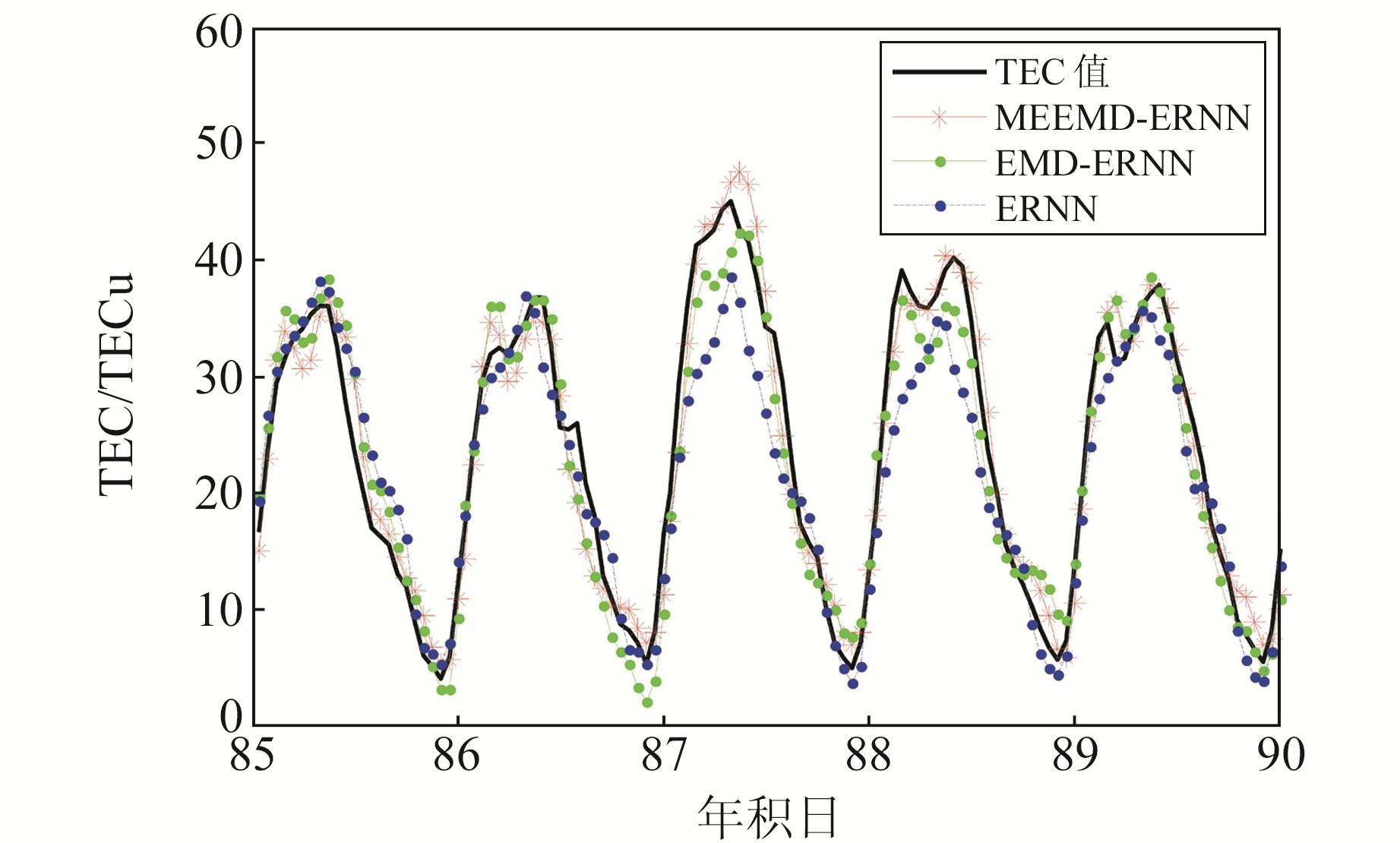
图 3为TEC预报值与实际值的对比, 同时选取MEEMD-ERNN组合模型、EMD-ERNN组合模型和ERNN模型进行比较分析。由图可知, 电离层TEC值在每天都会发生大小不一的数值突变, 出现2个高低峰值, 因此对突变处值的预测质量决定了模型的优劣。EMD-ERNN组合模型与ERNN模型在突变处的预测效果明显低于MEEMD-ERNN组合模型, 且2个模型出现了不同程度的预测极端值, 说明模型在稳定性与精度上产生了失衡, 同时其他时刻MEEMD-ERNN模型的拟合效果也优于另外2个模型。
|
图 3 3种模型预测值与实际值对比 Fig. 3 Comparison between predicted TEC and original TEC by three models |
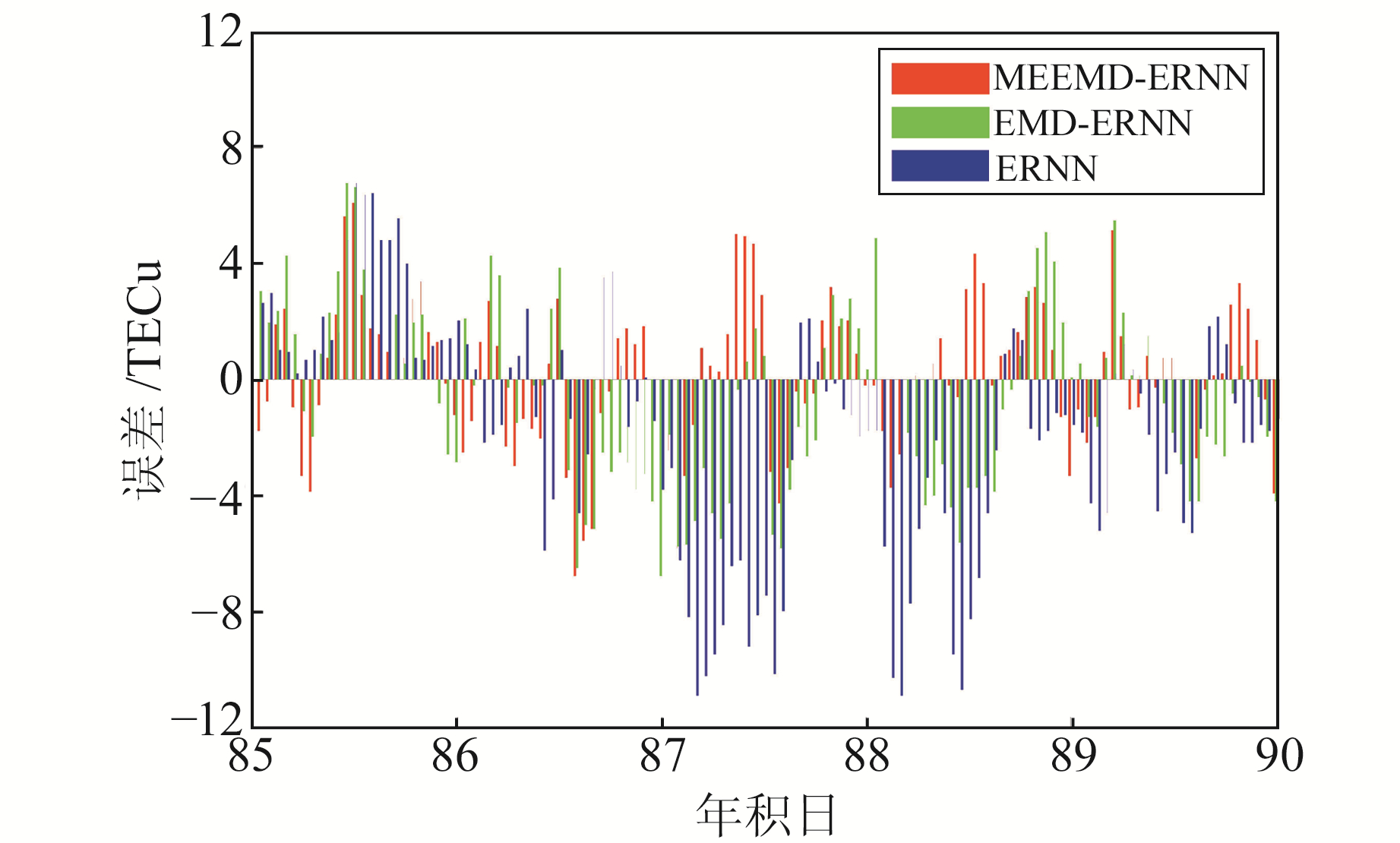
图 4为3种模型TEC实际值与预测值之差。由图可知, MEEMD-ERNN组合模型的预报残差值大部分在2 TECu以内, 最大残差值不超过5 TECu, 且所占比例非常小, 残差值的波动趋势也相对稳定, 说明MEEME-ERNN组合模型的预报精度有显著提高; EMD-ERNN组合模型的预报残差基本都在2~4 TECu以内, 最大残差接近7 TECu, 且占比相对较高, 残差值变化趋势较MEEMD-ERNN组合模型波动较大, 很不稳定; ERNN模型预报残差在4~8 TECu, 是3个模型中误差最大、也是趋势波动最为明显的。由此可知, MEEMD-ERNN组合模型的精度较优, ERNN模型的预报精度较低。
|
图 4 3种模型TEC实际值与预测值之差 Fig. 4 Difference values between predicted TEC and original TEC by three models |
表 1为3种模型在年积日85~89的TEC预测值残差的百分比统计。可以看出, EMD-ERNN组合模型及ERNN模型的预测残差小于1.0 TECu的比例最高分别为29.2%和20.0%, 且预测残差大部分都在2~4 TECu, 误差显著。本文选用的MEEMD-ERNN组合模型的残差值小于1.0 TECu的比例最高为46.0%, 且接近70%的残差值在2 TECu以内, 其他2个模型的比例大约为50%和40%, 因此MEEMD-ERNN组合模型的预测效果明显较优。
|
|
表 1 3种模型TEC预测残差百分比 Tab. 1 Comparison of predicted TEC residual by three models |
表 2为不同纬度下不同年积日的3个模型均方根误差(RMSE)及相对精度P的对比结果。由表可知, MEEMD-ERNN组合模型的预测精度较高, 趋势稳定, 且随着纬度的上升, 整体的预测效果呈上升趋势; EMD-ERNN组合模型与ERNN模型的整体预测精度均低于MEEMD-ERRNN组合模型, 其中EMD-ERNN组合模型误差相对较小。3个模型中, ERNN模型的预测精度变化最为剧烈, 预测数值出现较多的极端值, 由此可见, 经过MEEMD算法预处理的数据可有效提升神经网络模型的稳定性与精确性。EMD-ERNN组合模型虽在稳定度和精度上优于ERNN模型, 但在个别纬度地区的年积日中, EMD-ERNN组合模型也会出现预测稳定性的失衡并出现极端值, 但比ERNN模型少很多。在经过MEEMD处理后, MEEMD-ERNN组合模型有效避免了ERNN模型稳定性失衡的缺点, 预测结果的稳定性得到提高, 最大程度地降低了极端值出现的概率。
|
|
表 2 不同纬度下3个模型预测指标对比 Tab. 2 Comparison of predicted index by three models of different latitudes |
针对电离层TEC值的变化特征存在不平稳、非线性的特性, 本文提出将MEEMD算法与Elman回归神经网络相结合的预测模型, 并与ERNN模型、EMD-ERNN组合模型进行对比。结果表明, MEEMD-ERNN组合模型的预测效果最优。同时, 该组合模型从低纬地区到高纬地区的预报精度较其他2种模型有明显优势, 证明了该方法的可行性和优越性。但由于IGS中心给出的电离层TEC存在一定的偏差, 今后将进一步利用GNSS实测数据估计电离层TEC, 精化区域电离层模型, 并对其进行预报分析。
致谢: 感谢IGS中心提供的GIM数据。
| [1] |
李秀海, 郭达志. 应用半参数AR模型的电离层TEC建模与预测[J]. 测绘科学, 2011, 36(2): 149-151 (Li Xiuhai, Guo Dazhi. Prediction of Ionospheric Total Electron Based on Semiparametric Autoregressive Model[J]. Science of Surveying and Mapping, 2011, 36(2): 149-151)
(  0) 0) |
| [2] |
陈鹏, 姚宜斌, 吴寒. 利用时间序列分析预报电离层TEC[J]. 武汉大学学报:信息科学版, 2011, 36(3): 267-270 (Chen Peng, Yao Yibin, Wu Han. TEC Prediction of Ionosphere Based on Time Series Analysis[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 267-270)
(  0) 0) |
| [3] |
盛峥. 电离层电子总含量不同时间尺度的预报模型研究[J]. 物理学报, 2012, 61(21): 219 401 (Sheng Zheng. Research on Different Time-Scale Prediction Models for the Total Electron Content[J]. Acta Physics Sinica, 2012, 61(21): 219 401)
(  0) 0) |
| [4] |
刘军, 柴洪洲, 刘先冬, 等. 基于ARIMA(p, 1, 1)的电离层预报模型[J]. 大地测量与地球动力学, 2010, 30(3): 79-82 (Liu Jun, Chai Hongzhou, Liu Xiandong, et al. A Predicting Model of Ionospheric Based on ARIMA(p, 1, 1)[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 79-82)
(  0) 0) |
| [5] |
李志刚, 程宗颐, 冯初刚, 等. 电离层预报模型研究[J]. 地球物理学报, 2007, 50(2): 327-337 (Li Zhigang, Cheng Zongyi, Feng Chugang, et al. A Study of Prediction Models for Ionosphere[J]. Chinese Journal of Geophysics, 2007, 50(2): 327-337 DOI:10.3321/j.issn:0001-5733.2007.02.001)
(  0) 0) |
| [6] |
冯炜, 张传定, 吴星, 等. 全球电离层TEC的轮胎调和分析与预报[J]. 测绘学报, 2018, 47(5): 600-610 (Feng Wei, Zhang Chuanding, Wu Xing, et al. Torus Harmonic Analysis and Prediction of Global Ionospheric TEC[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 600-610)
(  0) 0) |
| [7] |
张小红, 任晓东, 吴风波, 等. 震前电离层TEC异常探测新方法[J]. 地球物理学报, 2013, 56(2): 441-449 (Zhang Xiaohong, Ren Xiaodong, Wu Fengbo, et al. A New Method for Detection of Pre-Earthquake Ionospheric Anomalies[J]. Chinese Journal of Geophysics, 2013, 56(2): 441-449)
(  0) 0) |
| [8] |
李淑慧, 彭军还, 徐伟超, 等. 利用神经网络预报短期电离层TEC变化[J]. 测绘科学, 2013, 38(1): 8-9 (Li Shuhui, Peng Junhuai, Xu Weichao, et al. Short-Term Ionospheric TEC Change Prediction by Neural Network[J]. Science of Surveying and Mapping, 2013, 38(1): 8-9)
(  0) 0) |
| [9] |
陆建华, 王斌, 胡伍生. 利用BP神经网络改进电离层短期预报模型[J]. 测绘科学技术学报, 2017, 34(1): 1-4 (Lu Jianhua, Wang Bin, Hu Wusheng. Improved Prediction Models of Ionospheric TEC by BP Neural Network[J]. Journal of Geomatics Science and Technology, 2017, 34(1): 1-4)
(  0) 0) |
| [10] |
汤俊, 姚宜斌, 陈鹏, 等. 利用EMD方法改进电离层TEC预报模型[J]. 武汉大学学报:信息科学版, 2013, 38(4): 408-411 (Tang Jun, Yao Yibin, Chen Peng, et al. Prediction Models of Ionospheric TEC Improved by EMD Method[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 408-411)
(  0) 0) |
| [11] |
吉长东, 王强, 沈祎凡, 等. 自回归神经网络的电离层总电子含量预报[J]. 导航定位学报, 2018, 6(4): 96-101 (Ji Changdong, Wang Qiang, Shen Yifan, et al. TEC Prediction of Ionospheric Based on Nonlinear Auto Regressive Model[J]. Journal of Navigation and Positioning, 2018, 6(4): 96-101)
(  0) 0) |
| [12] |
郑旭, 郝志勇, 金阳, 等. 基于MEEMD的内燃机辐射噪声贡献[J]. 浙江大学学报:工学版, 2012, 46(5): 954-960 (Zheng Xu, Hao Zhiyong, Jin Yang, et al. Studying Noise Contributions of IC Engine via MEEMD Method[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(5): 954-960)
(  0) 0) |
| [13] |
Huang N E, Shen Z, Long S R. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear Non-stationary Time Series Analysis[J]. Proceeding of the Royal Society A: Mathematical Physical and Engineering Sciences, 1998, 454(1 971): 903-995
(  0) 0) |
| [14] |
郑旭.车辆与内燃机振声信号盲分离及噪声源识别的研究[D].杭州: 浙江大学, 2012 (Zheng Xu. Research on Blind Separation and Noise Source Identification for the Vibro-Acoustic Signals of Vehicle and Engine[D]. Hangzhou: Zhejiang University, 2012)
(  0) 0) |
| [15] |
刘荣.基于Elman神经网络的短期负荷预测[D].杭州: 浙江大学, 2013 (Liu Rong. Short-Term Load Forecasting Based on Elman Neural Network[D]. Hangzhou: Zhejiang University, 2013)
(  0) 0) |
2. National Experimental Teaching Demonstration Center of Civil Engineering, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China
 2020, Vol. 40
2020, Vol. 40

