2. 国家自然资源部大地测量数据处理中心, 西安市友谊东路334号, 710054
Hopfield模型[1]和Saastamoinen模型[2]是目前国内最常用的对流层延迟模型, 但两者需要输入气象参数[3]。然而陕西大部分地区缺乏气象数据, 使用受到限制, 无法精确定位, 且不利于陕西地区GNSS研究。UNB系列气象模型[4]的出现摆脱了对气象数据的依赖, 而后根据全球气象参数建立的GPT系列模型[5]可通过全球气象格网快速获得所在区域的气象参数, 且精度较高, 能更好地进行对流层延迟改正。
本文以GAMIT10.7反演出来的对流层延迟ZTD为参考值, 通过MATLAB实现了UNB3m、GPT2w+Hopfield、GPT2w+Saastamoinen、GPT3+Hopfield、GPT3+Saastamoinen(下文中将Saastamoinen简写为Saas, Hopfield简写为Hop)等5种对流层模型, 并对它们进行区域性分析和适用性研究。
1 模型介绍本文只对2018年最新提出的全球气压温度模型GPT2w和GPT3进行简要介绍。Böhm等[6]在GPT2模型的基础上[7], 加入加权平均温度和水汽压递减率, 获得了GPT2w模型, 该模型提供水汽随高程变化相关的参数, 从而提高了较高测站对流层延迟预估的精度。Landskron等[8]计算出修正映射函数VMF3, 并提出一种新的基于全球网格的经验模型GPT3。与GPT2w相比, GPT3新加了一组气象量, 即流体静力北梯度、流体静力东梯度、湿北梯度、湿东梯度。
2 精度评估与分析均匀选取陕西省周边2015~2017年数据完整性较好且有ITRF08框架下的坐标的4个IGS站(LHAZ、URUM、BJFS、SHAO)进行计算。估计策略为:截止高度角为10°, 时间分辨率为2 h, 映射函数采用VMF1, 海潮改正模型为FES2014。将得到的天顶对流层延迟ZTD(分辨率为2 h)与CODE中心发布的高精度天顶对流层延迟ZTD进行比较验证, 通过公式求出两者之间的bias和RMS(表 1)。其中, 因为CODE中心发布的URUM站2017年的ZTD资料较少, 所以不参与比较。由表 1可以看出, 4个IGS站利用GAMIT算出的ZTD与CODE中心发布的ZTD相比较, 平均bias为0.25 mm, 平均RMS为8.18 mm, 精度为mm, 所以可以进行下一步分析。其中, BJFS和URUM站为负向偏差, 而LHAZ和SHAO站为正向偏差, 可能是因为拉萨和上海的气候和地理位置, 导致测站周围空气中水汽含量较高, 所以实测出的ZTD值偏大, 而乌鲁木齐和北京恰好相反。
|
|
表 1 GAMIT-ZTD与CODE-ZTD在不同IGS站的bias和RMS Tab. 1 bias and RMS of GAMIT-ZTD and CODE-ZTD at different IGS stations |
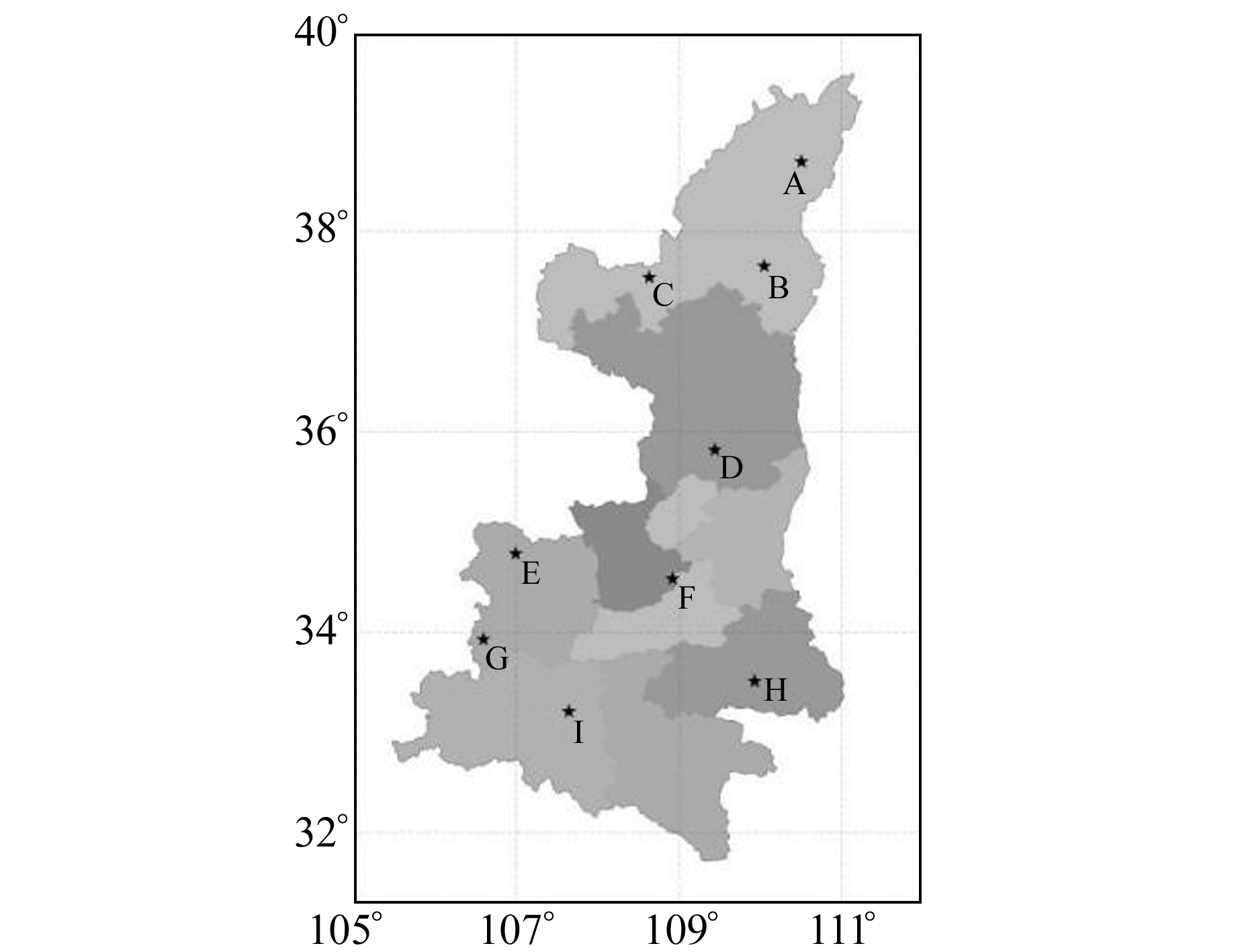
为分析对流层模型在陕西地区的适用性, 使用GAMIT-GLOBK, 以LHAZ、URUM、BJFS、SHAO站为固定站(图 1), 选取陕西区域内9个站为非固定站, 解算出9个站ITRF08框架下的坐标。然后, 分别利用5种策略算出9个站2015~2017年的天顶对流层延迟ZTD(分辨率为2 h), 并与GAMIT解算的各站的天顶对流层延迟ZTD(分辨率为2 h)作比较, 求出两者之间的bias和RMS(表 2)。
|
图 1 GNSS测站在分布 Fig. 1 Distribution of GNSS stations |
|
|
表 2 5种对流层模型bias和RMS Tab. 2 bias and RMS of five tropospheric models |
由表 2可知, 通过模型得到的bias均为负数, 说明在陕西地区利用这5种模型算得的对流层延迟普遍偏小。UNB3m、GPT2w+Hop、GPT3+Hop等3种模型在陕西的精度差异较小, 但精度相对较低, 3 a平均bias均为-6.55 cm, RMS分别为7.50 cm、8.11 cm、8.10 cm。但反观GPT2w+Saas和GPT3+Saas模型在陕西的精度较高, 3 a平均bias为-1.41 cm, RMS分别为4.68 cm、4.67 cm, 并且精度相当, 都适用于陕西地区。比较GPT2w/GPT3+Hop与GPT2w/GPT3+Saas模型发现, 在选用同样的气象参数模型GPT2w或GPT3的情况下, Saas模型比Hop模型更适用于陕西地区。
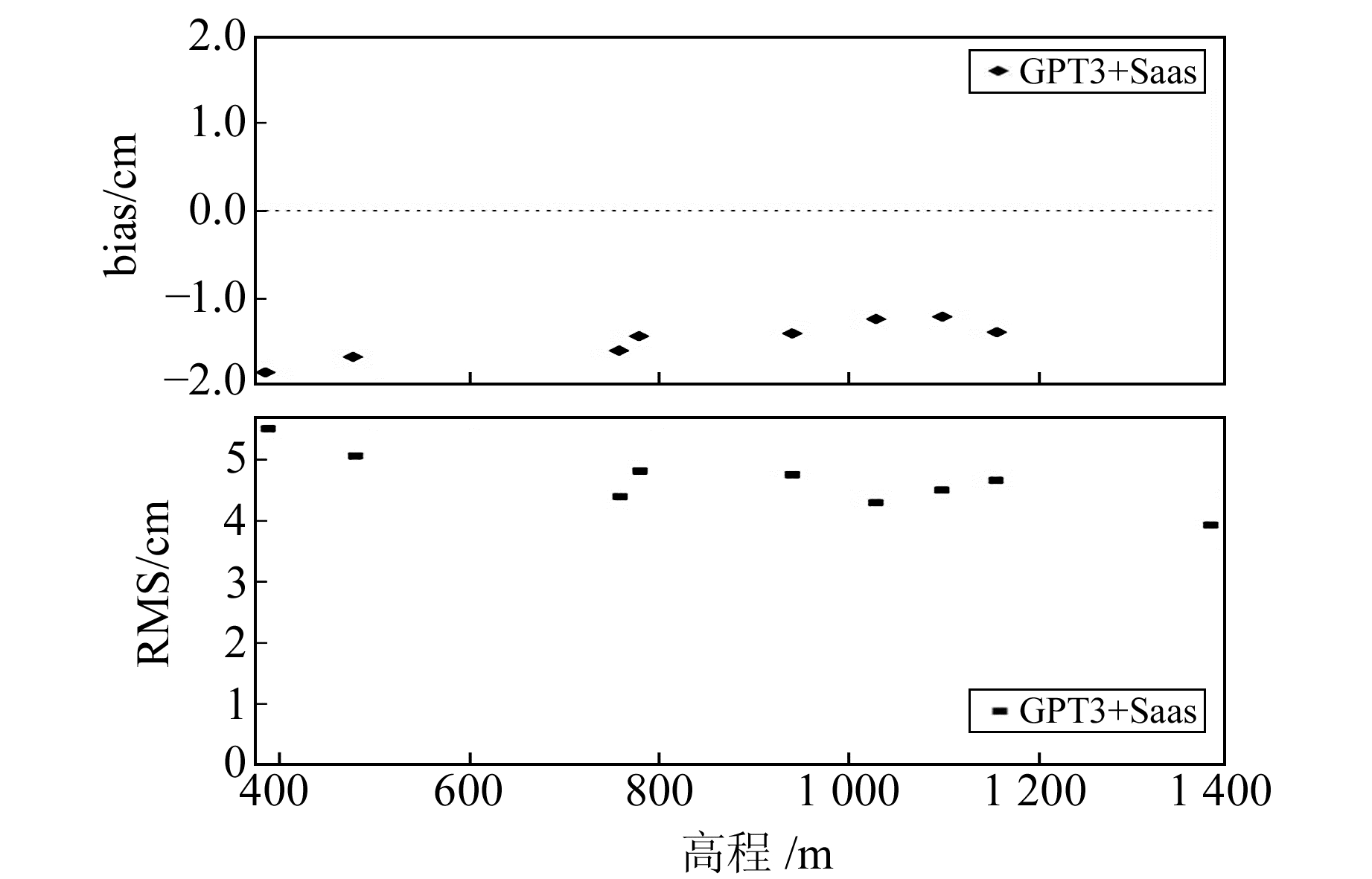
从表 2可以看出, A、B、C、D站计算出的GPT2w/GPT3+Saas模型的bias和RMS均比其余5个测站结果更精确, 因为这4个测站处于陕北的黄土高原地区, 该地区相对干旱、水汽含量较少, 湿延迟变化相对稳定, 所以精度较高。图 2为各测站基于精度最好的GPT3+Saas策略下bias随高程的变化。可以看出, bias和RMS结果整体上随着高程的增加越来越理想, 可能是因为海拔越高, 空气中水汽的含量越少, 继而精度越高。
|
图 2 GPT3+Saas的bias和RMS随着高程的变化 Fig. 2 GPT3+Saas bias and RMS vary with elevation |
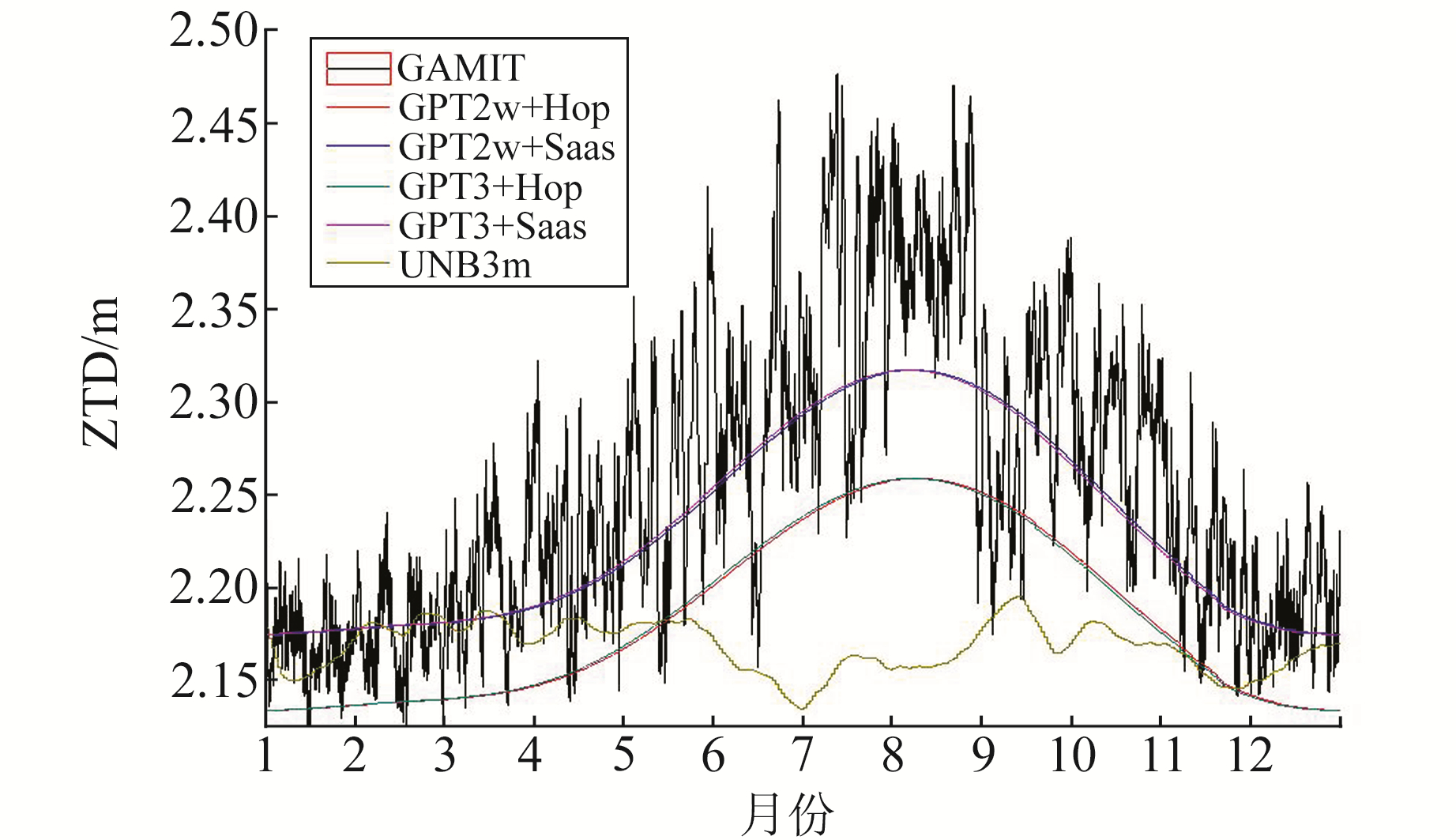
分别用5种模型在春(3~5月)、夏(6~8月)、秋(9~11月)、冬(12~2月)4季解出的ZTD与GAMIT-ZTD估值作对比, 算得bias和RMS。图 3是利用H站2016年不同对流层模型以及GAMIT算得的ZTD时间序列。通过图 3和表 3可知, 5种模型精度均随时间变化而变化, 夏季最低, 冬季最高。陕西地区夏季空气中水汽变化比较剧烈, 使湿延迟变化较大, 最终导致总延迟变化较大; 反观冬季空气较干燥, 湿延迟变化较小, 更易精确求解。其中, UNB3m模型随4季变化最为突出, 夏季和冬季bias差达到7.92 cm, RMS差达到7.67 cm。GPT2w+Hop和GPT3+Hop模型变化也相对较为明显。GPT2w+Saas和GPT3+Saas模型4季的精度最高, 且变化最小。
|
图 3 H站2016年5种模型及GAMIT的ZTD时间序列 Fig. 3 Five computing strategy and GAMIT ZTD time series of H station in 2016 |
|
|
表 3 5种模型在4季的bias和RMS Tab. 3 bias and RMS of five models in four seasons |
以测站I为例, 以月为单位, 统计GPT2w+Saas和GPT3+Saas模型的精度, 将bias绘制成图 4。通过表 3和图 4可以发现, GPT2w和GPT3模型算得的ZTD在冬季精度一致; 春夏2季使用GPT3模型计算ZTD精度略高于GPT2w模型, 但相差不超过1 mm; 秋季选用GPT2w模型能将精度提高1.3 mm。

|
图 4 2种对流层模型I站bias和RMS趋势 Fig. 4 Trend of bias and RMS of two tropospheric models of I station |
想要获得对流层总延迟ZTD与对流层干延迟ZHD, 地面气压(P, 单位hPa)、地面温度(T, 单位℃)、地面水汽压(e, 单位hPa)为必不可少的气象参数。在通过天顶湿延迟ZWD反演大气可降水量PWV时, 必须使用到大气加权平均温度(Tm, 单位K)。分别将GPT2w与GPT3模型算得的地面气压、地面温度、地面水汽压、大气加权平均温度作比较求出bias和RMS(表 4)。从表 2和表 4可以得到, GPT2w或GPT3模型用于对流层总延迟、对流层干延迟及可降水量反演计算时, 整体精度相当。
|
|
表 4 2种模型的bias和RMS Tab. 4 bias and RMS of the two models |
本文利用陕西省9个GNSS观测站2015~2017年的观测数据来比较UNB3m、GPT2w+Hop、GPT2w+Saas、GPT3+Hop、GPT3+Saas等5种对流层模型在陕西地区的精度。结果表明, 5种策略结果均偏小, 精度差异较大, 且都在冬季精度最高, 夏季精度最低。GPT3+Saas和GPT2w+Saas模型全年整体精度相当, 高于其余3种模型, 且受季节变化影响较小, 但在秋季时(9~1月)GPT3+Saas模型精度最高, 而春夏2季时GPT2w+Saas模型精度最高, 随着高程的升高, 精度也有变高的趋势。通过GPT3/GPT2w+Hop模型和GPT3/GPT2w+Saas模型之间的精度对比得出, 在同样气象条件下, Saas模型比Hop模型更适用于陕西地区, 且在陕北地区精度相对最高。UNB3m模型随季节变化精度变化最大, 夏冬2季bias差达到7.92 cm, RMS差达到7.67 cm。如果想要更高的精度, 在秋季时(9~1月)使用GPT3模型, 在春夏2季时使用GPT2w模型, 会得到更高精度的结果。
GPT3与GPT2w模型在陕西地区计算出的地面气压、地面温度、地面水汽压、大气加权平均温度相差不大, 所以将2种模型算出的结果输入同一种对流层延迟模型中, 得到的对流层总延迟ZTD、对流层干延迟ZHD均相近, 并且反演出来的可降水量PWV也几乎一样。
| [1] |
Hopfield H S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357-367 DOI:10.1029/RS006i003p00357
(  0) 0) |
| [2] |
Saastamoinen J. Introduction to Practical Computation of Astronomical Refraction[J]. Bulletin Géodésique, 1972, 106(1): 383-397 DOI:10.1007/BF02522047
(  0) 0) |
| [3] |
张卿川, 李斐, 张胜凯, 等.不同对流层天顶延迟模型在南极半岛地区适用性分析[C].第九届中国卫星导航学术年会, 哈尔滨, 2018 (Zhang Qingchuan, Li Fei, Zhang Shengkai, et al.Applicability Analysis of Different Tropospheric Zenith Delay Models in the Antarctic Peninsula Region[C]. The 9th China Satellite Navigation Conference, Harbin, 2018)
(  0) 0) |
| [4] |
Leandro R, Santos M, Langley R B. UNB Neutral Atmosphere Models: Development and Performance[J]. Proceedings of the National Technical Meeting of the Institute of Navigation NTM, 2006, 52(1): 564-573
(  0) 0) |
| [5] |
Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [6] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [7] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [8] |
Landskron D, Böhm J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions[J]. Journal of Geodesy, 2018, 92(4): 349-360 DOI:10.1007/s00190-017-1066-2
(  0) 0) |
2. Geodetic Data Processing Centre of Ministry of Natural Resources, 334 East-Youyi Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40

