近年来, 微小卫星技术作为新型空间探测技术获得了国际航天领域的广泛关注。然而受成本、能耗和存储资源等方面的限制, 微小卫星上通常搭载单频的GPS接收机来确定卫星的轨道参数。使用单频GPS接收机进行实时定轨可以有效节约成本、降低能耗, 同时观测数据量的减少, 降低了卫星平台数据存储和下传的压力。另一方面, 随着微小卫星技术的快速发展, 在轨微小卫星数量增多、性能增强, 诸多对地观测任务, 如实时监测和快速响应地震和海啸等自然灾害的动态变化等, 对卫星平台轨道参数的实时性和精度提出了更高的要求。基于低成本星载单频GPS观测实现高精度实时自主定轨(星上实时处理)成为近年来星载GPS应用的主要发展趋势之一[1]。
目前, 基于单频星载GPS观测值进行定轨的研究主要集中在事后精密定轨[2-3], 而对于实时精密定轨模型和算法的研究相对较少[4-5]。电离层延迟误差、广播星历误差是限制单频实时定轨精度提高的重要误差源。本文采用L1单频伪距和相位观测值构建GRAPHIC组合, 消除电离层延迟误差的影响, 同时在滤波中为伪模糊度参数设计合理的随机模型, 吸收广播星历轨道和钟差的误差。然后, 利用自主研发的实时精密定轨软件, 采用约化动力学法, 对国内外8颗不同轨道高度低轨卫星的星载GPS实测数据模拟实时定轨解算。最后, 分析本文给出的星载单频GPS实时精密定轨模型和算法的有效性, 详细讨论伪模糊度参数对广播星历误差的吸收效果, 并评估实时定轨结果的精度。
1 星载单频GPS实时定轨数学模型 1.1 观测方程L1载波上伪距和相位观测值的观测方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rho _{{\rm{C}}/{\rm{A}}}} = {\rho _{{\rm{geom}}}} + c\left( {\delta {t_{\rm{r}}} - \delta {t^{\rm{s}}}} \right) + {V_{{\rm{ion}}}} + {\delta _{{\rm{eph}}}} + {\varepsilon _{{\rm{C}}/{\rm{A}}}}}\\ {{\rho _{{\rm{L}}1}} = {\rho _{{\rm{geom}}}} + c\left( {\delta {t_{\rm{r}}} - \delta {t^{\rm{s}}}} \right) - {V_{{\rm{ion}}}} + {\delta _{{\rm{eph}}}} + N + {\varepsilon _{{\rm{L1}}}}} \end{array}} \right. $ | (1) |
式中, 各参数的定义与文献[4]相同。对于单频GPS观测, 可利用同一频率上的伪距和相位观测值电离层延迟误差一阶项大小相等、符号相反的特点, 构建码相无电离层组合(GRAPHIC)观测值, 消除电离层延迟误差一阶项的影响[6]:
| $ \begin{array}{l} \;\;\;\;{\rho _{{\rm{GRAPHIC}}}} = \left( {{\rho _{{\rm{L}}1}} + {\rho _{{\rm{C}}/{\rm{A}}}}} \right)/2 = \\ {\rho _{{\rm{geom}}}} + c\left( {\delta {t_{\rm{r}}} - \delta {t^{\rm{s}}}} \right) + \left( {{\delta _{{\rm{eph}}}} + N/2} \right) + \varepsilon \end{array} $ | (2) |
式中, ρGRAPHIC即为GRAPHIC组合观测值, ε为组合观测值噪声。在忽略载波相位观测值噪声(mm级)的情况下, 组合观测值的噪声仅为C/A码伪距观测值噪声的一半, 则此时限制定轨精度进一步提高的主要误差来源为广播星历误差δeph。如果不顾及δeph的影响, 则该误差中的公共部分会被接收机钟差参数吸收, 不影响实时定轨精度, 而其残余部分不可避免地会进入轨道参数中, 降低实时定轨的轨道精度。另外, 由于δeph参数和模糊度参数均未知, 且无法准确分离, 因此将其合并为一个参数, 称为伪模糊度参数A。
| $ A = {\delta _{{\rm{eph}}}} + N/2 $ | (3) |
其中, 模糊度参数N保持为常数, 因此A的变化与δeph紧密相关。那么理论上, 如果能够根据δeph的变化特性建立参数A的合理随机模型, 准确吸收δeph误差, 就可以有效削弱广播星历误差对实时定轨的影响, 提高星载单频GPS实时定轨精度。
1.2 滤波模型星载GPS实时定轨指以星载GPS跟踪数据为测量值, 结合简易动力学模型, 用拓展卡尔曼滤波估计卫星的状态, 实时获取卫星的位置、速度、姿态等参数, 并提供给星上的其他载荷如姿态控制系统和对地观测数据采集系统, 实现低轨卫星的自主运行[7]。本文单频实时定轨方法以GRAPHIC组合作为主要观测值, 待估向量扩展为:
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{1 \times 3}}}&{{\mathit{\boldsymbol{v}}_{1 \times 3}}}&{{b_u}}&{{{\dot b}_u}}&{{C_D}}&{{C_R}}&{{\mathit{\boldsymbol{\omega }}_{1 \times 3}}}&{{\mathit{\boldsymbol{A}}_{1 \times n}}} \end{array}} \right]^{\rm{T}}} $ | (4) |
式中, r1×3和v1×3为低轨卫星的位置和速度参数, bu=cδtu,
根据前文对伪模糊度参数的分析表明, 如果要通过伪模糊度参数来吸收广播星历误差, 必须设置合适的伪模糊度参数随机模型。Wang等[8]对GPS广播星历误差的研究表明, GPS广播星历误差最大值不超过3 m, 且δeph误差存在缓变特性, 误差变化率约为1.0 mm/s。因此, 本文采用随机游走过程模拟模糊度参数的变化特性:
| $ {A_{k + 1}} = {A_k} + {w_k} $ | (5) |
式中, wk为高斯白噪声, 其方差主要与广播星历误差变化率有关。
2 实验算例及结果分析 2.1 实验数据和定轨方案根据上述单频实时精密定轨模型和算法, 在SATODS软件[7]的基础上, 增加基于星载单频GPS GRAPHIC组合观测值实时定轨功能, 并选取国内外共8颗低轨卫星的实测数据进行星载单频GPS实时定轨性能分析。低轨卫星信息见表 1。
|
|
表 1 低轨卫星及相应的观测值噪声 Tab. 1 Summary of LEO missions and data noise |
为消除电离层延迟误差对实时定轨的影响, 重点验证分析伪模糊度参数随机模型的有效性和星载单频GPS实时精密定轨的性能, 设计2组实时定轨方案:1)采用GRAPHIC组合作为主要观测值, 构建伪模糊度参数吸收广播星历误差, 进行实时定轨解算; 2)使用传统的双频伪距无电离层组合作为主要观测值进行实时定轨解算。2种方案的定轨结果均与事后精密轨道对比, 评估实时定轨的精度。定轨策略设置见表 2, 其中由于CHAMP卫星轨道高度较低, 重力场模型阶数设置为85×85, 其余项所有卫星采用完全相同的数据处理策略。
|
|
表 2 定轨策略设置 Tab. 2 Models and parameters setting of real time orbit determination |
表 3给出了利用2种方案处理表 1中低轨卫星的实测数据的相应定轨结果的位置精度、速度精度(3DRMS)的统计信息, 括号内为径向的位置误差和速度误差。
|
|
表 3 2种实时定轨方案精度分析 Tab. 3 Real-time orbit determination accuracy achievable with different cases |
可以看出, 方案1实时定轨位置精度达到0.44~0.55 m, 远优于方案2的0.75~0.96 m, 精度提升达40%~50%, 可满足一般低轨卫星的实时轨道精度需求。值得注意的是, HY2A和ZY3A两颗搭载国产GPS接收机的低轨卫星的伪距观测值精度相对较差, 双频伪距无电离层组合观测值的噪声达到2 m以上。使用方案2时, ZY3A实时定轨位置精度为0.90 m, HY2A位置精度为0.94 m。而使用方案1, 定轨精度有大幅度提高, ZY3A和HY2A位置精度达到0.52 m和0.44 m。可见, 即使伪距观测噪声较大, 使用GRAPHIC组合观测值实时定轨仍可以获得较高精度的轨道。
进一步分析2种方案自主定轨结果的误差变化情况, 图 1给出了GRACE-A卫星2006年doy=200和HY2A卫星2012年doy=003时使用2种方案的轨道误差曲线。可以发现, 对于GRACE-A卫星, 方案2传统双频伪距实时定轨结果的径向误差范围为±0.75 m, 切向误差范围为±1.8 m, 法向误差范围为±0.5 m, 位置的3D误差可达2.0 m; 而使用方案1时, GRAPHIC组合观测值实时定轨结果的3个方向的误差依次优于±0.3、±1.0 m和±0.3 m, 3D位置误差优于1.1 m, 对于HY2A卫星有类似的精度情况。从误差曲线可以看出, 使用GRAPHIC组合观测值的实时定轨, 其结果在径向、切向、法向上的精度均有明显提高, 且在径向和切向方向上提高程度较大。

|
图 1 GRACE-A和HY2A卫星2种方案实时定轨位置误差 Fig. 1 GRACE-A and HY2A real-time orbit determination results of cases 1 and 2 |
无论低轨卫星轨道的高低, 使用GRAPHIC组合观测值都可以获得更高精度的定轨结果。分析其原因为:1)GRAPHIC组合有效消除了电离层延迟误差一阶项的影响; 2)组合观测值的噪声远小于双频伪距无电离层组合观测值的噪声, 理论上约为其1/6;3)该方法构建GRAPHIC组合使用相位观测值, 通过对伪模糊度参数设置合理的随机模型, 吸收了广播星历沿信号传播方向上的误差, 从而提高了实时定轨的精度。
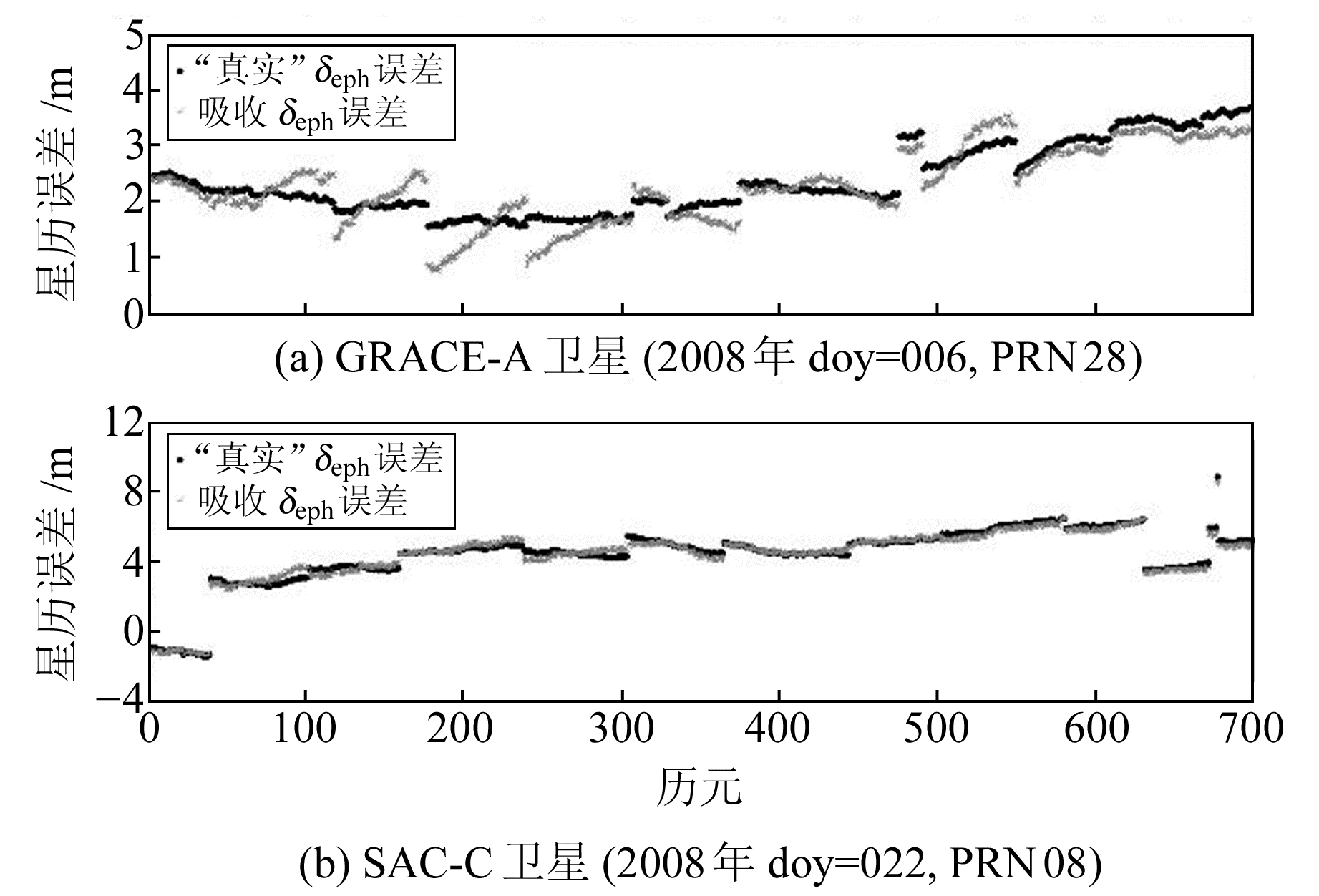
2.3 模糊度参数误差吸收效果分析根据前面的分析, 伪模糊度参数对GPS广播星历误差的吸收是星载单频GPS实时定轨精度提高的重要原因, 下面将重点对伪模糊参数的误差吸收效果进行分析。图 2(a)给出了GRACE-A卫星在2008年doy=006实时定轨期间GPS PRN28卫星的广播星历轨道、钟差误差沿信号传播方向的投影, 图 2(b)给出了SAC-C卫星在2008年doy=022实时定轨期间GPS PRN08卫星的广播星历误差沿信号传播方向的投影, 忽略其中GPS卫星不可通视的弧段。图中, “·”代表使用广播星历计算GPS卫星的位置和钟差参数与IGS发布的最终产品计算的GPS卫星位置和钟差(精度优于5 cm)的差异在信号传播方向上的投影, 称为“真实”δeph误差, 可参考文献[9]计算得到; “*”表示伪模糊度参数吸收的δeph误差, 即伪模糊度参数减去真实的模糊度参数之后的残余项。其中伪模糊度参数通过前面的滤波模型估计给出, 真实的模糊度参数通过使用IGS发布的高精度轨道和钟差产品进行事后精密定轨给出。
|
图 2 GRACE-A和SAC-C卫星单天星历误差与伪模糊度吸收误差 Fig. 2 Ephemeris errors caused by the broadcast ephemeris and estimated in the pseudo-ambiguity for GRACE-A and SAC-C |
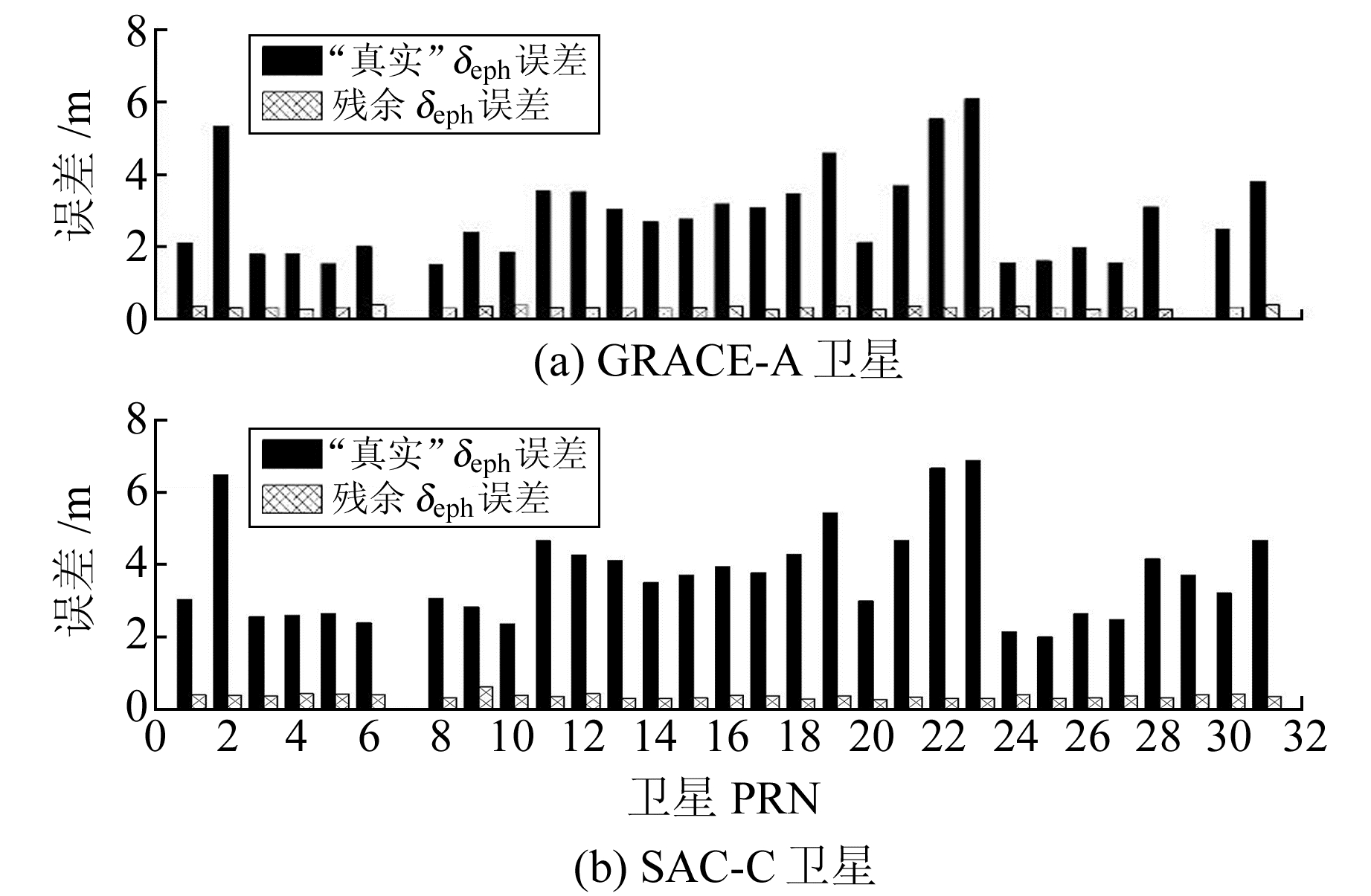
从图 2中可以看到, 2条曲线的走向基本一致, 说明使用本文GRAPHIC组合构建的伪模糊度参数可以有效吸收广播星历轨道和钟差在信号传播方向上的误差分量。图 3给出了GRACE-A卫星和SAC-C卫星在整个定轨时段(30 d)使用方案1实时定轨时每颗观测到的GPS卫星对应的“真实”δeph误差的RMS以及伪模糊度参数吸收后的残余δeph误差的RMS的统计信息。可以发现, 构建伪模糊度参数后, 对于所有的可观测GPS卫星, 误差吸收后残余误差RMS均不超过0.4 m。对于GRACE-A卫星, 整体残余的传播路径上的误差的RMS为0.31 m; 对于SAC-C卫星整体残余误差为0.33 m。
|
图 3 “真实”δeph误差与残余星历误差统计 Fig. 3 RMS comparison of "true" and residual ephemeris errors |
模糊度参数吸收的误差与广播星历卫星视线误差变化的曲线基本吻合。经过模糊度参数吸收之后的广播星历残余误差在0.30 m左右, 远小于广播星历的误差。说明模糊度参数有效吸收了广播星历中卫星轨道和钟差误差, 是单频实时定轨获得更高精度的主要原因。而一般来说, 星载GPS观测的PDOP值通常为1.5~2.5, 由此可以推断方案1的实时定轨精度为0.45~0.75 m, 这与表 3的精度统计也相吻合。
3 结语本文使用星载单频GPS构建GRAPHIC组合作为主要观测值, 根据GPS卫星星历误差特性为伪模糊度参数设计合理的随机模型, 用来吸收GPS广播星历轨道和钟差误差, 实现基于单频GPS观测的高精度实时定轨。通过模拟在轨实时处理轨道高度320~1 350 km的8颗低轨卫星的实测数据, 可以得出以下结论:
1) 使用GRAPHIC组合观测值实时定轨, 可以得到0.44~0.55 m的位置精度, 0.37~0.63 mm/s的速度精度, 且定轨精度与卫星轨道高度的分布并无明显相关性。相对于传统的基于双频伪距观测值的实时定轨结果, 精度提高40%左右。
2) ZY3-A和HY2-A卫星搭载国产GPS接收机, 虽然伪距观测值噪声较大, 但是使用GRAPHIC组合观测值实时定轨仍然能获得0.52 m和0.44 m的位置精度。
3) 伪模糊度参数误差吸收效果分析表明, 该参数可以有效吸收广播星历中轨道和钟差误差, 吸收后星历残余误差约为0.3 m, 这是星载单频GPS实时定轨轨道精度提高的本质原因。
根据本文结果, LEO卫星仅搭载低成本的单频GPS接收机, 即可以实时获得亚米级精度的轨道参数, 对于我国未来低成本的空间探测计划具有一定的参考意义。另外, 由于增加了伪模糊度参数, 待估状态向量维数扩大, 计算复杂度增加, 因此下一步有必要验证该方法在星载平台上实时自主运行的可行性。
| [1] |
Yunck T P. The Promise of Spaceborne GPS for Earth Remote Sensing[C]. International Workshop on GPS Meteorology, Japan, 2003
(  0) 0) |
| [2] |
Bock H, Jäggi A, Dach R, et al. GPS Single-Frequency Orbit Determination for Low Earth Orbiting Satellites[J]. Advances in Space Research, 2009, 43(5): 783-791 DOI:10.1016/j.asr.2008.12.003
(  0) 0) |
| [3] |
郭向, 张强, 赵齐乐, 等. 基于单频星载GPS数据的低轨卫星精密定轨[J]. 中国空间科学技术, 2013, 33(2): 41-46 (Guo Xiang, Zhang Qiang, Zhao Qile, et al. Precise Orbit Determination for LEO Satellites Using Single-Frequency GPS Observations[J]. Chinese Space Science and Technology, 2013, 33(2): 41-46)
(  0) 0) |
| [4] |
王甫红, 郭磊, 邵晓东, 等. 两种电离层延迟改正模型对星载单频GPS实时定轨精度的影响[J]. 大地测量与地球动力学, 2016, 36(7): 565-569 (Wang Fuhong, Guo Lei, Shao Xiaodong, et al. Effects Analysis of Two Ionosphere Correction Models on Space-Borne GPS Single-Frequency Real-Time Orbit Determination[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 565-569)
(  0) 0) |
| [5] |
Montenbruck O, Swatschina P, Markgraf M, et al. Precision Spacecraft Navigation Using a Low-Cost GPS Receiver[J]. GPS Solutions, 2012, 16(4): 519-529 DOI:10.1007/s10291-011-0252-6
(  0) 0) |
| [6] |
Montenbruck O. Kinematic GPS Positioning of LEO Satellites Using Ionosphere-Free Single Frequency Measurements[J]. Aerospace Science and Technology, 2003, 7(5): 396-405 DOI:10.1016/S1270-9638(03)00034-8
(  0) 0) |
| [7] |
王甫红.星载GPS自主定轨理论及其软件实现[D].武汉: 武汉大学, 2006 (Wang Fuhong. Theory and Software Development on Autonomous Orbit Determination with Spaceborne GPS Measurements[D]. Wuhan: Wuhan University, 2006)
(  0) 0) |
| [8] |
Wang F H, Gong X W, Sang J Z, et al. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver[J]. Sensors, 2015, 15(12): 30 403-30 418 DOI:10.3390/s151229805
(  0) 0) |
| [9] |
王甫红, 龚学文, 刘万科. 顾及广播星历误差分离吸收的分米级星载GPS实时定轨新方法[J]. 武汉大学学报:信息科学版, 2015, 40(9): 1 230-1 236 (Wang Fuhong, Gong Xuewen, Liu Wanke. A Novel Decimeter-Level Real-Time Orbit Determination Algorithm Using Space-Borne GPS Measurements with Separation and Absorption of Broadcast Ephemeris Error[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1 230-1 236)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

