2. 武汉地震工程研究院有限公司,武汉市洪山侧路40号,430071
我国绝大多数油田属于陆相湖盆碎屑岩沉积,薄互层储层发育,储层的强非均质性和复杂的地震波响应严重影响薄互层油藏的勘探成功率[1]。传统的AVO(amplitude variation with offset)反演基于L2范数,其假设地下地层为光滑模型,该假设限制了薄互层油气藏的识别研究。由于地下介质可以假设为由块状结构构成,其反射系数可看作是稀疏分布,因此可在稀疏性的假设条件下进行反射系数的反演。压缩感知稀疏信号采样和重构理论表明,在一定的假设条件下,可从有限带宽的地震资料中反演出稀疏的脉冲状反射系数。反射系数的稀疏反演在压缩感知稀疏信号采样和重构理论下可表示为零范数下的反演问题,但由于零范数的求解通常采用贪婪算法,且容易陷入局部极值,对噪声比较敏感,计算量巨大。对于上述问题,一般采用L1范数约束来获得近似零范数的近似解。对于压缩感知框架下的L1范数优化问题,首先将高度非线性化的L1优化问题转化为线性规划问题,然后结合原对偶对数障碍法,采用求解大型线性规划问题的基追踪算法求解矩阵方程组。通过基于压缩感知原理的L1范数约束下的AVO反演,得到地下稀疏的尖脉冲状反射系数,由于薄互层也可表示为有限反射系数响应的叠加,故反演可提高薄互层的分辨率和反演精度[2]。L1范数约束下的AVO反演首先需要建立表示反射率模式的函数字典,地震数据可由这些模式的叠加与子波的褶积来表示;然后采用基追踪算法求解L1范数约束下的反演问题,通过反演得到稀疏表示的地下脉冲状反射系数;最后将反演得到的反射系数与构建的反射率模式字典褶积,即可得到稀疏的反演结果[3]。如果已知初始模型,利用L1范数约束下的AVO反演得到的反射系数,可以确定宽带的地震阻抗模型[4]。
本文首先阐述了压缩感知框架下基于L1范数的AVO反演理论基础,然后采用典型的楔形体模型对该算法的精度及其抗噪性进行测试,最后采用传统的AVO反演算法及本文的反演算法对实际资料进行反演测试,并与测井数据进行对比。
1 理论基础 1.1 AVO反演方程Zoeppritz方程描述了入射角、地下介质参数和反射系数之间的关系,但该方程求取复杂,可利用波速而非反射系数作为参数:
| $ {{{r}}_{\rm{ \mathit{ θ} }}} = \frac{{{{\sec }^2}{\rm{ \mathit{ θ} }}}}{2}{\gamma _{\rm P} } - 4{\bar \gamma ^2}{\sin ^2}{\rm{ \mathit{ θ} }}{\gamma _{\rm S}} + \frac{1}{2}\left( {1 - 4{{\sin }^2}{\rm{ \mathit{ θ} }}{{\bar \gamma }^2}} \right){\gamma _d} $ | (1) |
式中,
| $ {R_{\rho \rho }}\left( \theta \right) = a\left( \theta \right){R_{\rm P}} + b\left( \theta \right){R_{\rm S}} + c(\theta ){R_d} $ | (2) |
式中, RP、RS、Rd分别为纵波、横波和密度反射系数。若在每一个时间样本t中将式(2)转化成向量形式,对于N个入射角,可以写为:
| $ \begin{array}{c} \left[ {\begin{array}{*{20}{c}} {{R_{\rho \rho }}\left( {t, {\theta _1}} \right)}\\ {{R_{\rho \rho }}\left( {t, {\theta _2}} \right)}\\ \vdots \\ {{R_{\rho \rho }}(t, {\theta _N})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_{\rm P}}\left( {t, {\theta _1}} \right), {C_{\rm S}}\left( {t, {\theta _1}} \right), {C_\rho }\left( {t, {\theta _1}} \right)}\\ \vdots \\ {{C_{\rm P}}\left( {t, {\theta _N}} \right), {C_{\rm S}}\left( {t, {\theta _N}} \right), {C_\rho }(t, {\theta _N})} \end{array}} \right] \cdot \\ {\left[ {{R_{\rm P}}\left( t \right), {R_{\rm S}}\left( t \right), {R_\rho }(t)} \right]^{\rm T}} \end{array} $ | (3) |
式中, CP、CS、Cρ分别为线性近似系数, RP(t)、RS(t)、Rρ(t)分别为反射系数序列。将式(3)两边同时与子波褶积,可以得到角道集与一个子波矩阵,褶积运算之后得到:
| $ \begin{array}{c} \left[ {\begin{array}{*{20}{c}} {{S_{\rho\rho}}\left( {t, {\theta _1}} \right)}\\ {{S_{\rho\rho}}\left( {t, {\theta _2}} \right)}\\ \vdots \\ {{S_{\rho\rho}}(t, {\theta _N})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{ \boldsymbol{W}_{\rm P}}\left( {t, {\theta _1}} \right), {\boldsymbol{W}_{\rm S}}\left( {t, {\theta _2}} \right), {\boldsymbol{W}_\rho }\left( {t, {\theta _3}} \right)}\\ \vdots \\ {{\boldsymbol{W}_{\rm P}}\left( {t, {\theta _N}} \right), {\boldsymbol{W}_{\rm S}}\left( {t, {\theta _N}} \right), {\boldsymbol{W}_\rho }(t, {\theta _N})} \end{array}} \right] \cdot \\ {\left[ {{R_{\rm P}}\left( t \right), {R_{\rm S}}\left( t \right), {R_\rho }(t)} \right]^{\rm T}} \end{array} $ | (4) |
式(4)的简单形式可以写成:d = Gm。其中,Sρρ为叠前角道集,对应d,W为子波矩阵,对应G,R为反射系数,对应m。由此可为建立目标函数:
| $ \min \left[ {\parallel \boldsymbol{d} - \boldsymbol{Gm}{\parallel _2} + \lambda \parallel \boldsymbol{m}{\parallel _1}} \right] $ | (5) |
式中,λ为影响方程稀疏度的正则化参数。根据式(5)通过对模型的L1范数约束对储层进行稀疏脉冲反演,可以得到相应的稀疏状反射系数,具体求解算法在下文中阐述。
1.2 L1范数AVO反演算法L1范数的理论基础源于压缩感知理论[6]:如果某一信号在正交空间是稀疏的,或者是可压缩的,那么即可以比较低的频率对信号采样并重新构建这个信号。式(6)为压缩感知原理的理论数学模型,将实信号x在某组正交基{φi}iN=1下展开[7]:
| $ x = \sum\limits_{i = 1}^N {{\theta _i}{\psi _i}} $ | (6) |
式中,θi < x, ψi≥x。将式(6)表示为矩阵形式:x = θψ,ψ为正交基字典矩阵,θ为展开系数向量,为K-系数的。首先用一个与正交基字典没有关联的观测矩阵φ对信号x执行压缩观测,得到y = xφ,y为M个线性投影[8]。
当满足压缩信号是稀疏的,且求得的系数向量在正交基空间中是K-系数的,就可以通过式(7)求得x [9]:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\min }_\theta } = \parallel \boldsymbol{\theta} {\parallel _0}}\\ { \boldsymbol{y} = \boldsymbol{\psi \theta \varphi} } \end{array}} \right. $ | (7) |
零范数较难求解,可用L1范数下的凸化压缩感知恢复框架:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\min }_\theta } = \parallel \boldsymbol{\theta} {\parallel _1}}\\ { \boldsymbol{y} = \boldsymbol{\psi \theta \varphi} } \end{array}} \right. $ | (8) |
将L1范数理论运用在AVO反演中,首先需要解决薄互层反演精度不高的问题,因为薄互层可以表示为稀疏层的组合;其次该算法需具有一定的抗噪性,如果其对噪声非常敏感,那么在实际应用中是不可取的。下面主要介绍基于L1范数的AVO反演策略。
首先建构一系列不同厚度的对称和不对称的奇偶脉冲对[10],可依据地质先验信息、地震数据的采样间隔等进行建构。然后将纵横波速度、密度对应的不同厚度的奇偶脉冲对构成地层响应楔形字典G。假设一个薄互层的顶底反射系数为c、d, 反射率脉冲对用δ(t)和δ(t+Δt)表示,其中Δt为采样速率,用nΔt表示薄互层的厚度,通过奇偶分解来建构反射系数奇偶脉冲对γe、γo:
| $ \left\{ \begin{matrix} \begin{array}{l} {{\gamma }_{e}}=\delta \left( t \right)+\delta \left( t+n\Delta t \right) \\ {{\gamma }_{o}}=\delta \left( t \right)-\delta \left( t+n\Delta t \right) \\ c\delta \left( t \right)+d\delta \left( t+n\Delta t \right)={{a}_{e}} \cdot {{\gamma }_{e}}+{{b}_{o}}\cdot{{\gamma }_{o}} \\ \end{array} \end{matrix} \right. $ | (9) |
式中,ae、bo分别为反射系数对应的奇偶分解对。通过此算法,可以将反射系数RP(t)、RS(t)、Rρ(t)表示为奇偶分解的矩阵形式,代入式(6),得到由小波矩阵和楔形反射率矩阵相乘得到的新矩阵。根据这种分解,任何角道集都可以由楔形地震和建模得到,然后用ae、bo来计算反射系数序列。得到反射系数序列后,将其近似地表示成纵横波速度和密度的导数形式[11]:
| $ \left\{ {\begin{array}{*{20}{l}} {{{{R}}_{\rm{S}}}\left( {{t}} \right) = \frac{{\Delta {{{V}}_{\rm{S}}}}}{{{{{{\bar V}}}_{\rm S}}}}\frac{\partial }{{\partial {{t}}}}{\rm{ln}}{{{V}}_{\rm{S}}}\left( {{t}} \right)}\\ {{{{R}}_{\rm{P}}}\left( {{t}} \right) = \frac{{\Delta {{{V}}_{\rm P}}}}{{{{{{\bar V}}}_{\rm P}}}}\frac{\partial }{{\partial {{t}}}}{\rm{ln}}{{{V}}_{\rm{P}}}\left( {{t}} \right)}\\ {{{{R}}_{{\rm{ }}\rho {\rm{ }}}} = \frac{{\Delta {\rho _t}}}{{{{\bar \rho }_t}}}\frac{\partial }{{\partial {{t}}}}{\rm{ln }}\rho {{\rm{ }}_{{t}}}} \end{array}} \right. $ | (10) |
对两边同时进行积分:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{ln}}{V_{\rm{S}}}\left( {{t}} \right) = \int_{\rm{S}}^R {\left( t \right){\rm{d}}t + {\rm{ln}}{V_{{{\rm{S}}_0}}}\left( t \right)} }\\ {{\rm{ln}}{V_{\rm{P}}}\left( {{t}} \right) = \int_{\rm{P}}^R {\left( t \right){\rm{d}}t + {\rm{ln}}{V_{{\rm{P}}_0}}\left( t \right)} }\\ {{\rm{ln}}\rho \left( {{t}} \right) = \int_\rho ^R {\left( t \right){\rm{d}}t + {\rm{ln}}{\rho _0}\left( t \right)} } \end{array}} \right. $ | (11) |
式中,VS0、VP0、ρ0分别为初始纵横波速度和密度模型,通常由测井数据低通滤波后得到。最后两边取对数求得相应的纵横波速度和密度值。传统AVO反演输出的结果相对平滑,基于L1范数的AVO反演输出的结果为不带子波效应的脉冲状反射系数,然后通过初始模型进一步获得地下介质参数。
2 模型反演 2.1 合成地震记录L1范数反演理论测试前文已阐述基于L1范数进行AVO反演的理论基础,将子波矩阵、叠前角道集以及反射系数通过式(5)建立相应的目标泛函。实际上,无论在传统的AVO反演还是基于L1范数的AVO反演中,影响反演结果的除了地震子波、数据质量等因素,还包括权重因子λ。λ为反演稀疏度的正则化参数,其值的选取十分重要。下面采用理论模型探讨不同λ取值对有/无噪声数据反演结果的影响。
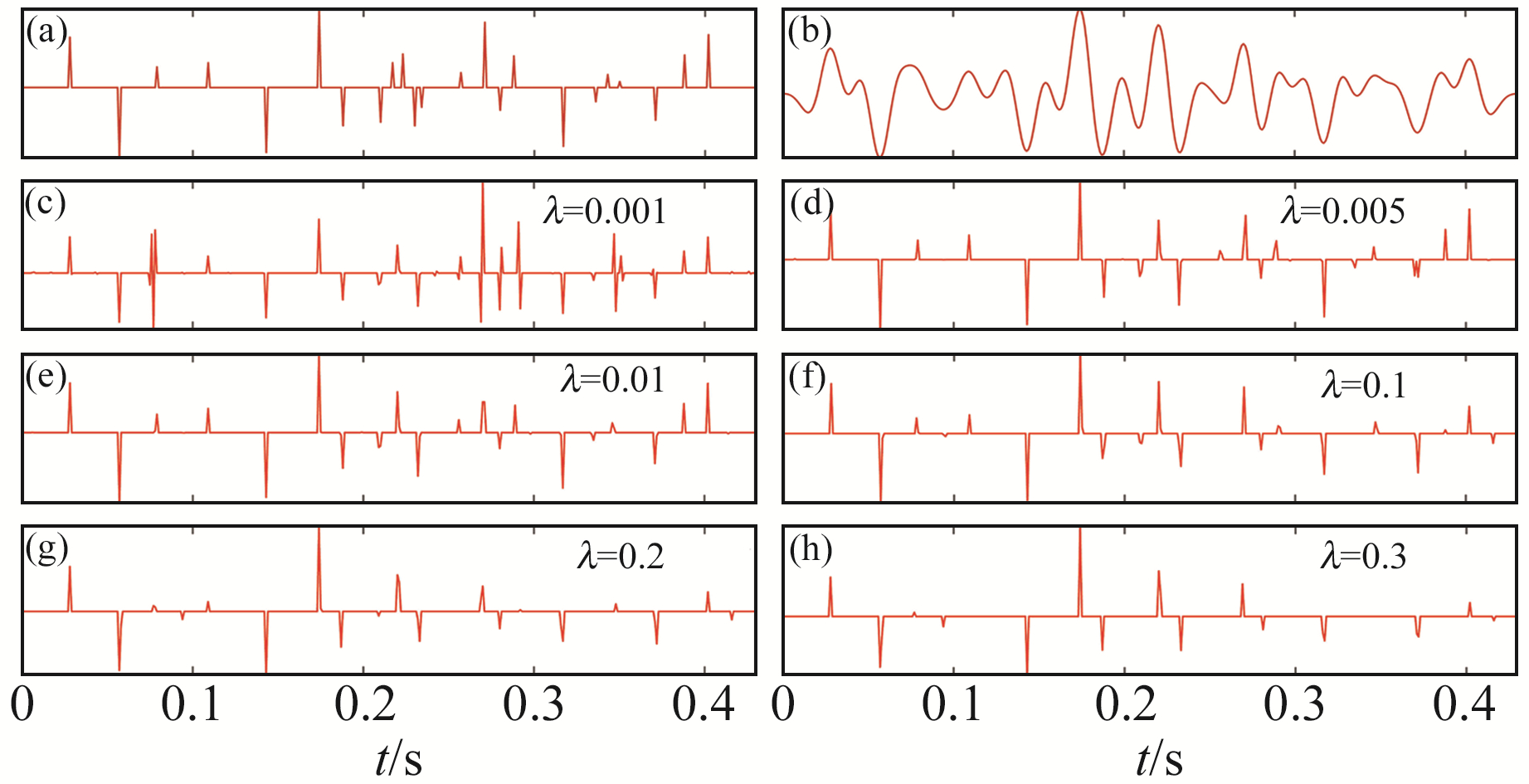
图 1为无噪声情况下不同λ值得到的反演结果,其中,图 1(a)为采样间隔1 ms,幅值在-0.29~0.26之间的反射系数序列;图 1(b)为反射系数序列与频率30 Hz的雷克子波卷积得到的合成记录;图 1(c)~(h)表示取不同的λ值对应的L1范数的反演结果。对比发现,当λ值过小时,反演得到的反射系数密集;当λ值偏大时,反演结果稀疏;λ取0.01左右效果较好。
|
图 1 无噪声情况下不同λ值的反演结果 Fig. 1 Inversion results of different λ values without noise |
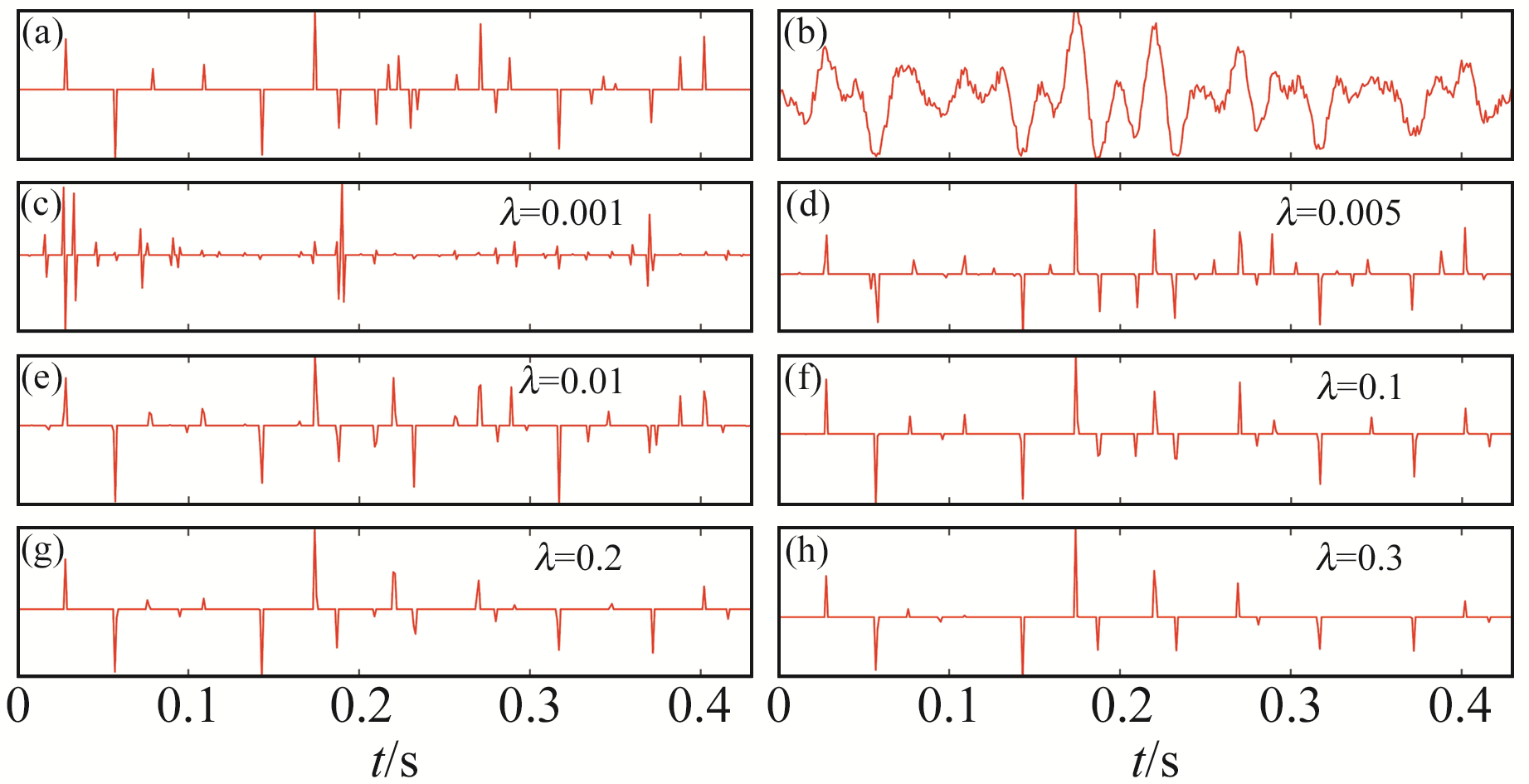
图 2为加入10%噪音后的不同λ值反演结果,其中,图 2(a)为采样间隔1 ms,幅值在-0.29~0.26之间的反射系数序列;图 2(b)为反射系数序列与频率30 Hz的雷克子波卷积并加入10%随机噪声得到的合成地震记录;图 2(c)~(h)表示取不同的λ值对应的L1范数反演结果。对比发现,不同λ取值得到的结果与不加噪声数据得到的反演结果类似,但是λ的最优取值较不加噪声时要大,同时反演结果较好。
|
图 2 加入10%随机噪声后L1反演结果 Fig. 2 L1 inversion results after adding 10% random noise |
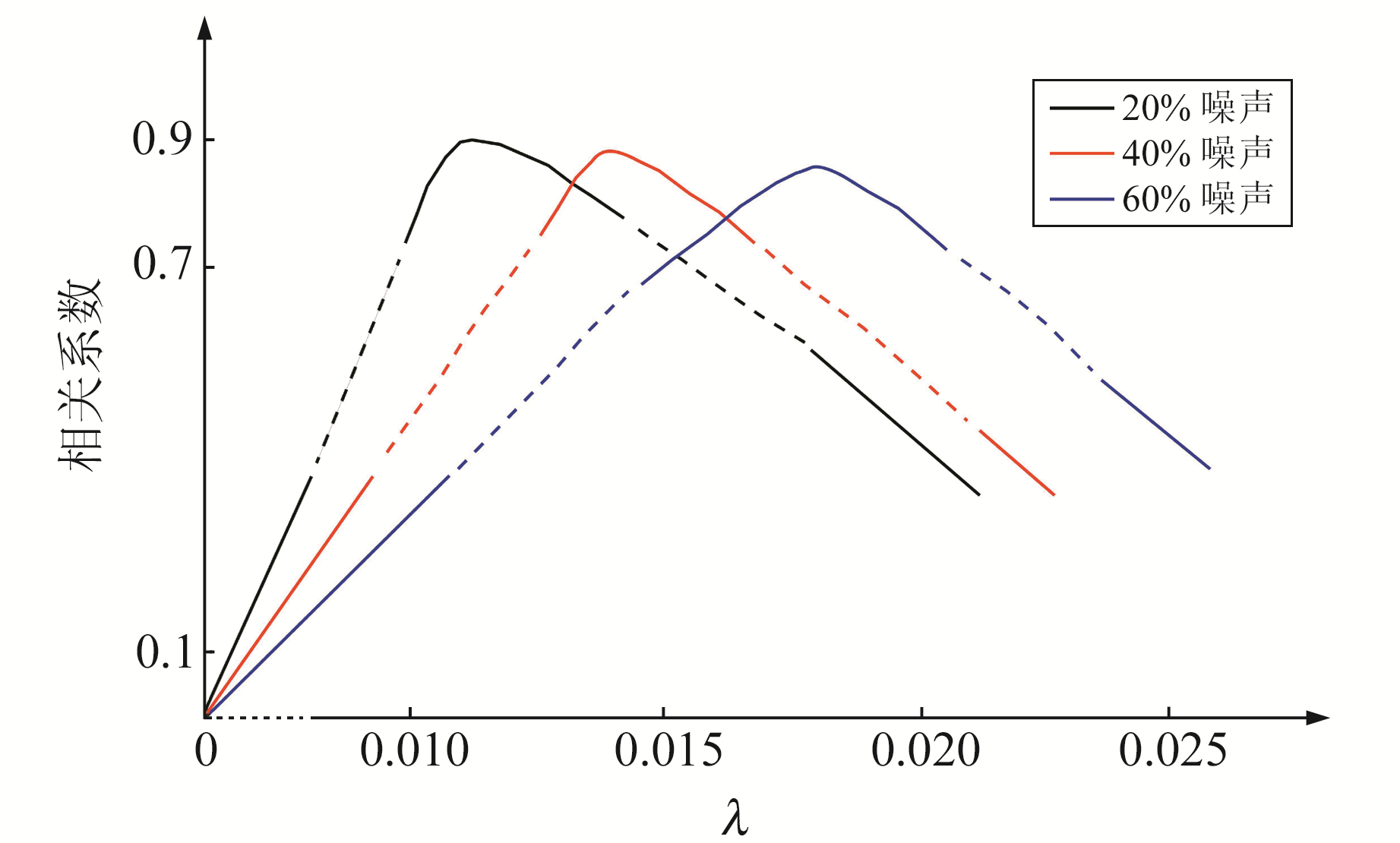
图 3为分别加入20%、40%、60%噪声的反演结果和原始序列相关性随λ变化的关系图。可以看出,当含20%随机噪声时,λ值在0.012左右时反演输出结果与原始序列的相关度达到最佳;当含40%噪声时,λ值在0.015左右时相关度比较好;当含60%噪声时,λ值在0.018左右时互相关系数达到最佳。
|
图 3 加入不同比例噪声反演结果和原始记录的相关性随λ变化关系 Fig. 3 The relationship between the correlation of different scale noise inversion results and original records with λ |
可以发现,随着噪声比例的增加,λ的最佳选取值也逐渐变大,互相关系数减小。因此在实际应用中,需根据具体数据选取合理的λ值。
2.2 L1范数楔形模型反演测试将L1范数理论应用在AVO反演中,解决薄互层反演精度不高的关键是薄互层可以表示为稀疏脉冲的组合。首先利用典型的奇偶楔形体模型分析L1范数反演方法对于薄层反演的准确性和可行性。对于薄互层,其调谐厚度tR一般使用式(12)进行计算[6]:
| $ {{{t}}_{{R}}}=\frac{\sqrt{6}}{2\text{ }\!\!\mathsf{π}\!\!\text{ }{{{f}}_{0}}} $ | (12) |
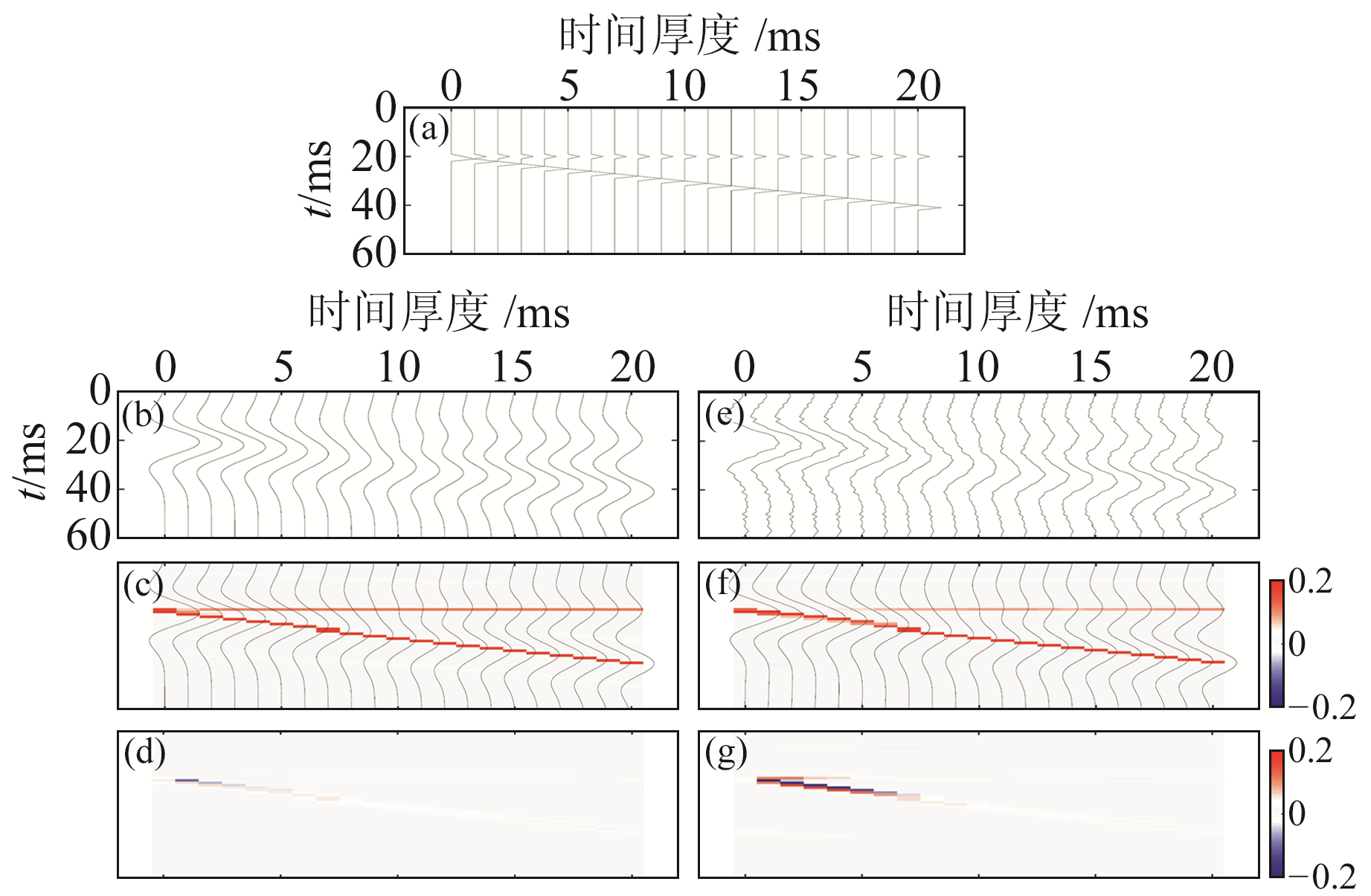
式中,f0为子波频率,测试中使用30 Hz的雷克子波,tR=10 ms。图 4为偶反射序列模型的反演结果,其中,图 4(a)为根据薄互层地震响应叠加曲线建立的偶反射序列模型,是由一系列相位相同、极性相同的脉冲对组成,水平层的反射系数为0.1,倾斜层的反射系数为0.2;图 4(b)为偶反射序列模型与子波褶积得到的合成记录;图 4(c)为反演得到的反射系数;图 4(d)为反演结果与真实反射序列图 4(a)的残差。可以看到,对于薄层反演,残差很小、分辨率较好。为了测试其抗噪性,图 4(e)为加入10%随机噪声的记录;图 4(f)为含噪数据反演结果;图 4(g)为含噪反演结果与真实反射序列图 4(a)的残差。可以看到,其具有良好的抗噪性,反演结果和理论值吻合度也比较好,但是对于0~5 ms厚度,反演结果会变差,原因是反射层距离越近,其耦合效应越严重,加入噪声后,更加影响反演结果,故得到的结果越差。
|
图 4 偶序列楔形体模型反演结果 Fig. 4 Inversion results of even-sequence wedge model |
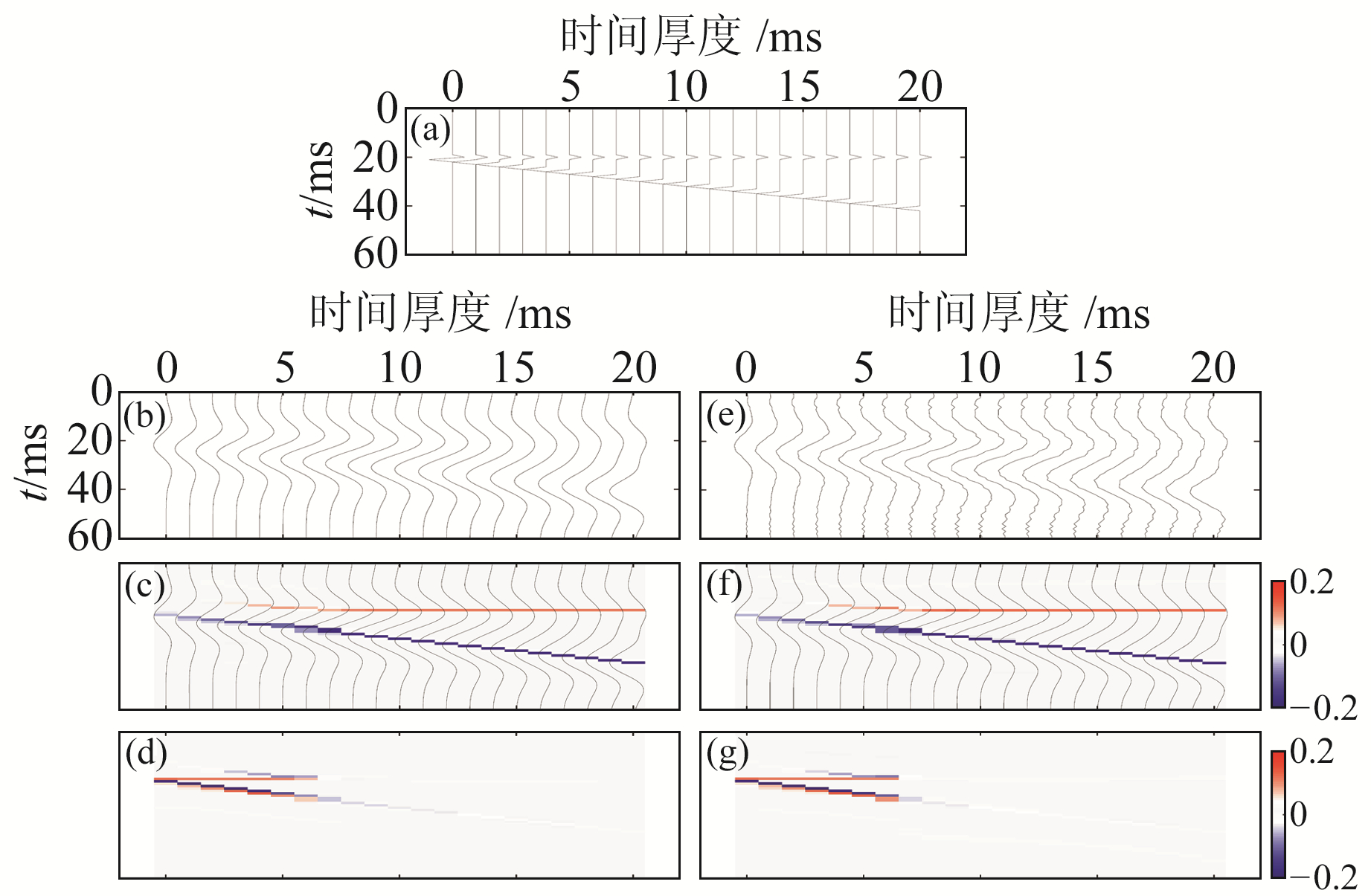
图 5为奇反射序列模型的反演结果。其中,图 5(a)为根据薄互层地震响应叠加曲线建立的奇反射序列模型,其是由一系列相位相反、极性相反的脉冲对组成,水平层的反射系数为0.1,倾斜层的反射系数为-0.2;图 5(b)为奇反射序列模型与30 Hz子波褶积得到的合成记录;图 5(c)为反演得到的反射系数;图 5(d)为反演结果与真实反射序列图 5(a)的残差。可以看到,对于薄层反演,残差很小、分辨率较好。同样,为了测试其抗噪性,图 5(e)为加入10%随机噪声的记录;图 5(f)为含噪数据反演结果;图 5(g)为含噪反演结果与真实反射序列图 5(a)的残差。可以看到,其具有良好的抗噪性,反演结果和理论值吻合度也较好。
|
图 5 奇序列楔形体模型反演结果 Fig. 5 Inversion results of the odd-sequence wedge model |
上述一系列测试表明,如果想得到满意的反演结果,需要选取合适的正则化参数。在实际数据的反演过程中,首先可以通过对井旁小部分数据进行反演,通过与测井数据对比选择合适的正则化参数,然后将其拓展到井周围,如果有多口井,即可拓展到整个工区。通过对含有薄层的楔形体模型反演测试可以看到,该算法在分辨率和抗噪方面都有很好的效果。下文将通过实际测井数据进一步对基于L1、L2范数约束反演进行对比,探究该算法在实际应用中的可行性。
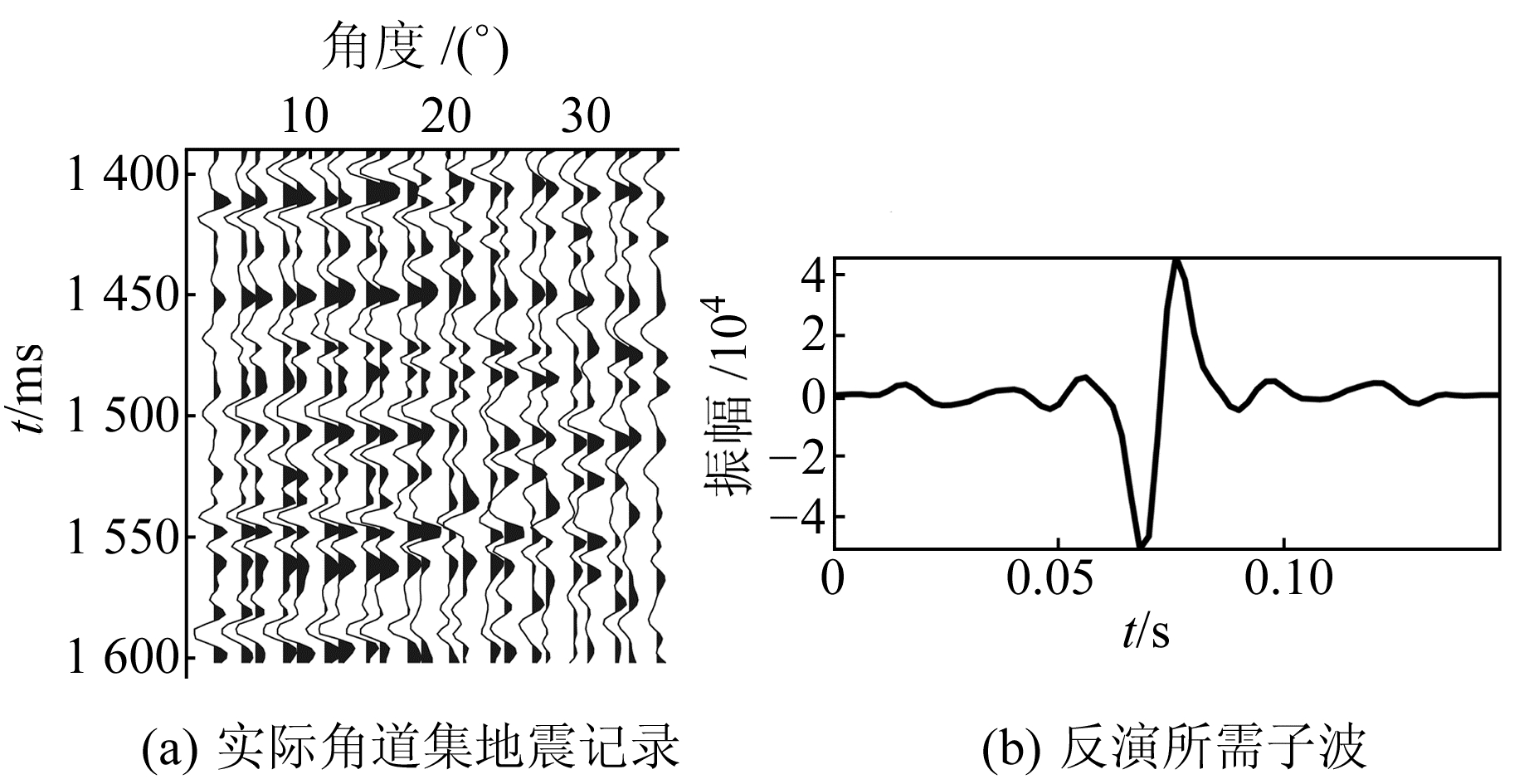
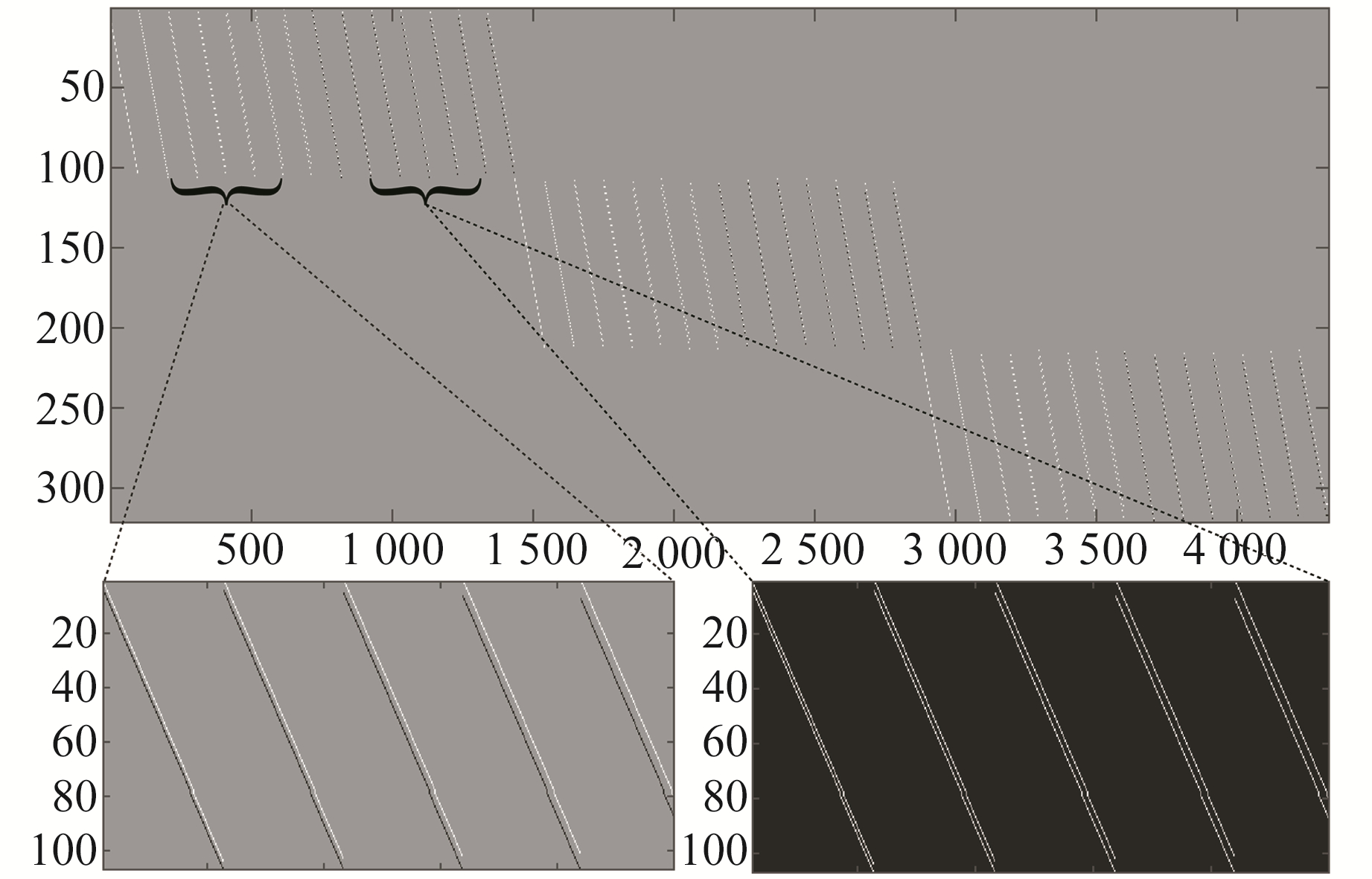
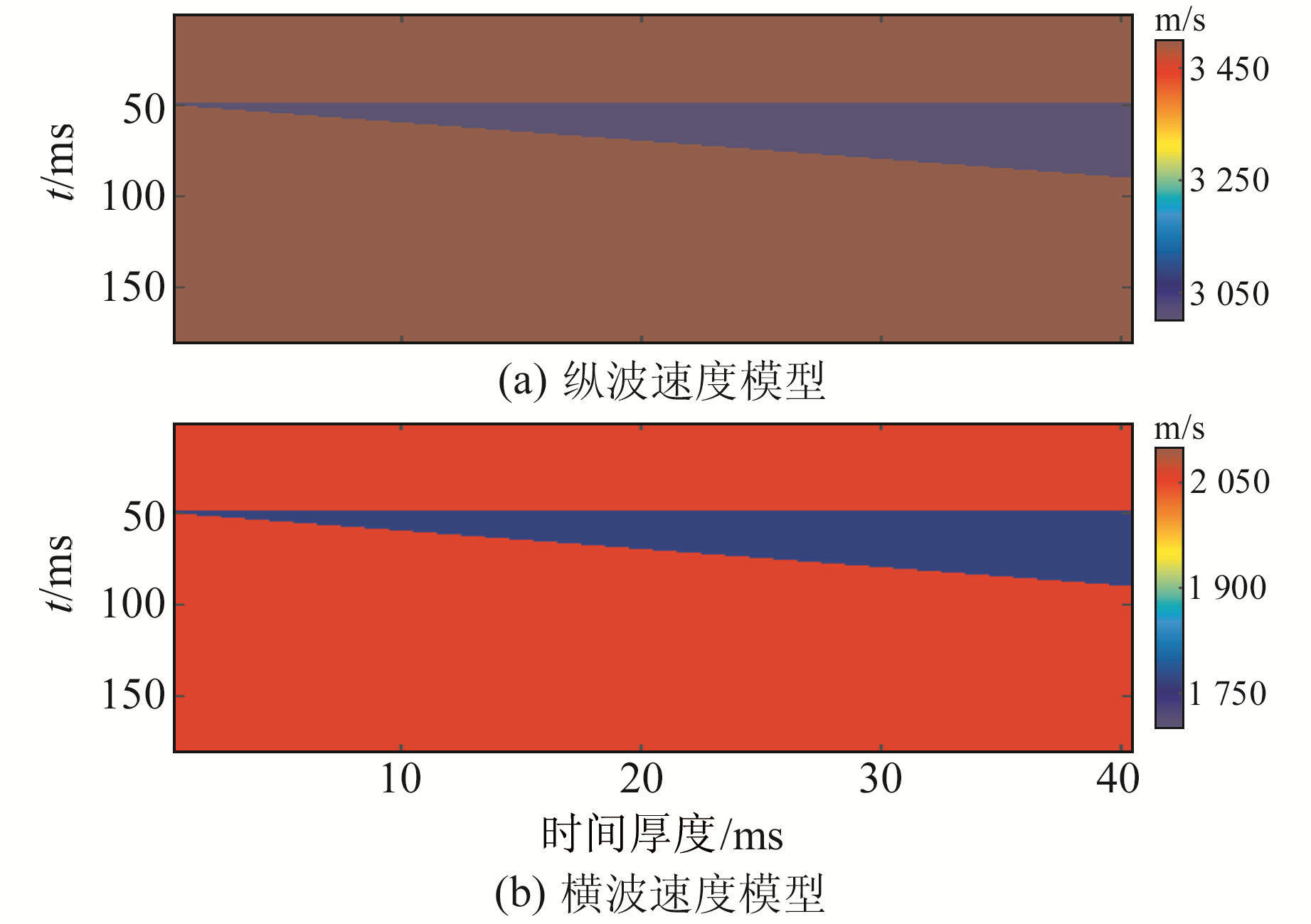
3 实际应用使用某工区的实测地震数据,该工区薄互层发育,油气指示良好。图 6(a)为实际角道集地震数据;图 6(b)为根据测井资料提取的反演所需的子波。图 7为利用实际数据创建的不同厚度的一系列楔形体字典矩阵模型(下方左侧为奇分解模型放大图,下方右侧为偶分解模型放大图)。图 8为基于实际数据得到的地下地质楔形体纵横波速度楔形体模型,其中,图 8(a)为纵波速度模型;图 8(b)为横波速度模型。
|
图 6 实际角道集地震记录和根据测井提取的反演所需子波 Fig. 6 Actual corner gather seismic records and wavelets required for inversion based on logging |
|
图 7 楔形体字典矩阵模型 Fig. 7 Wedge-shaped dictionary matrix model |
|
图 8 基于实际数据得到的地下纵横波楔形体模型 Fig. 8 Underground P-wave and S-wave wedge model based on actual data |
图 9为利用常规叠前AVO反演方法(L2范数)和L1范数反演方法得到的反演结果,图 9(a)为反演得到的角道集合成记录;图 9(b)为基于L2范数和L1范数的纵波反演结果;图 9(c)为横波反演结果,其中黑色曲线为真实测井曲线,蓝色曲线为L2范数反演结果,红色曲线为L1范数反演结果。可以看到,基于L2范数的反演结果相对光滑,基于L1范数的反演结果相对稀疏。对于纵波速度的反演结果,在图 9(b)绿色虚线框标识的位置可明显看出,通过L1范数方法得到的反演曲线与原始测试曲线吻合效果更好,L2范数的反演结果与测井曲线相反,得到了错误的反演结果。图 9(c)中横波反演结果与纵波反演结果很相似,同样在绿色虚线框区域,也显示出比较好的匹配度。

|
图 9 实际数据纵横波反演结果 Fig. 9 P-wave and S-wave inversion results of actual data |
本文在压缩感知稀疏信号采样与重建的理论基础上,将地下介质假设为块状分布,基于稀疏性假设,在L1范数约束下进行AVO反演得到纵横波反射系数,通过初始模型得到地下纵横波速度。通过模型实验证明了基于L1范数约束下AVO反演的准确性和可行性。通过实际资料反演,与传统的基于L2范数的AVO反演结果的对比显示,本文提出的基于压缩感知原理的L1范数AVO算法更加准确、分辨率更高,尤其是对于薄层的反演效果明显更好,并且在加入噪声后,算法的抗噪性也比较好。整体来说,基于L1范数约束的AVO反演运用到岩石属性预测中具有较大的潜力。但是目前缺乏一套评价结果质量的定量化标准,在有测井的区域可依据测井数据验证反演结果的优劣,对于缺乏测井数据的区域,暂时只能通过测井之间的约束进行判断,这将是后续研究的重点。
| [1] |
徐萍, 李景叶, 黄饶. 薄互层油气藏AVO特征模拟分析[J]. 中国海上油气, 2010, 22(2): 91-94 (Xu Ping, Li Jingye, Huang Rao. A Simulation Analysis of AVO Patterns in Thin-Interbedded Reservoirs[J]. China Offshore Oil and Gas, 2010, 22(2): 91-94 DOI:10.3969/j.issn.1673-1506.2010.02.004)
(  0) 0) |
| [2] |
Zhang R, Sen M K, Srinivasan S. A Prestack Basis Pursuit Seismic Inversion[J]. Geophysics, 2013, 78(1): 1-11
(  0) 0) |
| [3] |
Lin T T Y, Herrmann F J. Robust Estimation of Primaries by Sparse Inversion via One-Norm Minimization[J]. Geophysics, 2013, 78(1): 133-150
(  0) 0) |
| [4] |
Chai X T, Wang S X, Yuan S Y, et al. Sparse Reflectivity Inversion for Nonstationary Seismic Data[J]. Geophysics, 2014, 79(3): 93-105 DOI:10.1190/geo2013-0313.1
(  0) 0) |
| [5] |
Li Y D, Wang J, Yang H, et al. Fracture Characterization Using Azimuthal AVO, Ant-Tracking and Curvature[C]. SEG Annual Meeting, Houston, 2013 https://www.researchgate.net/publication/269043716_Fracture_characterization_using_azimuthal_AVO_ant-tracking_and_curvature
(  0) 0) |
| [6] |
Candes E J, Tao T. Decoding by Linear Programming[J]. IEEE Transactions on Information Theory, 2006, 51(12): 4 203-4 215
(  0) 0) |
| [7] |
焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1 651-1 622 (Jiao Licheng, Yang Shuyuan, Liu Fang, et al. Development and Prospect of Compressive Sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1 651-1 622)
(  0) 0) |
| [8] |
曹春红.压缩感知信号重建的相关理论及应用研究[D].湘潭: 湘潭大学, 2017 (Cao Chunhong. Research on the Theory and Application of Compressed Sensing Signal Reconstruction[D].Xiangtan: Xiangtan University, 2017) http://cdmd.cnki.com.cn/Article/CDMD-10530-1017257203.htm
(  0) 0) |
| [9] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分辨率[J]. 石油地球物理勘探, 2017, 52(2): 214-219 (Song Weiqi, Wu Caiduan. Seismic Data Resolution Improvement Based on Compressed Sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219)
(  0) 0) |
| [10] |
Zhang R, Castagna J. Seismic Sparse-Layer Reflectivity Inversion Using Basis Pursuit Decomposition[J]. Geophysics, 2011, 76(6): 147-158 DOI:10.1190/geo2011-0103.1
(  0) 0) |
| [11] |
Zhang R, Sen M K, Phan S, et al. Stochastic and Deterministic Seismic Inversion Methods for Thin-Bed Resolution[J]. Journal of Geophysics and Engineering, 2012, 9(5): 611-618 DOI:10.1088/1742-2132/9/5/611
(  0) 0) |
2. Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071, China
 2020, Vol. 40
2020, Vol. 40


