2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 西部矿产资源与地质工程教育部重点实验室,西安市雁塔路126号,710054
滑坡监测是准确预报滑坡的重要技术手段。目前已有多种滑坡监测方法,如常规大地测量方法、位移传感器以及GNSS技术等。其中,GNSS技术因具有全天候定位服务、操作简便、精度较高等优点,已成为滑坡监测中的首选技术。滑坡从出现变形到最终失稳一般经历初始变形阶段、匀速变形阶段和加速变形阶段3个过程。当滑坡变形处在初始变形阶段以及匀速变形阶段时,其变形量较小,而GNSS技术易受多路径效应的影响,导致获取的形变量并不是滑坡真实的形变量,而是真实形变量与各类噪声的混合信息,此混合信息对滑坡变形预测预报的精度与可靠性产生严重影响。因此,有必要采取适当的方法去除监测信息中的噪声,以获取滑坡监测点的真实形变量,准确提取监测点的变形特征。
从含有噪声的信号中提取监测点的变形特征,最有效的方法是对信号进行抑噪处理,以凸显其形变特征[1]。常用的抑噪方法分为2种:1)基于统计理论的抑噪方法;2)时频分析抑噪方法。相较于统计理论抑噪方法而言,时频分析抑噪方法应用更为广泛且有效[2-6]。常用的时频分析方法有短时傅里叶变换和小波变换。短时傅里叶变换由于窗函数不能改变窗口的形状,因此不适用于非平稳信号。小波分析能够对非平稳信号进行降噪,但小波阈值的选取、小波阈值函数的确定较为复杂[7]。此外,小波基函数的选取也有较大的不确定性,导致利用小波变换无法获取较为准确且可靠的形变信息。1996年Stoekwel等[8]提出一种介于短时傅里叶变换和小波变换之间的非平稳信号分析方法——S-变换(S transform,ST)。S-变换结合了短时傅里叶变换与小波变换的优点,克服了短时傅里叶变换时频窗口在时频平面中不可变的问题,已广泛应用在地震领域[9-13],但在滑坡变形监测领域少有涉及。本文探讨将S-变换方法引入滑坡变形监测数据处理分析中的可行性,并通过设计时频滤波器,提取监测点较为准确、可靠的变形信息。
1 S-变换对于给定的时间信号h(t),其S-变换标准定义式为[14]:
| $ {S}\left( {\tau, f} \right) = \mathop \smallint _{ - \infty }^\infty h\left( t \right) \times \frac{{\left| f \right|}}{{\sqrt {2\mathsf{π} } }} \times {{\rm e}^{\frac{{{{\left( {\tau - t} \right)}^2} \times {f^2}}}{2}}} \times {{\rm e}^{ - {\rm i}2\mathsf{π} ft}}{\rm d}t $ | (1) |
式中,S=(τ,f)为信号h(t)的S-变换,t为时间,f为频率,τ为控制窗口移动的参数。
利用傅里叶反变换可以实现S-逆变换,重构时域信号:
| $ {{h}}\left( {{t}} \right) = \mathop \smallint _{ - \infty }^\infty \left( {\mathop \smallint _{ - \infty }^\infty S\left( {\tau , f} \right){\rm d}\tau } \right) \times {{\rm e}^{{\rm i}2\mathsf{π} ft}}{\rm{d}}f $ | (2) |
信号h(t)经过S-变换后得到一个二维复时频矩阵,记为S(t,f),其中行向量对应频率,列向量对应采样时刻。将S(t,f)中各元素求模后的矩阵记为S|(t,f)|,其行向量表示某一频率下信号随采样时刻变化的分布,列向量表示某一采样时刻下信号随频率变化的分布。S|(t,f)|中各元素反映了信号在其对应时刻及频率下的时频特征。
S-变换的滤波过程可以表示为:
| $ h\left( t \right) = {S^{ - 1}}\left( {S\left( {h\left( t \right)} \right) \times {H_{\rm TF}}\left( {\tau, f} \right)} \right) $ | (3) |
式中,S和S-1分别为正变换与反变换,HTF(τ,f)为时频滤波器:
| $ {H_{\rm TF}} = \left\{ {\begin{array}{*{20}{c}} {1, (\tau , f) \in D}\\ {0, (\tau, f) \notin D} \end{array}} \right\} $ | (4) |
式中,D为指定信号的时频通域,由于变形监测过程中随机噪声分布在各个时间点处,因此,D为整个时频通域。
由S-变换结果可知,时频滤波器的设计主要有2种方式:1)根据S(t,f)设计;2)根据S|(t,f)|设计。考虑到第1种方式会改变系数的相位,从而使S逆变换重构得到的时域信号产生附加噪声[1],因此本文根据最大最小值理论,按照S|(t,f)|设计滤波器。定义如下时频滤波器:
| $ {H_{\rm TF}}\left( i \right) = {\left( {\frac{{{{S}}\left| {\left( {{t_i}, f} \right)} \right| - {M_i}}}{{{\rm{max}}\left( {{{S}}\left| {\left( {{t_i}, f} \right)} \right| - {M_i}} \right)}}} \right)^{\frac{1}{3}}} $ | (5) |
式中,Mi为ti时刻振幅谱中S|(ti,f)|的最小值。具体抑噪过程如图 1所示。
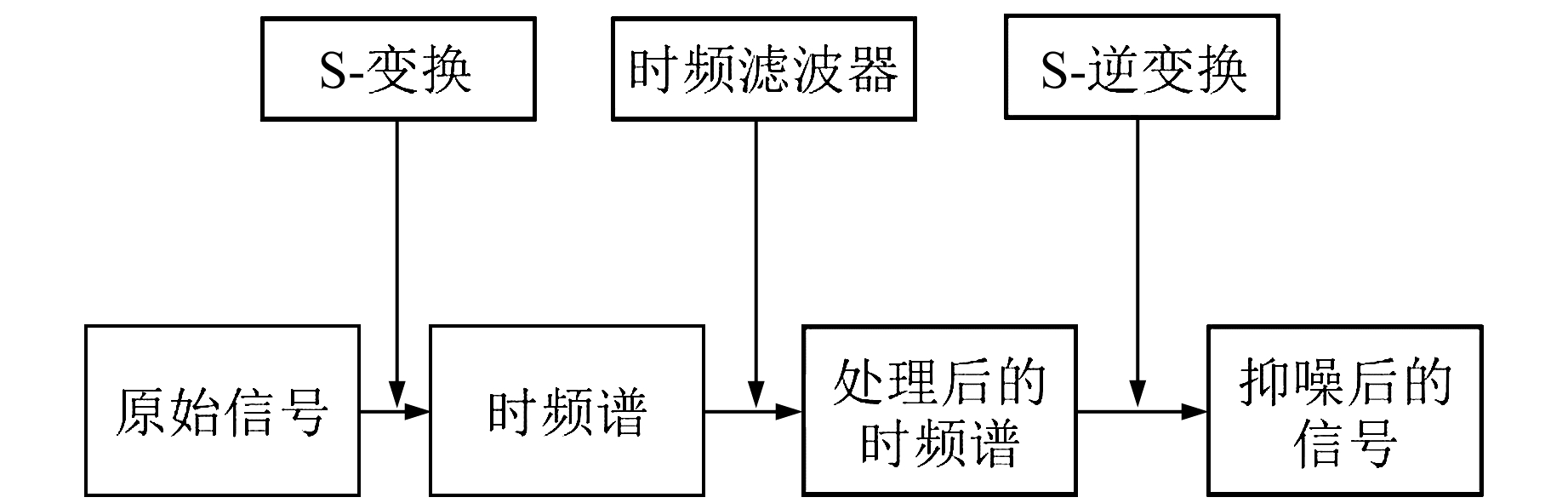
|
图 1 基于S-变换的抑噪过程 Fig. 1 S-transformation based on denoising process |
为了验证所提方法的性能,采用如下模拟信号进行分析。模拟信号主体为低频信号,在不同的时间段添加不同频率的信号,以验证S-变换具有多分辨率特性(模拟信号如图 2(a)):
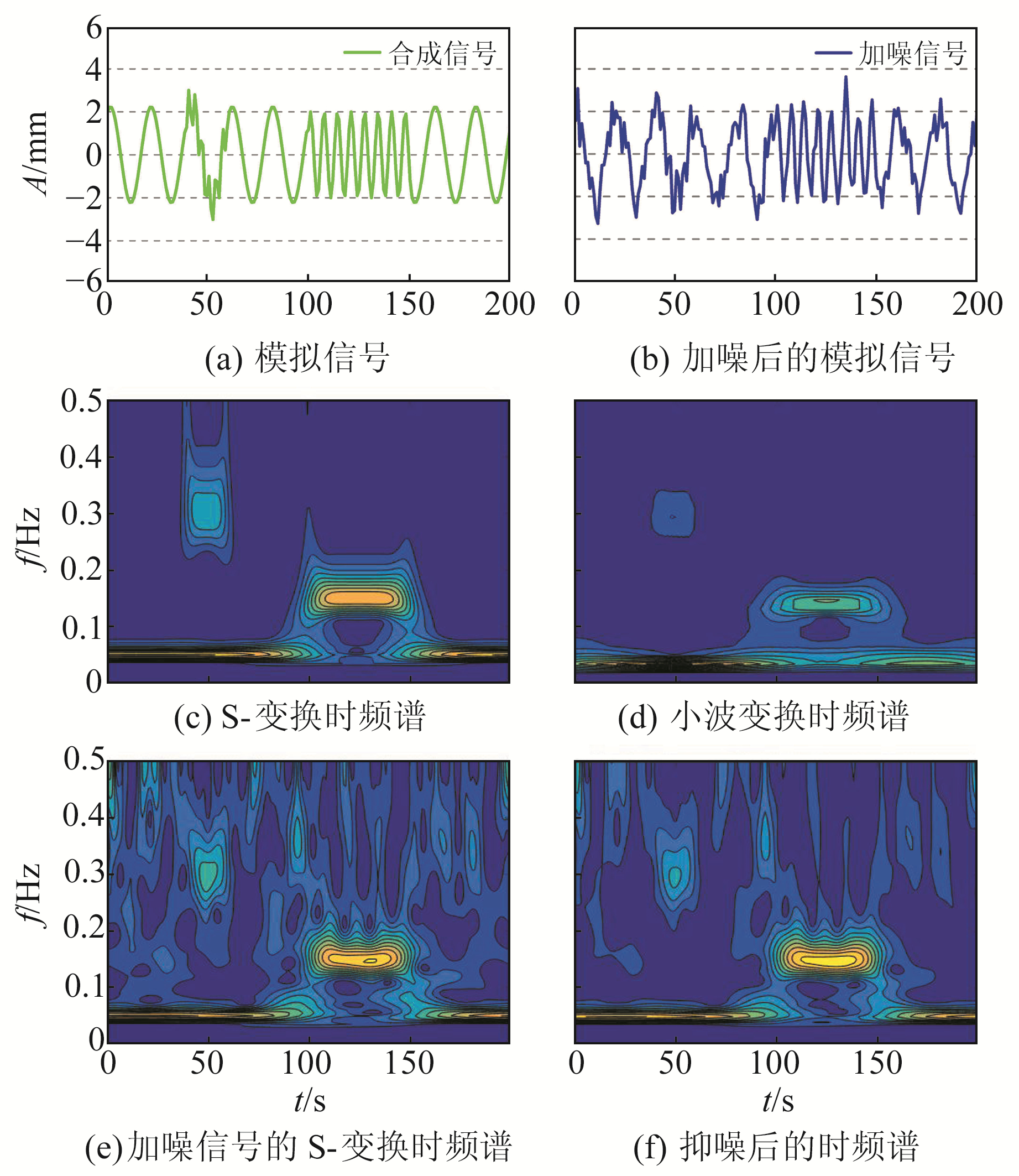
|
图 2 模拟信号及时频分析 Fig. 2 Analog signal time and frequency analysis |
| $ \left\{ {\begin{array}{*{20}{l}} {h\left( t \right) = 2 \times \cos \left( {2\mathsf{π} \times {\rm lowfred} \times t} \right) + 2 \times \sin \left( {2\mathsf{π} \times {\rm lowfred} \times t} \right)}\\ {h\left( {40:60} \right) = h\left( {40:60} \right) + \cos \left( {2\mathsf{π} \times {\rm highfred} \times t} \right)}\\ {h\left( {100:150} \right) = 2 \times \cos \left( {2\mathsf{π} \times {\rm midfred} \times t} \right)} \end{array}} \right. $ | (6) |
式中,lowfred=10 Hz,midfred=30 Hz,highfred=60 Hz,信号长度为200。在模拟信号中加入信噪比为5的随机噪声,如图 2(b)所示,图 2(e)为加噪信号经过S-变换后的时频谱,图 2(f)为加噪信号经过S-变换滤波后的时频谱。
对模拟信号进行S-变换,得到S-变换时频谱(图 2(c))。可以看出,S-变换能够准确地从模拟信号中提取信号的变换特征。图 2(d)为模拟信号的小波变换时频谱,虽然小波变换也能提取出模拟信号的特征,但从结果来看,只得到了信号变化的位置,并不能详细反映信号的变化特征。本文利用基于S-变换的抑噪方法对模拟信号进行处理,从时频谱中可以看出,滤波后的时频谱较为“干净”。sym6小波滤波方法的评价指标优于其他小波以及中值滤波方法[4],因此,对模拟信号采用sym6小波滤波方法进行处理,并对二者的结果进行对比分析(图 3)。
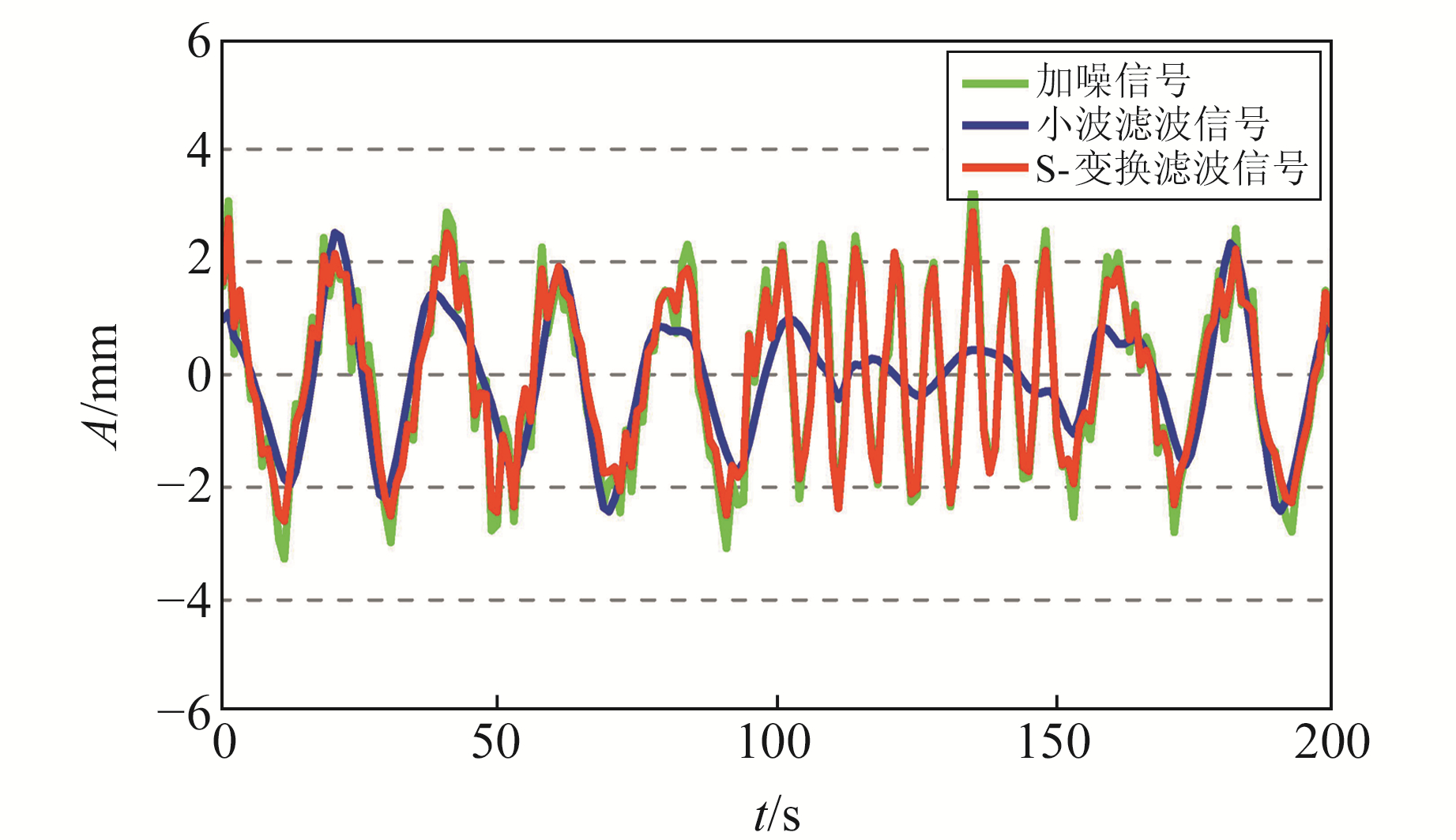
|
图 3 原始信号与滤波信号 Fig. 3 Original signal and filtered signal |
从图 3可以看到,小波抑噪方法尽管有效地降低了噪声的影响,但同时也湮没了一部分信号的变化特征,尤其在中、高频部分较为明显;而经过S-变换滤波后的信号在降低噪声的同时,也很好地反映了模拟信号的波动趋势。
使用均方根误差(RMSE)和信噪比(SNR)参数分析信号经不同方法降噪后的性能差异:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_n {{\left( {y - \hat y} \right)}^2}} $ | (7) |
| $ {\rm{SNR}} = 10 \times {\rm{l}}{{\rm{g}}}\left( {P/{\rm RMSE}{^2}} \right) $ | (8) |
式中,y为原始信号,
从图 4及表 1可以发现,经过S-变换滤波后的RMSE为0.262 1,SNR为15.493 4;而经过小波滤波后的RMSE为1.089 3,SNR为3.121 6。分析可得,本文提出的S-变换滤波方法的RMSE和SNR均明显优于目前常用的小波滤波方法,且利用S-变换滤波方法能够较为准确地反映仿真信号的变化特征。

|
图 4 经S-变换与小波变换滤波信号的RMSE序列 Fig. 4 RMSE sequence of filtered signals by S-transform and wavelet transform |
|
|
表 1 2种滤波方法滤波评价指标比较 Tab. 1 Comparison of two filtering methods for filtering evaluation indicators |
本文所采用的观测数据来自陕西省泾阳县太平镇庙店村,该村位于泾河南岸,是黄土滑坡频发地带。滑坡体平面形态呈上陡-下缓的形态(图 5(a))。滑坡监测网(图 5(b))中使用北斗/GNSS接收机进行实时观测,并采用长安大学北斗分析中心自主研发的北斗/GNSS实时监测系统获得的监测点N、E、U方向点坐标变化序列的小时解,数据采集时间为2018-08-28 17:00~2019-04-17 02:00,共1 913个历元,基准站设在距离滑坡体约400 m处的稳定地带。选取MD09监测点坐标变化序列进行分析,结果如图 6所示。
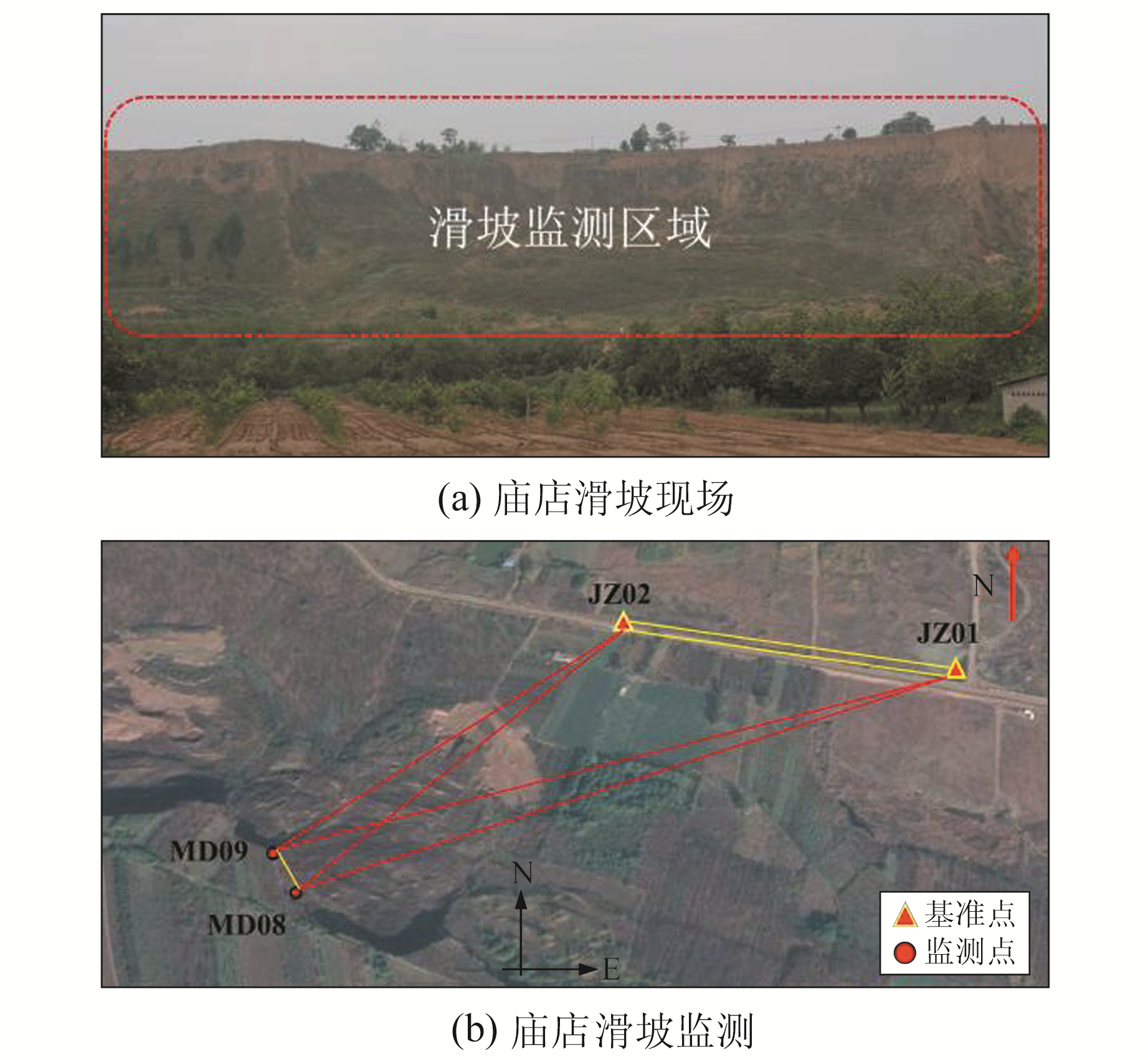
|
图 5 庙店滑坡现场及监测网 Fig. 5 Miaodian landslide site and monitoring network |
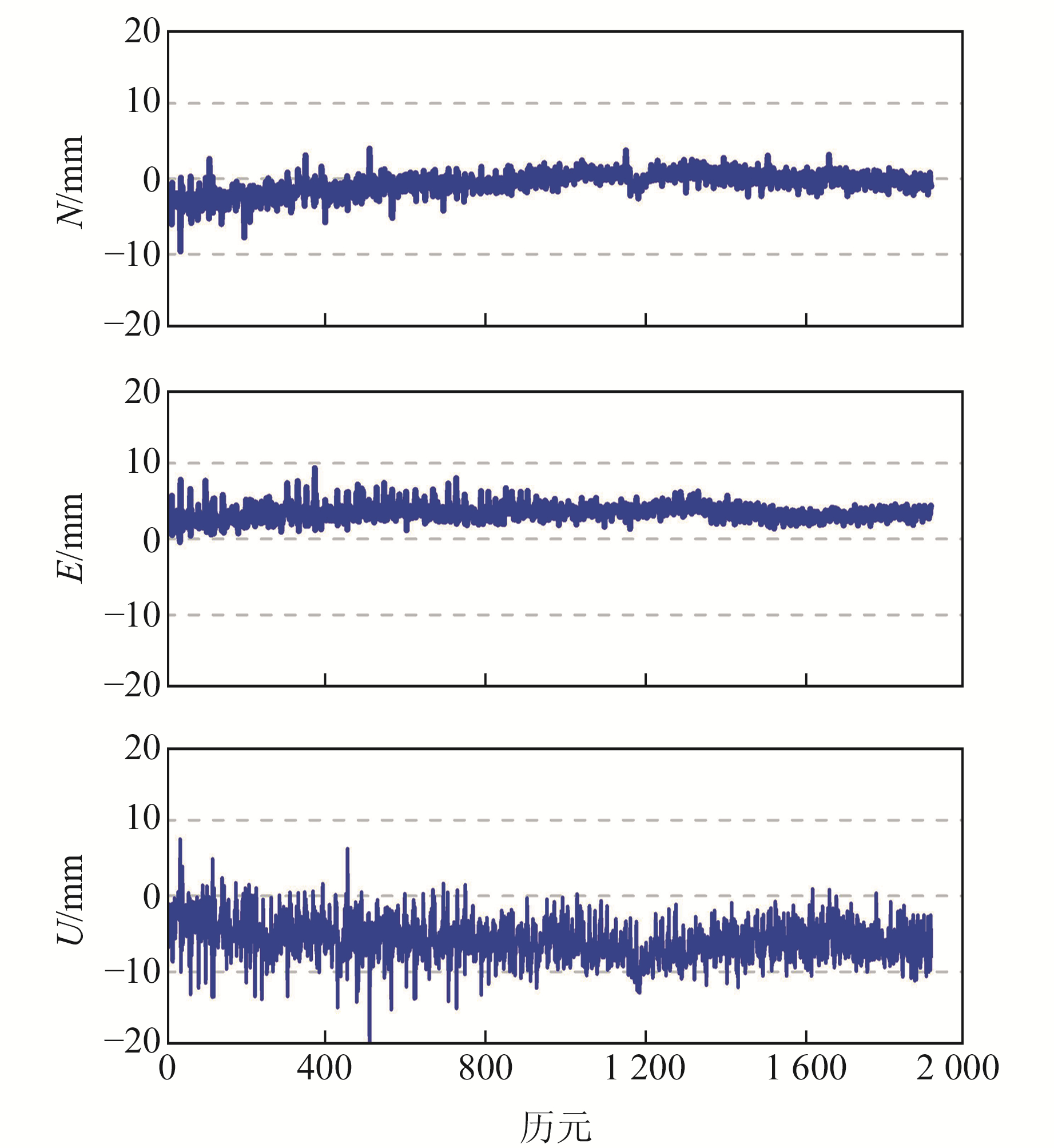
|
图 6 N、E、U方向形变数据序列 Fig. 6 Deformation data sequence in N, E, U directions |
从图 6可以看出,监测点的形变序列中包含有明显的噪声,该数据不能直接用于后续的变形预报阶段。因此,需要对数据进行抑噪处理,准确获取监测点的真实形变量,提取监测点的变形特征。从图 7可以发现,利用S-变换方法与小波分析方法均可降低噪声对信号的影响,但利用小波滤波方法降低噪声的同时也湮没了部分有效信息。相比于小波滤波方法,利用S-变换滤波方法可以较好地保留信号的有效信息,识别出监测点真实的变形信息。

|
图 7 原始信号与经过不同滤波方法的信号 Fig. 7 Original signal and signal with different filtering methods |
从图 8及表 2可以看出,N、E、U方向S-变换滤波方法均优于小波滤波方法,因此可以得出,经过S-变换的滤波方法可以有效降低信号的均方根误差、提高信噪比,且能较准确地提取监测点的真实形变量,反映监测点的形变特征。

|
图 8 经S-变换与小波变换滤波信号的RMSE序列 Fig. 8 RMSE sequence of filtered signals by S-transform and wavelet transform |
|
|
表 2 2种滤波方法滤波评价指标比较 Tab. 2 Comparison of two filtering methods for filtering evaluation indicators |
本文探讨了将S-变换方法引入滑坡变形监测数据处理分析中的可行性,由仿真数据及实际变形监测数据的分析,可以得到以下结论:
1) 在模拟实验中,通过对比采用不同滤波方法滤波后模拟信号的RMSE和SNR可以得到,基于S-变换的滤波方法处理后的模拟信号在RMSE和SNR上均优于目前常用的小波滤波方法,且利用S-变换滤波方法能够较为准确地反映仿真信号的变化特征。所以,S-变换是一种有效的时频分析方法,能够分辨出信号任意时刻对应的频率特征,弥补了小波变换的不足。
2) 将S-变换滤波方法应用于泾阳县庙店村滑坡变形监测数据处理中,通过对N、E、U方向的计算分析可得,基于S-变换滤波方法处理后的变形数据在RMSE和SNR上均优于目前常用的小波滤波方法。基于S-变换的滤波方法有效降低了信号均方根误差,提高了信噪比,较准确地提取了监测点的真实形变量,反映了监测点的形变特征,能够为滑坡变形预测预报提供可靠的数据,提高滑坡变形预测预报的精度。
| [1] |
郭远晶, 魏燕定, 周晓军. 基于S变换谱阈值去噪的冲击特征提取方法[J]. 振动与冲击, 2014, 33(21): 44-50 (Guo Yuanjing, Wei Yanding, Zhou Xiaojun. An Impact Feature Extracting Method Based on S-Transformation Spectrum Threshold Denoising[J]. Journal of Vibration and Shock, 2014, 33(21): 44-50)
(  0) 0) |
| [2] |
李旋, 戴吾蛟, 陈永奇, 等. 基于小波变换的GPS动态变形分析[J]. 测绘科学, 2008, 33(6): 55-56 (Li Xuan, Dai Wujiao, Chen Yongqi, et al. GPS Dynamic Deformation Analyse Based on Wavelet Transform[J]. Science of Surveying and Mapping, 2008, 33(6): 55-56 DOI:10.3771/j.issn.1009-2307.2008.06.018)
(  0) 0) |
| [3] |
李潇, 徐进军. 基于小波分析与LSSVM的滑坡变形预测[J]. 大地测量与地球动力学, 2009, 29(4): 127-130 (Li Xiao, Xu Jinjun. Landslide Deformation Prediction Based on Wavelet Analysis and Least Square Support Vector Machine[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 127-130)
(  0) 0) |
| [4] |
黄连英. 基于小波分析的GPS动态监测数据变形特征分析方法[J]. 长春工程学院学报:自然科学版, 2012, 13(3): 15-20 (Huang Lianying. The Analysis of Deformation Characteristics to GPS Dynamic Monitoring Data Based on Wavelet Analysis[J]. Journal of Changchun Institute of Technology:Natural Science Edition, 2012, 13(3): 15-20)
(  0) 0) |
| [5] |
张凯翔, 牛瑞卿, 胡友健, 等. 基于小波变换及外因响应的滑坡位移预测[J]. 中国矿业大学学报, 2017(4): 924-931 (Zhang Kaixiang, Niu Ruiqing, Hu Youjian, et al. Landslide Displacement Prediction Based on Wavelet Transform and External Cause[J]. Journal of China University of Mining & Technology, 2017(4): 924-931)
(  0) 0) |
| [6] |
王涛, 田林亚, 孔令杰, 等. GPS高层建筑物动态特性的小波分析提取[J]. 测绘科学, 2018, 43(4): 100-104 (Wang Tao, Tian Linya, Kong Lingjie, et al. Wavelet Analysis Extraction Using GPS High-Rise Buildings Dynamic Feature[J]. Science of Surveying and Mapping, 2018, 43(4): 100-104)
(  0) 0) |
| [7] |
王振生, 王峰林, 王长龙. 基于S变换的复合材料超声回波信号降噪[J]. 仪表技术与传感器, 2014(3): 104-106 (Wang Zhensheng, Wang Fenglin, Wang Changlong. De-Noising of S-Transform on Ultrasonic Echo Signal of Metal Matrix Composites[J]. Instrument Technique and Sensor, 2014(3): 104-106 DOI:10.3969/j.issn.1002-1841.2014.03.034)
(  0) 0) |
| [8] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the Complex Spectrum: The S Transform[J]. IEEE Transactions on Signal Processing, 1996, 44: 998-1 001 DOI:10.1109/78.492555
(  0) 0) |
| [9] |
陈学华, 贺振华, 黄德济. 基于广义S变换的信号提取与抑噪[J]. 成都理工大学学报:自然科学版, 2006, 33(4): 331-335 (Chen Xuehua, He Zhenhua, Huang Deji. Signal Extraction and Noise Suppression Based on Generalized S Transform[J]. Journal of Chengdu University of Technology: Science and Technology Edition, 2006, 33(4): 331-335)
(  0) 0) |
| [10] |
赵淑红, 朱光明. S变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4): 402-406 (Zhao Shuhong, Zhu Guangming. S Transform Time-Frequency Filtering Denoising Method[J]. Oil Geophysical Prospecting, 2007, 42(4): 402-406 DOI:10.3321/j.issn:1000-7210.2007.04.008)
(  0) 0) |
| [11] |
樊剑, 涂家祥, 吕超, 等. 采用时频滤波技术的近断层脉冲地震人工模拟[J]. 华中科技大学学报:自然科学版, 2008, 36(11): 116-119 (Fan Jian, Tu Jiaxiang, Lü Chao, et al. Generation of Artificial Near-Fault Ground Motions Based on Time-Frequency Filtering[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2008, 36(11): 116-119)
(  0) 0) |
| [12] |
王云专, 兰金涛, 龙玉沙. 基于S变换的随机噪声压制方法[J]. 地球物理学进展, 2010, 25(2): 562-567 (Wang Yunzhuan, Lan Jintao, Long Yusha. The Method for Attenuating Random Noise Based on S Transform[J]. Progress in Geophysics, 2010, 25(2): 562-567 DOI:10.3969/j.issn.1004-2903.2010.02.026)
(  0) 0) |
| [13] |
张小红, 郭斐, 郭博峰, 等. 利用高频GPS进行地表同震位移监测及震相识别[J]. 地球物理学报, 2012, 55(6): 1 912-1 918 (Zhang Xiaohong, Guo Fei, Guo Bofeng, et al. Coseismic Displacement Monitoring and Wave Picking with High-Frequency GPS[J]. Chinese Journal of Geophysics, 2012, 55(6): 1 912-1 918)
(  0) 0) |
| [14] |
Ranjan R, Singh A K, Jindal N. Formulation of Some Useful Theorems for S-Transform[J]. Optik, 2018, 168: 913-919 DOI:10.1016/j.ijleo.2018.05.009
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education, 126 Yanta Road, Xi'an 710054, China
 2020, Vol. 40
2020, Vol. 40


