2. 中国科学院大学,北京市玉泉路19号甲,100049
地球重力场观测数据是地理空间信息的重要组成部分,获取重力场观测数据的手段分为地面重力测量、卫星重力测量和海洋航空(简称海空)重力测量,其中海空重力测量能够填补卫星重力测量和地面重力测量之间的重力频谱范围,是一种高效的测量手段[1-4]。
格值是海空重力仪中一个重要的标定参数,是指将重力仪的计数单位(俗称“格”)转换为重力单位mGal的标定函数,也称格值函数[2, 5]。对于高精度的地面静态重力仪,主要采用长基线法、短基线法和垂直基线法,为减小误差,一般在测程范围内分段标定重力仪[6-7]。海洋重力仪的格值标定可参考陆地静态重力仪的标定[5, 8-9]。
20世纪80年代末,中科院测量与地球物理研究所成功研制CHZ海洋重力仪,并进行了3次海洋重力测量实验,包括与KSS-30海洋重力仪同船比对测试。结果表明,CHZ海洋重力仪在恶劣海况下依然能稳定工作,性能略优于KSS-30海洋重力仪,交叉点精度为1 mGal[10-12]。20世纪90年代初,CHZ海洋重力仪先后2次在国产Z-8直升机上进行了我国早期的航空重力测量实验,结果表明,其动态性能符合航空重力测量需求[13]。进入21世纪,在科技部重大仪器专项的支持下,中科院测量与地球物理研究所在原有的CHZ海洋重力仪基础上开始研制新一代的CHZ-Ⅱ海空重力仪。由于格值准确性在重力测量成果中的重要作用,本文首先介绍了倾斜法标定格值,然后将其应用于国产自主研发的CHZ-Ⅱ海空重力仪格值标定,得到实验室标定的格值结果。
1 倾斜法标定格值重力仪输出的是电压值,而我们需要得到的是以重力单位表示的重力值,但这两者之间没有必然联系,因此必须预先获得重力仪的标定函数,以便将重力仪的读数转换成重力值[2, 14]。要精确得到标定函数就必须精确知道重力仪本身的物理参数和其他的一些参数,各种参数之间的关系错综复杂,由各种参数通过理论计算得到精确的标定函数是非常难做到的。因此,一般由模型来模拟标定函数,模型中各个参数是与已知重力值比较后推算出来的。
如果将重力值随时间变化的因素忽略不计,则标定函数可用式(1)表示:
| $g=F(Z) $ | (1) |
式中,g为重力值,Z为重力仪读数。
倾斜法是一种在实验室内标定格值的方法, 该方法简单、易行,可以避免基点联测中由仪器搬运产生的不利因素[8]。倾斜法原理如图 1(a)所示,当倾斜重力仪的敏感探头时,重力仪的测量轴也随之倾斜相同的角度。在实际实验中把重力仪的敏感探头固定在Hexapod六自由度平台上,如图 1(b)所示,通过控制六自由度平台倾斜一定的角度使重力仪探头也随之倾斜相同的角度。已知某个测点的重力值g0及重力仪探头测量轴在垂直方向时的电压读数为Z0,假设将平台倾斜某个角度θ,此时相对应的重力仪探头电压读数为Zθ,作用在重力仪测量轴上的重力加速度变为g0cosθ。根据式(1),假设重力变化值和重力仪电压读数成正比,重力仪格值为常数K,则有:

|
图 1 重力仪探头倾斜测量 Fig. 1 Gravimeter tilt |
| $\delta g=g_{0}-g_{0} \cos \theta=K\left(Z_{0}-Z_{\theta}\right) $ | (2) |
根据式(2)可得格值:
| $K=g_{0}-g_{0} \cos \theta /\left(Z_{0}-Z_{\theta}\right) $ | (3) |
已知六自由度平台倾斜角度和测点重力值可以计算出重力变化值,采集软件记录相应的重力仪探头电压读数,利用重力变化值和电压变化值拟合出一条直线,直线的斜率即为重力仪的格值。另一种拟合方法也是假设重力变化值和电压变化值成正比,根据已知的重力变化和角度变化,拟合电压变化和角度变化,其原理如下。
1) 由式(2)可得:
| $K\left(Z_{0}-Z_{\theta}\right)=g_{0}-g_{0} \cos \theta=g_{0}(1-\cos \theta) $ | (4) |
2) cosθ可以采用级数展开为:
| $\begin{aligned} \cos \theta=& 1-\frac{\theta^{2}}{2 !}+\frac{\theta^{4}}{4 !}-\frac{\theta^{6}}{6 !}+\frac{\theta^{8}}{8 !}-\cdots+\\ &(-1)^{n-1} \frac{\theta^{2 n-2}}{(2 n-2) !}+\cdots \end{aligned} $ | (5) |
3) 将式(5)代入式(4)得:
| $\begin{array}{*{20}{c}} {{Z_0} - {Z_\theta } = {g_0}(1 - \cos \theta )/K = }\\ {{g_0}\left( {\frac{{{\theta ^2}}}{{2!}} - \frac{{{\theta ^4}}}{{4!}} + \frac{{{\theta ^6}}}{{6!}} - \frac{{{\theta ^8}}}{{8!}} \cdots } \right)/K \approx \frac{{{g_0}}}{{2K}}{\theta ^2}} \end{array} $ | (6) |
需要强调的是,式(6)在小角度倾斜时才可以近似。拟合电压变化和角度变化的关系得到拟合曲线二次项的系数值,根据已知的g0就可以算出重力仪的格值。
2 CHZ-Ⅱ海空重力仪格值实验CHZ-Ⅱ海空重力仪采用轴对称垂直弹簧悬挂系统,高精度电容微位移传感器,拉丝和绷簧用于限制采样质量除竖直方向外其余自由度的运动,以抑制水平交叉耦合效应[15]。
在实验室中将CHZ-Ⅱ海空重力仪的敏感探头固定在六自由度平台上,通过控制六自由度平台的倾斜角度,使重力仪的敏感探头倾斜相应的角度。六自由度平台的标称精度为0.2″,理论上可认为平台倾斜角度没有误差。实验按照10 mGal、20 mGal、50 mGal、100 mGal、200 mGal的台阶变化,每档设计10个台阶,六自由度平台从水平开始倾斜到最大角度共有50个台阶,然后回到水平,再由对称的负方向倾斜到最大角度再回到水平位置,总共有200个台阶。根据式(2)计算的变化角度见表 1,表中的重力变化和角度变化都是参考重力仪敏感探头垂直向下的状态。定义重力仪探头的2个水平正交轴分别为U轴和V轴,并依次对其进行实验,在每个变化角度上静置20 min,等待重力仪读数稳定。
|
|
表 1 重力变化对应的角度变化 Tab. 1 Angle change corresponding to gravity change |
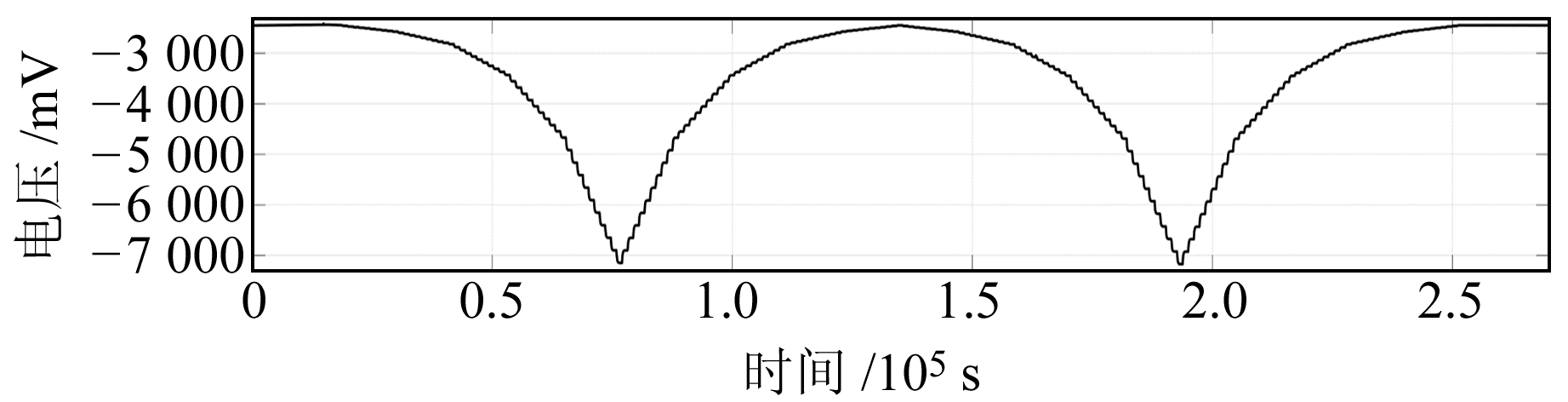
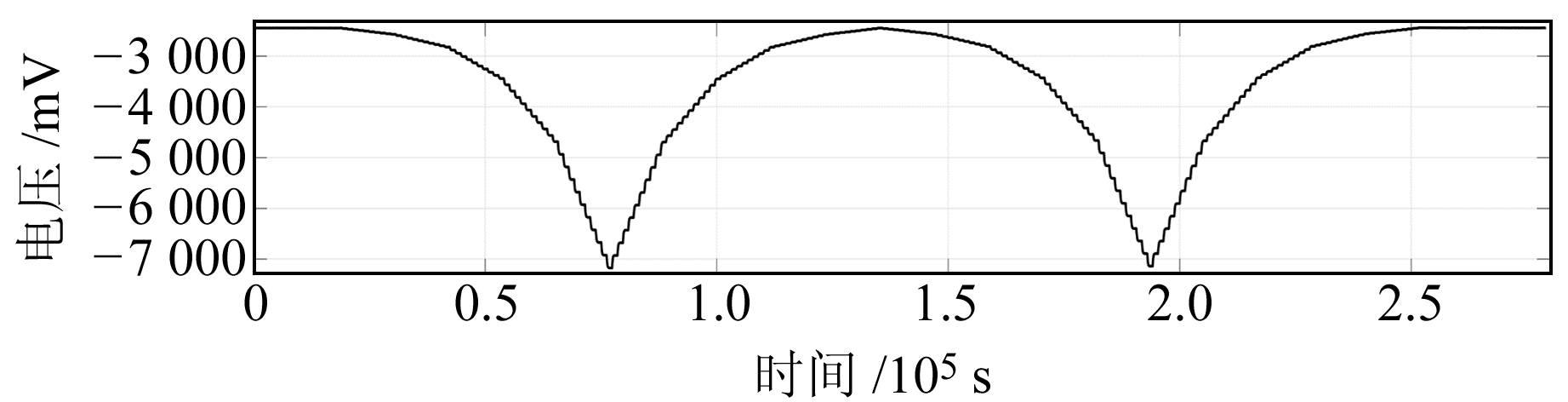
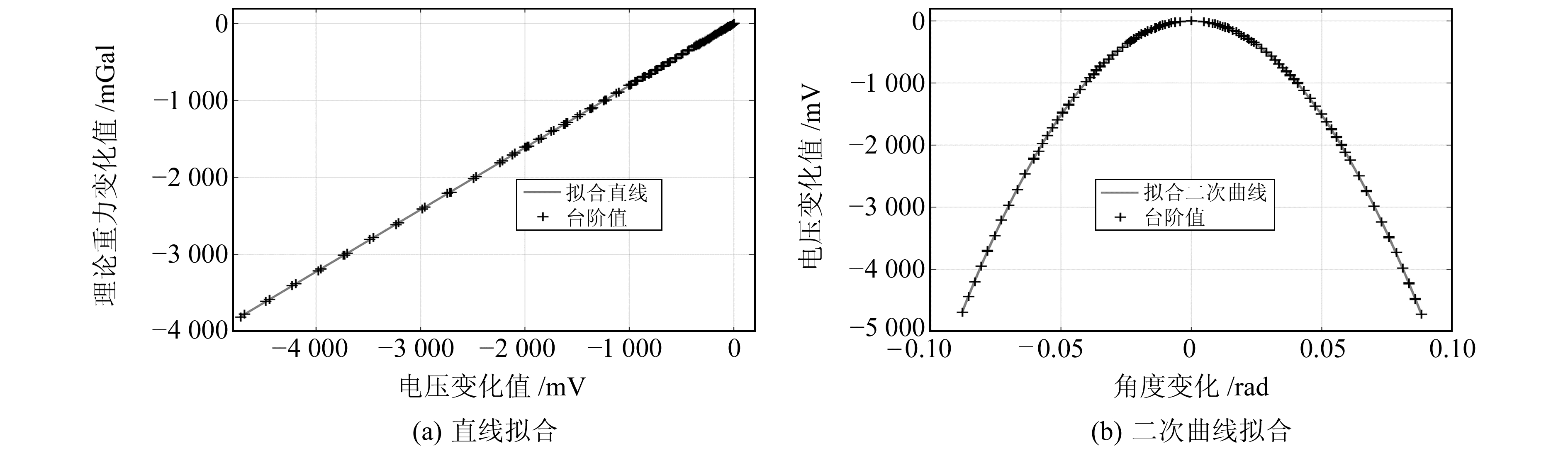
图 2和3分别展示了随着U轴倾斜和V轴倾斜带来的重力仪探头电压输出值的变化,从图中可以清晰地看到电压值台阶,每个台阶求取电压平均值作为台阶值。采用2种拟合方法求取格值,第1种方法为直线拟合,第2种方法为二次曲线拟合。采用直线拟合时,根据式(3)可知,其斜率即为所要求的格值,U轴和V轴的直线拟合结果分别见图 4(a)和5(a)。采用二次曲线拟合时,拟合电压变化值与倾角之间的二次函数,得到二次项拟合系数,再根据式(6)计算得到格值,U轴和V轴的二次曲线拟合结果分别见图 4(b)和5(b)。
|
图 2 U轴倾斜实验时间序列 Fig. 2 The time series data of U-axis tilt test |
|
图 3 V轴倾斜实验时间序列 Fig. 3 The time series data of V-axis tilt test |

|
图 4 U轴直线拟合与二次曲线拟合结果 Fig. 4 Straight line fitting and quadratic curve fitting results of U-axis |
|
图 5 V轴直线拟合与二次曲线拟合结果 Fig. 5 Straight line fitting and quadratic curve fitting results of V-axis |
表 2为拟合结果及精度统计,可以看出,U轴的拟合精度比V轴高。从理论上来说,U轴与V轴是完全对称的,其结果应该一样,这可能与敏感探头机械上的误差及六自由度平台有关。采用测量平差方法对得到的4个拟合结果进行加权平均,得到最终格值为0.806 07 mGal/mV,精度为3.6×10-5。
|
|
表 2 U轴、V轴的拟合结果及精度 Tab. 2 Fitting results and accuracy of U-axis and V-axis |
本文对重力仪生产及实践中至关重要的格值标定进行讨论,详细介绍在实验室利用六自由度平台标定国产自主研发的CHZ-Ⅱ海空重力仪,分别采用直线拟合和二次曲线拟合2种方法对实验数据进行分析,最终得到格值的加权平均值为0.806 07 mGal/mV。利用倾斜法标定格值在实验室就能完成,简单易行,但缺点是只能使重力仪敏感到的重力变小,标定重力仪读数变小方向的格值,而无法标定重力仪读数变大方向的格值。重力仪探头的倾斜与实际测量时重力仪探头在稳定平台上的测量状态是有差异的,由此也会引入一定的误差。采用倾斜法是在实验室得到的标定结果,为得到更加精确的重力仪格值,后期将在野外采用长基线法标定CHZ-Ⅱ海空重力仪。
| [1] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 信息工程大学, 2004 (Sun Zhongmiao.Theory, Method and Application of Airborne Gravimetry[D].Zhengzhou: Information Engineering University, 2004)
(  0) 0) |
| [2] |
黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005 (Huang Motao, Zhai Guojun, Guan Zheng, et al. Determination and Application of Marine Gravity Filed[M]. Beijing: Surveying and Mapping Press, 2005)
(  0) 0) |
| [3] |
梁星辉.航空重力测量方法及试验研究[D].北京: 中国科学院大学, 2012 (Liang Xinghui.Method and Experiment Research on Airborne Gravimetry[D].Beijing: University of Chinese Academy of Sciences, 2012)
(  0) 0) |
| [4] |
欧阳永忠.海空重力测量数据处理关键技术研究[D].武汉: 武汉大学, 2013 (Ouyang Yongzhong.On Key Technologies of Data Processing for Air-Sea Gravity Surveys[D].Wuhan: Wuhan University, 2013)
(  0) 0) |
| [5] |
孙中苗, 李迎春, 张松堂, 等. LaCoste&Romberg航空重力仪的格值标定[J]. 大地测量与地球动力学, 2008, 28(2): 132-135 (Sun Zhongmiao, Li Yingchun, Zhang Songtang, et al. Calibration of Scale Value for LaCoste&Romberg Airborne Gravimeter[J]. Journal of Geodesy and Geodynamics, 2008, 28(2): 132-135)
(  0) 0) |
| [6] |
华昌才, 果勇. 拉科斯特重力仪的格值标定[J]. 地震学报, 1991, 13(2): 248-253 (Hua Changcai, Guo Yong. Calibration of the Lacoste-Romberg Gravimeter[J]. Acta Seismologica Sinica, 1991, 13(2): 248-253)
(  0) 0) |
| [7] |
刘冬至, 王晓权, 邢灿飞, 等. 《2000国家重力基本网》短基线的检定与分析[J]. 大地测量与地球动力学, 2002, 22(4): 61-65 (Liu Dongzhi, Wang Xiaoquan, Xing Canfei, et al. Verification and Analysis of Short Calibration Lines of 2000 National Gravity Network[J]. Journal of Geodesy and Geodynamics, 2002, 22(4): 61-65)
(  0) 0) |
| [8] |
许时耕, 钟显煜. 海洋重力仪常数检定的新途径[J]. 地球物理学报, 1981, 24(1): 126-129 (Xu Shigeng, Zhong Xianyu. The New Way for Evaluation the Constant of the Seagravimeter[J]. Chinese Journal of Geophysics, 1981, 24(1): 126-129)
(  0) 0) |
| [9] |
黄谟涛, 刘敏, 邓凯亮, 等. 利用重复测线校正海空重力仪格值及试验验证[J]. 地球物理学报, 2018, 61(8): 3 160-3 169 (Huang Motao, Liu Min, Deng Kailiang, et al. Test and Correction of Scale Values for Air-Sea Gravimeters Using Repeated Survey Lines[J]. Chinese Journal of Geophysics, 2018, 61(8): 3 160-3 169)
(  0) 0) |
| [10] |
张善言, 李锡其, 梁础坚, 等. 新研制的CHZ海洋重力仪[J]. 测绘学报, 1987, 16(1): 1-6 (Zhang Shanyan, Li Xiqi, Liang Chujian, et al. Newly Developed CHZ Sea-Gravimeter[J]. Acta Geodetica et Cartographica Sinica, 1987, 16(1): 1-6)
(  0) 0) |
| [11] |
张善言, 宗杰. CHZ海洋重力仪的三次海上测量[J]. 测绘学报, 1988, 17(3): 73-78 (Zhang Shanyan, Zong Jie. The Three Gravity-Measurement Expeditions on Surface Boat with CHZ Seagravimeter[J]. Acta Geodetica et Cartographica Sinica, 1988, 17(3): 73-78)
(  0) 0) |
| [12] |
宗杰. CHZ重力仪在动态重力测量中的非线性问题[J]. 测绘学报, 1987, 16(1): 9-18 (Zong Jie. On the Effect of Dynamic Non-Linearity of CHZ Sea Gravimeter in Dynamic Gravity Measurement[J]. Acta Geodetica et Cartographica Sinica, 1987, 16(1): 9-18)
(  0) 0) |
| [13] |
张善言, 周东明, 宗杰, 等. 航空重力仪的实验[J]. 地球物理学报, 1990, 33(1): 70-76 (Zhang Shanyan, Zhou Dongming, Zong Jie, et al. Test of an Airborne Gravimeter[J]. Chinese Journal of Geophysics, 1990, 33(1): 70-76)
(  0) 0) |
| [14] |
Torge W. Gravimetry[M]. Berlin: Walter de Gruyter, 1989
(  0) 0) |
| [15] |
涂海波, 何建刚, 刘雷钧, 等. CHZ-Ⅱ海洋重力仪重力敏感结构的性能测试与分析[J]. 大地测量与地球动力学, 2015, 35(4): 711-714 (Tu Haibo, He Jiangang, Liu Leijun, et al. Performance Characteristics for the g-Sensitive Elastic Structure of CHZ-Ⅱ Sea Gravimeter[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 711-714 DOI:10.14075/j.jgg.2015.04.037)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40


