目前常用的自动拾取地震动P波和S波震相到时的方法主要有长短时均值比法(STA/LTA方法[1-5]和AIC准则[6-8])、高阶统计计量方法(PAI-S/K方法[9-10])及自回归方法[11],另外还有分形维法和神经网络法等[12]。
长短时均值比法是目前广泛使用的一种地震波初至拾取方法,其原理是取地震波特征函数在短时间内平均值与长时间内平均值之比确定地震波初至,即长短时均值比法,地震波初至时刻就是用长短时均值比法计算得到超过阈值的时刻。长短时均值比法具有算法简单、计算速度快和特征函数多样等优点,同时也存在不足之处:1)目前特征函数的选择与地震波震相初至定义不吻合,使得到时的拾取在理论上就不够明确;2)短时间和长时间采用的时长不明确,而不同的时长,特别是短时间时长对到时的拾取结果有重要影响;3)作为分子的短时间项包含在分母中,而短时间项的作用是反映异常,出现在分母中减弱了异常表现;4)地震震相到时阈值确定原则不够明确。本文针对以上问题提出解决方案,并通过汶川地震和芦山地震的记录验证提出的方法的有效性。
1 以振幅为特征函数拾取地震波震相目前地震波震相自动拾取常常用到长短时变换,其原理为[1-2]:
| $\begin{array}{*{20}{c}} {\left\{ {{P_i}} \right\} = \frac{{\sum\limits_{j = {N_3} - {N_i} + i}^{i + {N_3}} {{P_i}} /{N_4}}}{{\sum\limits_{j = i}^N {{P_i}} /{N_3}}}, 0 \le i \le N - 2 - {N_3}}\\ {{N_4} << {N_3} << N} \end{array} $ | (1) |
式中,Pi为与地震记录相关的特征函数,{Pi}为经过长短时变换得到的序列,i为地震记录点序号,N4为长短时均值比方法的短尺度,N3为长尺度。地震记录可以是加速度、速度和位移,由于地震加速度变化相对迅速,有利于震相的自动拾取,本文重点研究在加速度记录中拾取P波和S波震相。
利用公式(2)进行长短时变换:
| $\begin{array}{*{20}{c}} {\left\{ {{P_i}} \right\} = \frac{{\sum\limits_{j = {N_4}}^{{N_3}} {{P_i}} /{N_3} - {N_4} + 1}}{{\sum\limits_{j = i}^{i + {N_4}} {{P_i}} /{N_4}}}, 0 \le i \le N - 2 - {N_3}}\\ {{N_4} << {N_3} << N} \end{array} $ | (2) |
式(1)和式(2)中,分子为短时项,分母为长时项。式(1)中的短时项包含在长时项中,而式(2)中短时项不包含在长时项中,且短时项是作为异常项出现的,而长时项是作为正常情况下的正常项出现的,其物理意义是异常项与正常项的均值比。式(1)中分母包含了异常项,其物理意义不够明确,在相同条件下,式(2)计算得到的数值一定大于式(1)的计算结果,所以式(2)有较强的表现异常的能力。
式(2)中的分母可以是作为未发生地震时的微震动信号记录出现的,可以在地震波未到达前计算完毕,在实际应用时可以不参与运算。从这个意义上讲,该公式的分母是一个常数,当然完全可以参与实时运算,本文通过预留在地震记录中的微震动信号取10 s时长计算得到。
震相到时无论P波还是S波都定义在波峰(波谷)处,P波到时是地震记录中第一个纵波波峰(波谷)对应的时刻,S波是第一个剪切波波峰(波谷)对应的时刻。取与振幅有关的函数F为特征函数:
| $F=\left|x(t)^{n}\right| $ | (3) |
式中,X(t)为三分量加速度记录之一,n为大于或等于1的整数。与Allen[1-2]提出的特征函数相比,式(3)仅有振幅,没有振幅的变化,这是因为当振幅达到峰值时,振幅的变化并不一定大,用振幅和振幅的变化同时作为特征函数表现异常会使异常分散;式(3)也有别于何先龙等[5]的能量变化率,因为在P波或S波到达波峰(波谷)时的能量变化率未必是最大的。由式(3)可知,地震波到时就是特征函数对应的最大值,而式(2)相当于一个有异常记录点特征函数与正常情况下特征函数的比值,当有地震波输入时,该比值会明显大于1;没有地震波输入时,该比值略小于或略大于1。在实际操作中,式(3)的特征函数采用n=4的形式,小于1的数4次方后会更小,大于1的数4次方后会更大,这样地震波到达时用4次方特征函数会突出异常表现。
在式(2)中的短时间仅仅取3个数据点,长时间尽可能取较长时间,这样当短时间包含波峰(或波谷)和前后2个次极大值时,中间的峰值一定对应着震相的到时。地震波在均匀、各向同性介质中是沿直线传播的,但地壳介质为层状分布,离地面越近介质密度越小,波速也变小。按折射定律,地震波入射角正弦与波速成正比,当地震波从深部传向地表时,波速的减小会使地震波的入射角减小,使得在地表接收到的地震波都是几乎垂直地面入射的。
地震台首先接收到P波,其传播方向与震动方向平行,故只采用竖直方向记录;S波震动方向与传播方向垂直,采用东西向(xEW)和北南向(xNS)两水平方向的地震记录。先用式(4)计算水平向地震记录幅值,再用式(3)计算特征函数:
| $x(t)=\sqrt{x_{\mathrm{NS}}^{2}(t)+x_{\mathrm{EW}}^{2}(t)} $ | (4) |
拾取P波或S波到时需要确定一个触发阈值,如果长短时均值比得到的数值达到阈值,立即按时间顺序搜寻特征函数极值,极值对应的时刻就是震相到时。
拾取P波的步骤为:1)输入竖直方向的地震数据流;2)用式(3)计算特征函数(n=4);3)用式(2)进行长短时均值比(短时间取3个记录点,长时间取平时2 000个记录点);4)判定长短时均值比结果是否达到阈值,若达到则继续,否则回到步骤1);5)从长短时均值比结果达到阈值的对应时刻开始,按时间顺序寻找长短时均值比中最大值,其对应的时刻就是P波到时。拾取S波到时的步骤与拾取P波相似,读者可自行给出。
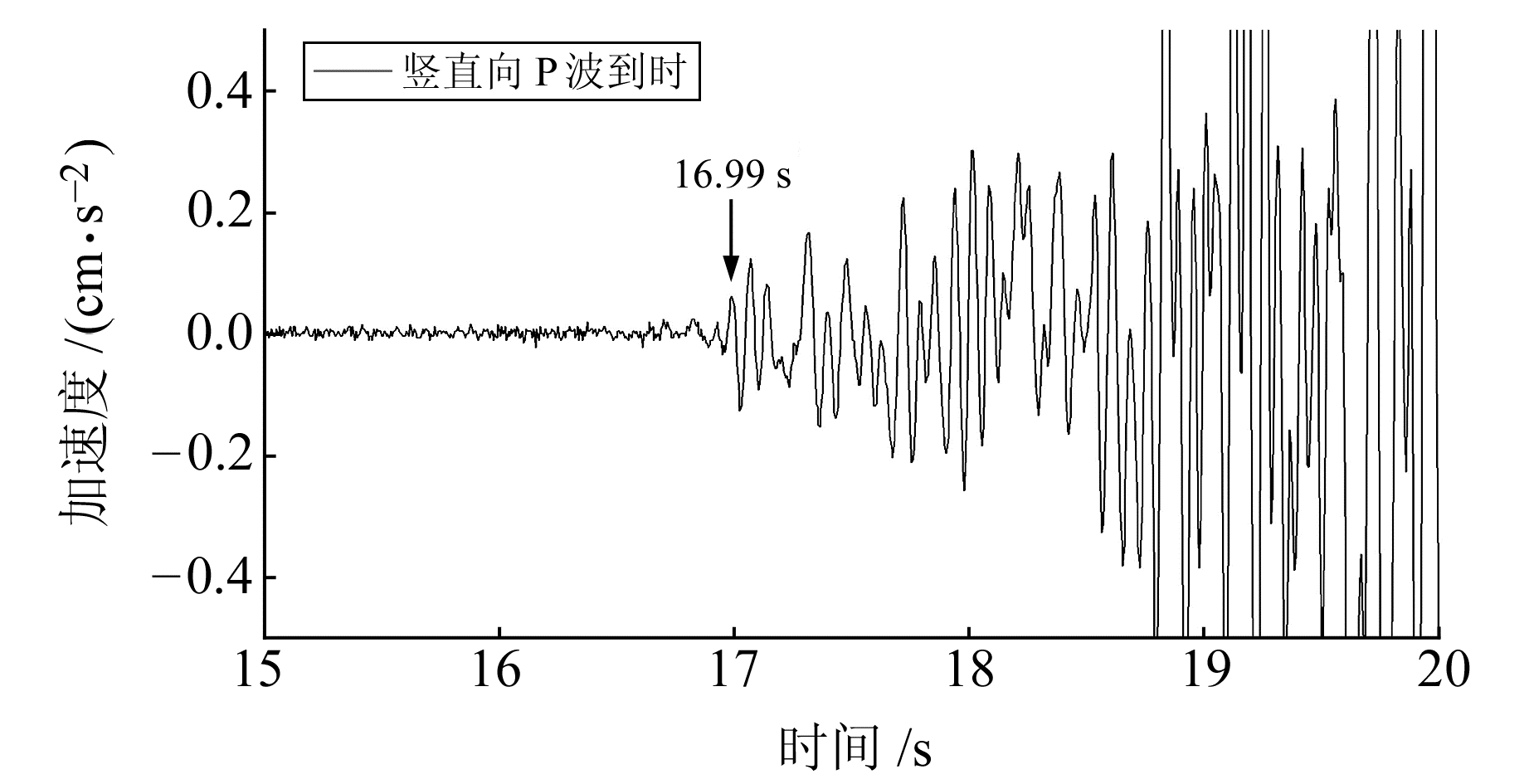
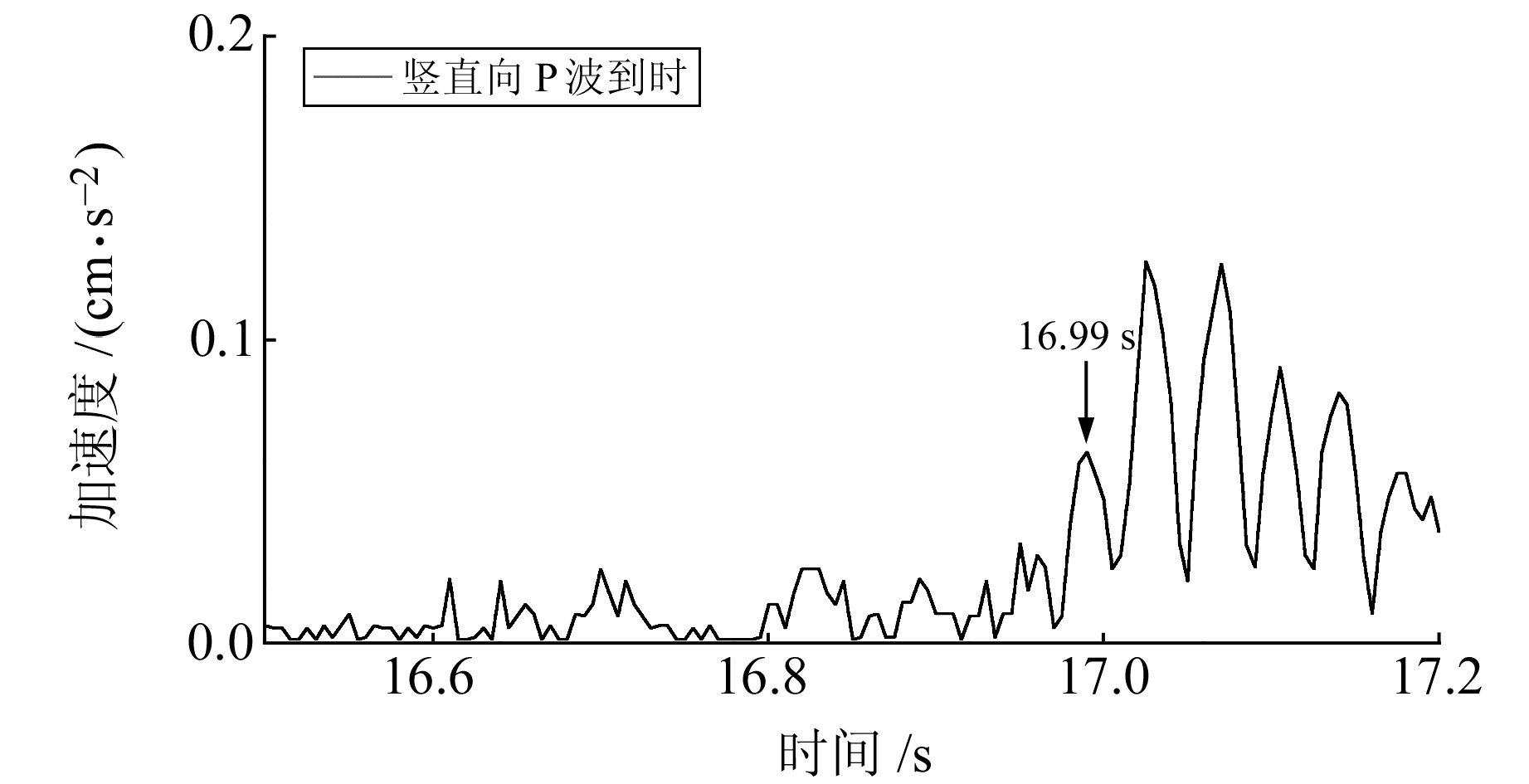
2 拾取P波到时实例图 1为汶川地震时某台站竖直方向的加速度记录,采样时间间隔为0.005 s,通过人工拾取得到P波到时为16.99 s,位于第3 398个采样点。图 2为n=1时的特征函数,图 3为n=4时的特征函数,从图 2~3可以看出,无论是1次特征函数还是4次特征函数,都清晰地反映了P波的到时均处于振幅峰值对应的时刻,但1次特征函数的P波到时峰值相对干扰差异小,4次特征函数的P波到时峰值相对干扰差异大,这就是选择4次函数作为拾取P波到时特征函数的原因之一。
|
图 1 地震加速度竖直方向记录 Fig. 1 Seismic acceleration record in vertical direction |
|
图 2 P波1次特征函数 Fig. 2 P-wave one power eigenfunction |

|
图 3 P波4次特征函数 Fig. 3 P-wave four power eigenfunction |
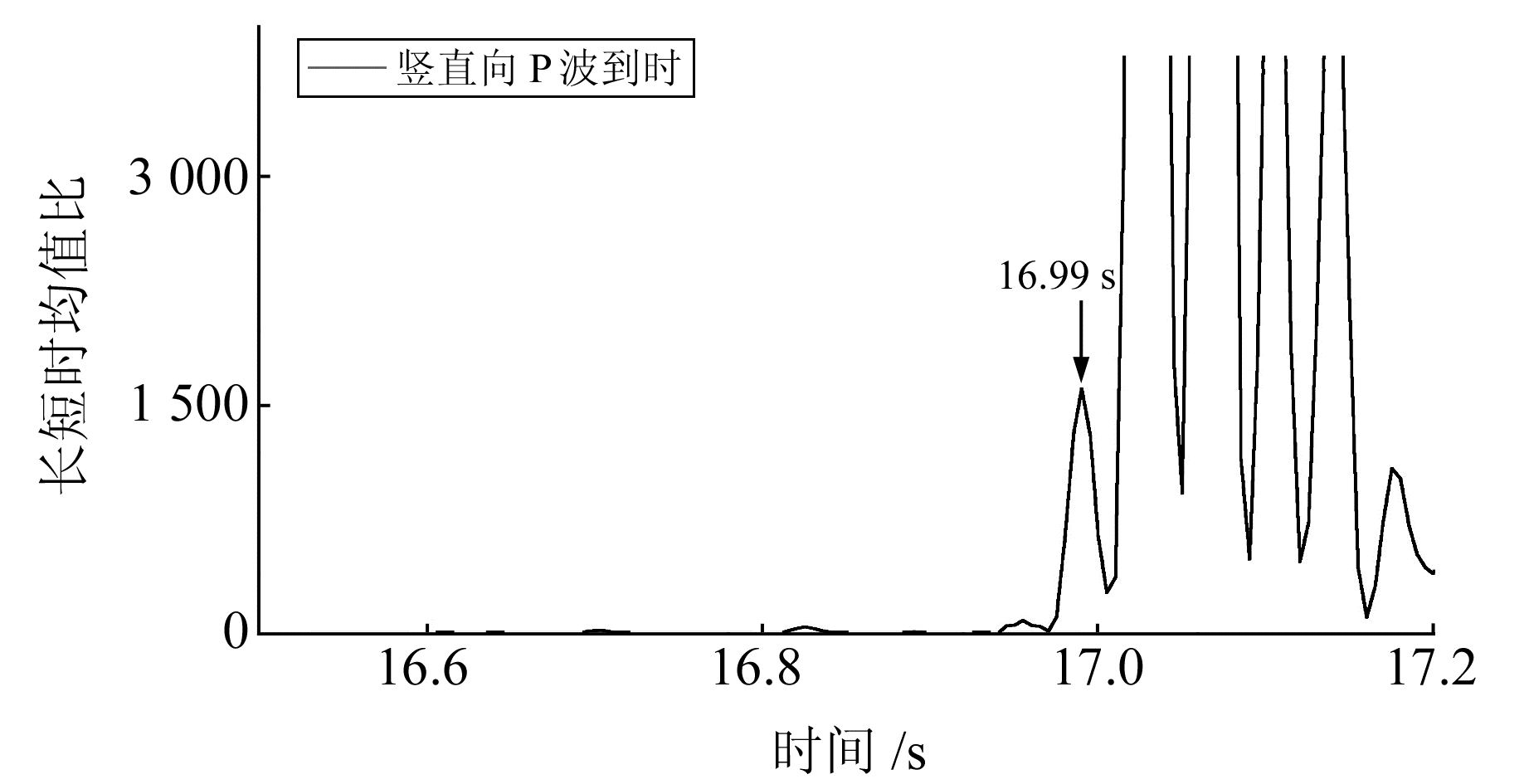
图 4为以1次函数作为特征函数(n=1)长短时均值比拾取的P波到时,图 5为以4次函数作为特征函数(n=4)长短时均值比拾取的P波到时。2个特征函数都准确地拾取了P波到时,但1次函数拾取的P波到时对应的峰值(10.101 5)与干扰波的峰值(4.373 1)差异小,两者峰值在同一数量级上,不利于确定P波到达的阈值(图 4);而4次函数拾取的P波到时对应的峰值(1 613.547 2)与干扰波的峰值(47.477 5)差异十分明显,容易确定P波到达的阈值(图 5),这也是选择4次函数作为特征函数的原因。根据图 5确定P波到时的阈值后,按时间次序搜寻长短时均值比的峰值,峰值对应的时刻就是P波到时。
|
图 4 用1次函数拾取的P波到时 Fig. 4 P-wave arrival time picked by the one power eigenfunction |

|
图 5 用4次函数拾取的P波到时 Fig. 5 P-wave arrival time picked the four power eigenfunction |
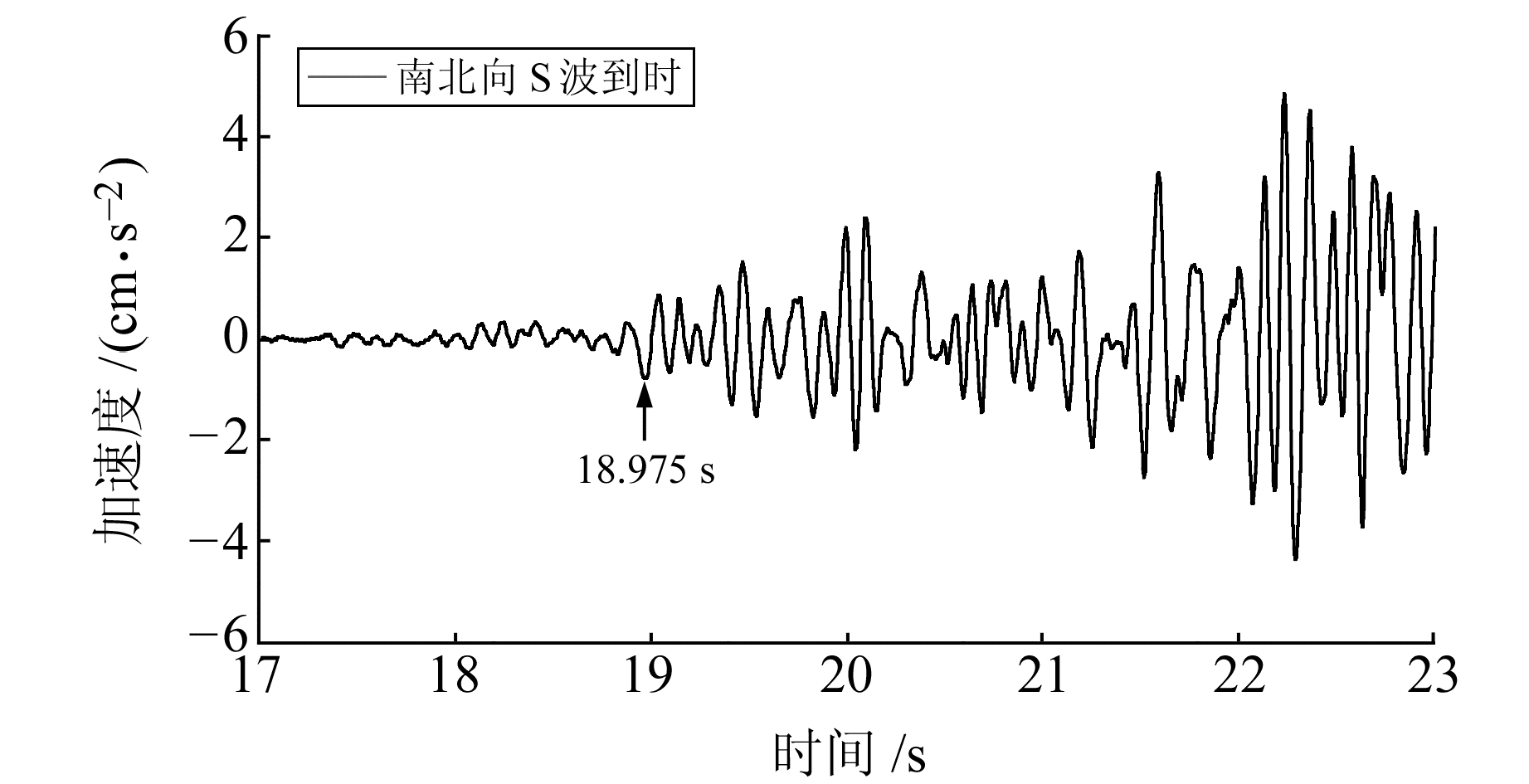
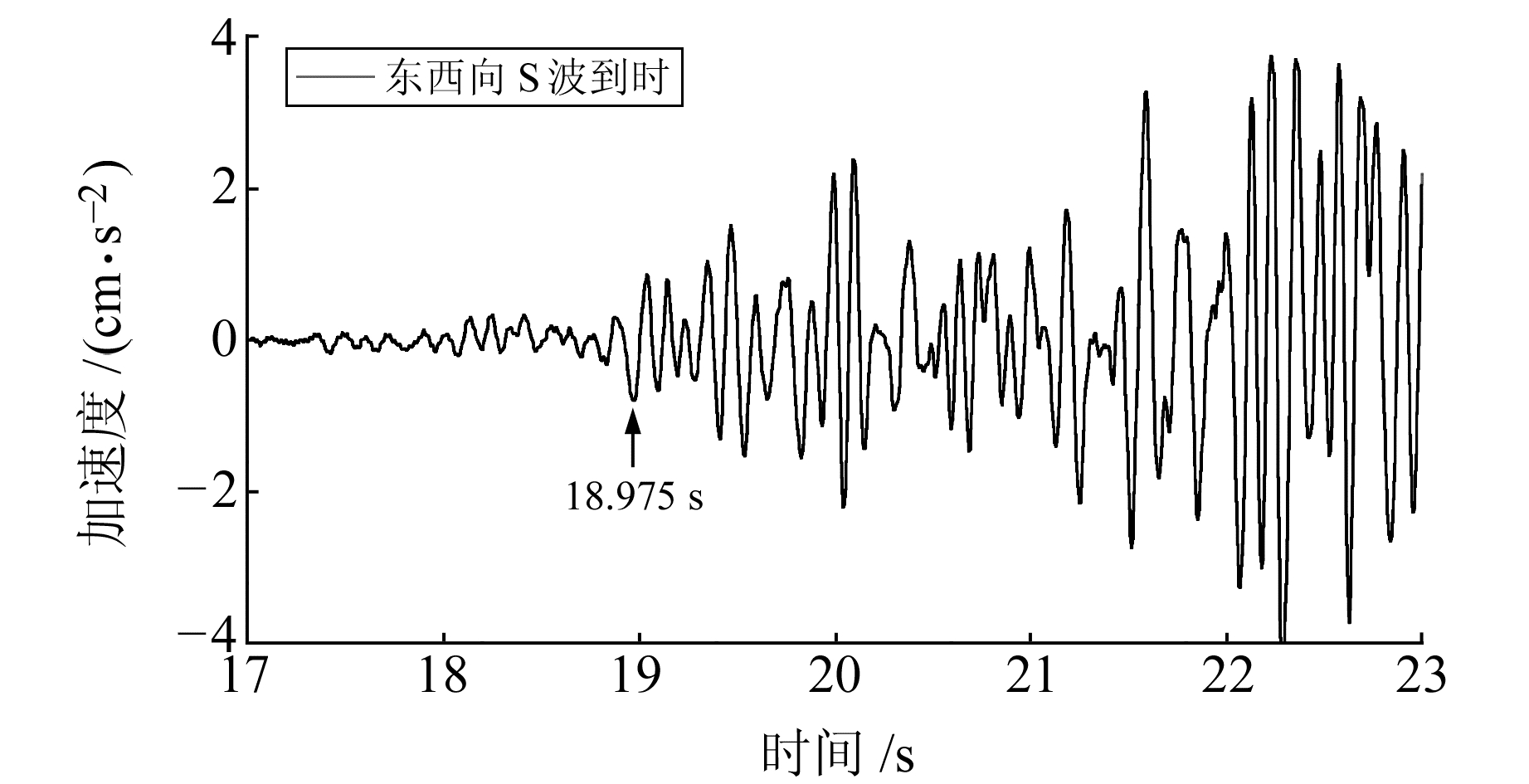
图 6为汶川地震某台站南北向的加速度记录,采样时间间隔为0.005 s,通过人工拾取得到S波到时为18.975 s,位于第3 795个采样点;图 7为该台站东西向的加速度记录,通过人工拾取得到S波到时也是18.975 s,两图的到时都对应着地震动幅值的波谷。
|
图 6 地震加速度南北向记录 Fig. 6 The seismic acceleration record in NS direction |
|
图 7 地震加速度东西向记录 Fig. 7 The seismic acceleration record in EW direction |
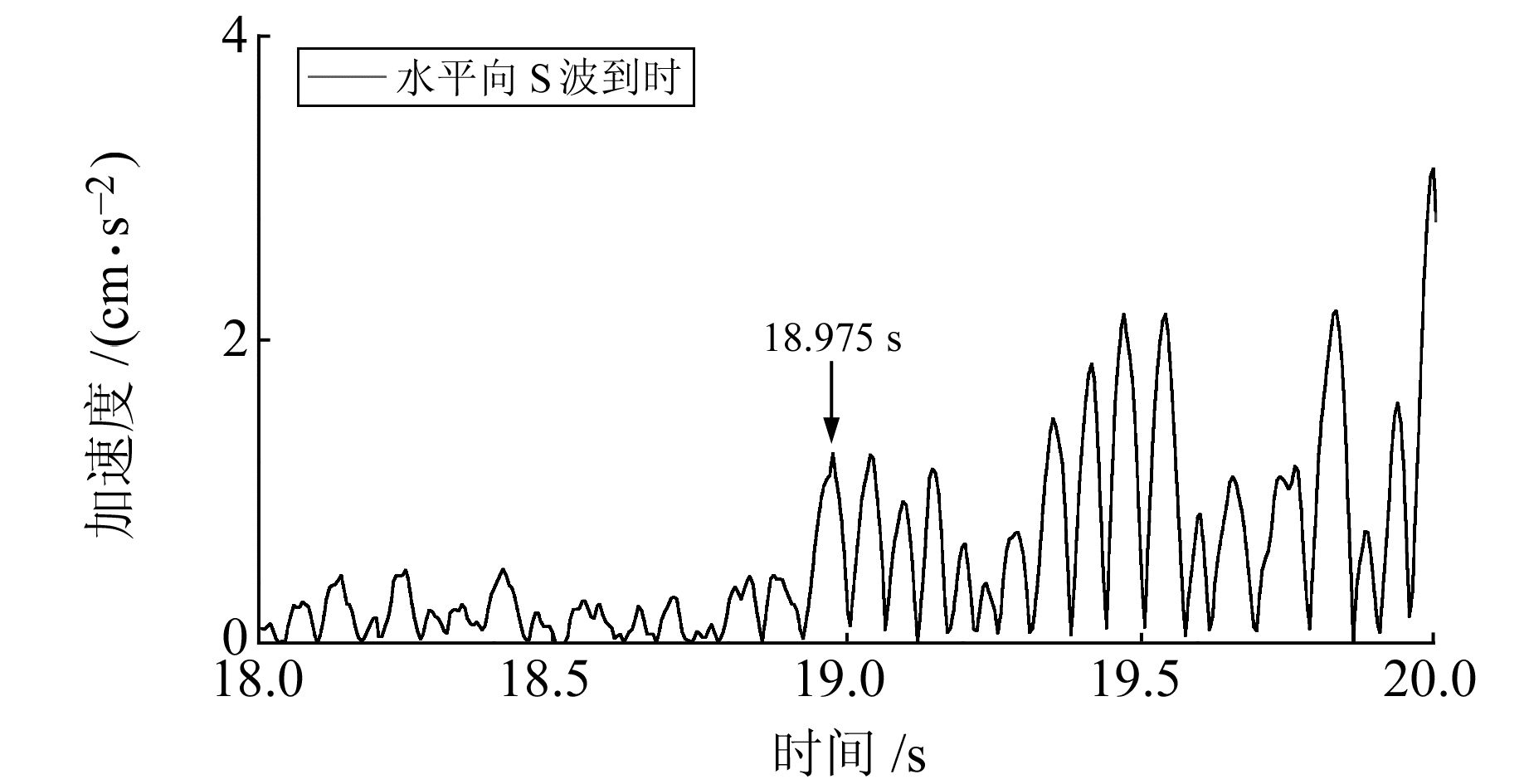
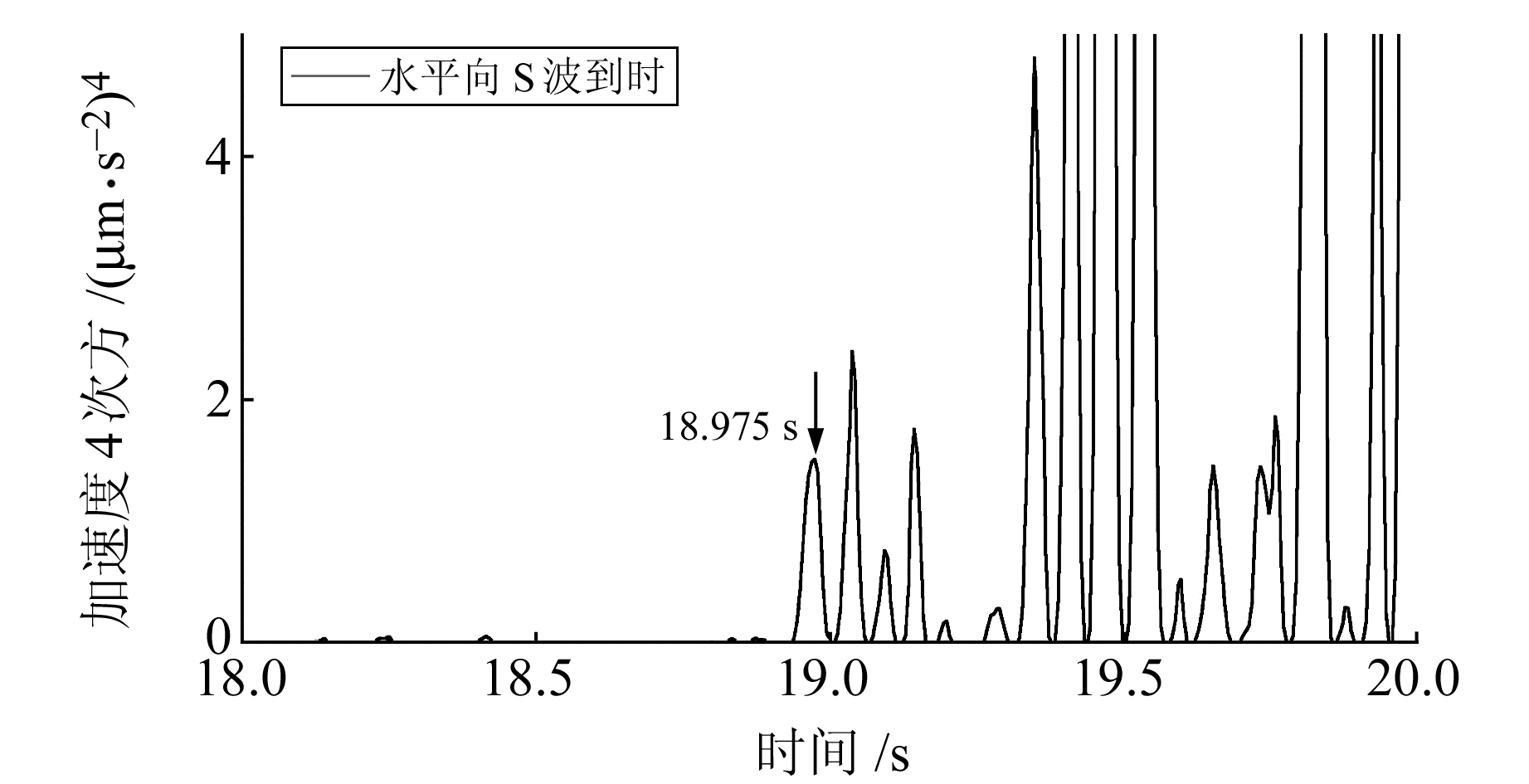
图 8为n=1时的1次特征函数,图 9为n=4时的4次特征函数。由图 8~9可以看出,无论是1次特征函数还是4次特征函数,都清晰地反映了S波的到时处于振幅峰值对应时刻,但1次特征函数的S波到时峰值相对干扰差异小,而4次特征函数的S波到时峰值相对噪声差异大。4次特征函数放大了有地震波输入时的异常,这就是选择4次函数作为拾取S波到时特征函数的原因之一。
|
图 8 S波1次特征函数 Fig. 8 S-wave one power eigenfunction |
|
图 9 S波4次特征函数 Fig. 9 S-wave four power eigenfunction |
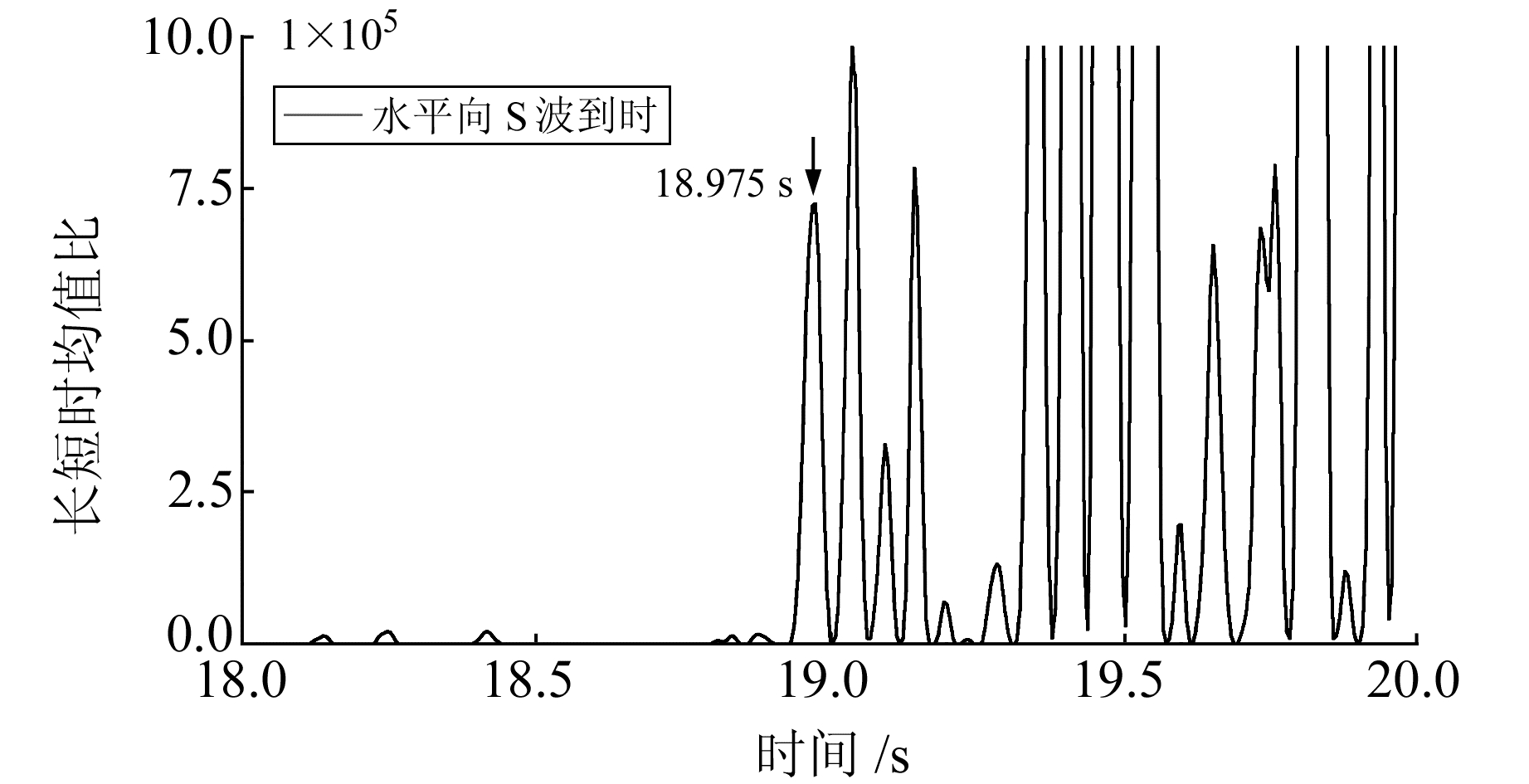
图 10为以1次函数作为特征函数长短时均值比拾取的S波到时,图 11为以4次函数作为特征函数长短时均值比拾取的S波到时。2个特征函数都准确地拾取了S波到时,均位于峰值对应的时刻,但1次函数拾取的S波到时对应的峰值(1.252 3)与干扰波的峰值(0.451 1)差异相对较小,在3倍左右;而4次函数拾取的S波到时对应的峰值(1.519 3)与干扰波的峰值(0.042 7)差异十分明显,接近40倍,容易确定S波到达的阈值,从而拾取到时,这也是选择4次函数作为特征函数的另外一个原因。根据图 11确定S波到时的阈值后,按时间次序搜寻长短时均值比的峰值,峰值对应的时刻就是S波到时。

|
图 10 用1次特征函数拾取的S波到时 Fig. 10 S-wave arrival time picked by the one power eigenfunction |
|
图 11 用4次特征函数拾取的S波到时 Fig. 11 S-wave arrival time picked by the four power eigenfunction |
拾取P波和S波到时还有一个关键问题,就是阈值的选择问题,这在一定程度上决定了拾取的成败。将要拾取的P波或S波称为有效波,其对应的长短时均值比的第一个峰值称为阈值上限;在有效波之前到达的波称为干扰波,其对应的长短时均值比的最大值称为阈值下限。阈值的确定取决于有效波和干扰波峰值的差异,差异越大越容易确定阈值。
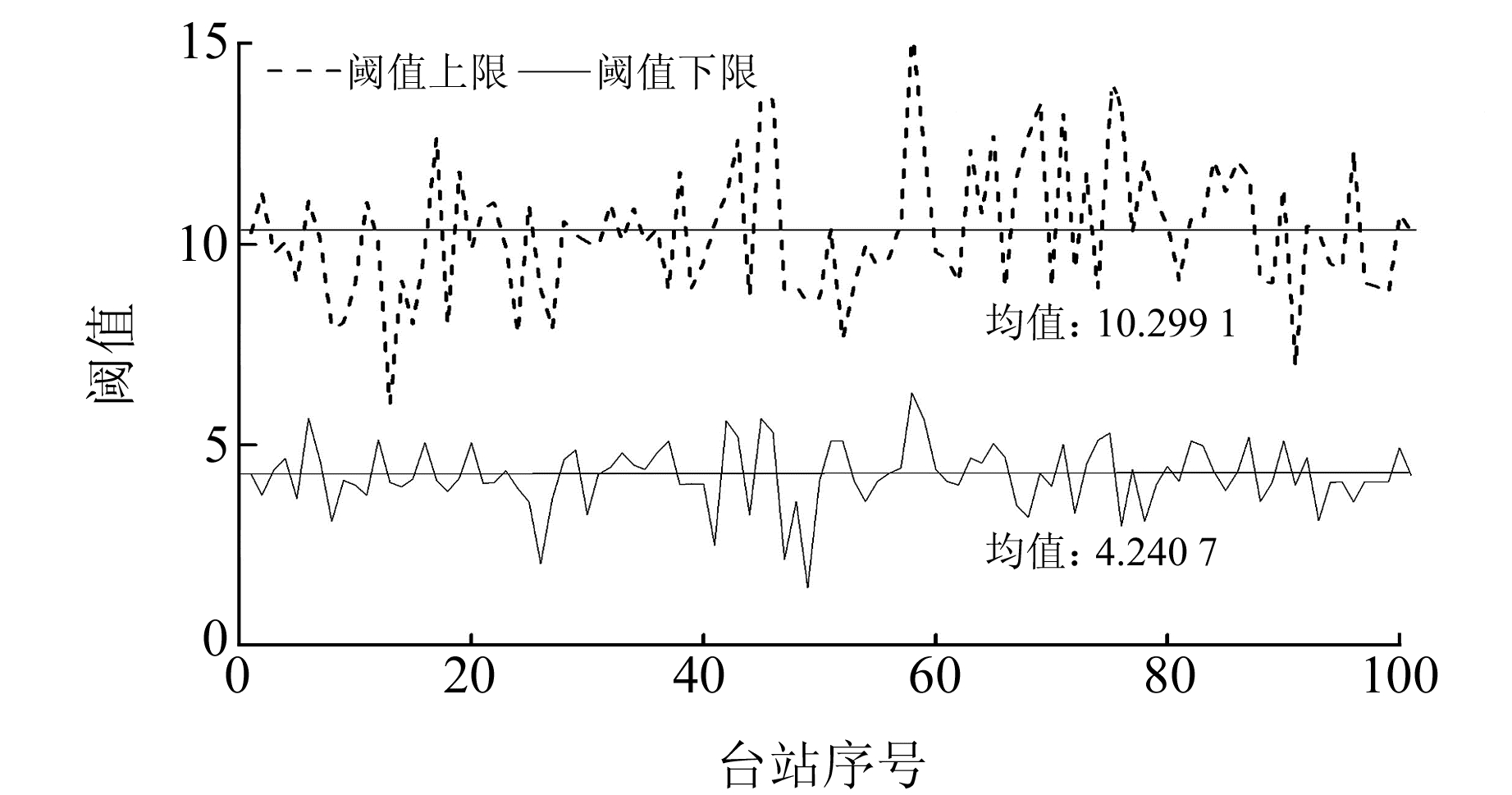
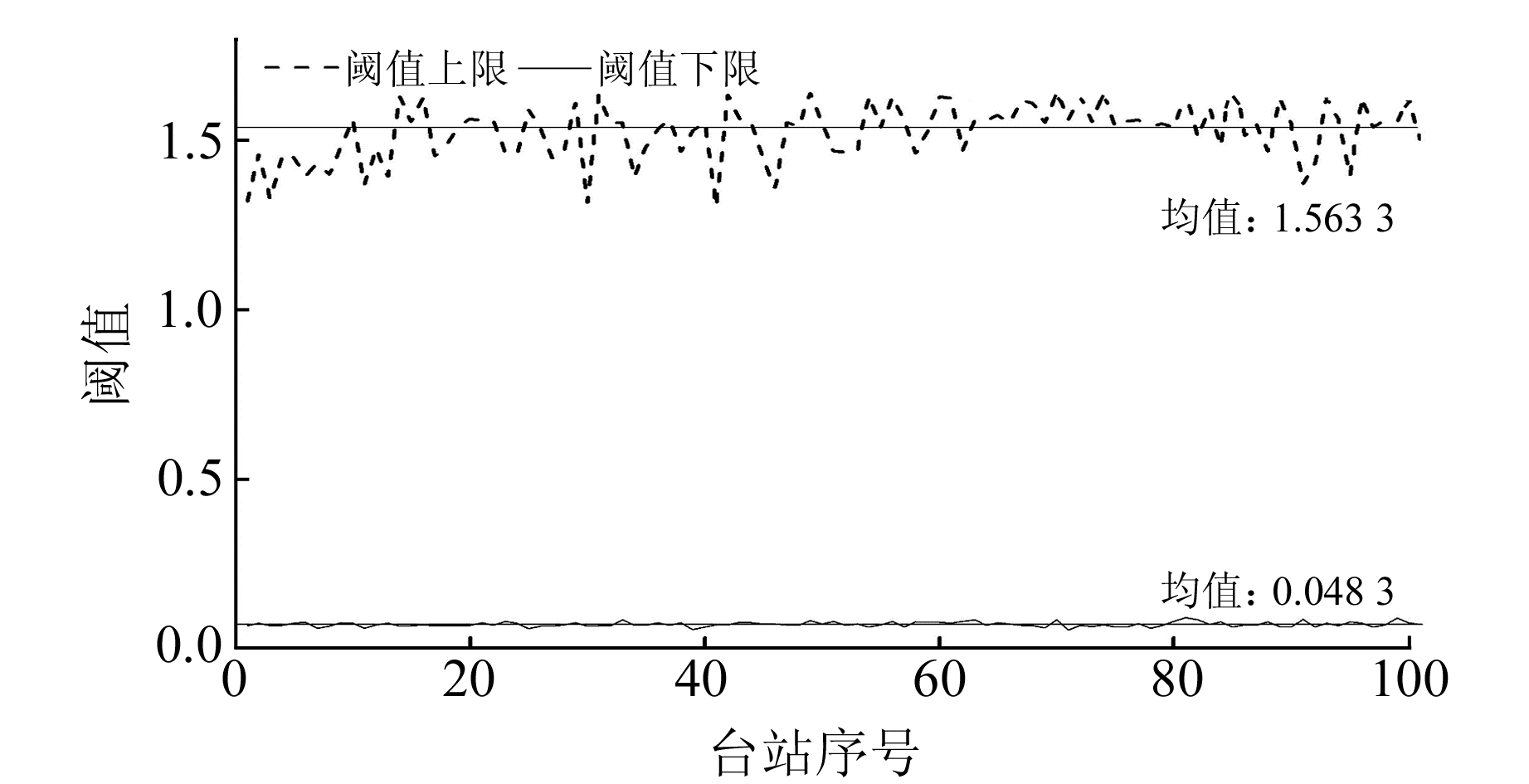
选用人工可以拾取到的汶川地震和芦山地震的100条记录,分别用1次函数和4次函数作为特征函数,用长短时均值比法拾取P波和S波到时,得到阈值上下限。图 12为1次特征函数拾取P波到时得到的阈值上下限,可以看出,P波到时阈值的上下限存在一定差异,其上限平均值为10.299 1,下限平均值为4.240 7,但两者有部分交叉,从中确定一个P波的触发阈值比较困难。图 13为4次特征函数拾取P波到时得到的阈值上下限,其上限平均值为1.563 3,下限平均值为0.048 3,两者差异明显,本文暂定拾取P波到时阈值为下限阈值的2倍,约为0.01。
|
图 12 用1次特征函数拾取P波得到的阈值 Fig. 12 Threshold obtained by picking P-waves with one power eigenfunction |
|
图 13 用4次特征函数拾取P波得到的阈值 Fig. 13 Threshold obtained by picking P-waves with the four power eigenfunction |
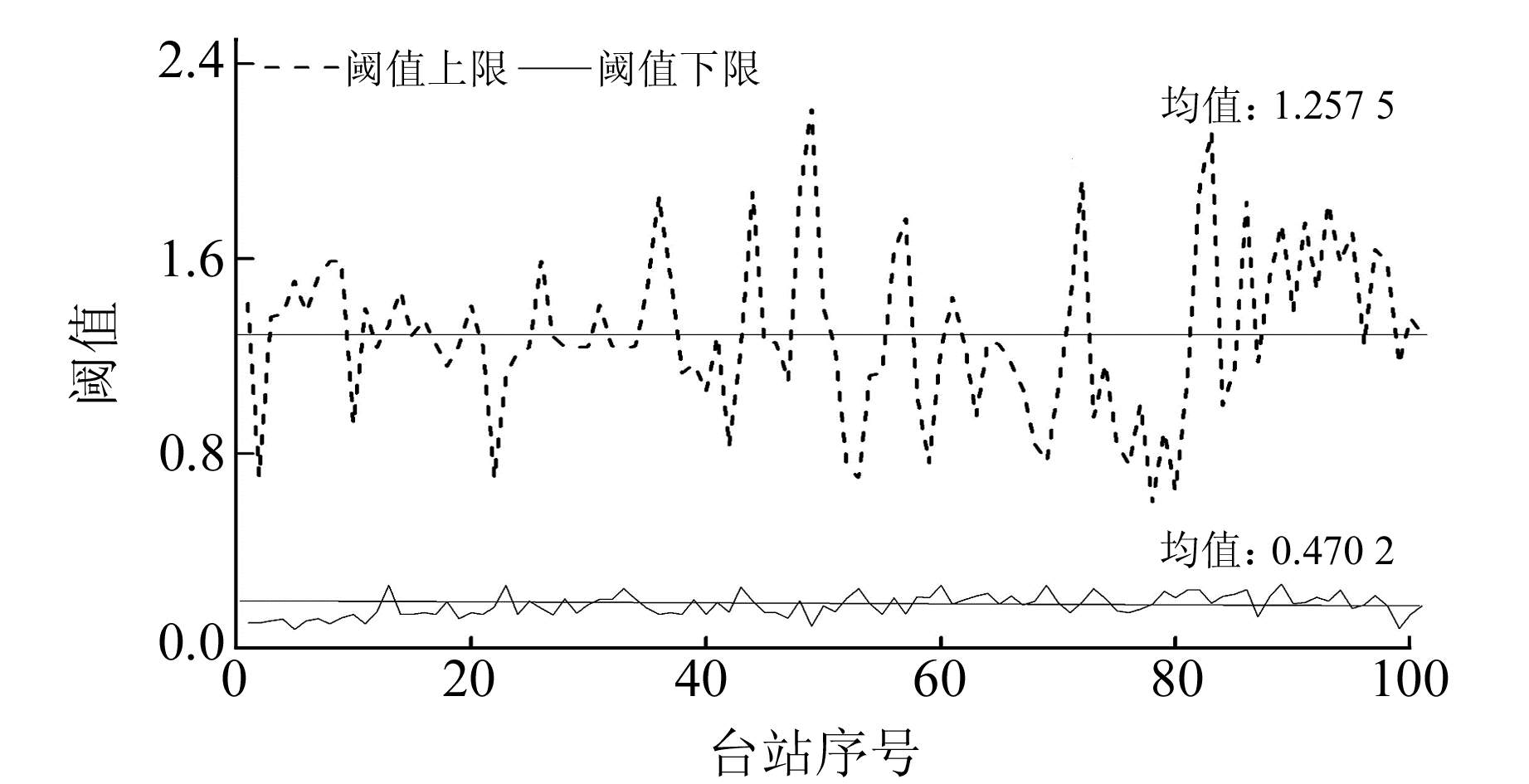
图 14为1次特征函数拾取S波到时得到的阈值上下限,其上限平均值为1.257 5,下限平均值为0.470 2,两者差异不明显。图 15为4次特征函数拾取S波到时得到的阈值上下限,其上下限差异明显,上限平均值为1.212 6,下限平均值为0.042 7,两者差异十分明显,相差2个数量级。本文暂定拾取S波到时阈值为下限阈值的2倍,约为0.1。
|
图 14 用1次特征函数拾取S波得到的阈值 Fig. 14 The threshold obtained by picking S-waves with the one power eigenfunction |

|
图 15 用4次特征函数拾取S波得到的阈值 Fig. 15 The threshold obtained by picking S-waves with the four power eigenfunction |
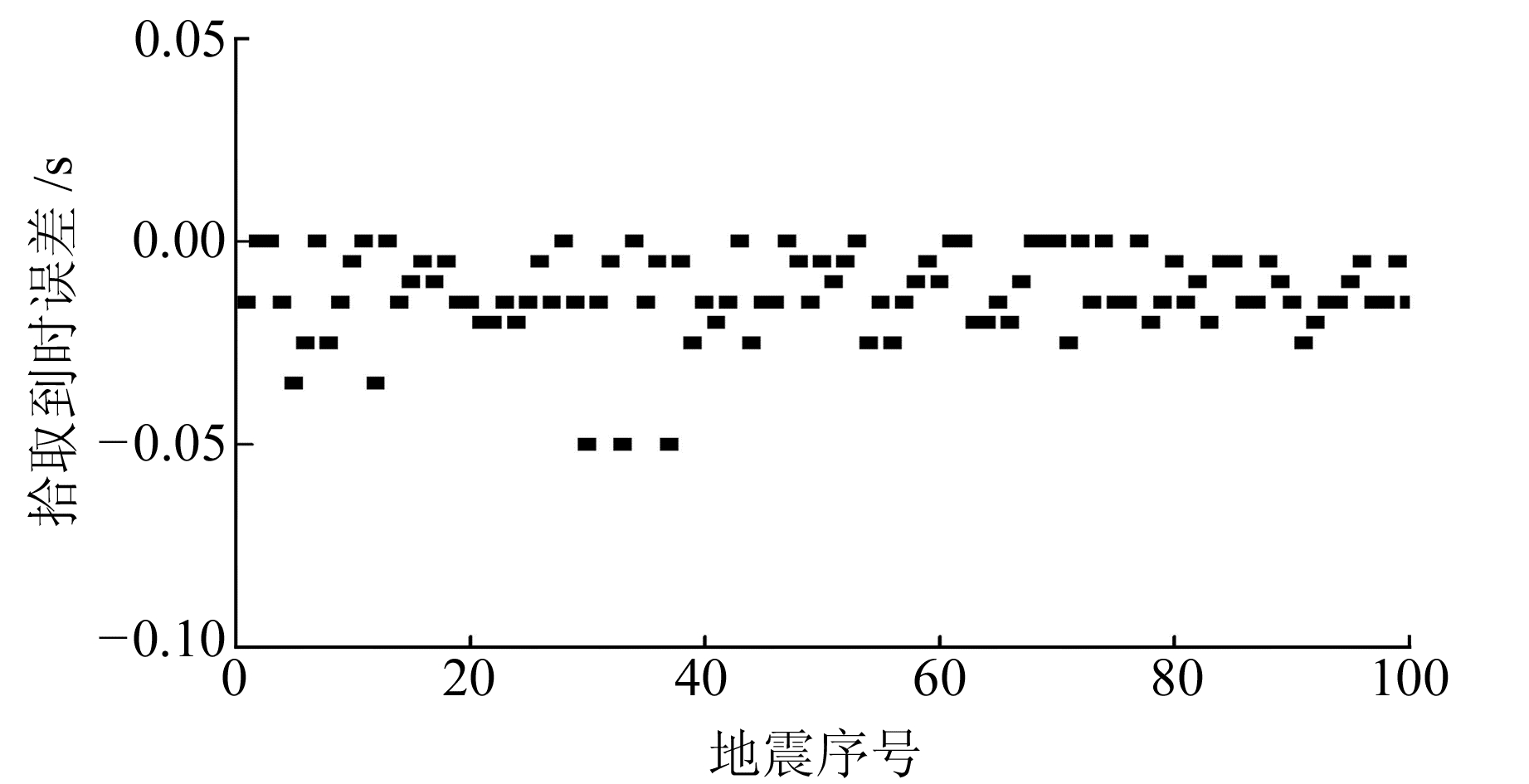
选取100个汶川和芦山MS4.0以上地震,以人工拾取的P波和S波到时作为标准,用改进的方法分别拾取P波和S波到时,拾取P波的绝对误差曲线见图 16,拾取S波的绝对误差曲线见图 17。当拾取的震相早于标准值时,误差为负,否则为正。
|
图 16 拾取P波震相到时误差 Fig. 16 Arrival time error of P-wave phase |
|
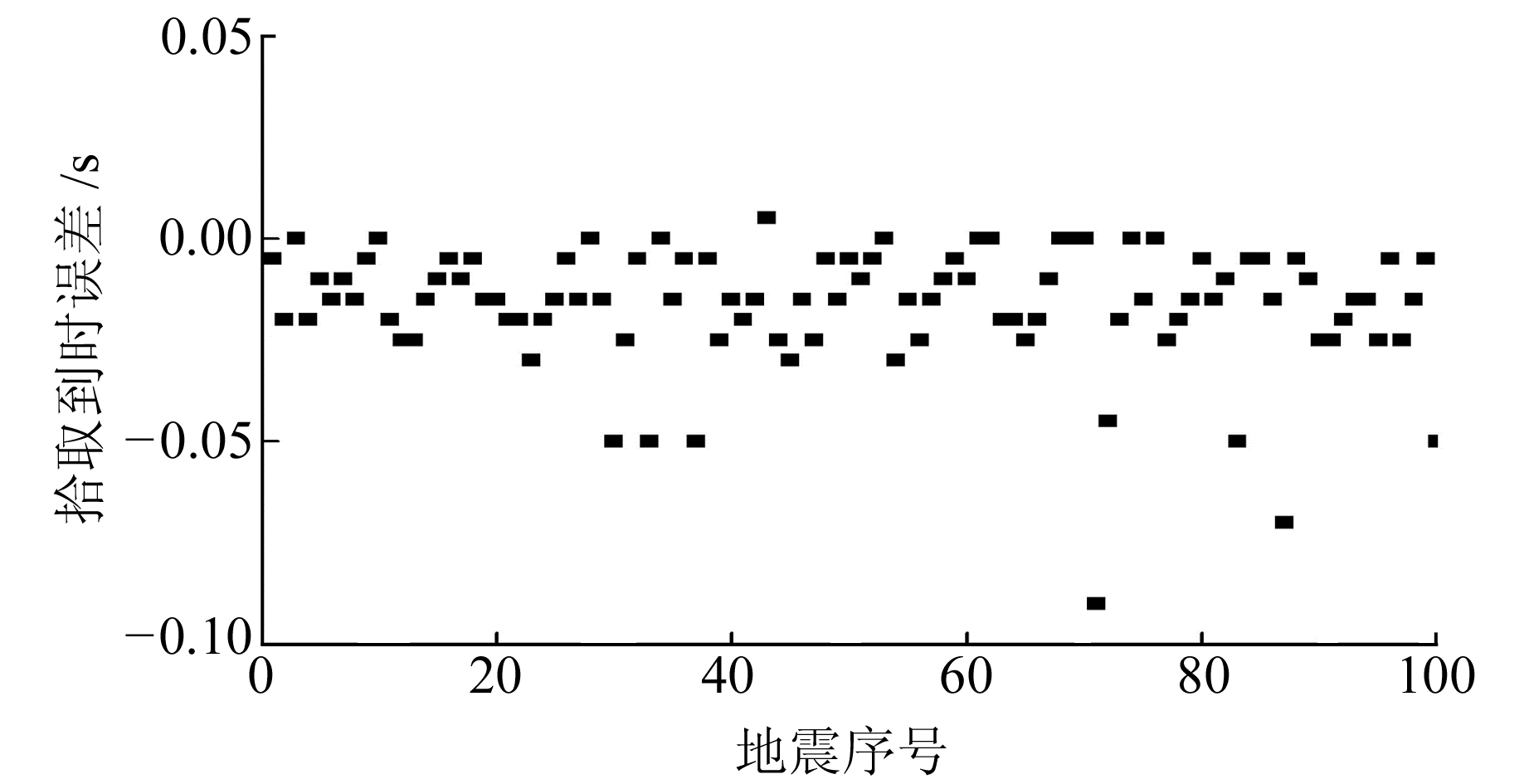
图 17 拾取S波震相到时误差 Fig. 17 Arrival time error of S-wave phase |
从图 16和17可以看出,P波拾取误差略小,并且无论P波还是S波,拾取的误差全部为负或等于0,说明拾取的到时均不晚于标准值。这是因为定义震相到时为波峰(波谷)对应的时刻,长短时均值比超过阈值后,在搜取到需要的极大值时,遇到了小的波峰(或波谷),但不可能超过需要的极大值对应的到时。波峰(波谷)对应的时刻定义为震相到时,但实际上,在波峰(波谷)到达前地震波已经到达,因此没必要过分强调拾取到时的准确性,只要误差在一定范围内工作就是有意义的。
6 结语本文对长短时均值比方法进行了改进,使其拾取地震波震相的准确度更高,并通过震例验证,得出以下结论:
1) 目前长短时均值比法中分子作为有地震输入的异常项,分母作为正常项,但分母中也包含了异常项,这使得该方法表现异常的能力不强。改进方法的异常项不出现在分母中,其长短时均值比就是异常项与正常项的比,明确了长短时均值比法的物理意义,改变了目前该方法物理意义不清的问题,明显增强了长短时均值比法表现异常的能力。
2) 震相的到时都是定义在波峰(波谷)处对应的时刻,以往特征函数的选择与定义脱节,不能反映震相到时特征,使得震相拾取的准确度降低。改进的方法用与振幅有关的函数作为特征函数,使得拾取震相到时的问题变成寻找特征函数极值的问题。
3) 分别用振幅1次方和振幅4次方作为特征函数,利用长短时均值比法拾取地震波到时,将拾取的有效波的第一个峰值定义为到时阈值的上限,干扰波的最大峰值定义为阈值下限。无论拾取P波还是S波,4次特征函数拾取结果的上下限都具有相对明显差异,说明采用4次特征函数的形式增强了异常表现,因此在工作中定义阈值为下限阈值的2倍。
4) 根据折射定律及地层介质的分布规律,地震波从深部发出将垂直入射到地面,P波在竖直方向有明显的分量,故用竖直方向的记录拾取P波;S波在水平方向有明显分量,故用东西向和南北向的记录共同拾取S波。
致谢: 感谢中国地震局工程力学研究所提供数据支持。
| [1] |
Allen R V. Automatic Earthquake Recognition and Timing from Single Races[J]. Bulletin of the Seismological Society of America, 1978, 68(5): 1 521-1 532
(  0) 0) |
| [2] |
Allen R V. Automatic Phase Pickers:Their Present Use and Future Prospects[J]. Bulletin of the Seismological Society of America, 1982, 72(6B): 225-242
(  0) 0) |
| [3] |
Jones J P, Baan M. Adaptive STA-LTA with Outlier Statistics[J]. Bulletin of the Seismological Society of America, 2015, 105(3): 1 606-1 618 DOI:10.1785/0120140203
(  0) 0) |
| [4] |
田优平, 赵爱华. 基于小波包和峰度赤池信息量准则的P波震相自动识别方法[J]. 地震学报, 2016, 38(1): 71-85 (Tian Youping, Zhao Aihua. Automatic Identification of P-Phase Based on Wavelet Packet and Kurtosis-AIC Method[J]. Acta Seismologica Sinica, 2016, 38(1): 71-85)
(  0) 0) |
| [5] |
何先龙, 佘天莉, 高峰. 一种地震P波和S波初至时间自动拾取的新方法[J]. 地球物理学报, 2016, 59(7): 2 519-2 527 (He Xianlong, She Tianli, Gao Feng. A New Method for Picking up Arrival Times of Seismic P and S Waves Automatically[J]. Chinese Journal of Geophysics, 2016, 59(7): 2 519-2 527)
(  0) 0) |
| [6] |
Akaike H.Information Theory and an Extension of the Maximum Likelihood Principle[C].2nd International Symposium on Information Theory, Budapest, 1973
(  0) 0) |
| [7] |
Maeda N. A Method for Reading and Checking Phase Time in Auto-Processing System of Seismic Wave Data[J]. Zisin, 1985, 38(3): 365-379 DOI:10.4294/zisin1948.38.3_365
(  0) 0) |
| [8] |
王继, 陈九辉, 刘启元, 等. 流动地震台阵观测初至震相的自动检测[J]. 地震学报, 2006, 28(1): 42-51 (Wang Ji, Chen Jiuhui, Liu Qiyuan, et al. Automatic Onset Phase Picking for Portable Seismic Array Observation[J]. Acta Seismologica Sinica, 2006, 28(1): 42-51 DOI:10.3321/j.issn:0253-3782.2006.01.006)
(  0) 0) |
| [9] |
Saragiotis C D. PAI-S/K:A Robust Automatic Seismic P Phase Arrival Identification Scheme[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(60): 1 395-1 404
(  0) 0) |
| [10] |
刘劲松, 王赟, 姚振兴. 微地震信号到时自动拾取方法[J]. 地球物理学报, 2013, 56(5): 1 660-1 666 (Liu Jinsong, Wang Yun, Yao Zhenxing. On Micro-Seismic First Arrival Identification:A Case Study[J]. Chinese Journal of Geophysics, 2013, 56(5): 1 660-1 666)
(  0) 0) |
| [11] |
Sleeman R, Eck T. Robust Automatic P-Phase Picking:An On-Line Implementation in the Analysis of Broad-Band Seismogram Recording[J]. Physics of the Earth and Planetary Interiors, 1999, 113(1-4): 265-275 DOI:10.1016/S0031-9201(99)00007-2
(  0) 0) |
| [12] |
刘伊克, 常旭, 王辉, 等. 三维复杂地形近地表速度估算及地震层析静校正[J]. 地球物理学报, 2001, 44(2): 272-278 (Liu Yike, Chang Xu, Wang Hui, et al. Estimation of Near-Surface Velocity and Seismic Tomographic Static Corrections[J]. Chinese Journal of Geophysics, 2001, 44(2): 272-278 DOI:10.3321/j.issn:0001-5733.2001.02.015)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

