2. 中国地震局第一监测中心,天津市耐火路7号,300180
核幔边界起伏能反映地球内部动力学的一些性质,对地球内部动力学机制及地球重力学等研究具有重要意义。由于早期的地震学数据全球覆盖范围有限,地震学方法得到的核幔边界起伏结果差异较大,由扰动位计算核幔起伏,简单地选取某几阶位系数也不尽合理。
本文利用2个较新的地震S波层析模型,采用数值法求解瞬态地幔热对流问题,得到对流的应力场和速度场,进而计算核幔边界起伏,所得结果与Morelli等[1]及Yoshida[2]运用早期模型Smean和S20RTS的计算结果比较一致,可以为核幔边界起伏的确定提供参考。
1 理论及方法 1.1 由瞬态地幔对流问题计算核幔边界起伏为简化计算,假定地幔流体为不可压缩的牛顿流体,地幔密度异常源于温度异常[3-5]。在布辛涅斯克近似下,瞬态地幔热对流满足的质量守恒方程和动量守恒方程的无量纲形式为[5-7]:
| $ {\nabla u = 0} $ | (1) |
| $ \begin{array}{*{20}{c}} { - \nabla p + \nabla \left[ {\eta \left( {\nabla u + {\nabla ^{\rm{T}}}u} \right)} \right] - }\\ {\left( {\delta \rho {g_0} + {\rho _0}\delta g} \right){\mathit{\boldsymbol{e}}_r} = 0} \end{array} $ | (2) |
式中,
式(1)和(2)组成偏微分方程组,采用数值法求解,给定地幔密度异常和地幔粘度结构,结合上、下边界的自由滑动边界条件,可以求得流体的径向约化应力σrr[2]:
| $ \sigma_{m}=-p+2 \eta\left(\frac{\partial u_{r}}{\partial r}\right) $ | (3) |
式中,ur为径向速度。核幔边界起伏δh由式(4)确定[5]:
| $ \delta h=\frac{\sigma_{rr}- <\sigma_{r}>}{\Delta \rho_{c} g} $ | (4) |
式中,< σrr>为核幔边界上σrr的平均值,Δρc为通过核幔边界,地幔与地核的密度差,取值4.4×103 kg/m3。
1.2 地幔密度异常一般可通过地震波速异常转换得到地幔密度异常。对于S波速度异常,本研究中采用2个较新的S波层析模型SEMUCB_WM1和S40RTS,将波速异常转换为地幔密度异常[8-9]。SEMUCB_WM1是采用较精确的数值地震波场数据建立的横向分辨率为1°的S波速异常层析模型。本文提取该模型中从地表到核幔边界沿半径近似平均分布的20层不同深度处的S波速度异常。S40RTS模型是利用瑞利波频散数据、远震走时数据及简正模分裂函数测量数据发展而来的地幔剪切波速度异常模型。类似地,提取该模型从地表到核幔边界处21层S波速度异常。
本研究中采用的由S波波速异常转换为地幔密度异常的关系式如下[10-11]:
| $ \frac{\delta \rho}{\rho}=c \cdot \frac{\delta v_{s}}{v_{s}} $ | (5) |
式中,c为转换因子。研究表明,随深度变化的转换因子对数值模拟地幔对流的影响比采用不同的S波层析模型的影响小得多[12-13]。因此,本文采用Ghosh等[12]的全地幔中的常数转换因子0.25。
1.3 地幔粘度结构地幔的粘度是地幔对流研究中影响较大的物理量,由于地幔内部复杂的物理化学状态,地幔粘度是一个与深度、温度及压力等相关的量。本文将地幔粘度分为径向粘度和横向粘度分别考虑。
根据目前的研究,从地表到核幔边界可将径向粘度划分为5层结构:0~100 km为岩石圈;100~200 km为软流圈;200~410 km为上地幔;410~660 km为过渡带;660~2 871 km为下地幔[5, 14]。由于地幔对流在上、下界面上的动力地形对各粘度层的绝对粘度不敏感[2],将上地幔粘度作为参考粘度ηref,取值1021Pa·s[15],其他各层对上地幔粘度的粘度比Δη(d)(≡η(d)/ηref,d为深度)分别记为Δηlith、Δηasth、Δηupmn(=1)、Δηtrzn及Δηlwmn。根据已有的关于地幔粘度结构的研究[10, 16],设定Δηlith=30为大洋岩石圈粘度值,Δηasth=0.1,Δηtrzn=0.5。鉴于目前对地幔粘度的认识还存在很多不确定,根据已有研究,将下地幔粘度Δηlwmn分别设置为40、50、60、70,模拟计算2个层析模型所对应的核幔边界起伏[17-18]。文中采用的径向粘度结构如图 1所示。

|
图 1 采用的径向粘度结构 Fig. 1 Radial viscosity structure |
对于地幔的横向粘度结构,采用2种方式设定。鉴于岩石圈中较弱的板块边界及不同地质年龄的克拉通结构,岩石圈中的横向粘度结构设置如下:假定大洋岩石圈粘度为参考值1,则板块边界两侧各2°范围的粘度设置为0.1,显生宙大陆岩石圈粘度设置为1.5,前寒武纪大陆岩石圈的粘度设置为10[6, 16],如图 2所示。

|
M、OL、Ph、PC分别表示板块边界、海洋岩石圈、显生宙大陆岩石圈、前寒武纪大陆岩石圈 图 2 岩石圈中的横向粘度结构 Fig. 2 The lateral viscosity structure of the lithosphere |
由于地幔粘度与温度的密切相关性,对于岩石圈之下的地幔,采用随温度变化的横向粘度结构[19-21],关系式如下:
| $ \eta=\eta_{0}(d) \exp \left(-E\left(T-T_{r}\right)\right) $ | (6) |
式中,E为粘度对温度的依赖程度,Tr=0.5为无量纲的参考温度,T为地幔温度。根据已有研究,采用的粘度对温度依赖程度E的值为6.9,使粘度能随温度变化3个数量级[16, 22]。
2 核幔边界起伏的数值模拟采用有限元求解代码CitcomS进行数值法求解瞬时地幔对流偏微分方程组。CitcomS是用C语言写成的、用有限元方法求解三维球坐标系下的地幔对流控制方程组的开源软件包[20, 23],获取网址为https://geodynamics.org/cig/software/citcoms/。
给定如上所述地幔密度异常及地幔粘度结构,结合上、下边界的自由滑动边界条件,能够求解瞬时地幔热对流问题,最终计算核幔边界起伏。由于地幔粘度结构的不确定性,将下地幔粘度分别设置为上地幔的40、50、60、70倍,2个层析模型对应的核幔边界起伏模拟结果如图 3所示。

|
自上到下分别对应于下地幔对上地幔的相对粘度值40、50、60、70 图 3 由2个S波层析模型计算的核幔边界起伏 Fig. 3 CMB topography computed using two S-wave tomography models |
从图 3可以看出,2个S波层析模型对应的核幔边界起伏幅度约为-5~5 km。正值表示核幔边界的隆起,负值表示凹陷。核幔边界的2个明显的大尺度隆起位于太平洋区域和非洲南部下方,核幔边界的凹陷则主要围绕这2个隆起区域分布。这2个明显的大尺度隆起可能对应核幔边界附近的2个超级低速异常带[24-25],是超级地幔柱的起源。
图 3还显示,下地幔与上地幔的粘度比值分别为40、50、60、70时,每个层析模型对应的核幔边界起伏形态及幅值差异不大,预示着核幔边界起伏对下地幔的粘度变化不敏感。另外,不同层析模型得到的核幔边界起伏形态大致相同,在太平洋区域的正异常及全球范围内的负异常的形态显示了较小的差异,这些差异可能由不同的层析模型本身的差异引起。
3 分析核幔边界起伏的研究仍然是地学界的热点问题。由于全球地震数据的不均匀分布、数据处理方法以及对核幔边界起伏的计算方法的不同,目前核幔边界起伏的研究还存在很多不确定性。为分析2个层析模型得到的结果的可靠性,对2个模型计算的核幔边界起伏作差,并对结果进行分析。另外,将本文结果与已有结果进行比较,对瞬时地幔对流问题求解过程中可能存在的不足进行分析。最后,分析核幔边界上部D″层对核幔边界起伏的可能影响。
3.1 2个层析模型计算的核幔边界起伏之差对2个层析模型计算的核幔边界起伏进行作差,得到的残差如图 4所示。

|
图 4 2个层析模型对应的核幔边界起伏的差值 Fig. 4 Difference of CMB topography computed from two tomography models |
图 4显示,2个层析模型得到的核幔边界起伏的差值在全球范围内的分布与核幔边界起伏形态不存在明显的相似性,但是残差的幅值达到-2.5~3.5 km的范围。上述表明,由2个层析模型计算的核幔边界起伏在全球范围内分布符合较好,但是核幔边界起伏的幅度还存在很大不确定性。
3.2 本文结果与已有研究结果的对比本文用2个层析模型得到的核幔边界起伏幅度约为-5~5 km,与Yoshida运用数值模拟方法得到的核幔边界起伏相比,幅值及分布都比较符合,结果对照如图 5。

|
图 5 本文计算的核幔边界起伏与Yoshida结果的对比 Fig. 5 Comparing the CMB topography in this study with that from Yoshida |
图 5显示,本文计算的核幔边界起伏与Yoshida用数值法计算的结果在分布形态上存在一定的差异,这主要源于本文和Yoshida在数值模拟时采用的层析模型及粘度结构的差异。Yoshida采用的层析模型是Smean,本文中使用的2个模型分别为SEMUCB_WM1和S40RTS。
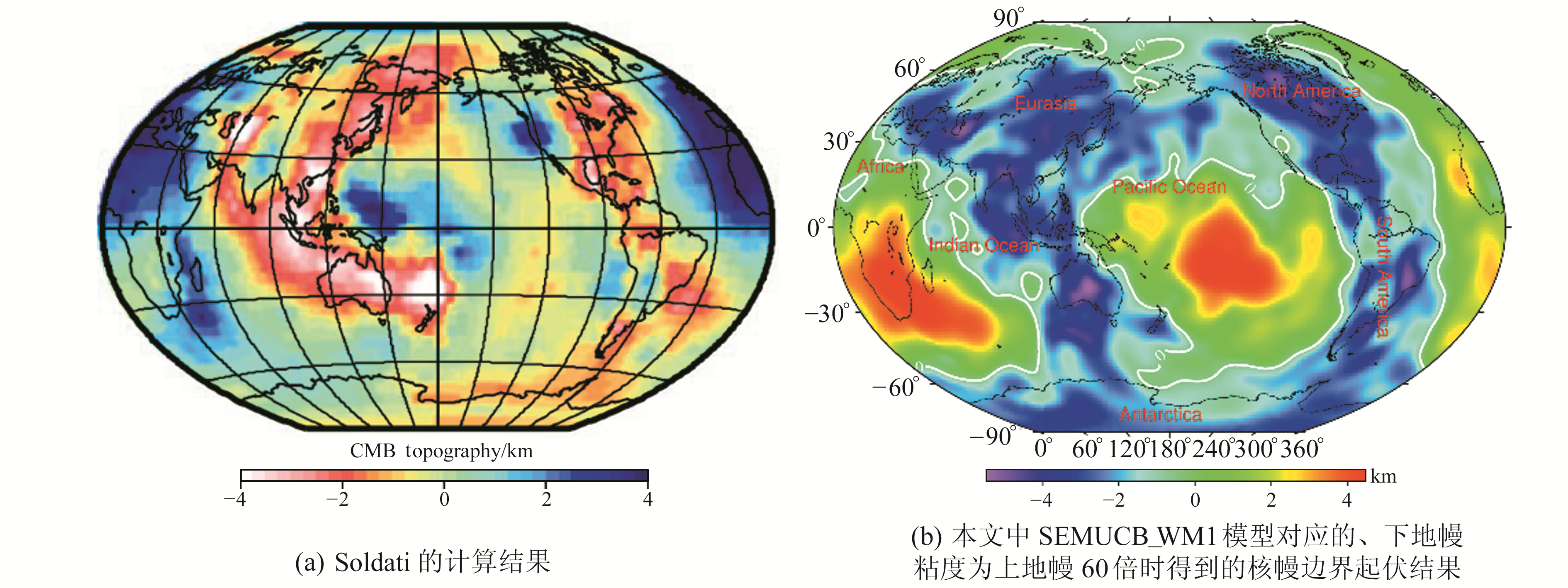
将本文结果与Soldati等[26]运用经典的地震波走时差反演得到的核幔边界起伏进行对比,结果如图 6所示。图中显示,本文结果与Soldati等得到的结果在幅值及分布上大致吻合;在太平洋区域的分布形态存在一定的差异,这种差异可能主要源于使用的计算方法和数据类型不同造成的结果误差。
|
图 6 本文计算的核幔边界起伏与Soldati等结果的对比 Fig. 6 Comparing the CMB topography in this study with that from Soldati |
本文得到的核幔边界起伏的幅度约为-5~5 km,与Gwinn等[27]用VLBI方法得到的核幔边界扁率结果(490±110 m)相比幅值较大。有学者认为,下地幔底部、核幔边界上方的D″层的存在可能会削弱地幔对流在核幔边界产生的动力学地形,但还没有得到确定的结论。Lassak等[28]用数值法模拟地幔对流引起的核幔边界起伏形态,探索核幔边界上部热化学堆积及地幔羽群对核幔边界起伏的影响,认为热化学堆积会产生中部较平坦的核幔边界地形隆升,地幔羽群使上涌流下方产生不太集中分布的向上挠曲。但核幔边界附近D″层对核幔边界起伏幅值影响的研究有待进一步确认。
4 结语本文利用数值法求解瞬时地幔对流问题,用2个较新的S波速度异常模型转换为密度异常作为驱动瞬态地幔热对流的浮力项,模拟得到核幔边界起伏幅值约为-5~5 km。本文结果与Yoshida利用数值模拟方法得到的结果及Soldati等利用经典的地震波走时差反演得到的核幔边界起伏结果相比,幅值与两者均比较符合;在分布形态上,本文模拟结果与Yoshida的结果比较一致,与Soldati等得到的结果大体符合,局部特征存在一定的差异。
本文在进行数值模拟地幔对流时,为便于计算作了一些假设,如文中假定地幔对流仅为热对流,没有考虑热化学对流的情形。另外,本文也没有考虑地幔底部D″层对核幔边界起伏可能存在的影响。以上这些复杂因素对数值模拟核幔边界起伏的影响可在今后的研究中进行深入探讨。
| [1] |
Morelli A, Dziewonski A M. Topography of the Core-Mantle Boundary and Lateral Homogeneity of the Liquid Core[J]. Nature, 1987, 325(6 106): 678-683
(  0) 0) |
| [2] |
Yoshida M. Core-Mantle Boundary Topography Estimated from Numerical Simulations of Instantaneous Mantle Flow[J]. Geochemistry, Geophysics, Geosystems, 2008, 9(7)
(  0) 0) |
| [3] |
Zhong S J, McNamara A, Tan E, et al. A Benchmark Study on Mantle Convection in a 3-D Spherical Shell Using CitcomS[J]. Geochemistry, Geophysics, Geosystems, 2008, 9(10)
(  0) 0) |
| [4] |
Zhong S J, Zuber M T, Moresi L, et al. Role of Temperature-Dependent Viscosity and Surface Plates in Spherical Shell Models of Mantle Convection[J]. Journal of Geophysical Research, 2000, 105(B5): 11 063-11 082 DOI:10.1029/2000JB900003
(  0) 0) |
| [5] |
Yoshida M, Nakakuki T. Effects on the Long-Wavelength Geoid Anomaly of Lateral Viscosity Variations Caused by Stiff Subducting Slabs, Weak Plate Margins and Lower Mantle Rheology[J]. Physics of the Earth and Planetary Interiors, 2009, 172(3-4): 278-288 DOI:10.1016/j.pepi.2008.10.018
(  0) 0) |
| [6] |
Zhong S J, Davies G F. Effects of Plate and Slab Viscosities on the Geoid[J]. Earth and Planetary Science Letters, 1999, 170(4): 487-496 DOI:10.1016/S0012-821X(99)00124-7
(  0) 0) |
| [7] |
Moresi L, Gumis M. Constraints on the Lateral Strength of Slabs from Three-Dimensional Dynamic Flow Models[J]. Earth and Planetary Science Letters, 1996, 138(1-4): 15-28 DOI:10.1016/0012-821X(95)00221-W
(  0) 0) |
| [8] |
French S W, Romanowicz B A. Whole-Mantle Radially Anisotropic Shear Velocity Structure from Spectral-Element Waveform Tomography[J]. Geophysical Journal International, 2014, 199(3): 1 303-1 327 DOI:10.1093/gji/ggu334
(  0) 0) |
| [9] |
Ritsema J, Deuss A, Heijst H J V, et al. S40RTS: A Degree-40 Shear-Velocity Model for the Mantle from New Rayleigh Wave Dispersion, Teleseismic Traveltime and Normal-Mode Splitting Functions Measurements[J]. Geophysical Journal International, 2011, 184(3): 1 223-1 236 DOI:10.1111/j.1365-246X.2010.04884.x
(  0) 0) |
| [10] |
Liu X, Zhong S J. Constraining Mantle Viscosity Structure for a Thermochemical Mantle Using the Geoid Observation[J]. Geochemistry, Geophysics, Geosystems, 2016, 17(3): 895-913 DOI:10.1002/2015GC006161
(  0) 0) |
| [11] |
Ghosh A, Becker T W, Humphreys E D. Dynamics of the North American Continent[J]. Geophysical Journal International, 2013, 194(2): 651-669 DOI:10.1093/gji/ggt151
(  0) 0) |
| [12] |
Ghosh A, Thyagarajulu G, Steinberger B. The Importance of Upper Mantle Heterogeneity in Generating the Indian Ocean Geoid Low[J]. Geophysical Research Letters, 2017, 44(19): 9 707-9 715 DOI:10.1002/2017GL075392
(  0) 0) |
| [13] |
Spasojevic S, Gurnis M, Sutherland R. Mantle Upwellings above Slab Graveyards Linked to the Global Geoid Lows[J]. Nature Geoscience, 2010, 3(6): 435-438 DOI:10.1038/ngeo855
(  0) 0) |
| [14] |
Becker T W. On the Effect of Temperature and Strain-Rate Dependent Viscosity on Global Mantle Flow, Net Ratation, and Plate-Driving Forces[J]. Geophysical Journal International, 2006, 167(2): 943-957 DOI:10.1111/j.1365-246X.2006.03172.x
(  0) 0) |
| [15] |
Haskell N A. The Motion of a Viscous Fluid Under a Surface Load[J]. Physics, 1935, 6(8): 265-269
(  0) 0) |
| [16] |
Yang T, Gurnis M. Dynamic Topography, Gravity and the Role of Lateral Viscosity Variations from Inversion of Global Mantle Flow[J]. Geophysical Journal International, 2016, 207(2): 1 186-1 202 DOI:10.1093/gji/ggw335
(  0) 0) |
| [17] |
Karato S. Deformation of Earth Materials: An Introduction to the Rheology of Solid Earth[M]. Cambridge: Cambridge University Press, 2008
(  0) 0) |
| [18] |
King S D. Mantle Downwellings and the Fate of Subducting Slabs: Constraints from Seismology, Geoid Topography, Geochemistry, and Petrology[M]. New York: Elsevier, 2007
(  0) 0) |
| [19] |
Ghosh A, Becker T W, Zhong S J. Effects of Lateral Viscosity Variations on the Geoid[J]. Geophysical Research Letters, 2010, 37(1)
(  0) 0) |
| [20] |
Zhong S J, Zuber M T, Moresi L, et al. Role of Temperature-Dependent Viscosity and Surface Plates in Spherical Shell Models of Mantle Convection[J]. Journal of Geophysical Research, 2000, 105(B5): 11 063-11 082 DOI:10.1029/2000JB900003
(  0) 0) |
| [21] |
Moresi L, Solomatov V. Mantle Convection with a Brittle Lithosphere Thoughts on the Global Tectonic Styles of the Earth and Venus[J]. Geophysical Journal International, 1998, 133(3): 669-682 DOI:10.1046/j.1365-246X.1998.00521.x
(  0) 0) |
| [22] |
Liu X, Zhong S J. The Long-Wavelength Geoid from Three-Dimensional Spherical Models of Thermal and Thermochemical Mantle Convection[J]. Journal of Geophysical Research: Solid Earth, 2015, 120(6): 4 572-4 596 DOI:10.1002/2015JB012016
(  0) 0) |
| [23] |
Tan E, Choi E, Thoutireddy P, et al. GeoFramework: Coupling Multiple Models of Mantle Convection within a Computational Framework[J]. Geochemistry, Geophysics, Geosystems, 2006, 7(6)
(  0) 0) |
| [24] |
Halldórsson S A, Hilton D R, Scarsi P, et al. A Common Mantle Plume Source beneath the Entire East African Rift System Revealed by Coupled Helium-Neon Systematics[J]. Geophysical Research Letters, 2014, 41(7): 2 304-2 311 DOI:10.1002/2014GL059424
(  0) 0) |
| [25] |
Schmerr N, Garnero E, McNamara A. Deep Mantle Plumes and Convective Upwelling beneath the Pacific Ocean[J]. Earth and Planetary Science Letters, 2010, 294(1-2): 143-151 DOI:10.1016/j.epsl.2010.03.014
(  0) 0) |
| [26] |
Soldati G, Koelemeijer P, Boschi L, et al. Constraints on Core-Mantle Boundary Topography from Normal Mode splitting[J]. Geochemistry, Geophysics, Geosystems, 2013, 14(5): 1 333-1 342 DOI:10.1002/ggge.20115
(  0) 0) |
| [27] |
Gwinn C R, Herring T A, Shapiro L L. Geodesy by Radio Interferometry: Studies of the Forced Nutations of the Earth: 2. Interpretation[J]. Journal of Geophysical Research, 1986, 91(B5): 4 755-4 765 DOI:10.1029/JB091iB05p04755
(  0) 0) |
| [28] |
Lassak T M, McNamara A K, Garnero E J, et al. Core-Mantle Boundary Topography as a Possible Constraint on Lower Mantle Chemistry and Dynamics[J]. Earth and Planetary Science Letters, 2010, 289(1-2): 232-241 DOI:10.1016/j.epsl.2009.11.012
(  0) 0) |
2. The First Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China
 2020, Vol. 40
2020, Vol. 40

