2. 武汉大学测绘学院,武汉市珞喻路129号,430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
监测陆地沉降的传统方法有水准监测、全球定位系统(GNSS)观测等。水准测量精度较高,但劳动强度大和费时[1],且测量误差会随着水准路线的延长而累积,因此不适用于大面积的沉降监测。GNSS广泛用于陆地沉降监测,能迅速获得cm级精度的三维坐标[2],考虑到成本因素,GNSS技术不适用于监测点密集分布的情况。干涉合成孔径雷达(InSAR)是另一种广泛用于监测地面沉降的替代技术[3],但InSAR测量的时间跨度很短,无法分析地面沉降的长期变化。由于上述技术均有各自的优缺点和局限性,本文提出利用卫星测高监测地面沉降的方法,可作为传统监测手段的有效补充。
从20世纪80年代发展至今,卫星测高技术精度取得了较大提高,对海洋测量精度达到cm级。最早用于地面沉降监测是结合验潮站数据和测高数据计算验潮站的沉降,另外有学者用T/P测高数据研究地面沉降[4-5]。地下水与地面沉降存在紧密的联系,地下水水位持续下降会产生大面积的地下水降落漏斗,从而导致地面沉降和土壤盐碱化等一系列地质环境问题。目前,测井是地下水水位监测的最常用方法,但依靠单点的地下水位,难以反映地下水储量(GWS)的时空变化特征;水文模型可用于估计地下水储量变化,但在模型刻画及数据获取方面存在很大的局限性。卫星重力技术(GRACE)作为一种新的陆地水储量监测手段,打破了传统地面观测在时空上的局限性,已在国内外水储量变化研究中得到了应用[6-8], 且监测效果较好。
本文首次在华北和上海地区尝试利用测高技术监测地面沉降,结果表明,测高技术可以作为传统地面沉降监测的补充手段,尤其对于GNSS和水准网络未覆盖区域的沉降监测具有重要意义。同时,本文结合GRACE和水文模型数据探讨了地面沉降与地下水变化的关系。
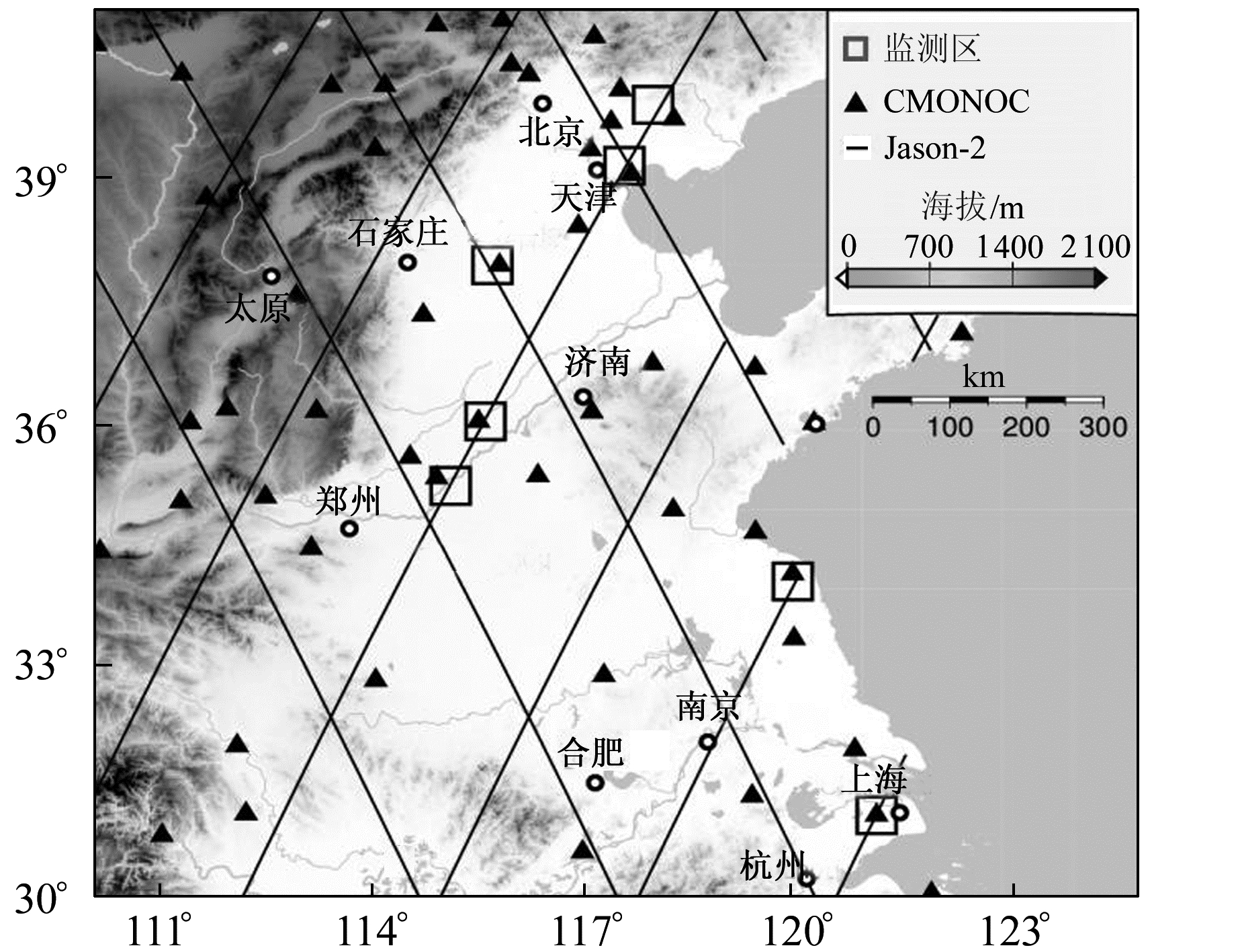
1 研究区域及实验数据华北和上海地区是我国经济发达、人口密集的地区,在长时间的地下水抽取以及大规模城市建设等因素共同作用下,该区域的地面沉降日益剧烈,需要持续监测地面沉降情况。本文选取附近有测高轨迹经过的GNSS站点周边作为研究区域,研究区域的简要情况说明见图 1和表 1。本研究利用Jason-2卫星传感器地球物理数据记录(SGDR)观测地面沉降,采用高分辨率的数字地形模型(SRTM)进行地形改正。最后,利用陆态网(CMONOC)数据检核测高数据计算的地面沉降速率。利用GRACE RL05数据反演区域陆地水储量变化,移去水文模型(GLDAS)获取的土壤水变化,得到地下水储量变化,进而分析研究区域地面沉降原因的差异。
|
图 1 研究区域分布 Fig. 1 Distribution of the study areas |
|
|
表 1 研究区域概况 Tab. 1 Overview of the study areas |
利用卫星测高确定地表高程的方法与确定海水面高的方法相同。根据卫星测高原理可知,地表高程计算公式为:
| $ \mathrm{LSH}=\mathrm{Alt}-\text { Range }_{-} \mathrm{ku}-\text { Corr } $ | (1) |
式中,LSH为地表高程,Alt为卫星的椭球高,Range_ku为Ku波段雷达测高计测定的卫星与地面间距离。Corr为误差改正项,具体的误差改正为:
| $ {\rm{Corr = Dry + Wet + Iono + Earth + Pole}} $ | (2) |
式中,Dry为干对流层延迟改正,Wet为湿对流层延迟改正,Iono为电离层改正,Earth为固体潮改正,Pole为极潮改正。以上各改正项可从SGDR数据文件中读取。
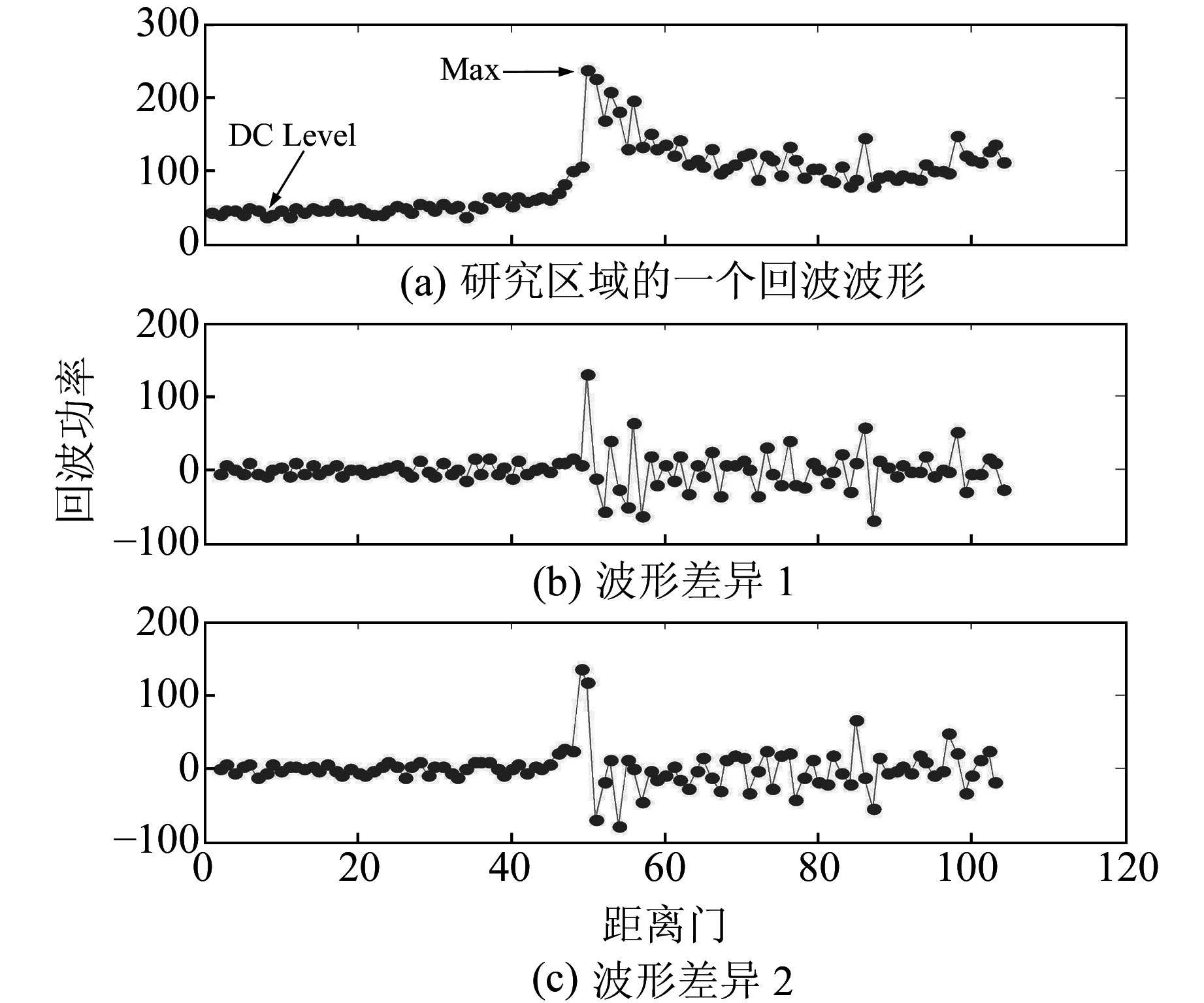
2.2 改进阈值法由于陆地区域测高计返回波形较复杂且与Brown模型差异很大,致使陆地测高数据精度远低于海洋区域。因此,运用卫星测高监测地面沉降的关键在于选取合适的波形重跟踪方法[9]。本文采用阈值法和改进阈值法进行比较。对于复杂波形而言,简单的阈值法不能准确地确定波形前缘中点。首先,阈值法仅用前几个采样点的均值作为计算热噪声的标准,而陆地回波前段采样点的起伏会导致热噪声错估;其次,海洋波形的最大功率一般在前缘处,而陆地波形的最大功率存在不确定性。改进阈值法[4]通过计算2种波形差异(记为Diff1和Diff2)来确定回波的热噪声和最大功率(图 2):
| $ {\rm{Diff }}1(i) = P(i + 1) - P(i) $ | (3) |
| $ {{\rm{Diff }}2(i) = P(i + 2) - P(i)} $ | (4) |
|
图 2 改进阈值法确定波形前缘中点 Fig. 2 The leading edge midpoint of waveform determined by the modified threshold retracker |
式中,P(i)是第i个距离门的回波功率,Jason-2卫星中i=1~104。
回波的热噪声和最大功率可以通过3个步骤来确定:
1) 从Diff1中搜索第1个由正变负的值,即为波形的热噪声水平,位置记为第i个采样;
2) 从Diff2的第i个采样点开始搜索第1个由正变负的值,位置记为第n个采样点,如果Diff1(n)也为负值,则第n个采样点对应的值为回波的最大功率;否则,第n+1个采样点对应的值为回波的最大功率;
3) 用参数为10%的传统阈值法计算波形前缘中点的位置,根据波形实际前缘中点与星载跟踪点位置差值以及光速,可以计算出重跟踪改正ΔR:
| $ \Delta R = \left( {{N_{{\rm{ret}}}} - {N_{{\rm{tr}}}}} \right) \times {G_{2m}} $ | (5) |
式中,Nret为波形重跟踪计算的前缘中点位置;Ntr为星载跟踪点位置;G2m为与雷达高度计脉冲宽度有关的距离转换因子,可以根据脉冲宽度tw和光速(c=299 792 458 m/s)计算,公式为:G2m=tw·c/2。
利用卫星测高确定地面高程时,由于反射面的坡度,反射点从星下点向上坡偏移,造成卫星到星下点的距离与到反射点的距离之间存在差别,即坡度误差。坡度较大的地区必须进行坡度误差改正,本文采用重定位法[10]进行坡度改正。重定位法是将坡度误差看作是距离误差和位置误差的合成,即首先估计与距离观测值相应的近距离的位置,然后以近距离点作为新的星下点,计算其到卫星轨道的距离,从而得到距离改正值:
| $ H_{c}=R_{s}\left(1-\frac{\sin (\alpha-\theta)}{\sin a}\right) $ | (6) |
式中,Hc为地形坡度改正后的距离观测值,Rs为测高卫星的地心距,α为地形坡度。改正前后2个位置所对应的球心角为
Jason-2卫星星下点实际地面轨迹与设计轨迹并不重合,为了将实际轨迹校正为设计轨迹,采用前面提到的SRTM模型的双线性内插数据进行地形梯度改正[10]:
| $ \mathrm{LSH}_{\text {corr }}=\mathrm{LSH}_{\text {ori }}+\left(\mathrm{DEM}_{\text {corr }}-\mathrm{DEM}_{\text {ori }}\right) $ | (7) |
式中,LSHcorr为地形梯度改正后的地面高,LSHori为地形梯度改正前的地面高(即测高观测值),DEMcorr为正常轨迹的数字地形高程,DEMori为实际轨迹的数字地形高程。
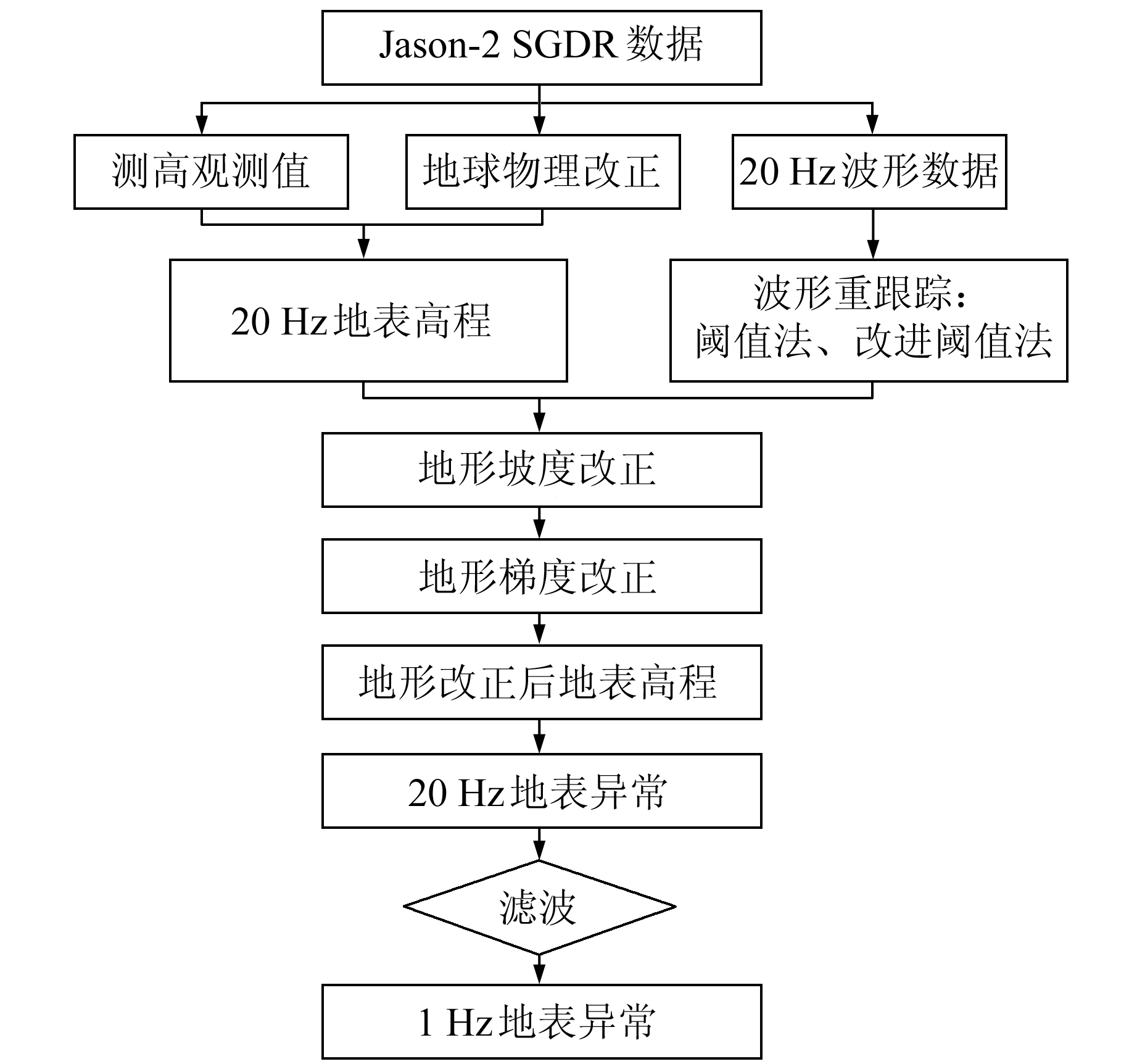
然后,从改正后的LSH中减去相应的DEM值得到地表异常,在20 Hz地表异常数据中用滤波方法消去噪声。从Jason-2地表异常中移去粗差点之后,用简单的移动平均方法得到1 Hz地面异常,再用矩形滤波器进行空间平滑,详细测高数据处理流程见图 3。最后,用每个研究区域计算得到的1 Hz地面异常数据计算沉降速率,并与GNSS观测数据进行比较。
|
图 3 利用测高技术监测地表沉降的数据处理流程 Fig. 3 Flowchart of monitoring land surface subsidence by Jason-2 satellite altimeter |
依据处理流程图得到的各研究区域地表异常时间序列如图 4所示,各时间序列的振幅为0.5~1.0 m,其中,由于TJNH、SHAO、HBSZ研究区域内测高卫星星下点轨迹通过雷达散射条件较复杂的城市和多植被覆盖的地区,以上3处区域数据处理得到的时间序列抖动比较剧烈。用线性回归方法计算出各研究区域的地面沉降趋势(见表 2,单位mm/a),由表 2可见,经阈值法和改进阈值法波形重跟踪改正后,各研究区域地面沉降趋势标准差的均值分别减小0.12 mm/a和0.18 mm/a,说明重跟踪技术可有效提高地面沉降速率的计算精度。

|
图 4 卫星测高监测陆地沉降时间序列 Fig. 4 The time series of land subsidence monitoring by satellite altimetry |
|
|
表 2 研究区域中卫星测高观测值计算地面沉降速率 Tab. 2 The subsidence rate calculated from satellite altimetry in the study areas |
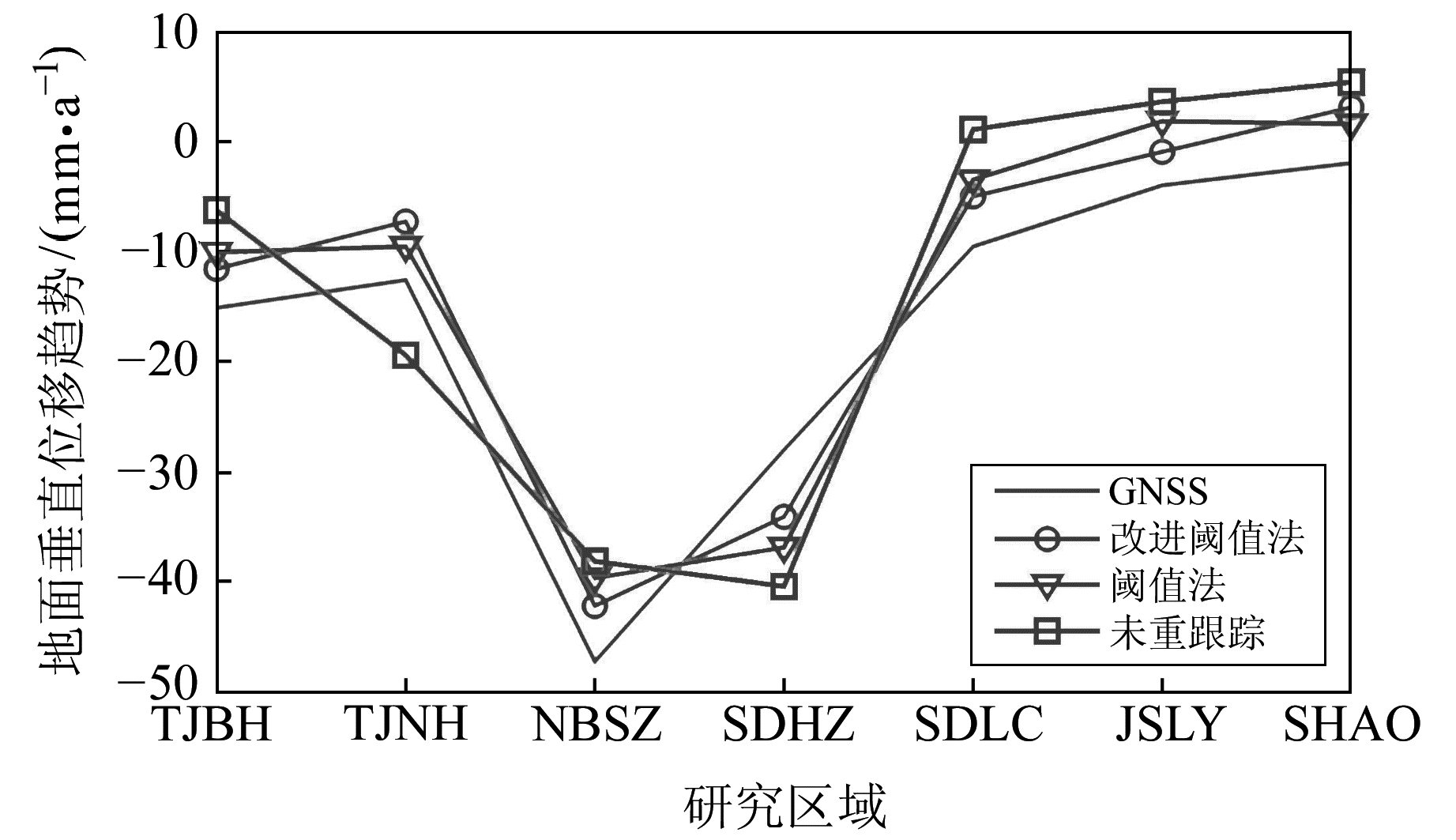
文中选用研究区域测高卫星轨迹附近的GNSS基准站垂直位移时间序列作为独立观测数据,检验卫星测高数据计算地面沉降趋势的精度。由图 5和表 3可见,利用未进行重跟踪改正的测高数据计算得到的地面沉降年速率的平均偏差为-3.4 mm/a、标准差为9.1 mm/a,与各研究区域的GNSS基准站数据计算的沉降趋势时间序列相比,相关系数为0.88。经阈值法和改进阈值法进行重跟踪改正后,沉降速率的平均偏差分别提高到-3.2 mm/a和-2.9 mm/a,标准差分别为5.5 mm/a和4.1 mm/a(标准差分别减小40%和55%),相关系数分别达到0.94和0.97。
|
图 5 卫星测高与GNSS观测值计算地面沉降对比 Fig. 5 Comparisons of land subsidence calculated by altimetry and GNSS observations |
|
|
表 3 测高监测地面沉降趋势精度统计 Tab. 3 Statistics of land subsidence rate accuracy derived by altimetry |
根据Wahr方法[11]推导由GRACE时变重力资料解算的陆地水储量如下:
| $ \begin{array}{*{20}{c}} {{\rm{TWS}}(\theta , \lambda ) = \frac{{a{\rho _{{\rm{ave }}}}}}{{3{\rho _{{\rm{water }}}}}}\sum\limits_{l = 0}^\infty {\sum\limits_{m = 0}^l {{{\bar P}_{lm}}} } \frac{{2l + 1}}{{1 + {k_l}}} \cdot }\\ {\left( {\Delta {C_{lm}}\cos (m\lambda ) + \Delta {S_{lm}}\sin (m\lambda )} \right)} \end{array} $ | (8) |
式中,a为地球半径,ρave为地球平均密度(5 517 kg/m3),ρwater为水的密度(1 000 kg/m3),
区域水储量变化的基本平衡方程为:
| $ \Delta \mathrm{GWS}=\Delta \mathrm{TWS}-\Delta \mathrm{SM}-\Delta \mathrm{SWE} $ | (9) |
式中,ΔGWS为地下水变化,ΔTWS、ΔSM、ΔSWE分别表示GRACE卫星反演得到的陆地水变化、土壤水变化、冰雪变化。由于地表水和植被水变化较小,在本文研究中不考虑这两项因素。
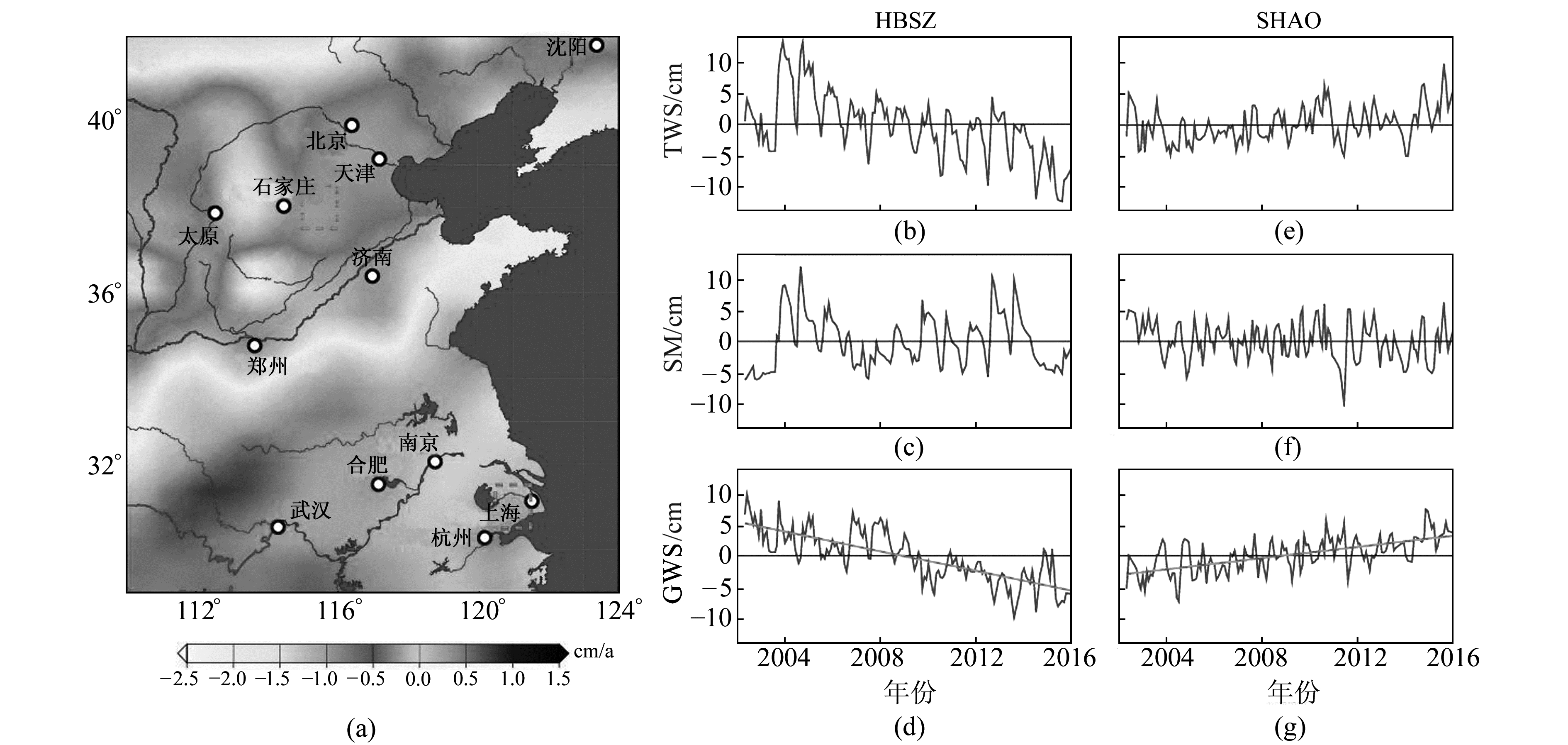
从GRACE反演的陆地水储量变化中扣除由GLDAS估算的土壤水和冰雪变化得到区域地下水储量变化,图 6为通过去相关滤波P3M6与300 km高斯滤波的组合方法反演GRACE等效水高,扣除GLDAS_Noah水文模型的土壤、植被和雪水等变化,得到2002~2015年中国东部地区地下水储量变化趋势。图 6显示,中国北部(尤其是黄河流域)地下水储量整体呈减少的趋势,南方则出现地下水上升的情况。GRACE获取的地下水变化与测高观测的区域地面平均沉降结果一致,说明地面沉降与地下水变化具有较好的一致性。
|
图 6 利用GRACE-GLDAS模型获取的地下水等效水高变化 Fig. 6 The equivalent water height change of groundwater obtained by GRACE-GLDAS model |
在华北及上海选取部分区域作为研究对象,利用卫星测高数据计算地面沉降趋势,与GNSS观测结果一致性较高。其中,经过改进阈值法校正的计算结果最优,不确定度为4.1 mm/a,相关性达到0.97。实验结果表明,卫星测高可用于陆地地面沉降的研究,尤其对于偏远地区的地面沉降监测具有重要意义。目前,卫星测高计划可以提供长达27 a的连续观测数据,随着后续测高卫星任务的延续,观测时间还可以进一步延长,为该项研究提供了可靠的数据保证。由于受卫星轨道分布的限制,测高技术只能监测卫星轨迹通过的有限区域,并且在现有雷达测高计精度条件下,无法实现卫星测高对复杂地形区域的地面沉降监测。为实现大面积及复杂地形区域的地面沉降监测,需提高测高数据精度和优化数据处理方案。
致谢: 感谢CNES提供研究所需的Jason-2卫星SGDR数据,感谢中国地震局提供CMONOC时间序列,感谢NASA提供GRACE RL05数据以及GLDAS_Noah模型。
| [1] |
塔拉, 陈阜超, 韩月萍. 利用水准资料研究天津地区沉降动态特征[J]. 大地测量与地球动力学, 2013, 33(5): 11-15 (Ta La, Chen Fuchao, Han Yueping. Research on Dynamic Characteristics of Land Subsidence in Tianjin Using Leveling Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(5): 11-15)
(  0) 0) |
| [2] |
吴继忠, 朱丽强, 龚俊. 利用连续GPS观测数据分析长江三角洲地区地壳变形[J]. 武汉大学学报:信息科学版, 2015, 40(10): 1 324-1 328 (Wu Jizhong, Zhu Liqiang, Gong Jun. An Analysis of the Crustal Deformation in the Yangtze River Delta Area Using Continuous GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1 324-1 328)
(  0) 0) |
| [3] |
Hung W, Hwang C, Chen Y, et al. Surface Deformation from Persistent Scatters SAR Interferometry and Fusion with Leveling Data: A Case Study over the Choushui River Alluvial Fan, Taiwan[J]. Remote Sensing of Environment, 2011, 115(4): 957-967 DOI:10.1016/j.rse.2010.11.007
(  0) 0) |
| [4] |
Lee H, Shum C K, Yi Y C, et al. Laurentia Crustal Motion Observed using TOPEX/POSEIDON Radar Altimetry over Land[J]. Journal of Geodynamics, 2008, 46(3-5): 182-193 DOI:10.1016/j.jog.2008.05.001
(  0) 0) |
| [5] |
Kuo C, Cheng Y, Lan W, et al. Monitoring Vertical Land Motions in Southwestern Taiwan with Retracked Topex/ Poseidon and Jason-2 Satellite Altimetry[J]. Remote Sensing, 2015, 7(4): 3 808-3 825 DOI:10.3390/rs70403808
(  0) 0) |
| [6] |
Rodell M, Velicogna I, Famiglietti J S. Satellite-Based Estimates of Groundwater Depletion in India[J]. Nature, 2009, 460(7 258): 999-1 002
(  0) 0) |
| [7] |
罗志才, 李琼, 钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676-681 (Luo Zhicai, Li Qiong, Zhong Bo. Water Storage Variations in Heihe River Basin Recovered from GRACE Temporal Gravity Filed[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 676-681)
(  0) 0) |
| [8] |
Feng W, Zhong M, Lemoine J M, et al. Evaluation of Groundwater Depletion in North China Using the Gravity Recovery and Climate Experiment(GRACE) Data and Ground-Based Measurements[J]. Water Resources Research, 2013, 49(4): 2 110-2 118 DOI:10.1002/wrcr.20192
(  0) 0) |
| [9] |
Huang Z K, Wang H H, Luo Z C, et al. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms[J]. Remote Sensing, 2017, 9(10): 1 077 DOI:10.3390/rs9101077
(  0) 0) |
| [10] |
汪海洪, 刘玉春, 王文波. 卫星雷达测高数据的坡度改正方法比较[J]. 大地测量与地球动力学, 2013, 33(6): 68-71 (Wang Haihong, Liu Yuchun, Wang Wenbo. Comparison on Slope Correction Methods for Satellite Radar Altimetry Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 68-71)
(  0) 0) |
| [11] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30 205-30 229 DOI:10.1029/98JB02844
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2020, Vol. 40
2020, Vol. 40

