近年来,室内定位已逐渐成为众多终端应用中的一项基础功能,在军事、民用、灾害防护及维和任务等方面均有应用[1]。相比于室外较为单一地依赖卫星定位,室内场景可用于定位的信号源众多,国内部分学者[2-4]对室内定位源进行了研究。不同的室内定位信号源也产生了多种室内定位算法:基于测距的定位算法,该算法所依赖的硬件具有直接测距能力,如UWB;基于无线信号强度的定位算法,其中典型的称为指纹定位,这种方法通常用于精度要求很低的场景;基于行人航迹推算(pedestrian dead reckoning,PDR)的定位方法等。
在众多室内定位解决方案中,UWB定位方法因其高带宽、高分辨率、高传输速率、强鲁棒性、低功耗以及成本低等优势,已成为室内定位中最有前景的解决方案之一。主流的UWB定位算法包括基于TOF的[5]、基于到达时间差(time difference of arrival,TDOA)的[6]、基于到达角度(angel of arrival,AOA)的和基于接收信号强度(received signal strengths,RSS)的定位算法[7],后2种方法因适用场景少、易受干扰和定位精度差等原因较少被采用。影响UWB定位精度的一个重要因素为非视距(non-line of sight,NLOS)环境,在NLOS场景下,UWB/TOF测距精度会显著变差[8]。此外与卫星定位相似,复杂的室内环境容易引起多径效应,对室内定位的精度也有很大影响,因此必须对TOF测距加以修正。本文阐述了TOF测距原理,利用卡尔曼滤波及其变式对原始TOF测距值进行处理,剔除TOF测距粗差,降低TOF测距噪声以及减弱NLOS环境对TOF测距的影响,利用已知距离测量值标定TOF测距,从而精确改正TOF测距系统误差。同时在UWB静态与动态定位中,利用卡尔曼滤波实时估计目标位置与速度,从而平滑目标运动轨迹。
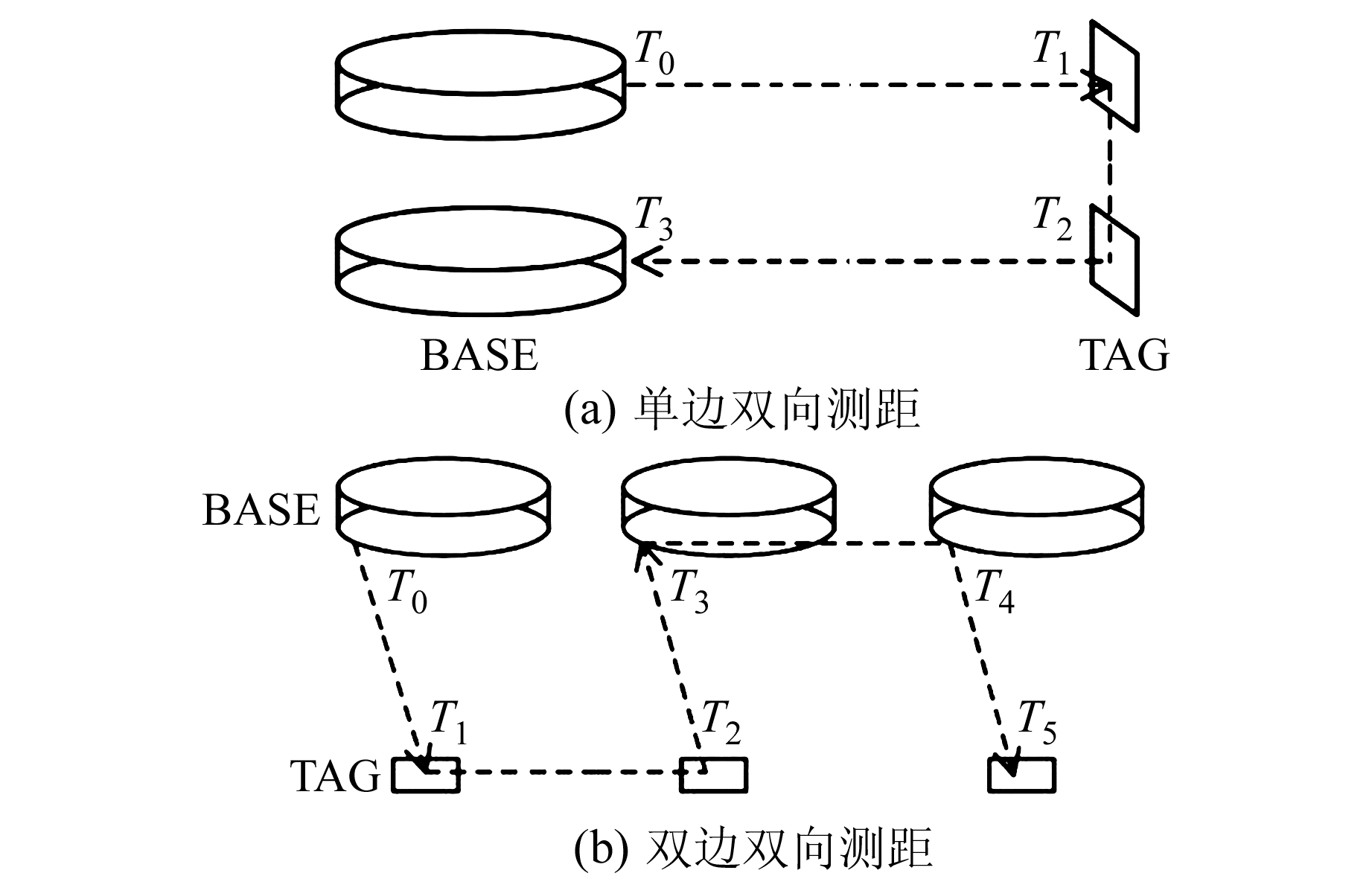
1 UWB/TOF测距原理本文实验采用的基站与标签均为Decawave公司生产的DW1000设备。该设备提供UWB信号的发收、时间戳记录与延时发送等功能, 在硬件间时钟不同步的前提下,可采用单边双向测距(single-sided two-way ranging,SS-TWR),其原理见图 1(a)。飞行时间计算公式为:
| $ \mathrm{TOF}=\frac{1}{2} \times\left(\left(T_{3}-T_{0}\right)-\left(T_{2}-T_{1}\right)\right) $ | (1) |
|
图 1 两种TOF测距模式 Fig. 1 Two TOF measuring modes |
该方法并不常用,原因是基站与标签的时钟与标准时钟相比存在偏差,用时钟漂移率k来表示,取k=10 ppm。假设标签延时时间Td为3 ms,飞行时间TOF与延时时间相比可忽略不计,则由延时时间Td带来的测距误差为:
| $ |r|=\frac{1}{2} \times\left|k_{b}-k_{t}\right| \times T_{d} \times c $ | (2) |
当|kb-kt|=5 ppm,|r|≈2.25 m,实际情况下|kb-kt|可能比5 ppm更高,会带来很大的测距误差。为了减小时钟漂移对测距的影响,采用双边双向测距(double-sided two-way ranging,DS-TWR)法,该方法在SS-TWR基础上再增加一次延时和UWB信号的发收(图 1(b))。DS-TWR法的TOF计算方法为:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{r1}} = {T_3} - {T_0} \cdot {T_{p1}} = {T_2} - {T_1}}\\ {{T_{r2}} = {T_5} - {T_2}, {T_{p2}} = {T_1} - {T_3}}\\ {{\mathop{\rm TOF}\nolimits} = \frac{{{T_1} \times {T_2} - {T_{p1}} \times {T_{p2}}}}{{{T_{r1}} + {T_{r2}} + {T_{p1}} + {T_{p2}}}}} \end{array}} \right. $ | (3) |
该方法因钟漂而带来的测距误差近似计算公式为:
| $ |r| \approx \operatorname{TOF} \times \frac{\left|k_{b}+k_{t}\right|}{2} \times c $ | (4) |
取kb和kt均为20 ppm,若基站与标签距离为200 m,TOF约为666 ns,测距误差为:
| $ |r|=666 \times 10^{-9} \times 20 \times 10^{-6} \times \\ 3 \times 10^{8} \approx 0.004 \mathrm{m} $ |
即DS-TWR法因时钟漂移带来的测距误差为mm级,因此实际TOF工作模式应采用DS-TWR法。
图 2对比了2种测距法的测距效果,可以看出,DS-TWR法相较于SS-TWR法,抗钟漂效果提升明显,测距值稳定性更强。

|
图 2 单边双向测距与双边双向测距比较 Fig. 2 Comparison between SS-TWR and DS-TWR |
理想室内环境下的UWB测距值同样存在粗差与噪声,为了剔除粗差、降低噪声水平,用TOF距离值和距离变化率作为系统状态向量Xk,建立TOF距离模型:
| $ \boldsymbol{X}_{k}={\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \boldsymbol{X}_{k-1}+\boldsymbol{w}_{k} $ | (5) |
系统观测方程为:
| $ {\mathit{\boldsymbol{Z}}_k} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{v}}_k} $ | (6) |
为了剔除TOF粗差,在标准卡尔曼滤波过程中,对于增益矩阵
| $ \boldsymbol{K}_{k}=\boldsymbol{P}_{k, k-1} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k, k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} $ | (7) |
当k时刻观测噪声Rk增大,Kk会相应减小,新观测值对系统状态和状态协方差矩阵的影响也相应减小,为此一个可行的粗差剔除思路为[9]:
1) 一步预测Xk, k-1,Pk, k-1,并计算一步预测残差值rk= Zk- HXk, k-1;
2) 计算rk的协方差矩阵Drk= HPk, k-1HT,检验量Δrk= rkTDrk-1rk;
3) 对于给定阈值C,当Δrk < C,认为新观测值不包含粗差,否则认为新观测值包含粗差,修正观测值协方差矩阵
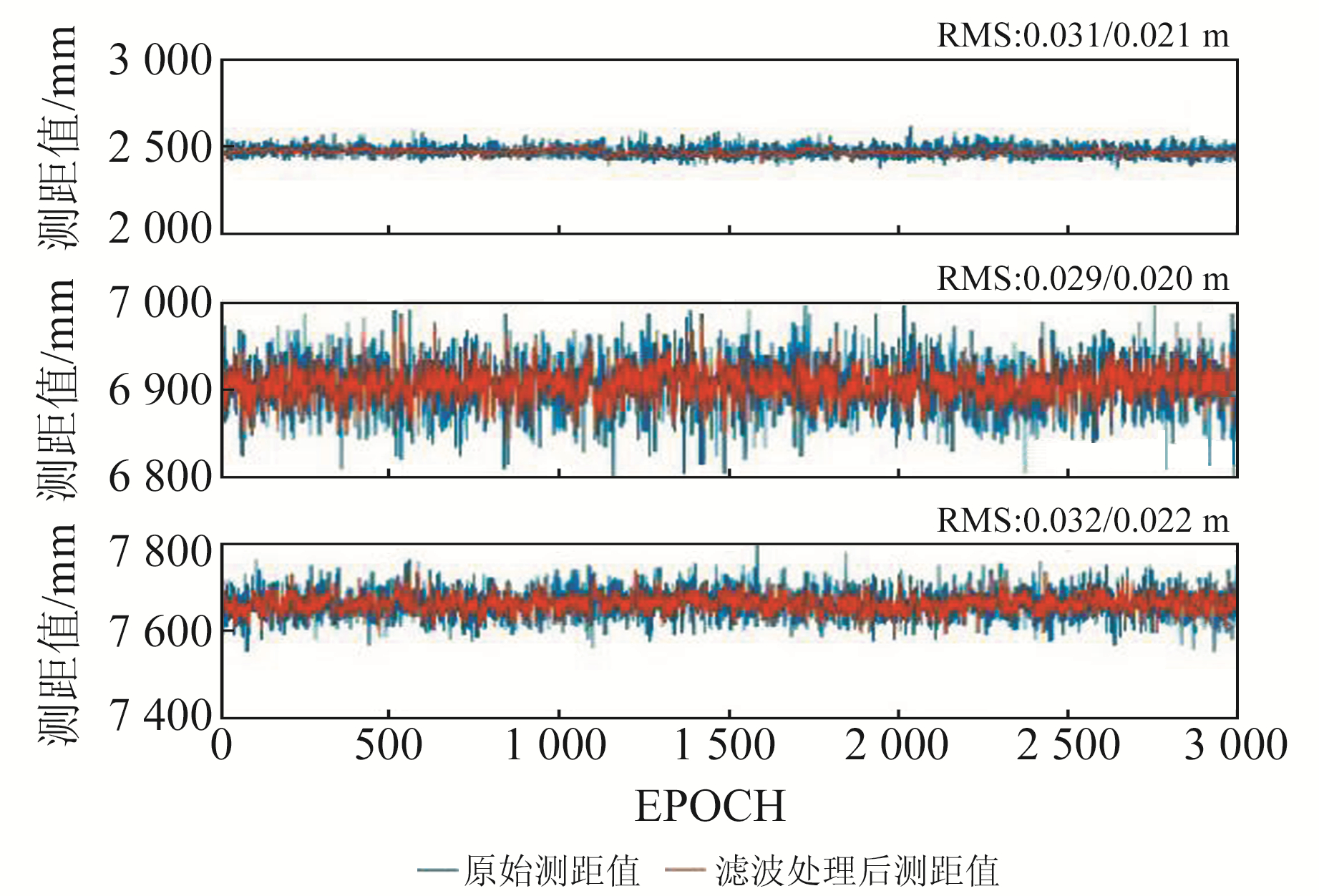
图 3展示了用上述方法处理TOF原始测量值的效果,图中蓝色线条为原始距离值,红色为滤波处理后的距离值。从图中可以直观地看出,处理后TOF距离值波动更小,RMS相比原始TOF距离值减小30%左右。
|
图 3 卡尔曼滤波降噪效果 Fig. 3 Noise reduction effects of Kalman filter |
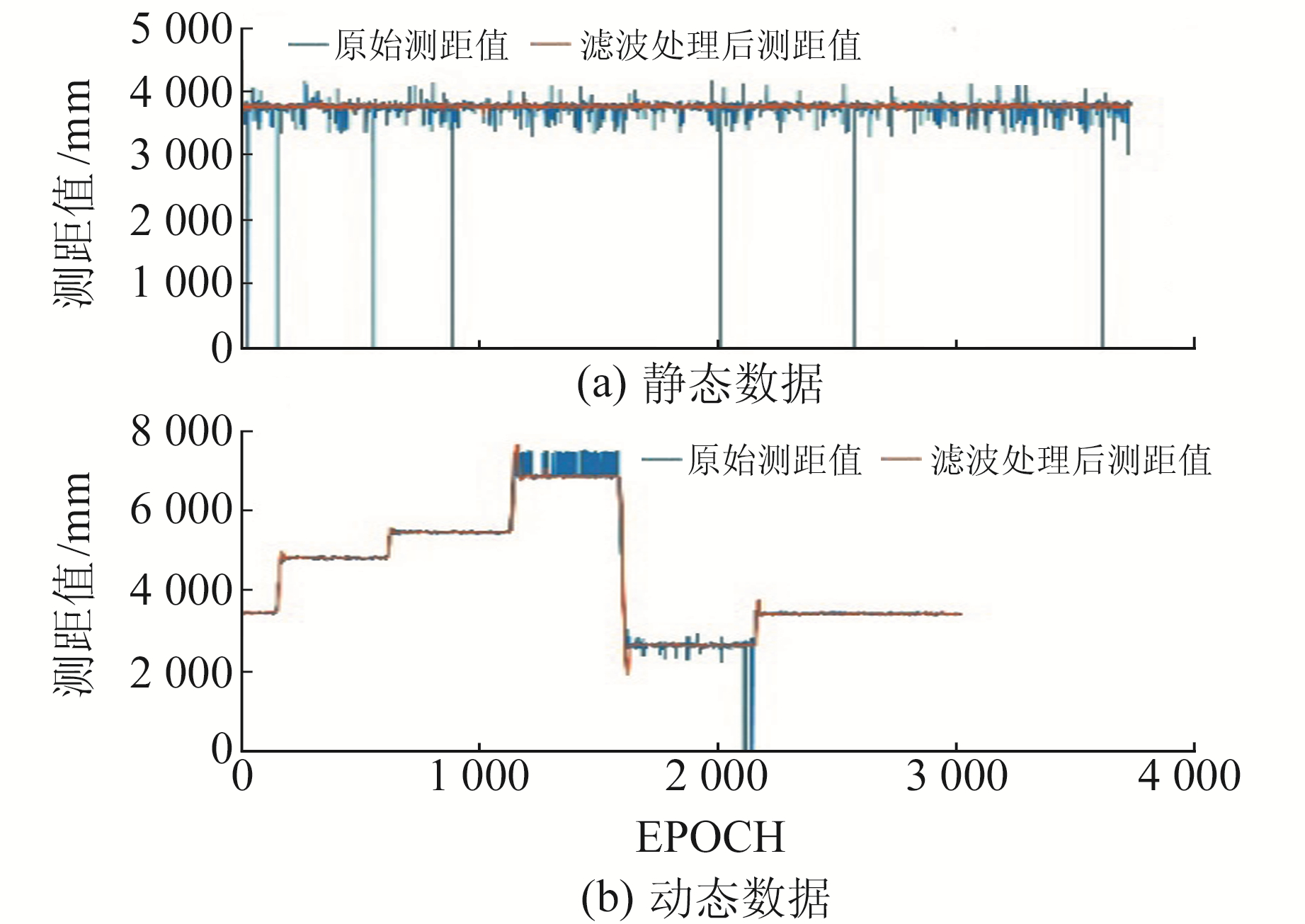
为了检验上述方法探测与剔除粗差的能力,从采集的原始数据中选择有明显粗差的一组,抗粗差效果如图 4(a)所示。可以看出,滤波后粗差得到了很好的抑制。此外,从图 4(b)可以看出,该方法对动态过程的TOF测距也有很好的降噪效果。
|
图 4 卡尔曼滤波抗粗差效果 Fig. 4 Anti-bias effects of Kalman filter |
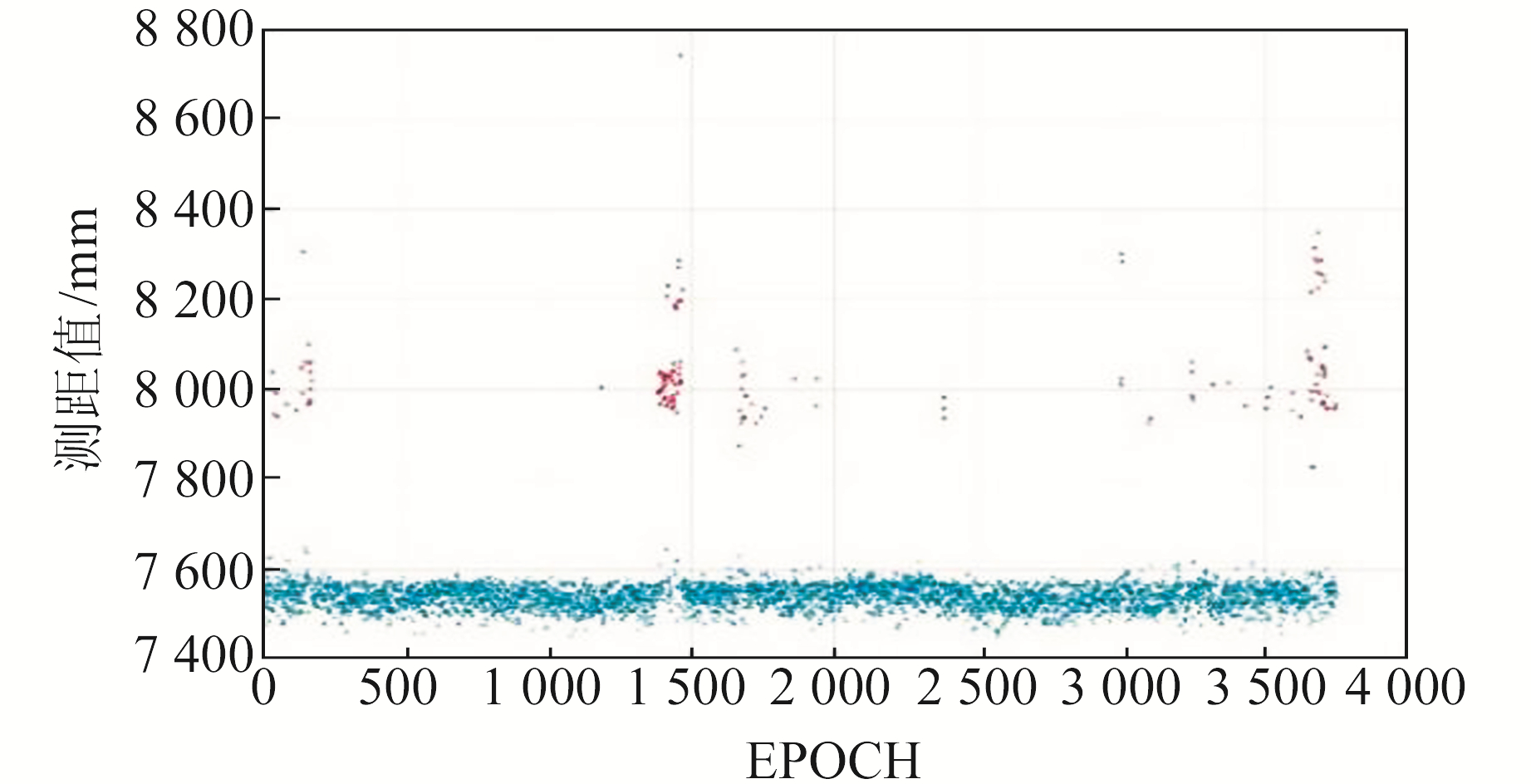
多径效应与NLOS环境是影响测距精度的主要因素。图 5是当标签贴近墙壁时,受多径效应影响的TOF测距值。可以看出,测距值中出现了部分明显的离群值(红色点),这部分异常值可以作为粗差,利用§2.1中的抗差滤波方法予以剔除,但群值(图中蓝色点)的分布范围比正常环境下的测距分布要大,这也是多径效应的典型现象。
|
图 5 多径效应对TOF测距的影响 Fig. 5 Multi-path effects on TOF measuring |
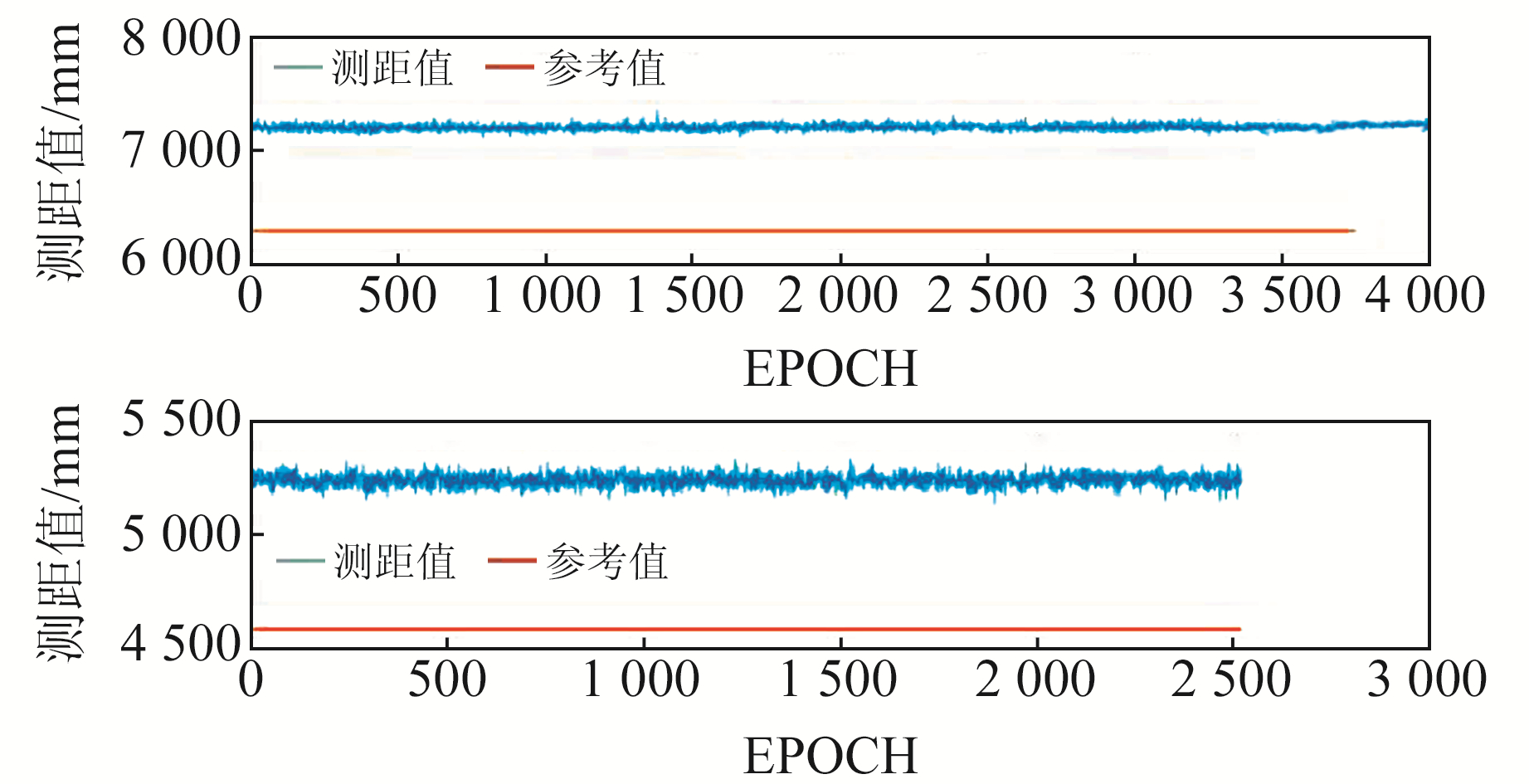
为了具体了解NLOS误差,将标签固定在与基站形成NLOS环境的2个位置上采集数据,将UWB测距值与参考值对比,结果见图 6。由图可见,2组TOF测量值分别偏高约0.9 m和0.7 m。这一偏差并非仅由NLOS环境引起,还包括UWB设备的天线延迟等,但NLOS环境为主要原因,这对定位精度的影响很大,实际应用中必须考虑NLOS误差并有相应的应对策略。本文提出一种应对墙壁等静态目标的NLOS环境的策略,这一策略的主要思想为:对复杂的室内场景进行分块,每一个子块内的基站均对整个子块空间保持通视,以此降低NLOS误差。以图 7的“L”型空间为例,具体步骤如下:
|
图 6 NLOS环境下观测值与真值对比 Fig. 6 Observed and true value under NLOS |
|
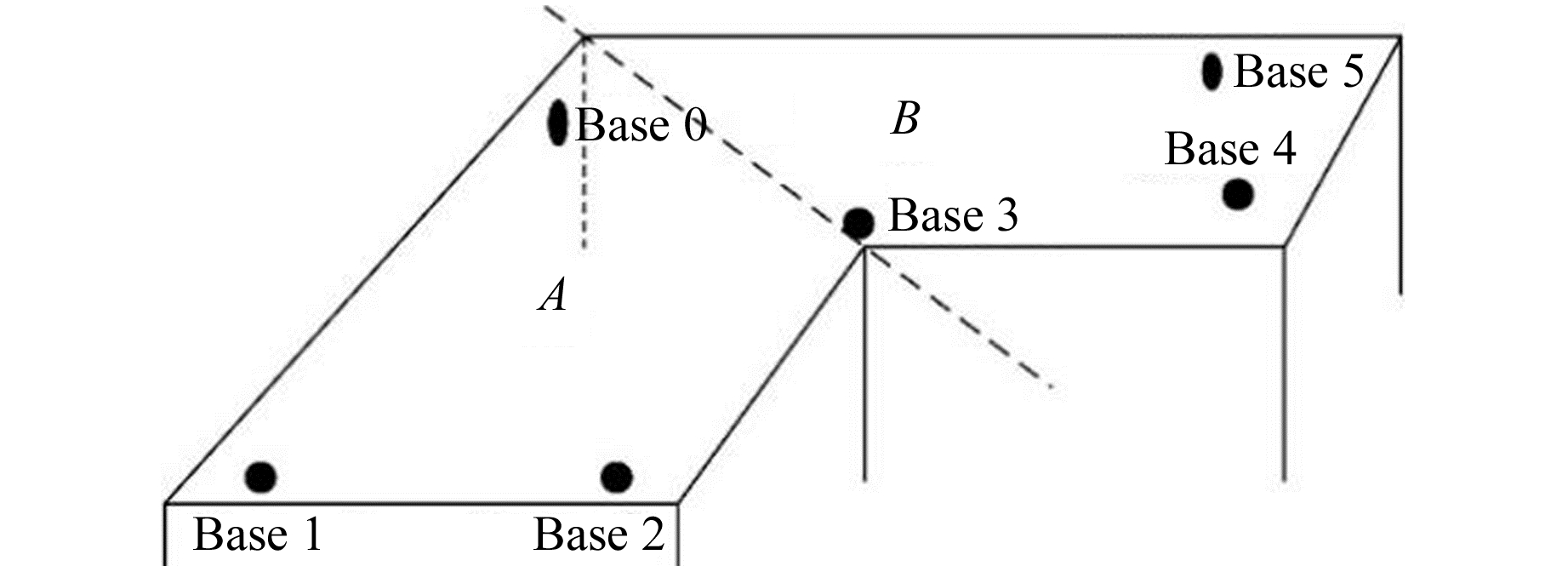
图 7 “L”型空间及划分 Fig. 7 "L" shaped space and partitioning |
1) 在空间内布设6个基站Base 0~Base 5;
2) 以虚线为界将空间划分成A和B 2个子块,标签位于A中时,只用Base 0、1、2、3定位,位于B中时只用Base 0、3、4、5定位;
3) 利用所有基站测距值初始化标签位置,判断标签位于哪一子块内并选择相应基站;
4) 标签所在子块发生变化时,更换相应基站。
以“L”型空间为例用上述方法进行分块,对于更复杂的室内场景,在应用该方法时要仔细地进行区域划分,做到在充分利用基站的同时规避NLOS环境。
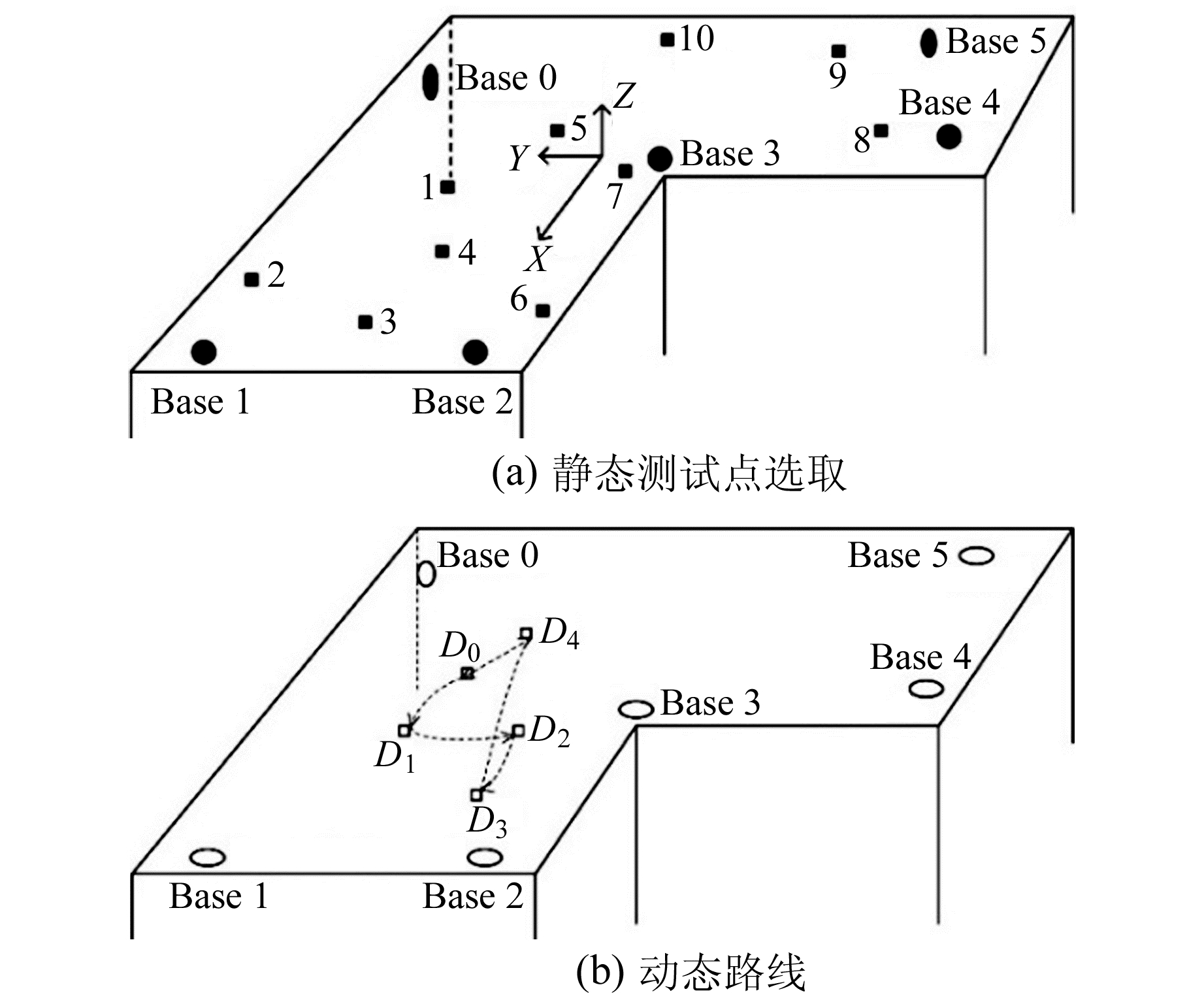
3 定位模型及精度验证实验在一个“L”型空间内进行,6个基站布置在靠近墙角的区域(图 8)。图 8(a)中1~10为选取的10个静态测试点,在每个测试点上采集约10 min数据。图 8(b)为动态定位的点位选取与运动轨迹,测试点D0~D4与基站保持通视且远离墙壁以减小NLOS和多径的影响。实验时,标签从D0出发,依次经过D1~D4并在每个点位上停留1 min左右,最终返回D0。利用全站仪建立室内自定义坐标系,坐标系原点与方向如图 8(a)所示,并精确测量基站与所有测试点的坐标,其精度可达mm级,能够作为UWB定位结果的参考值。
|
图 8 基站布置与测试点选取 Fig. 8 Layout of base stations and selection of test points |
利用卡尔曼滤波逐历元解算标签状态,对于静态定位,选取标签位置X =[x y h]T作为系统状态;对于动态定位,将系统状态扩展为标签位置及其变化率
| $ \boldsymbol{X}_{k}={\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \boldsymbol{X}_{k-1}+\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \boldsymbol{w}_{k} $ | (8) |
静态模式下认为不存在系统过程噪声,即wk视为0,动态模式下将标签加速度视为过程噪声,即
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}_{6 \times 6}=\left[\begin{array}{cc}\boldsymbol{I}_{3 \times 3} & \boldsymbol{D} T \\ 0 & \boldsymbol{I}_{3 \times 3}\end{array}\right], \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{6 \times 3}=\left[\begin{array}{c}0 \\ \boldsymbol{D} T\end{array}\right] $ |
系统观测方程:
| $ \boldsymbol{Z}_{k}=f\left(\boldsymbol{X}_{k}\right)+\boldsymbol{v}_{k} $ |
由于距离与位置间为非线性关系,因此在更新滤波时,需要线性化。为了获得较为理想的初始滤波信息,利用基站间差分法求标签的初始坐标,以基站0为参考:
| $ d_{0}=\sqrt{\left(x_{0}-x\right)^{2}+\left(y_{0}-y\right)^{2}+\left(h_{0}-h\right)^{2}}+v_{0} $ | (9) |
对式(9)两边平方并忽略误差项得:
| $ d_{0}^{2}=x^{2}+y^{2}+h^{2}-2 x_{0} x-2 y_{0} y-2 h_{0} h+l_{0}^{2} $ | (10) |
式(10)中,l02=x02+y02+h02。其他基站观测方程与基站0差分消除二次项:
| $ \begin{array}{c} -2\left(x_{i}-x_{0}\right) x-2\left(y_{i}-y_{0}\right) y- \\ 2\left(h_{i}-h_{0}\right) h=d_{i}^{2}-d_{0}^{2}-\left(l_{i}^{2}-l_{0}^{2}\right) \end{array} $ | (11) |
理论上,当基站数量不少于4即可用最小二乘法解出标签坐标。需要注意的是,由于基站布设的高度相近,方程中hi-h0项近似于0,最小二乘求解时法方程趋于病态,导致求出的高度坐标h误差很大。为了减小误差,可以利用几何关系求解较为准确的标签h坐标:
| $ h=\frac{1}{n} \sum\limits_{i=1}^{n}\left(h_{i}-\sqrt{d_{i}^{2}-x^{2}-y^{2}}\right) $ | (12) |
得到初始坐标值后,即可初始化滤波器逐历元更新系统状态。
3.2 定位精度验证表 1为静态定位滤波稳定后的结果与参考坐标的RMS,可以看出,10组样本中有6组水平位置误差在10 cm以内。其余组结果中,精度最差的点2的X坐标偏差超过0.2 m、Y坐标偏差超过0.3 m;点6的水平偏差超过0.24 m;点8也存在超过0.27 m的水平误差。这3个测试点均处在受多径效应或NLOS环境影响严重的区域,这与§2.2中的结论一致。剩下一组9号点误差略微超过10 cm,原因是其与2号基站间的NLOS环境引入了系统误差,导致其比其他通视良好的测试点定位精度要差。
|
|
表 1 静态定位测试点误差 Tab. 1 Error of static positioning |
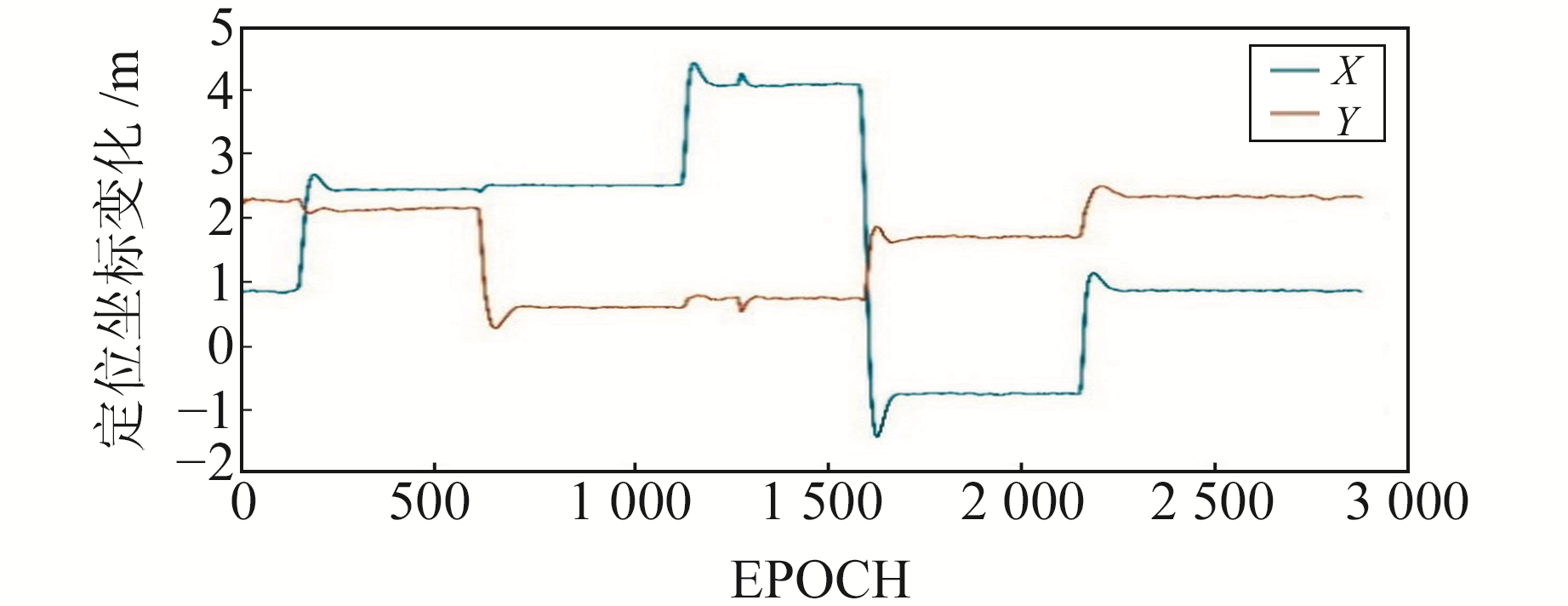
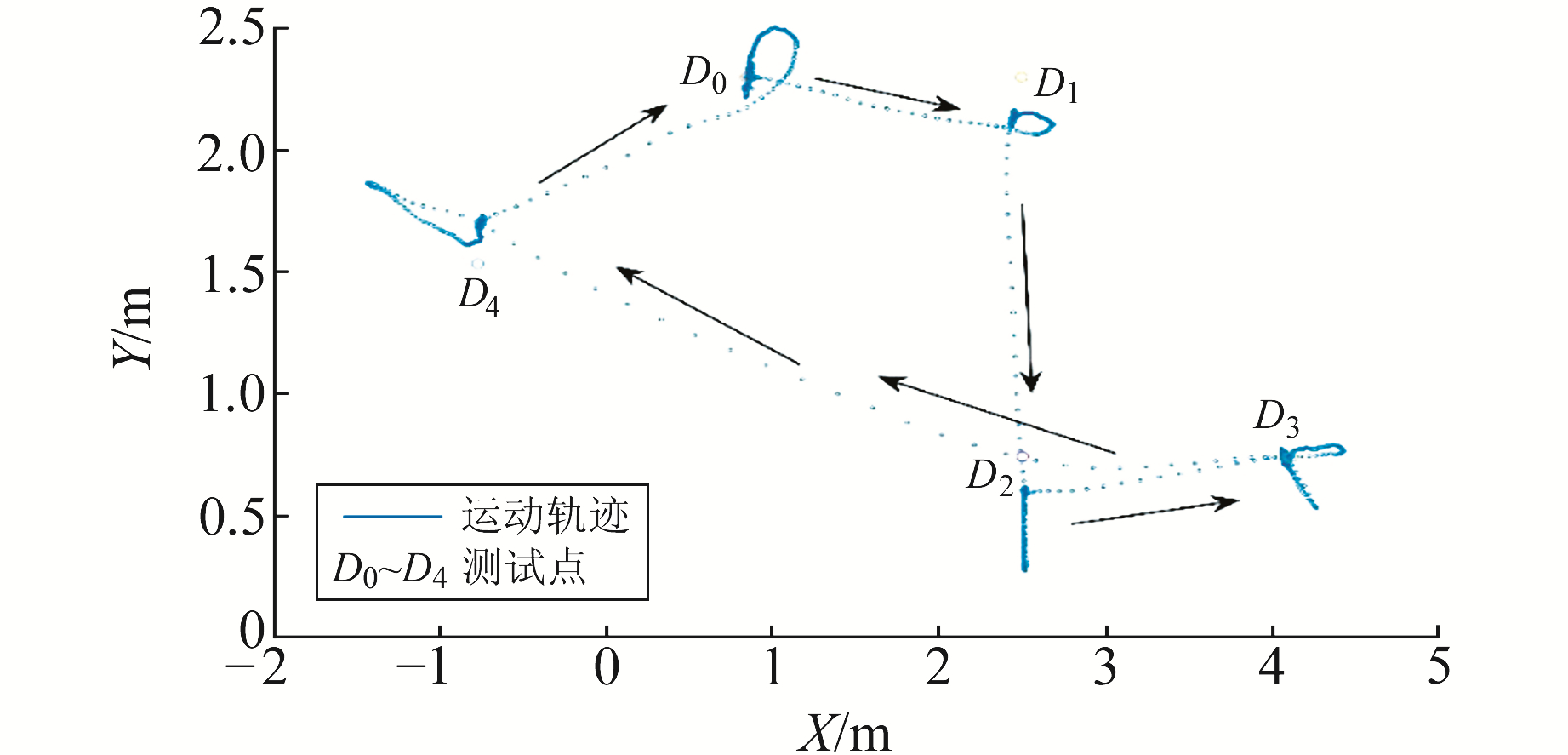
图 9绘出了平面X、Y坐标的变化,可以看出,除了在D3停留时出现短暂波动,标签在每个测试点停留的过程中定位结果都能保持相对稳定。图 10展示了标签的运动轨迹,D0~D4为测试点准确坐标。由图可见,精度较差的点位(如D1和D4)误差约20 cm,D0和D3点位精度在cm级,D2点位精度介于两者之间。为了得到准确的定位误差,对每个测试点滤波收敛后的一段结果取均值并与准确值计算残差(表 2),可以看出,测试点X坐标精度均在5 cm以内、Y坐标误差最大约17 cm。
|
图 9 动态定位水平坐标变化 Fig. 9 Changes of horizontal location in dynamic positioning |
|
图 10 平面动态轨迹 Fig. 10 Horizontal motion trail |
|
|
表 2 动态定位测试点误差 Tab. 2 Error of dynamic positioning |
本文详细推导基于双边双向测距(DS-TWR)的TOF测距原理,提出利用滤波方法探测、剔除测距粗差与降低噪声水平,进一步验证分析NLOS环境与多径效应对TOF测距的影响,设计基于卡尔曼滤波的静态与动态UWB定位方法并进行验证。结果证明:
1) 原始TOF测距经过滤波处理后,测距粗差能得到有效的剔除,测距值RMS由原始测量值的约3 cm提升至约2 cm。
2) 静态定位结果中,受多径效应与NLOS环境影响严重的区域水平精度降至约0.4 m,其他区域水平精度基本优于10 cm。
3) 对于动态定位,由于选取的区域通视条件较好且多径效应干扰较弱,滤波稳定后的水平精度优于0.2 m,部分点位水平精度可达10 cm左右。
| [1] |
Alarifi A, Al-Salman A, Alsaleh M, et al. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances[J]. Sensors, 2016, 16(5): 1-36 DOI:10.1109/JSEN.2015.2509619
(  0) 0) |
| [2] |
席瑞, 李玉军, 侯孟书. 室内定位方法综述[J]. 计算机科学, 2016, 43(4): 1-6 (Xi Rui, Li Yujun, Hou Mengshu. Survey on Indoor Locationing[J]. Computer Science, 2016, 43(4): 1-6)
(  0) 0) |
| [3] |
Chen L, Pei L, Kuusniemi H, et al. Bayesian Fusion for Indoor Positioning Using Bluetooth Fingerprints[J]. Wireless Personal Communications, 2013, 70(4): 1735-1745 DOI:10.1007/s11277-012-0777-1
(  0) 0) |
| [4] |
陈国良, 张言哲, 汪云甲, 等. WiFi-PDR室内组合定位的无迹卡尔曼滤波算法[J]. 测绘学报, 2015, 44(12): 1314-1321 (Chen Guoliang, Zhang Yanzhe, Wang Yunjia, et al. Unscented Kalman Filter Algorithm for WiFi-PDR Integrated Indoor Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1314-1321 DOI:10.11947/j.AGCS.2015.20140691)
(  0) 0) |
| [5] |
牛群峰, 曹一帆, 王莉, 等. 基于TW-TOF的UWB室内定位技术与优化算法研究[J]. 自动化与仪表, 2018, 33(1): 5-9 (Niu Qunfeng, Cao Yifan, Wang Li, et al. Study of UWB Indoor Positioning Technology and Optimization Algorithm Based on TW-TOF[J]. Automation and Instrumentation, 2018, 33(1): 5-9)
(  0) 0) |
| [6] |
Xu B, Sun G D, Yu R, et al. High-Accuracy TDOA-Based Localization without Time Synchronization[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(8): 1567-1576 DOI:10.1109/TPDS.2012.248
(  0) 0) |
| [7] |
Feng C, Au W S A, Valaee S, et al. Received-Signal-Strength-Based Indoor Positioning Using Compressive Sensing[J]. IEEE Transactions on Mobile Computing, 2012, 11(12): 1983-1993 DOI:10.1109/TMC.2011.216
(  0) 0) |
| [8] |
Guvenc I, Chong C C, Watanabe F. NLOS Identification and Mitigation for UWB Localization Systems[C]. Wireless Communications and Networking Conference, Hong Kong, 2007
(  0) 0) |
| [9] |
刘韬, 徐爱功, 隋心. 基于自适应抗差卡尔曼滤波的UWB室内定位[J]. 传感技术学报, 2018, 31(4): 567-572 (Liu Tao, Xu Aigong, Sui Xin. Adaptive Robust Kalman Filtering for UWB Indoor Positioning[J]. Chinese Journal of Sensors and Actuators, 2018, 31(4): 567-572 DOI:10.3969/j.issn.1004-1699.2018.04.013)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


