2. 华东交通大学土木建筑学院,南昌市双港东大街808号,330013;
3. 轨道交通工程信息化国家重点实验室,西安市西影路2号,710043
大多数基于EMD降噪的研究采用相关系数准则确定分界IMF函数[1-6],取互相关系数达到第1个局部极小值时的IMF作为分界IMF,而不能直接给出分界IMF函数的K值,且这些研究都是将低频有用分量进行累加重构实现降噪目的,未考虑高频噪声与低频信号IMF分量的个数差异对计算量的影响。本文基于EMD方法,提出一种降噪的新思路,采用平均周期与能量密度乘积指标的方法来自动地确定分界IMF的K值,并与相关系数准则所确定的分界IMF进行对比,验证该方法的准确性。针对IMF低频信号分量个数多于高频噪声分量个数的情况,将噪声分量进行重构,然后从原始信号中扣除重构的噪声,从而达到降噪的目的。
1 EMD降噪理论的改进根据EMD降噪的基本原理[7]可知,将低频IMF分量进行重构,能够达到降噪的目的。然而,当分界IMF之下的低频模态分量个数多于高频IMF噪声分量的个数时,直接重构会增加计算量,甚至会带入少量的系统误差。针对该问题,本文提出一种新的思路来获得降噪后的“干净”信号,可以减少计算量。原始数据经EMD分解后,从原始数据序列中减去重构后的高频噪声分量,得到“干净”信号。降噪信号的表达式为:
| $ \hat{x}(t)=x(t)-\sum\limits_{k=1}^{K} \operatorname{IMF}_{k} $ | (1) |
式中,x(t)为原始序列,
此外,考虑到利用相关系数准则确定分界IMF的复杂性,以及不能直接给出分界IMF函数的K值,本文在张恒璟等[8]的基础上,利用平均周期(Tk)与能量密度(Ek)的乘积(ETk)作为指标,给出一种自动确定分界IMF的算法,能够直接完成分界IMF函数K值的确定[8]。
信号与噪声分界点确定的阈值表达式为:
| $ R_{k-1}=\left|\frac{E T_{k}}{\left(\frac{1}{k-1} \sum\limits_{i=1}^{k-1} E T_{i}\right)}\right| $ | (2) |
式中,k≥2,当Rk-1≥C(本文中C取2)时,则判定k为分界点,文中N为各个模态的数据长度。将前k-1个噪声主导的模态分量进行重构,用原始数据序列减去重构的噪声,得到降噪后的信号。
利用相关系数(ρ)、均方根误差(RMSE)、信噪比(Rsn)等传统评价指标来衡量去噪的效果[9]。相关系数越接近1,降噪信号与原始数据序列的相似度越高,拟合效果越好,去噪效果也就越好;均方根误差体现了降噪信号与原始信号之间的偏差程度,值越小,去噪效果越好;信噪比主要是体现噪声信号在整体信号中的比重,其值越大,去噪效果越好。
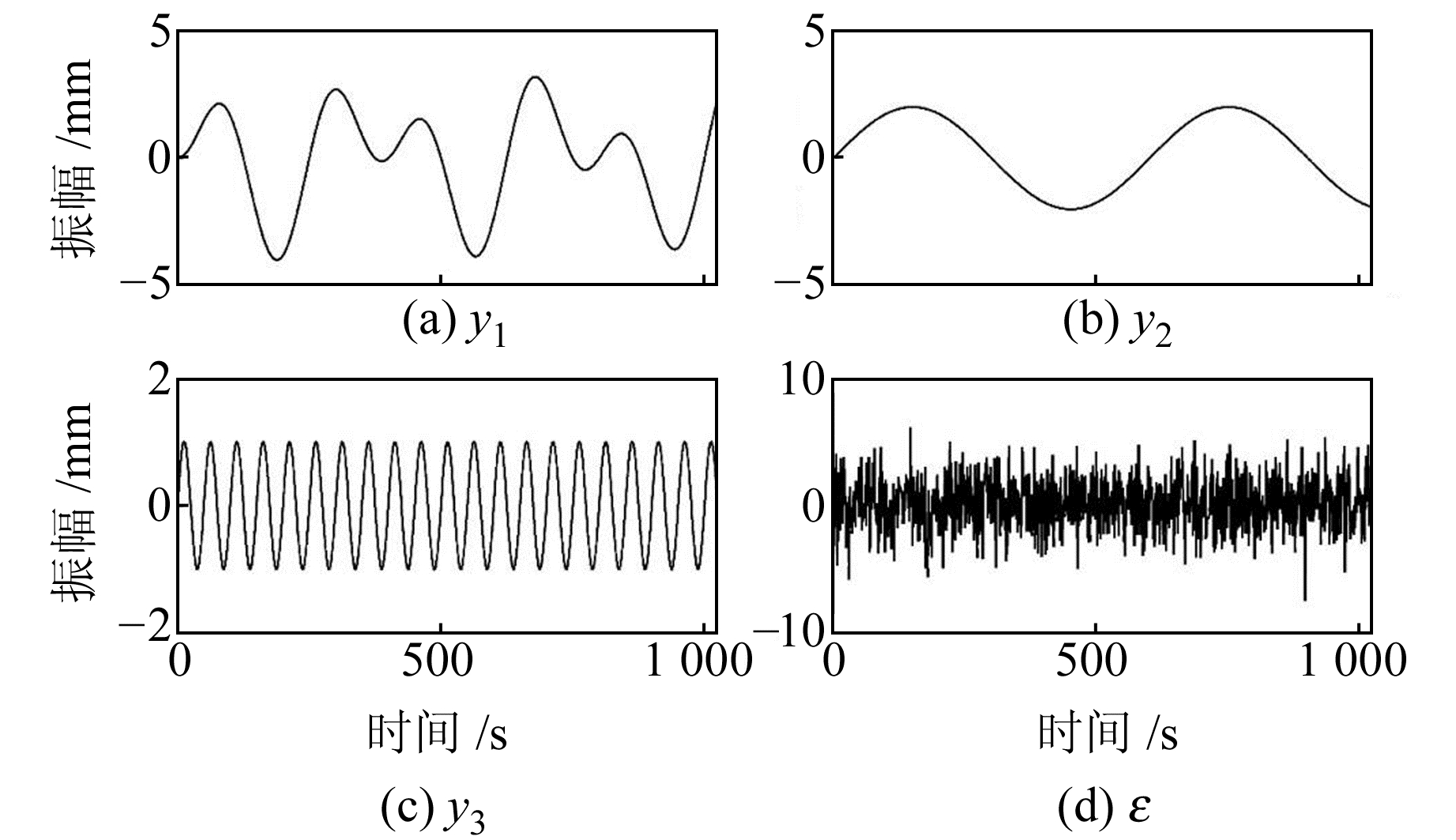
2 模拟数据降噪分析由于实测数据含有误差,首先采用真值已知的模拟信号对本文的方法进行验证。模拟信号的采样频率为1 Hz,采样点数为1 024个,noise是信噪比为4 dB的高斯白噪声,其构成分量信号波形图如图 1所示,加噪后所得的模拟原始信号及其频谱图如图 2所示。模拟数据可用式(3)表示:
| $ \left\{\begin{array}{l} y_{1}=4 \sin \left(\frac{2 \pi t}{800}\right) \sin \left(\frac{2 \pi t}{250}\right) \\ y_{2}=2 \sin \left(\frac{2 \pi t}{600}\right) \\ y_{3}=\sin \left(\frac{2 \pi t}{50}\right) \\ \varepsilon=\text { noise } \\ x=y_{1}+y_{2}+y_{3}+\varepsilon \end{array}\right. $ | (3) |
|
图 1 构成模拟信号的各分量信号波形 Fig. 1 Waveforms of components constituting analog signals |

|
图 2 加噪模拟原始信号及其频谱 Fig. 2 Noise-added analog original signal and spectrogram |
利用相关系数准则确定模拟信号的噪声与信号的分界IMF,计算的各IMF分量与模拟加噪数据序列之间的相关系数如图 3所示。由图 3可知,第4个IMF分量第1次取得局部极小值,所以将前4个分量视为高频噪声,从原始加噪数据序列中剔除高频噪声,获得降噪后的纯净数据序列。

|
图 3 各分量与原始信号所求得的相关系数 Fig. 3 The correlation coefficient between each component and the original signal |
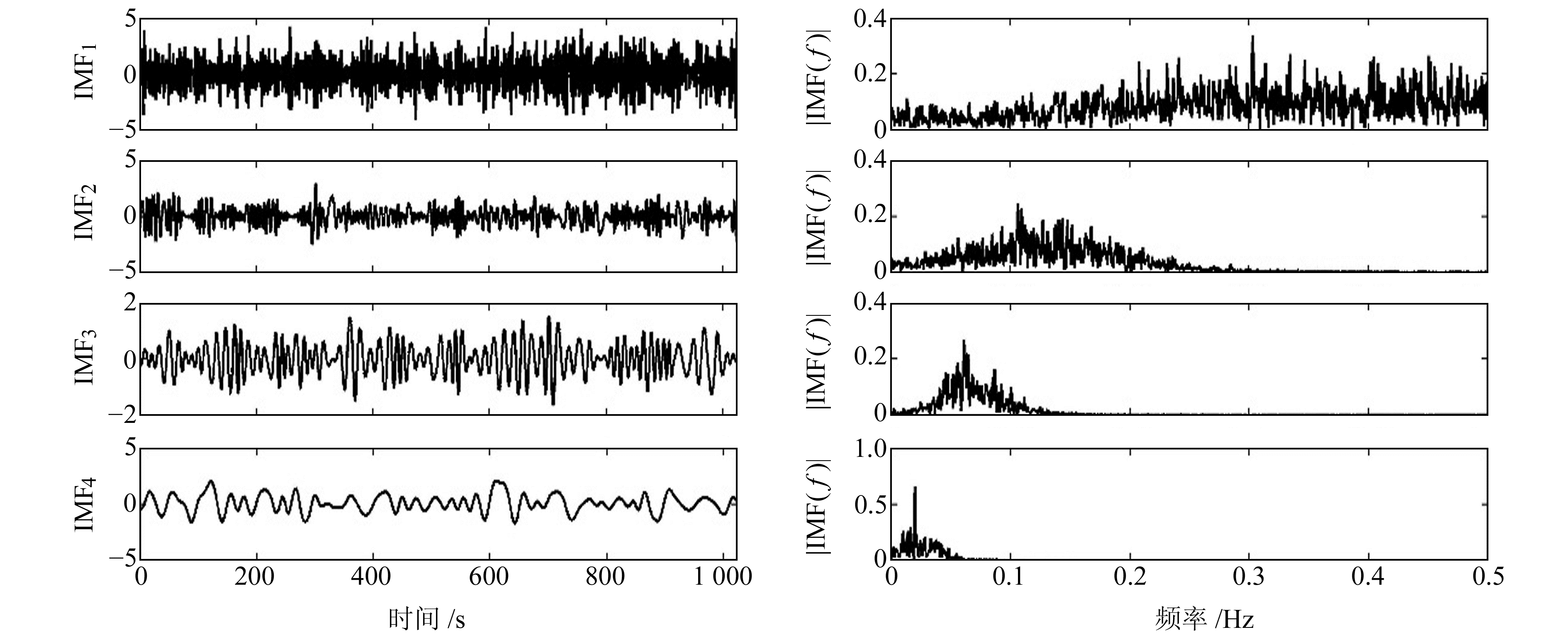
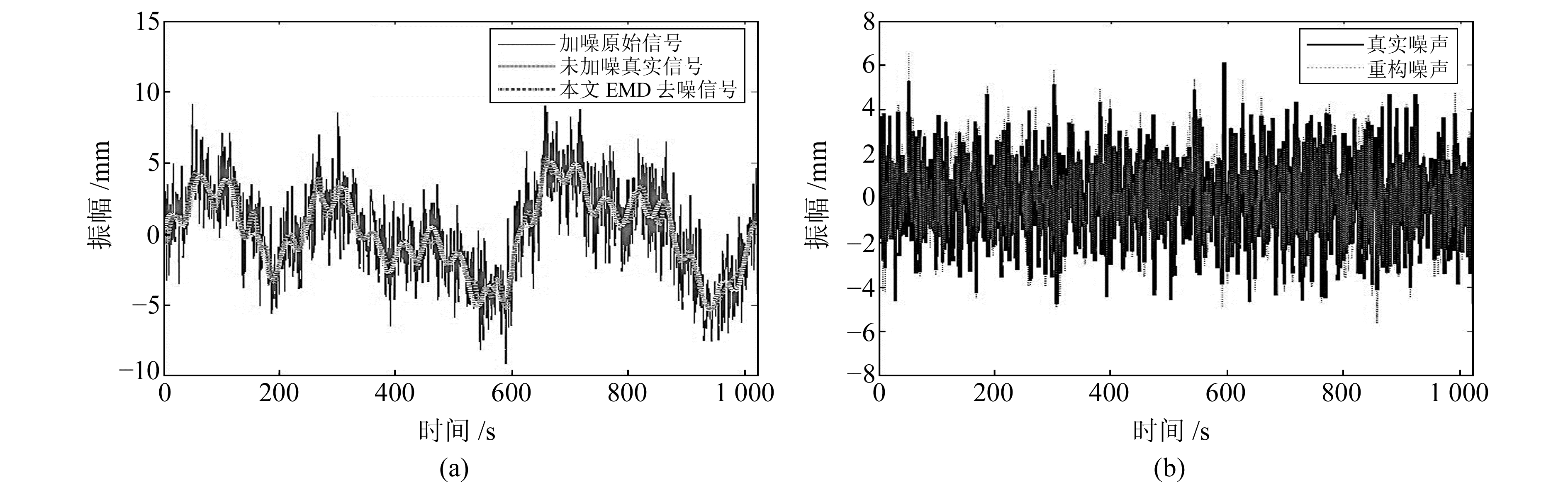
采用平均周期与能量密度的乘积指标(ETk)确定分界IMF,所得到的平均周期与能量密度以及ETk如表 1所示。由表 1可知,IMF1~IMF3 3个分量平均周期与能量密度的乘积指标的均值为5.817,而IMF4的指标为19.159,明显大于均值的2倍,将前3个分量视为高频噪声分量。本文方法确定分界IMF的K值时,所计算的R值分别为0.600,0.728,3.293,此时的K值为4,即前3个IMF分量为高频噪声,剩余的分量为低频真实信号。本文给出部分IMF分量的波形图及其对应的频谱,如图 4所示。图 5(a)为利用本文方法所得的重构去噪信号与原始不加噪的模拟信号对比图,图 5(b)为重构噪声与真实噪声的对比图。从图 5(a)中可看出,本文方法去噪后信号波形图与真实未加噪信号波形图拟合效果较好,图 5(b)中重构噪声与真实模拟噪声图基本吻合,验证了本文方法用于降噪的可靠性。
|
|
表 1 IMF分量平均周期与能量密度 Tab. 1 Average period and energy density of IMF component |
|
图 4 IMF1~IMF4分量的波形图及其频谱 Fig. 4 Waveform and spectrum of IMF1~IMF4 components |
|
图 5 信号及噪声对比 Fig. 5 Signal and noise contrast |
由于本文方法确定分界IMF函数的K值与相关系数准则所得结果不同,分别计算2种方法所得“干净”信号与真实未加噪信号的相关系数、均方根误差及信噪比,所得结果如表 2所示。表 2中,RPN1表示真实信号与原始信号的各评价指标,DPN1表示降噪信号与原始信号的各评价指标,DPR1表示本文方法所得降噪信号与真实信号的各评价指标,DPR2表示采用相关系数准则所得降噪信号与真实信号的各评价指标。由表 2可知,相较于DPN的各评价指标值,DPN1中ρ值与Rsn值更大,而RMSE值更小,说明本文方法降噪效果较优;与DPR2中的各指标值相比,DPR1中ρ值与Rsn值更大,而RMSE值更小,表明本文方法确定的分界IMF函数降噪效果优于相关系数准则。综合表 2中的各项指标值,验证了本文方法降噪效果的可靠性。
|
|
表 2 各评价参数值 Tab. 2 Values of each evaluation parameter |
根据本文方法所确定的分界IMF函数的K值可知,本文所模拟的加噪原始数据序列的低频真实信号分量的个数明显大于高频噪声分量的个数,采用传统方法直接利用低频信号进行去噪信号重构需要累加6N1(N1表示模拟数据的长度)次;而本文方法只需将前3个高频噪声分量进行累加,需2N1次运算,加上N1次减法运算,总共只需3N1次运算,明显比直接重构得到“干净”信号的计算量要少。综上所述,在模拟数据降噪分析中,本文方法能够自动确定分界IMF函数的K值,较之相关系数准则法降噪效果更精确,且能够减少计算量。
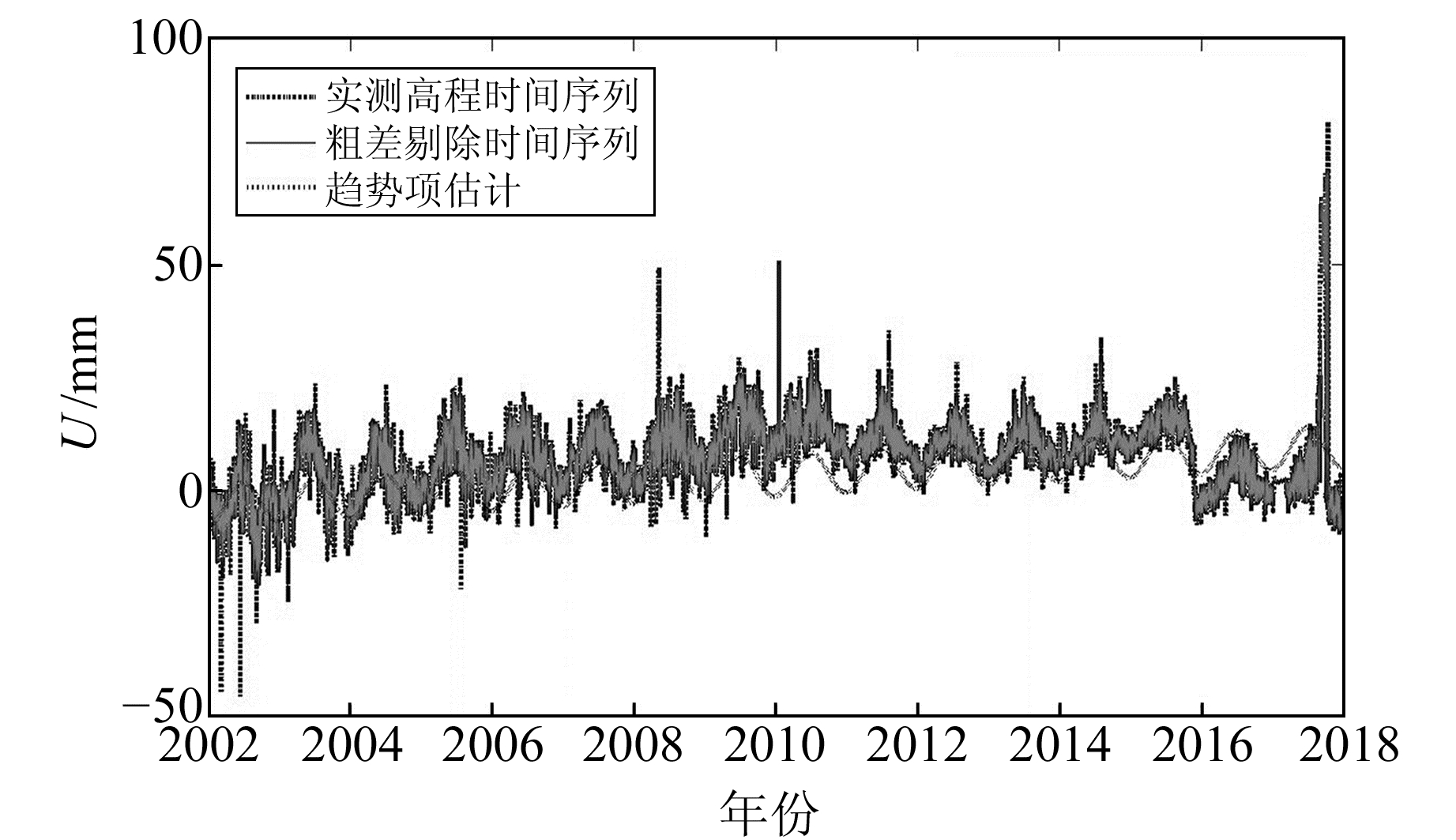
3 GPS实测高程时间序列降噪分析为了进一步验证本文方法的可靠性,使用北京房山(BJFS)站的实测高程(U)时间序列来进行降噪研究与分析。数据来自中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn/),时间跨度为2002~2018年,采样间隔为1/365.25年,最大采样频率为365.25 Hz。由于实测数据中含有一些粗差,进行分析之前利用Hector软件对序列中较大的粗差进行剔除,同时对剔除粗差之后的序列进行趋势项估计,将剔除粗差之后的坐标高程时间序列作为本文降噪分析的原始数据序列,所得结果如图 6所示。从图中可以看出,剔除粗差后的时间序列图的波动明显小于实测信号图,所估计的趋势项与U方向时间序列拟合效果也较好,且高程时间序列呈现出明显的周期性,说明确实达到了较好的剔除粗差的效果。
|
图 6 BJFS站高程时间序列 Fig. 6 Elevation time series of BJFS station |
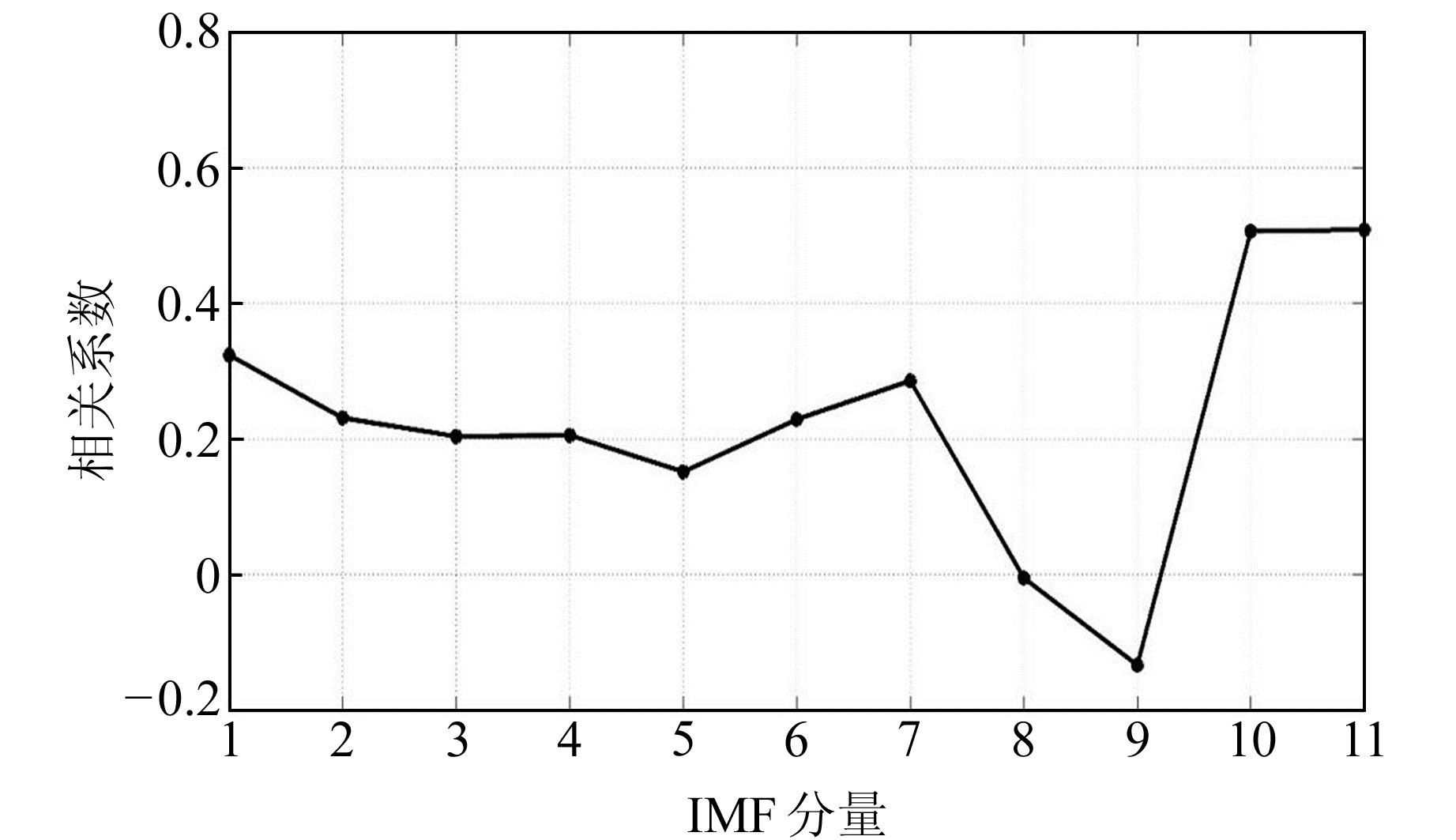
用EMD方法对BJFS站原始高程时间序列进行处理,得到11个本征模态分量(IMF),计算各IMF分量与剔除粗差之后的高程时间序列的相关系数,所得结果如图 7所示。从图中可以明显看出,第5个IMF与原数据序列的相关系数第一次取得局部极小值,即前5个高频IMF为噪声,剩余的为真实信号。
|
图 7 BJFS站高程方向各分量与原始信号所求得的相关系数 Fig. 7 Correlation coefficient of BJFS station elevation direction components and original signal |
利用各IMF分量的平均周期与能量密度的乘积指标确定分界IMF,所得结果如表 3所示。由表 3可知,前3个IMF分量的平均周期与能量密度的乘积指标(ETk)的平均值为29.842,IMF4的ETk指标为69.604,明显大于前3个IMF分量均值的2倍,即第4个IMF分量为分界IMF,前3个为高频噪声分量,剩余的IMF分量为真实信号。根据本文自动确定分界IMF分量K值的办法,在满足R阈值的情况下,R的取值依次分别为1.303 5,1.648 6,2.332 4,当R为2.332 4时停止筛选,此时自适应K值为4,即前3个IMF分量为噪声,后8个IMF分量为真实信号,此结果与利用相关系数所求得的结果不一致。为了比较本文方法与平均周期与能量密度指标方法确定分界IMF的准确性,并且对最后的降噪效果进行评价,分别利用2种不同结果重构后信号与原始信号的相关系数、均方根误差以及信噪比进行对比分析,结果如表 4所示。由表 4可知,本文算法在实测数据中能够直接给出分界IMF的K值,且相比于相关系数准则所得降噪信号,本文方法所得降噪信号与原始信号的ρ值与Rsn值更大,RMSE值更小,表明本文方法降噪效果比相关系数准则更佳。
|
|
表 3 实测数据IMF分量平均周期与能量密度 Tab. 3 Average period and energy density of IMF components from measured data |
|
|
表 4 各评价参数值 Tab. 4 Values of each evaluation parameter |
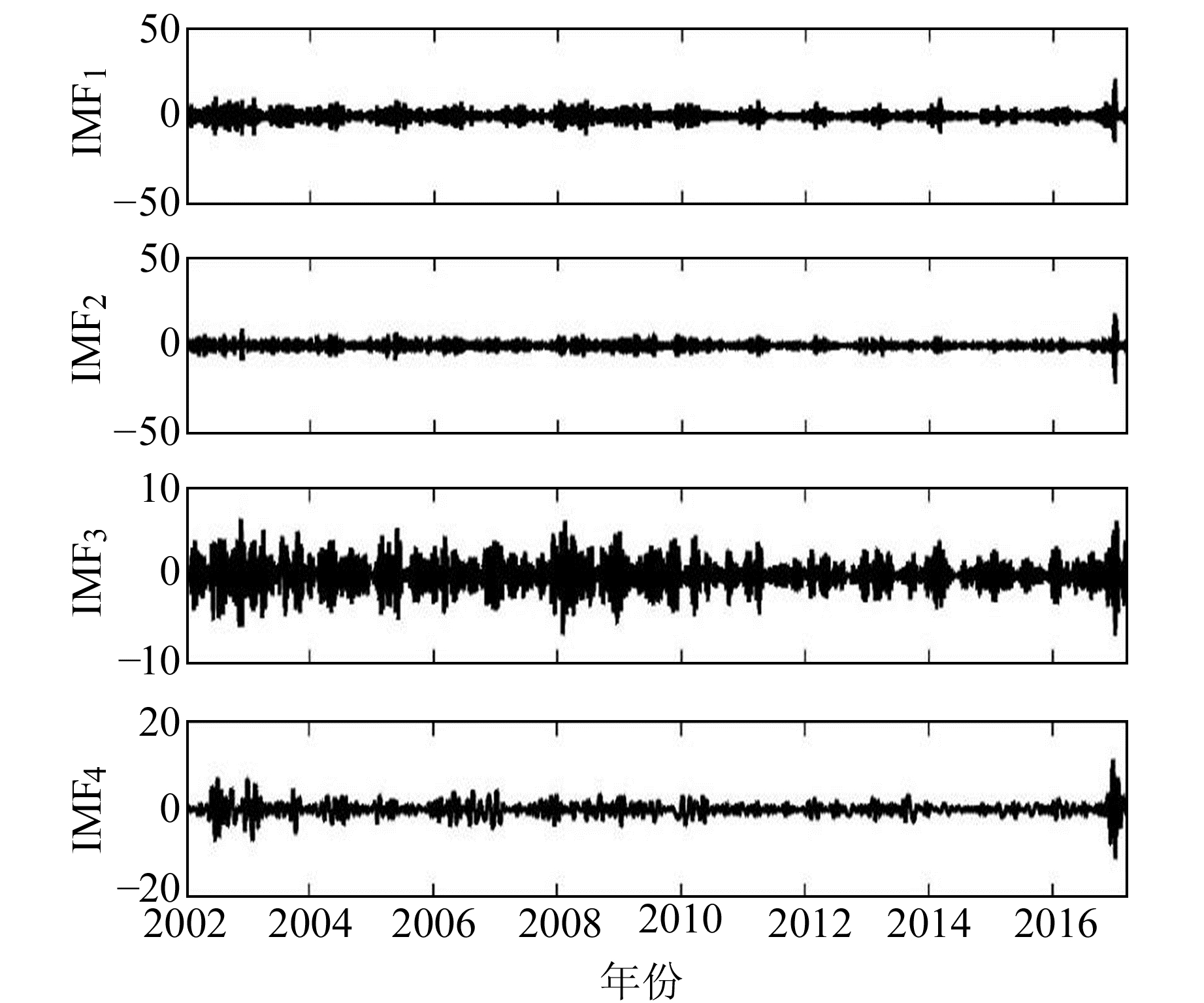
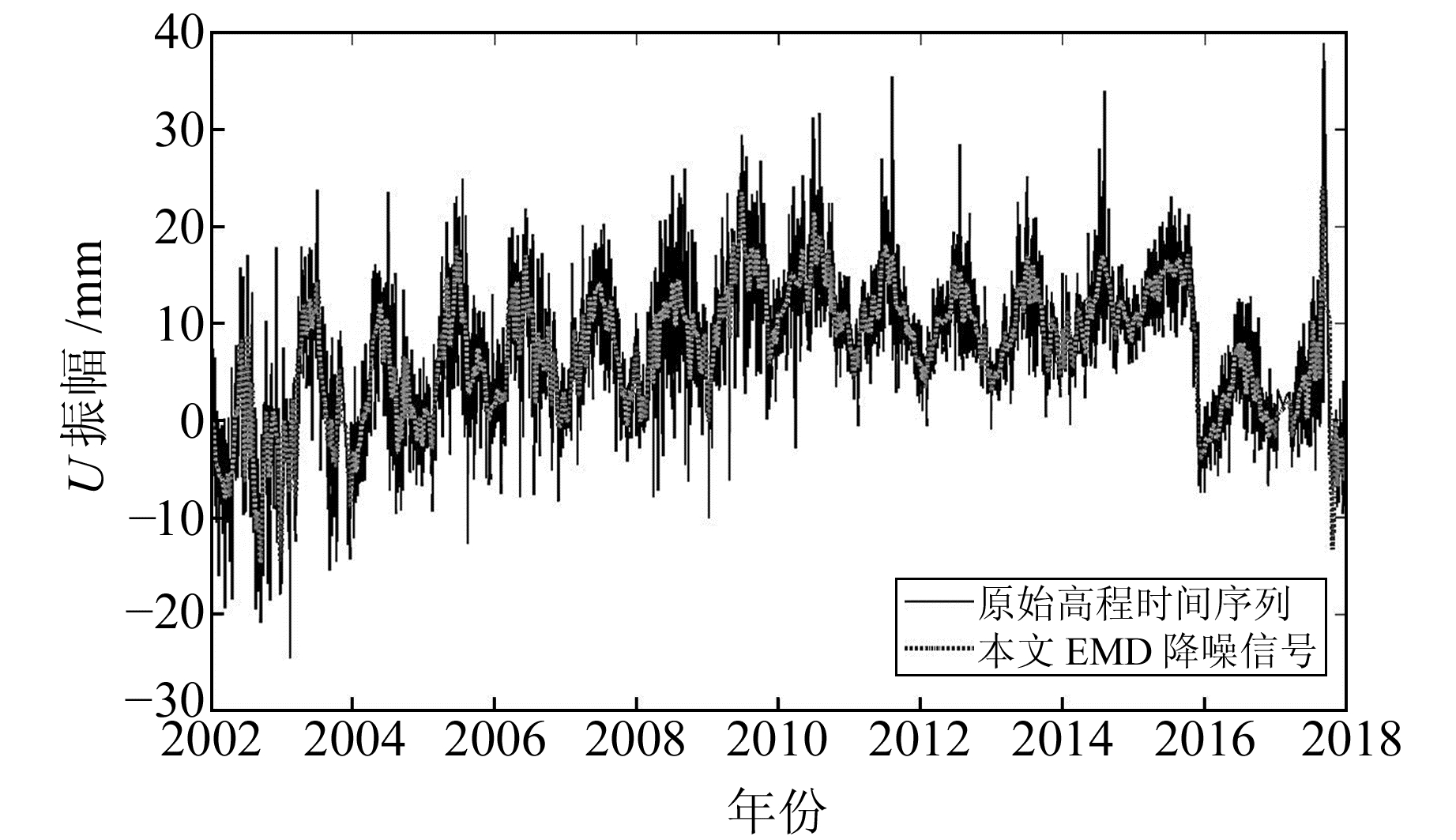
图 8给出了部分IMF分量的波形,前3个IMF分量为高频噪声,第4个IMF分量为分界IMF函数。根据本文提出的降噪思路,将前3个高频噪声分量进行重构,然后用原始高程时间序列减去重构后的高频噪声,得到降噪的高程时间序列,如图 9所示。由图 9可知,降噪后“干净”信号较之原始高程时间序列明显更清晰,验证了本文方法应用于GPS高程时间序列降噪的有效性。本文方法得到“干净”信号只需3N2(N2表示实测数据的长度)次运算,传统的EMD重构方法需要进行7N2次累加运算,减少了计算量。
|
图 8 BJFS站前4个分量波形 Fig. 8 Waveform charts of the first four components of BJFS station |
|
图 9 BJFS站原始高程时间序列与本文方法去噪所得时间序列 Fig. 9 BJFS station original elevation time series and the time series obtained by denoising in this paper |
本文在EMD降噪分解过程中,结合平均周期与能量密度乘积的指标,给出一种自动确定分界IMF分量K值的算法,并且与相关系数准则确定分界IMF分量的方法进行对比。模拟数据结果表明,本文算法所得的降噪信号较之相关系数准则所得降噪信号,相关系数提高0.017,RMSE减小0.156,信噪比提高5.142 dB。BJFS站的实测GPS高程时间序列结果表明,本文所提出的改进EMD方法较之传统EMD方法,相关系数提高0.04,均方根误差减小0.51 mm,信噪比提高3.14 dB。模拟数据和实测GPS高程时间序列数据的结果都表明,改进的EMD方法用于降噪分析精度优于传统EMD方法,是一种更为精确的降噪方法。
同时,本文针对EMD分解过程中高频噪声IMF分量的个数少于低频真实信号IMF分量的个数的情况,提出一种新的EMD降噪思路。模拟数据结果表明,本文的降噪方法相对于传统的直接重构算法,减少了4N1次累加运算。GPS实测高程时间序列结果表明,本文提出的新方法较之直接重构方法降噪,减少了4N2次累加运算。综上所述,本文所提出的基于EMD的GPS高程时间序列降噪新方法,能够自动确定分界IMF函数的K值,减少计算量。但是,当高频噪声IMF分量个数多于低频噪声分量个数时,该方法并不适用,且信号与噪声分界的阈值为经验值,需要对该阈值的选取展开进一步的研究。
| [1] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84 (Zhang Shuangcheng, Li Zhenyu, He Yuefan, et al. Extracting of Periodic Component of GNSS Vertical Time Series Using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84)
(  0) 0) |
| [2] |
张宁. 基于CEEMD阈值和相关系数原理的MEMS陀螺信号去噪方法[J]. 传感技术学报, 2018, 31(9): 1 383-1 388 (Zhang Ning. Signal De-Noising Method for MEMS Gyroscope Based on CEEMD Threshold and Correlation Coefficient Principle[J]. Chinese Journal of Sensors and Actuators, 2018, 31(9): 1 383-1 388)
(  0) 0) |
| [3] |
罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报:信息科学版, 2012, 37(4): 450-453 (Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 450-453)
(  0) 0) |
| [4] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1 013-1 023 (Jia Ruisheng, Zhao Tongbin, Sun Hongmei, et al. Micro-Seismic Signal Denoising Method Based on Empirical Mode Decomposition and Independent Component Analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 1 013-1 023)
(  0) 0) |
| [5] |
王文波, 张晓东, 汪祥莉. 基于独立成分分析和经验模态分解的混沌信号降噪[J]. 物理学报, 2013, 62(5): 27-34 (Wang Wenbo, Zhang Xiaodong, Wang Xiangli. Chaotic Signal Denoising Method Based on Independent Component Analysis and Empirical Mode Decomposition[J]. Acta Physica Sinica, 2013, 62(5): 27-34)
(  0) 0) |
| [6] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1 248-1 252 (Zhang Shuangcheng, He Yuefan, Li Zhenyu, et al. EMD for Noise Reduction of GPS Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1 248-1 252)
(  0) 0) |
| [7] |
张恒璟, 程鹏飞. 基于经验模式分解的CORS站高程时间序列分析[J]. 大地测量与地球动力学, 2012, 32(3): 129-134 (Zhang Hengjing, Cheng Pengfei. Analysis on Time Series of Two CORS Stations' Height Based on EMD[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 129-134)
(  0) 0) |
| [8] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [9] |
郭翔. EMD在GPS信号去噪中的应用研究[D].南昌: 东华理工大学, 2016 (Guo Xiang. Research on GPS Date Denoising Based on EMD[D].Nanchang: East China University of Technology, 2016)
(  0) 0) |
2. School of Civil Engineer and Architecture, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China;
3. State Key Laboratory of Rail Transit Engineering Informatization(FSDI), 2 Xiying Road, Xi'an 710043, China
 2020, Vol. 40
2020, Vol. 40


