2. 西南交通大学地球科学与环境工程学院,成都市高新区西部园区,611756
细颗粒物(PM2.5)的成分包含挥发性或半挥发性物质,易受气候环境的影响,而基于地基GNSS探测的大气可降水量(PWV)与大气温度和相对湿度有关,其变化在某种程度上可以反映大气水汽对PM2.5的影响[1-2]。为掌握PWV与PM2.5的关系,相关学者进行了大量研究[3-5],但这些研究大多将连续的PWV和PM2.5数据作为研究对象,计算Pearson积矩相关系数。由于连续数据中可能包含大量非雾霾天气,在讨论PWV和PM2.5之间的相关性时容易产生偏差,且连续数据中的缺失值及异常值也会影响相关性的分析结果。为深入准确地研究PWV和PM2.5之间的相关性,本文通过对北京市2014~2016年的城市空气质量进行对比分析,建立2个数据选取标准:时间标准和AQI等级标准。经过筛选,获取发生雾霾时的真实PWV变化情况,使PWV和PM2.5的相关性分析更具针对性。
需要注意的是,筛选后的数据并非连续等距,且数据的相关形式、分布类型均未知,若直接采用Pearson积矩相关系数进行分析,结果可能不准确[6]。因此,为提高相关性分析的可靠性,本文引入一种非参数性质的相关系数——Spearman秩相关系数,该相关系数对原始数据的选取、相关形式及分布类型均无要求,通常用于度量变量间单调相关或等级相关性的强弱,其通用性及稳健性较参数性质的Pearson积矩相关系数好[7-8]。
1 地基GNSS水汽反演方法地基GNSS反演水汽作为一种新的水汽探测方法,具有探测精度高、时空分辨率高、不受气候条件影响等特点[9-10],近年来已在气象领域获得广泛应用[11]。大气可降水量(PWV)定义为对流层中垂直方向气柱内的水汽含量全部折算成液态水的厚度,其与天顶湿延迟(ZWD)之间存在如下转化关系[12-13]:
| $ \mathrm{PWV}={\mathit{\Pi}} \times \mathrm{ZWD} $ | (1) |
| $ {\mathit{\Pi}}=\frac{10^{6}}{\rho_{w} R_{v}\left(k_{2}^{\prime}+k_{3} / T_{m}\right)} $ | (2) |
式中,ZWD为天顶湿延迟,Π为转换系数,ρw为液态水的密度,Rv为气体常数,k′2和k3为大气折射率常数,Tm为大气加权平均温度,可通过各种区域或全球经验模型[14-16]确定。地基GNSS反演水汽的具体过程为:1)利用GNSS观测资料反演得到高精度的对流层延迟序列[17-18],由对流层天顶方向的大气总延迟(ZTD)与静力延迟(ZHD)作差得到ZWD,ZHD可采用各种气象经验模型[19-21]进行计算;2)将得到的ZWD代入式(1)即可得到PWV值。
2 实验数据的选取及处理方案 2.1 研究数据选取北京市作为研究区域,研究数据主要是大气可降水量(PWV)和细颗粒物(PM2.5)浓度指标,PWV值由国际GNSS服务组织(IGS)提供的位于北京房山的IGS观测站(BJFS站)的对流层产品反演计算得到,PM2.5数据则采用北京市环境保护监测中心网站(http://www.bjmemc.com.cn/)发布的北京市城市空气质量监测站的历史数据。为使相关性分析更为准确,本文选取与BJFS站较近的房山良乡空气质量监测站的PM2.5数据作为分析数据。
2.2 数据选取标准本文对北京市2014~2016年的城市空气质量进行研究分析,并绘制3 a的PM2.5时序变化图(图 1),同时统计每年4个季度对应AQI的6个等级(优、良、轻度污染、中度污染、重度污染、严重污染)的天数分布情况(图 2)。
|
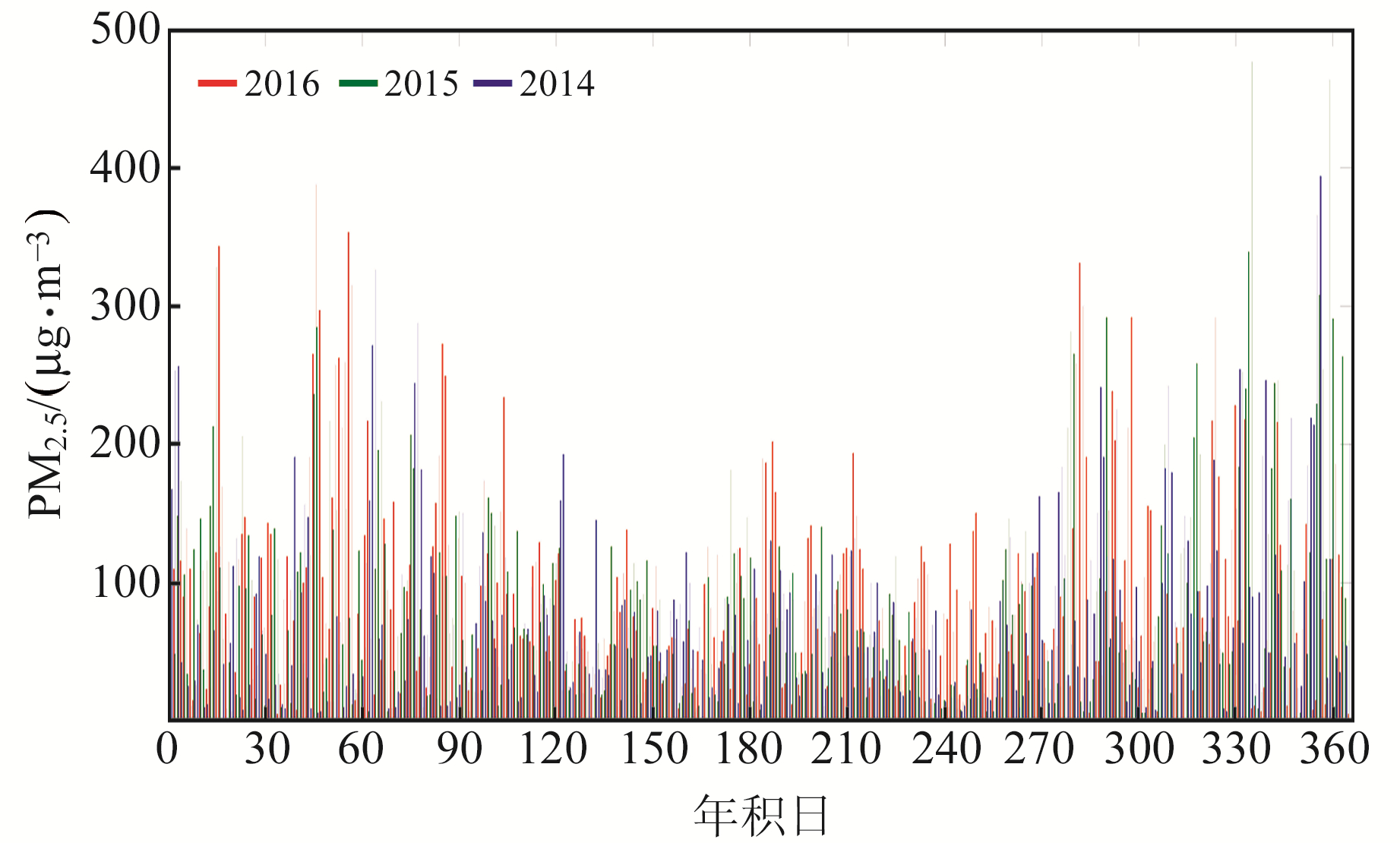
图 1 2014~2016年PM2.5时序变化 Fig. 1 Time series of PM2.5 from 2014 to 2016 |
|
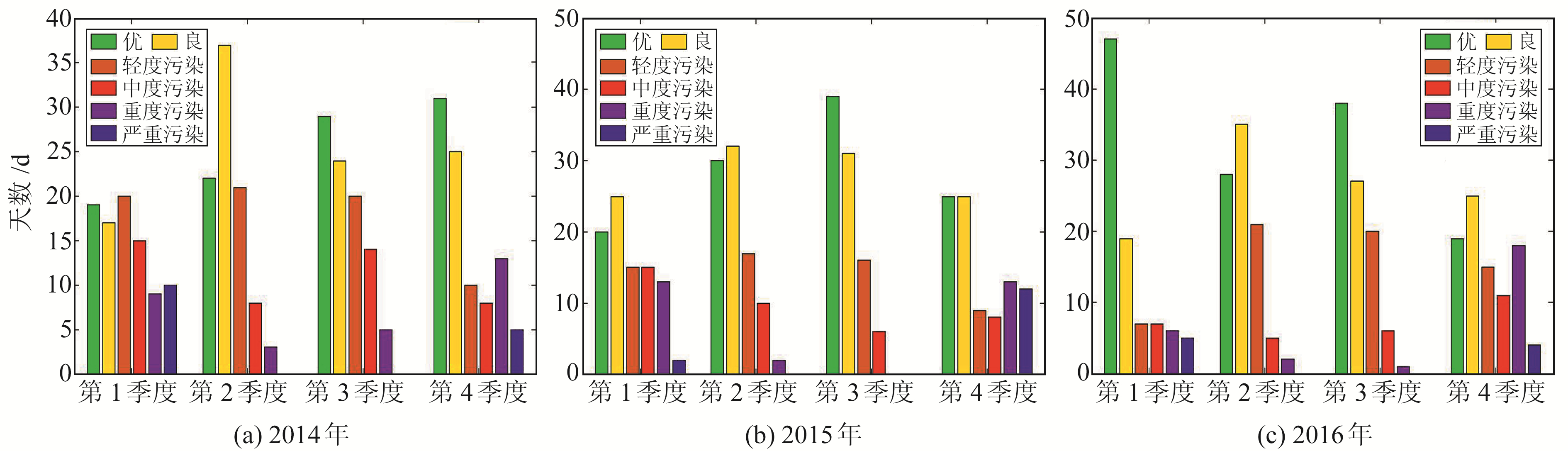
图 2 2014~2016年城市空气质量污染等级的季度分布 Fig. 2 Quarter distribution of urban air quality pollution level from 2014 to 2016 |
从图 1可以看出,2014~2016年PM2.5序列的变化趋势基本一致,表现出明显的周期性:年积日0~120的PM2.5变化较快,呈现出先增大后减小的变化趋势,且该时段PM2.5整体较高,最大值为2016年的393 μg/m3;年积日120~270的PM2.5变化相对平缓,具有连续的峰值但峰值较小,PM2.5整体较低;年积日270~366的PM2.5变化加快,具有多个峰值且峰值较大,PM2.5整体较高,最大值为2015年的476 μg/m3。由此可见,北京地区的PM2.5在年周期内呈现出“两边高、中间低”的变化特点,PM2.5在第1、4季度高、第2、3季度低,较大值分布在第1、4季度。
由图 2可知,3 a中AQI等级为严重污染的天气均分布在第1、4季度,第2、3季度均无严重污染天气,且轻度污染、中度污染、重度污染、严重污染4个等级对应的天气情况在第1、4季度明显多于第2、3季度。整体而言,第1、4季度的城市空气质量较第2、3季度的要差,第1、4季度更容易爆发严重的空气污染情况(雾霾天气)。造成该现象的原因主要是第1、4季度城市地表温度较低,空气密度较大,气压变化较为平稳,容易出现水平静风和垂直逆温现象,导致大量排放的污染物难以扩散而聚留在城市上空[22]。同时,该时段大气中的水汽含量较低,难以形成降雨,而空气中的水汽促进了污染物的二次转换,进一步增加了PM2.5的浓度[23]。本文定义上述时段为雾霾多发期,其他时段空气受雾霾污染的影响相对较少,定义为非雾霾多发期。
为避免大量非雾霾天气信息对PWV和PM2.5之间的相关性产生影响,本文仅选用雾霾多发期内的PWV与PM2.5数据作为分析对象,并由此引出数据选取的第1个标准——时间标准。由于雾霾多发期内仍存在非雾霾天气,为进一步将所选数据较集中地限制在雾霾天气内,本文提出数据选取的第2个标准——AQI等级标准。按表 1给出的AQI等级与PM2.5平均标准值之间的对应关系[24],选取雾霾多发期内AQI等级为严重污染、重度污染、中度污染、轻度污染对应时段的数据进行后续的相关性分析。
|
|
表 1 AQI等级与PM2.5平均标准值的对应关系 Tab. 1 Correspondence between air quality index and PM2.5 mean value |
本文相关性研究中PWV与PM2.5数据集中在2014~2016年雾霾多发期且AQI等级为严重污染、重度污染、中度污染、轻度污染4个等级的对应时段,时间分辨率为1 h。剔除少量异常值(如PWV数值较高而对应的PM2.5较低,如降雨天气)的数据,在保证数据质量的前提下经过筛选得到2014~2016年共4 831组PWV与PM2.5数据样本。由于基于2个选取标准下得到的数据并非等距连续,且数据类型和相关形式未知,考虑Pearson积矩相关系数的局限性,本文引入一种非参数性质的Spearman秩相关系数,其计算公式为:
| $ \rho=\frac{\sum\limits_{i=1}^{n}\left(R_{i}-\bar{R}\right)\left(S_{i}-\bar{S}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(R_{i}-\bar{R}\right)^{2} \sum\limits_{i=1}^{n}\left(S_{i}-\bar{S}\right)^{2}}} $ | (3) |
式中,Ri、Si分别为变量在各自顺序排列样本中所占位置的次序(即秩),R、S为Ri、Si的均值,n为样本个数。因为变量的秩不会被变量的任何严格单调递增变换所改变,所以Spearman秩相关系数对原始数据的分布类型、相关形式、数据选取没有严格限制,其通用性及稳健性均优于参数性质的Pearson积矩相关系数[6]。将筛选后的PWV与PM2.5数据作为研究对象,计算Spearman秩相关系数并进行相关性分析,数据处理方案见图 3。

|
图 3 数据处理方案示意图 Fig. 3 Schematic diagram of data processing |
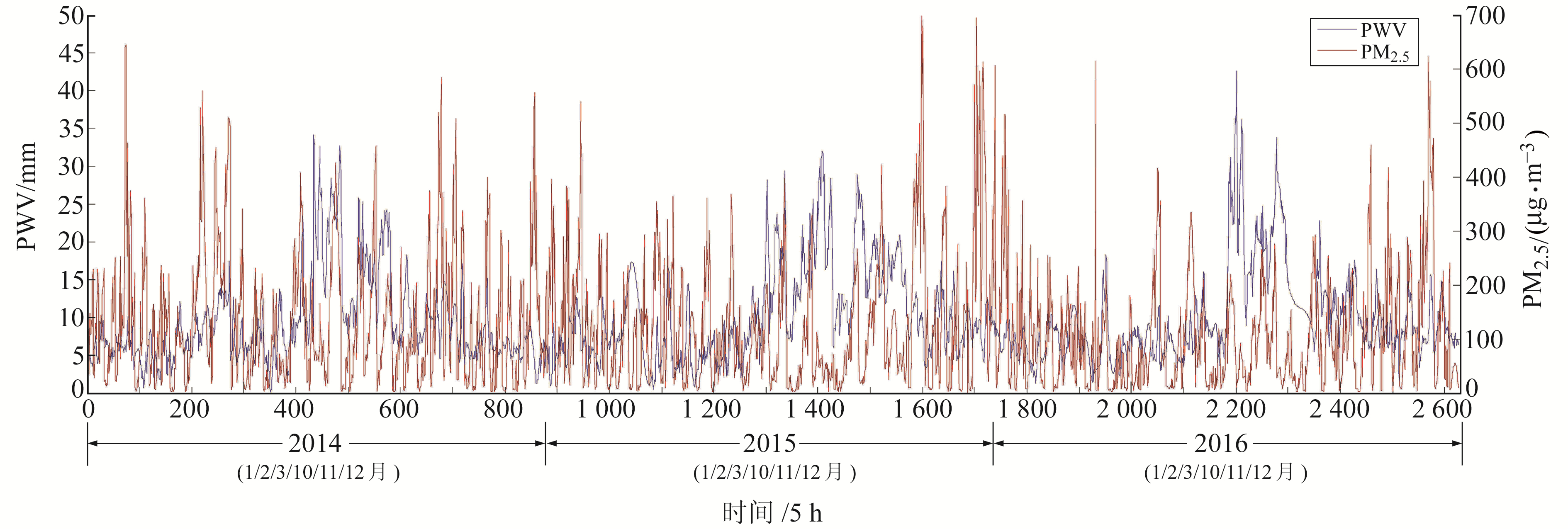
首先对北京市2014~2016年中第1季度和第4季度未筛选的PWV及PM2.5序列绘制时序变化图,并采用传统的相关性分析方法计算两者的Pearson积矩相关系数。由于PWV与PM2.5在某些时段存在数据缺失的情况,为满足Pearson积矩相关系数的计算条件(数据连续等距),按5 h的时间间隔采样得到时序变化图(图 4),其中2014~2016年的样本组数分别为874组、874组、878组。
|
图 4 北京市2014~2016年间PWV与PM2.5数据的时序变化 Fig. 4 Time series of PWV and PM2.5 data in Beijing from 2014 to 2016 |
考虑到传统分析方法所选的数据含有大量非雾霾天气的PWV与PM2.5,对选取的PWV与PM2.5数据样本直接绘制变化对比图(图 5),并计算Spearman秩相关系数,其中2014~2016年的样本组数分别为1 935组、1 498组、1 398组。

|
图 5 北京市2014~2016年间PWV与PM2.5数据的变化对比 Fig. 5 Comparison of PWV and PM2.5 data in Beijing from 2014 to 2016 |
可以看出,图 4中未经筛选的PWV序列整体上大致呈现出每年的第1季度逐渐增大、第4季度逐渐减小的周期性变化特点,PM2.5的变化则较为杂乱,两者的变化趋势差异较大,直观上难以看出相关关系。相比之下,图 5中筛选后的PWV与PM2.5的变化趋势整体上呈现出较好的一致性,PWV的增减与PM2.5的增减相对应,仅少许时段存在偏差。由每年的PWV与PM2.5变化还可以看出,2014年两者的变化一致性较2015年和2016年要好,每年第1季度的变化一致性较第4季度要好。由图 5可直观地看出PWV与PM2.5之间存在单调一致的相关性变化规律。
为定量分析未筛选和筛选后两者相关性的变化,对图 4和5中每年的第1、4季度数据分别计算Pearson积矩相关系数及Spearman秩相关系数,结果见表 2。
|
|
表 2 2014~2016年PWV与PM2.5相关系数统计 Tab. 2 Correlation coefficients between PWV and PM2.5 from 2014 to 2016 |
由表 2可知,数据未筛选时每年第1、4季度的γ值和ρ值均较小,PWV与PM2.5无明显相关特征;而数据筛选后的ρ值明显增大,且第1季度的ρ值大于第4季度,3 a中ρ值的均值在第1、4季度分别为0.661 3、0.628 0,整体均值为0.644 7,表明数据筛选后PWV与PM2.5呈现出单调正相关性,且第1季度的相关性大于第4季度,该结论与图 5的分析结果一致。
数据筛选的标准本质上是去除非雾霾天气的PWV与PM2.5,仅计算雾霾天气下两者的相关性。与未筛选的分析结果相比,筛选后PWV与PM2.5呈现出单调增加的相关性,表明非雾霾天气会对PWV与PM2.5的相关性认知产生影响,需要剔除非雾霾天气才能使分析结果更为准确和可靠。由此可见,雾霾天气下PWV与PM2.5之间存在较强的单调正相关性,其变化可相互影响,该结论为一些雾霾的成因解释[23, 25-26]提供了参考,表明水汽与雾霾的形成密切相关。
4 结语本文结合北京市2014~2016年城市空气质量的研究分析结果,提出2个可准确分析PWV与PM2.5相关性的数据选取标准——时间标准和AQI等级标准,将所选数据限制在雾霾天气下,能有效提高PWV与PM2.5相关性分析的针对性和可靠性。同时,为避免筛选后不连续数据受Pearson积矩相关系数局限性的影响,引入一种非参数性质的Spearman秩相关系数,通过对2014~2016年PWV与PM2.5的相关性进行统计,并与未筛选时的相关性分析结果进行比较,得出以下结论:1)数据未筛选时2种相关系数均较小,PWV与PM2.5无相关特征;2)筛选后3 a的Spearman秩相关系数在第1、4季度的均值分别为0.661 3、0.628 0,整体均值为0.644 7,表明雾霾天气下PWV与PM2.5之间存在较强的单调正相关性,且非雾霾天气会对两者的相关性认知造成影响;3)每年第1季度PWV与PM2.5的相关性强于第4季度。以上结论为探讨城市雾霾中挥发性和半挥发性物质等与水汽相关成分和大气水汽间的变化关系奠定了基础,对雾霾成因的解释具有重要的参考价值,拓宽了卫星导航定位技术在探索灾害性天气成因方面的应用。
| [1] |
Tai A P K, Mickley L J, Jacob D J. Correlations between Fine Particulate Matter(PM2.5) and Meteorological Variables in the United States: Implications for the Sensitivity of PM2.5 to Climate Change[J]. Atmospheric Environment, 2010, 44(32): 3 976-3 984 DOI:10.1016/j.atmosenv.2010.06.060
(  0) 0) |
| [2] |
Boersma K F, Jacob D J, Trainic M, et al. Validation of Urban NO2 Concentrations and Their Diurnal and Seasonal Variations Observed from the SCIAMACHY and OMI Sensors Using in Situ Surface Measurements in Israeli Cities[J]. Atmospheric Chemistry and Physics, 2009, 9(12): 3 867-3 879 DOI:10.5194/acp-9-3867-2009
(  0) 0) |
| [3] |
王勇, 闻德保, 刘严萍, 等. 雾霾天气对GPS天顶对流层延迟与可降水量影响研究[J]. 大地测量与地球动力学, 2014, 34(2): 120-123 (Wang Yong, Wen Debao, Liu Yanping, et al. Effects of Fog and Haze Weather on GPS Zenith Tropospheric Delay and Precipitable Water Vapor[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 120-123)
(  0) 0) |
| [4] |
王勇, 刘严萍, 李江波, 等. 不同季节的北京市GPS可降水量与PM2.5/PM10的比较研究[J]. 大地测量与地球动力学, 2015, 35(3): 365-367 (Wang Yong, Liu Yanping, Li Jiangbo, et al. The Comparison between GPS PWV and PM2.5/PM10 in Beijing on Different Seasons[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 365-367)
(  0) 0) |
| [5] |
王勇, 刘严萍. 基于小波分析的GPS PWV与PM2.5比较研究[J]. 大地测量与地球动力学, 2016, 36(5): 430-433 (Wang Yong, Liu Yanping. The Comparison between GPS PWV and PM2.5 Based on Wavelet Analysis[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 430-433)
(  0) 0) |
| [6] |
李裕奇, 赵联文, 王沁, 等. 非参数统计方法[M]. 成都: 西南交通大学出版社, 2010 (Li Yuqi, Zhao Lianwen, Wang Qin, et al. Nonparametric Statistical Methods[M]. Chengdu: Southwest Jiaotong University Press, 2010)
(  0) 0) |
| [7] |
Headrick T C. A Note on the Relationship between the Pearson Product-Moment and the Spearman Rank-Based Coefficients of Correlation[J]. Open Journal of Statistics, 2016, 6(6): 1 025-1 027 DOI:10.4236/ojs.2016.66082
(  0) 0) |
| [8] |
Hauke J, Kossowski T. Comparison of Values of Pearson's and Spearman's Correlation Coefficients on the Same Sets of Data[J]. Quaestiones Geographicae, 2011, 30(2): 87-93 DOI:10.2478/v10117-011-0021-1
(  0) 0) |
| [9] |
姚宜斌, 张顺, 孔建. GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1 408-1 420 (Yao Yibin, Zhang Shun, Kong Jian. Research Progress and Prospect of GNSS Space Environment Science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1 408-1 420)
(  0) 0) |
| [10] |
Rocken C, Ware R, Hove T V, et al. Sensing Atmospheric Water Vapor with the Global Positioning System[J]. Geophysical Research Letters, 2013, 20(23): 2 631-2 634
(  0) 0) |
| [11] |
Yuan L L, Anthes R A, Ware R H, et al. Sensing Climate Change Using the Global Positioning System[J]. Journal of Geophysical Research Atmospheres, 1993, 98(D8): 14 925-14 937 DOI:10.1029/93JD00948
(  0) 0) |
| [12] |
Duan J P, Bevis M, Fang P, et al. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water[J]. Journal of Applied Meteorology, 1996, 35(6): 830-838 DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2
(  0) 0) |
| [13] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [14] |
Ding M H. A Neural Network Model for Predicting Weighted Mean Temperature[J]. Journal of Geodesy, 2018, 92(10): 1 187-1 198 DOI:10.1007/s00190-018-1114-6
(  0) 0) |
| [15] |
Yao Y B, Xu C Q, Zhang B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2018, 197(1): 202-212
(  0) 0) |
| [16] |
Yao Y B, Sun Z Y, Xu C Q, et al. Extending a Model for Water Vapor Sounding by Ground-Based GNSS in Thevertical Direction[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2018, 179: 358-366 DOI:10.1016/j.jastp.2018.08.016
(  0) 0) |
| [17] |
叶世榕, 张双成, 刘经南. 精密单点定位方法估计对流层延迟精度分析[J]. 武汉大学学报:信息科学版, 2008, 33(8): 788-791 (Ye Shirong, Zhang Shuangcheng, Liu Jingnan. Precision Analysis of Precise Point Positioning Based Tropospheric Delay Estimation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 788-791)
(  0) 0) |
| [18] |
朱庆林, 赵振维, 吴振森. 精密单点定位方法测量对流层天顶延迟的精度改善[J]. 武汉大学学报:信息科学版, 2009, 34(9): 1 098-1 101 (Zhu Qinglin, Zhao Zhenwei, Wu Zhensen. Precision Improvemen of Tropospheric Zenith Path Delay Estimation by Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 098-1 101)
(  0) 0) |
| [19] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4 487-4 499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [20] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1972, 105(1): 279-298 DOI:10.1007/BF02521844
(  0) 0) |
| [21] |
Black H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research Solid Earth, 1978, 83(B4): 1 825-1 828 DOI:10.1029/JB083iB04p01825
(  0) 0) |
| [22] |
Zhou J K. Analysis of Causes and Hazards of China's Frequent Hazy Weather[J]. Open Cybernetics and Systemics Journal, 2015, 9(1): 1 311-1 314 DOI:10.2174/1874110X01509011311
(  0) 0) |
| [23] |
Wu Z J, Chen J, Wang Y, et al. Interactions between Water Vapor and Atmospheric Aerosols Have Key Roles in Air Quality and Climate Change[J]. National Science Review, 2018, 5(4): 452-454 DOI:10.1093/nsr/nwy063
(  0) 0) |
| [24] |
环境保护部科技标准司.HJ 633-2012环境空气质量指数(AQI)技术规定(试行)[S].北京: 中国环境科学出版社, 2012 (Department of Science and Technology Standards, Ministry of Environmental Protection. HJ 633-2012 Technical Regulation on Ambient Air Quality Index (on Trial)[S]. Beijing: China Environmental Science Press, 2012)
(  0) 0) |
| [25] |
Gui K, Che H Z, Chen Q L, et al. Aerosol Optical Properties Based on Ground and Satellite Retrievals during a Serious Haze Episode in December 2015 over Beijing[J]. Atmosphere, 2016, 7(5): 70 DOI:10.3390/atmos7050070
(  0) 0) |
| [26] |
韩艳妮, 王格慧. 华北农村大气PM2.5中水溶性物质化学组成、吸湿性能及光学特征[J]. 地球环境学报, 2016, 7(1): 48-58 (Han Yanni, Wang Gehui. Composition, Hygroscopicity and Light Absorption of Water-Soluble Fraction of PM2.5 at a Rural Site near Beijing[J]. Journal of Earth Environment, 2016, 7(1): 48-58)
(  0) 0) |
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, West High-Tec Zone, Chengdu 611756, China
 2020, Vol. 40
2020, Vol. 40


