2. 中国科学院上海天文台,上海市南丹路80号,200030
在全球定位导航系统(GNSS)和甚长基线干涉测量(VLBI)等空间大地测量应用中,精确的对流层延迟模型具有重要作用。VLBI数据处理分为实时模式和事后解算模式,在VLBI实时模式中,常用并址GNSS站点解算的多年ZTD序列进行拟合获取经验值,从而提供对应站点上的对流层延迟预报值。常用于计算实时对流层延迟的经验对流层延迟模型分为气象参数模型和经验改正模型,目前常用的气象参数模型天顶方向总延迟的改正精度可达cm级[1]。近年来,基于数值化气象模型的发展已建立多种较高精度的天顶延迟经验模型、映射函数经验模型以及对流层总延迟经验模型,提供了利用经验模型实时改正对流层延迟的可能性。
针对单站点天顶对流层延迟模型建模主要有3种思路:1)利用GPS解算的ZTD序列直接拟合模型,如在中国地区VLBI站点,针对各站点情况建立单站的本地化修正模型,对单个站点进行对流层延迟修正。2)利用欧洲中尺度气象数据分析中心(ECMWF)提供的气象格网数据建模,经高程改正后再利用经验公式计算ZTD,如Böhm等[2-3]基于IGS提供的GPS数据、ECMWF提供的气象数据以及VLBI的解算数据建立了GPT2、GPT2w等系列模型。3)利用ECMWF提供的气象格网数据积分ZTD,拟合模型参数并建立高程改正模型,如中国地区的对流层天顶延迟模型SHAO-C[4]、全球实时对流层天顶延迟改正模型SHAO-G[5],以及适用于任何高度的SHAO-H模型和进一步优化参数的SHAO-Gm模型。
为了改进经验对流层模型在中国地区VLBI站点的实时对流层延迟修正效果,本文根据思路1)将ZTD数据拟合为Local_ZTD模型;结合思路2)和思路3)将新一代ECWMF的ERA5格网气象数据改正到站点高度,再积分得到站点ZTD序列,拟合为Local_ERA模型。对比上述2种模型和目前常用的天顶对流层延迟经验模型GPT2w [6]、SHAO-Gm,利用VLBI站并址IGS数据评估这些模型用于中国地区VLBI实时对流层延迟改正的效果。
1 ERA5积分ZTD精度检验ERA5是基于上一代ERA-Interim的新一代数值气象资料集,同化了更多卫星数据和其他辅助测量数据,空间分辨率最高可达0.125°×0.125°,时间分辨率提高至1 h,气压层数据为0.001~1 000 hPa(共分为60层)。
由于对流层顶层湿延迟近似为0,所以顶层ZTD直接用Saastamoinen干延迟经验公式计算,其他各气压层ZTD用Saastamoinen总经验公式计算[7],再对各气压层格网数据进行积分:
| $ \mathrm{ZTD}_{\text {level }}=10^{-6} \int_{\text {surface }}^{\text {top }} N \mathrm{d} h $ | (1) |
N为大气折射指数,计算公式为:
| $ N=\frac{K_{1}(P-e)}{T}+\frac{K_{2} e}{T}+\frac{K_{3} e}{T^{2}} $ | (2) |
| $ e=\frac{q P}{0.622} $ | (3) |
式中,K1、K2、K3均为大气折射常数,分别为77.604 K/hPa、64.79 K/hPa、377 600 K2/hPa;P为每层对应气压(单位hPa),e为水汽压(单位hPa),T为温度(单位K),q为比湿[7]。从地表积分到气压层顶层后,再根据测站和地表高度差对气象数据进行高程改正[8]:
| $ P=P_{0}\left[1-\left(\frac{8.419 \times 10^{-5}\left(H-H_{0}\right)}{P_{0}^{0.190284}}\right)\right] $ | (4) |
| $ T=T_{0}-6.5\left(H-H_{0}\right) $ | (5) |
式中,P、T、H分别为测站气压、温度、高度,P0、T0、H0分别为地表的气压、温度、高度,单位分别为hPa、K、km。气象参数改正到测站高度后再根据式(1),由地表处高度积分ZTD改正到站点处ZTD。
对比2002~2017年全球VLBI服务组织(IVS)和对应IGS的ZTD序列,北京站(BJ)、上海站(SH)、乌鲁木齐站(UR)、昆明站(KM)4个站点mean bias为2.75 mm,mean RMS为7.983 mm。而对流层经验模型精度均在cm级,并且IGS测站上ZTD序列连续性更好,所以利用并址IGS站点的ZTD序列对不同分辨率的ERA5格网数据计算的ZTD进行精度检验,结果见表 1。
|
|
表 1 ERA5数据积分ZTD精度对比 Tab. 1 Resolution comparison of integrating ZTD of ERA5 data |
表 1中ERA_0.25表示由2010~2012年时间分辨率为6 h、空间分辨率为0.25°×0.25°的ERA5格网数据按照上述流程积分计算的ZTD,ERA_0.125表示由2010~2012年时间分辨率为1 h、空间分辨率为0.125°×0.125°的ERA5格网数据按照上述流程积分计算的ZTD。
如表 1所示,各站点上都有一定的系统性偏差,如上海站偏差值为负值,说明ERA5积分计算的ZTD偏小。空间分辨率越高,单个站点平均偏差越接近于0,说明格网空间分辨率越高,格网积分计算ZTD的系统性偏差越小。使用的气压层数据积分空间分辨率越高,平均RMS越小,平均精度越高,如分辨率为0.125°格网相比0.25°格网平均偏差减少25.14%,平均RMS减少32.28%。
2 本地化经验模型改进GPT2w模型拟合参数为气象数据,使用时根据测站坐标和时间点获得水准面上的气象数据,将气象数据高度改正到对应IGS站点高度,再利用测站气象数据和经验模型[9-10]计算对应测站ZTD。SHAO-Gm[11]模型拟合参数过程不涉及气象数据,使用时直接根据测站坐标和时间点获得测站水准面ZTD,再根据测站与水准面高差利用高差模型进行改正。
由于国内VLBI站点较少,考虑利用单个站点本地数据建立针对单个站点ZTD的本地化模型。由于单站点建模不需要积分计算ZTD到统一水准面再针对站点高度进行改正,而是直接进行高度改正获得测站气象参数,再积分获得测站ZTD,所以本地化模型直接针对ZTD序列建模而不涉及具体气象参数。
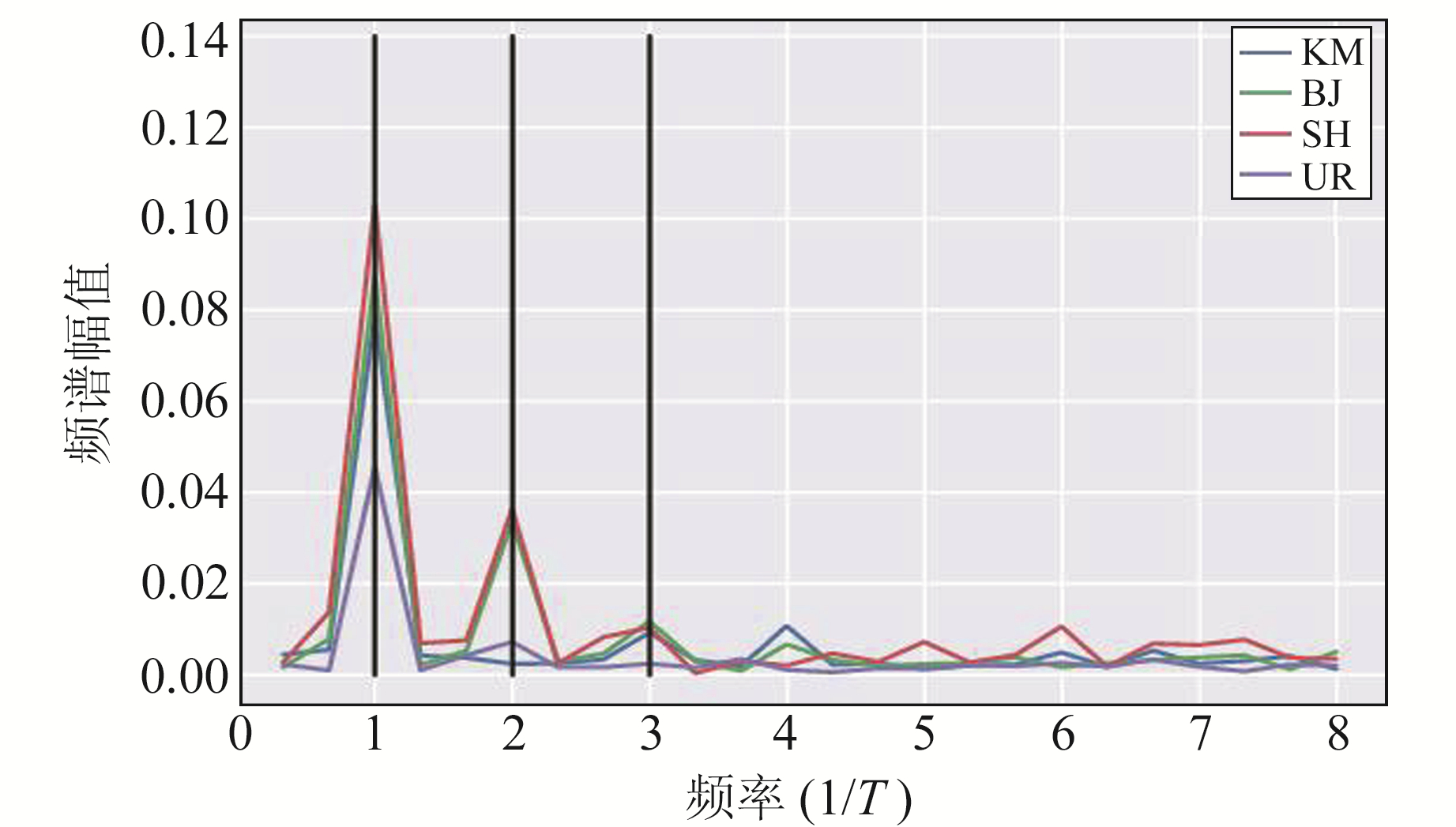
对4个站点多年的ZTD资料(2004~2012年)剔除粗差后插值补全,再进行快速傅里叶频谱分析(FFT),根据频率部分截断后如图 1所示,横轴表示频率即1/T,T取为年周期信号,纵轴为FFT转换后的信号频谱幅值。从图中可以看出,多年ZTD信号震荡周期主要分布在T、T/2、T/3处,因此拟合表达式中三角函数周期信号表达如式(6),除了考虑年周期、半年周期,还加入了T/3的季节性周期表达。
|
图 1 4个站点ZTD信号的FFT频谱分析(2001~2010年) Fig. 1 FFT spectrum analysis of ZTD signal of four stations (2001~2010) |
利用2010~2012年4个VLBI站的ZTD序列,采用式(6)的三角函数表达式表达周期性信号:
| $ \begin{array}{c} r(t)=A_{0}+A_{1} \cos \left(\frac{\text { hoy }}{365.25 \times 24} 2 \pi\right)+ \\ B_{1} \sin \left(\frac{\text { hoy }}{365.25 \times 24} 2 \pi\right)+A_{2} \cos \left(\frac{\text { hoy }}{365.25 \times 24} 4 \pi\right)+ \\ B_{2} \sin \left(\frac{\text { hoy }}{365.25 \times 24} 4 \pi\right)+A_{3} \cos \left(\frac{\text { hoy }}{365.25 \times 24} 6 \pi\right)+ \\ B_{3} \sin \left(\frac{\text { hoy }}{365.25 \times 24} 6 \pi\right) \end{array} $ | (6) |
式中,Ai、Bi为针对单个站点的拟合常数,使用时只需要根据测站确定对应Ai、Bi参数和对应时间点hoy。式(6)的最后2项为T/3的季节性周期项,拟合参数Ai、Bi时输入的原始数据时间分辨率由6 h提高为1 h。基于2010~2012年4个站点上每小时的ZTD序列直接按照上述方法拟合为Local-ZTD模型。基于高精度ERA5格网数据(时间分辨率为1 h,空间分辨率为0.125°×0.125°)积分测站ZTD序列按照上述方法拟合为Local_ERA模型。
对比之前VLBI站点上实时处理使用的本地化模型,改进后的本地化模型拟合过程中加入了半年周期项和季节性周期项,同时更新了ZTD的数据来源,并加入了ERA5格网积分的ZTD数据。基于2013年IGS的ZTD数据对比(时间分辨率为6 h),改进后Local-ERA模型比原有模型平均RMS减少13.411%,改进后的Local-ZTD模型比原有模型平均RMS减少12.738%。
3 基于IGS数据的各模型对比为了验证利用2010~2012年资料拟合的本地模型的预报精度,利用2013~2014年VLBI站并址的IGS站点ZTD数据,对4种经验模型进行对比(IGS提供的站点ZTD剔除粗差后精度可达1~4 mm),4种模型的参数说明如表 2所示。
|
|
表 2 经验模型对比 Tab. 2 Comparison of empirical models |
模型精度统计时,采用bias绝对值和RMS指标:
| $ \begin{aligned} &\text { bias }=\frac{1}{N} \sum\limits_{i=1}^{N}\left| \mathrm{ZTD}_{\text {model }, i}- \mathrm{ZTD}_{\mathrm{IGS}, i}\right|\\ &\mathrm{RMS}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left( \mathrm{ZTD}_{\text {model }, i}- \mathrm{ZTD}_{\mathrm{IGS}, i}\right)^{2}} \end{aligned} $ | (7) |
模型精度统计结果如表 3(单位cm)所示,其中由于昆明站缺失2013~2014年IGS ZTD数据,本文选取2008~2009年期间数据进行对比。从表中可以看出,4个经验模型计算ZTD的平均精度都在3~4 cm,采用ZTD序列直接建立的Local_ZTD平均精度高于SHAO-Gm、GPT2w模型,利用高精度ERA5格网积分ZTD序列建模的Local_ERA模型精度与Local_ZTD接近,Local_ERA、Local_ZTD模型相比于SHAO-Gm模型平均精度提高约15%,相比GPT2w平均精度提高约7%。
|
|
表 3 经验模型精度对比 Tab. 3 Accuracy comparison of empirical models |
图 2说明,4种经验模型变化总体具有一致性,其中Local_ZTD模型和Local_ERA模型精度相近,相对于现有的经验模型GPT2w、SHAO-Gm系列均有一定的改进。

|
图 2 4个站点上经验模型精度的对比(基于2013~2014年IGS数据) Fig. 2 Accuracy comparison of empirical models based on IGS in four VLBI sites in 2013~2014 |
针对站点分布情况,考虑季节性周期后的Local_ZTD、Local_ERA本地经验模型在各个站点的精度均比SHAO-Gm、GPT2w模型有所提高,图 2(a)BJ站季节性周期较明显。其中本地经验模型Local_ERA平均RMS略小于Local_ZTD,相比于SHAO-Gm模型平均精度提高24.88%,相比GPT2w模型平均精度提高约20.53%。在图 2(a)~(c)中BJ站、SH站、UR站的绝对差值序列均在4~9月份偏大,而在10~次年3月份减小,说明只拟合年周期、半年周期和季节性变化的经验模型不能较好地反映水汽变化。结合图 1中FFT频谱分析结果,SH站的ZTD序列在T/5、T/6处仍然具有一定的周期性变化,KM站在T/4处也具有一定的周期性变化,因此考虑进一步优化拟合模型。
同时,图 2(a)、2(b)中BJ站、SH站水汽随机性变化较大,绝对偏差值较大,而图 2(c)中水汽较少的UR站绝对偏差值较小,并且Local_ERA相比于SHAO-Gm模型平均精度提高约22.95%,说明站点水汽越大,周期性模型经验值的偏差值可能越大,可以考虑结合短期预报随机模型进行ZTD精确预报。同时如图 2(a)、2(c)所示,在BJ站和UR站,GPT2w模型获得的ZTD相比于对应IGS提供的ZTD数据整体偏小。改进后的模型在VLBI大地测量技术中,能够提供对流层延迟经验值,为定位提供更精确的对流层先验值或直接运用于实时性修正。本文基于IVS以及IGS提供的ZTD数据对优化后的本地化模型在VLBI站点上进行了精度检验,下一步将考虑优化后的模型在实际数据处理中的应用。
4 结语为了探索更适合中国地区天顶对流层延迟改正的模型,本文总结了常用的气象参数模型和经验模型。选取全球精化的格网经验气象模型GPT2w模型、直接针对ZTD时空变化特点建立的经验模型SHAO-Gm以及针对各个站点改进后的本地化经验模型Local_ERA和Local_ZTD模型以对应的IGS实测ZTD作为基准进行对比,获得以下结论:
1) 改进后的本地化模型Local_ERA和Local_ZTD在中国VLBI站点上均比现有常用经验模型SHAO-Gm、GPT2w精度有所提高,尤其在BJ站,平均RMS提高约20%。
2) 基于2种不同ZTD数据建立的本地化模型Local_ERA和Local_ZTD精度相当,说明当缺失GPS数据时可以利用高分辨率的ERA5格网数据积分计算ZTD,并建立对流层经验模型,获取对流层延迟经验值。
3) 本地化模型加入季节性周期项后,在水汽季节性变化较大的BJ站改进效果明显,但在水汽随机变化较大的SH站精度提高不明显。下一步将考虑模型水汽随机变化的影响,进一步优化模型。
| [1] |
Yao Y B, Peng W J, Xu C Q, et al. Enhancing Real-Time Precise Point Positioning with Zenith Troposphere Delay Products and the Determination of Corresponding Tropospheric Stochastic Models[J]. Geophysical Journal International, 2017, 208(2): 1 217-1 230 DOI:10.1093/gji/ggw451
(  0) 0) |
| [2] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [3] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [4] |
Song S L, Zhu W Y, Chen Q M, et al. Establishment of a New Tropospheric Delay Correction Model over China Area[J]. Science China:Physics, Mechanics and Astronomy, 2011, 54(12): 2 271-2 283 DOI:10.1007/s11433-011-4530-7
(  0) 0) |
| [5] |
陈钦明, 宋淑丽, 朱文耀.全球对流层延迟改正模型(SHAO-G)的初步建立[C].第二届中国卫星导航学术年会, 上海, 2011 (Chen Qinming, Song Shuli, Zhu Wenyao. Establishment of Tropospheric Delay Correction Model SHAO-G[C]. China Satellite Navigation Conference, Shanghai, 2011)
(  0) 0) |
| [6] |
Liu J Y, Chen X H, Sun J Z, et al. An analysis of GPT2/GPT2w+Saastamoinen Models for Estimating Zenith Tropospheric Delay over Asian Area[J]. Advances in Space Research, 2017, 59(3): 824-832 DOI:10.1016/j.asr.2016.09.019
(  0) 0) |
| [7] |
Chen Q M, Song S L, Heise S, et al. Assessment of ZTD Derived from ECMWF/NCEP Data with GPS ZTD over China[J]. GPS Solutions, 2011, 15(4): 415-425 DOI:10.1007/s10291-010-0200-x
(  0) 0) |
| [8] |
赵静旸, 宋淑丽, 朱文耀. ERA-Interim应用于中国地区地基GPS/PWV计算的精度评估[J]. 武汉大学学报:信息科学版, 2014, 39(8): 935-939 (Zhao Jingyang, Song Shuli, Zhu Wenyao. Accuracy Assessment of Applying ERA-Interim Reanalysis Data to Calculate Ground-Based GPS/PWV over China[J]. Geomatics and Information science of Wuhan University, 2014, 39(8): 935-939)
(  0) 0) |
| [9] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1972, 105(1): 279-298 DOI:10.1007/BF02521844
(  0) 0) |
| [10] |
Askne J, Nordius H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 1987, 22(3): 379-386 DOI:10.1029/RS022i003p00379
(  0) 0) |
| [11] |
赵静旸, 宋淑丽, 陈钦明, 等. 基于垂直剖面函数式的全球对流层天顶延迟模型的建立[J]. 地球物理学报, 2014, 57(10): 3 140-3 153 (Zhao Jingyang, Song Shuli, Chen Qinming, et al. Establishment of a New Global Model for Its Vertical Profile[J]. Chines Journal of Geophysics, 2014, 57(10): 3 140-3 153)
(  0) 0) |
2. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China
 2020, Vol. 40
2020, Vol. 40

