2. 中国地质大学(北京)信息工程学院,北京市学院路29号,100083
GNSS技术采用的坐标系统为地心坐标系统,其所测高程为大地高。由于工程实际中一般采用正常高,因此有必要将GNSS高程转换为正常高。
| $ H=h+ε $ | (1) |
式中,H为大地高,h为正常高,ε为高程异常。
由式(1)可知,GNSS高程拟合的关键在于准确求解高程异常值。目前求取高程异常值常用的方法有二次多项式曲线拟合、多面函数拟合、二次曲面拟合、神经网络法等[4-9]。由于人工神经网络具备强大的自学习与自适应能力,在数据拟合过程中能够自动化寻找数据间的内在关系等,国内外已有众多学者将其应用于GNSS高程拟合研究领域。
石长伟等[10]将RBF神经网络应用于区域性GNSS高程拟合研究发现,RBF神经网络在GNSS高程拟合中误差可控制在mm级,但其稳定性仍然较差,拟合残差最大值仍可达到cm级水平。彭中波等[11]将BP神经网络应用于水下高程拟合,解决了水下地形图高程测量施工难度大、操作复杂等问题,但其拟合精度相对较低。束蝉方等[12]基于RBF神经网络进行GNSS高程拟合,通过利用Delaunay三角分割等方法计算RBF神经网络基函数中心,输出权值等参数的较优值,但其拟合精度和稳定性仍然相对较差。高宁等[13]将RBF神经网络应用于矿区高程转换,通过对比分析发现,RBF神经网络拟合精度高于标准的BP、GA-BP算法,但其稳定性仍需改进。
本文针对传统的RBF神经网络模型在GNSS高程拟合中拟合精度低、稳定性较差、相关因子无法自动化确定等问题,提出一种改进的自适应权重粒子群算法,将其与MATLAB RBF神经网络函数newrb相结合,实现RBF神经网络函数模型隐含节点数和SPREAD的自动优化选取,提高RBF神经网络算法的拟合精度和稳定性。通过实例数据分析,该算法在GNSS高程拟合中精度得到提高,可达mm级,优于传统的二次多项式模型,且算法稳定性良好。
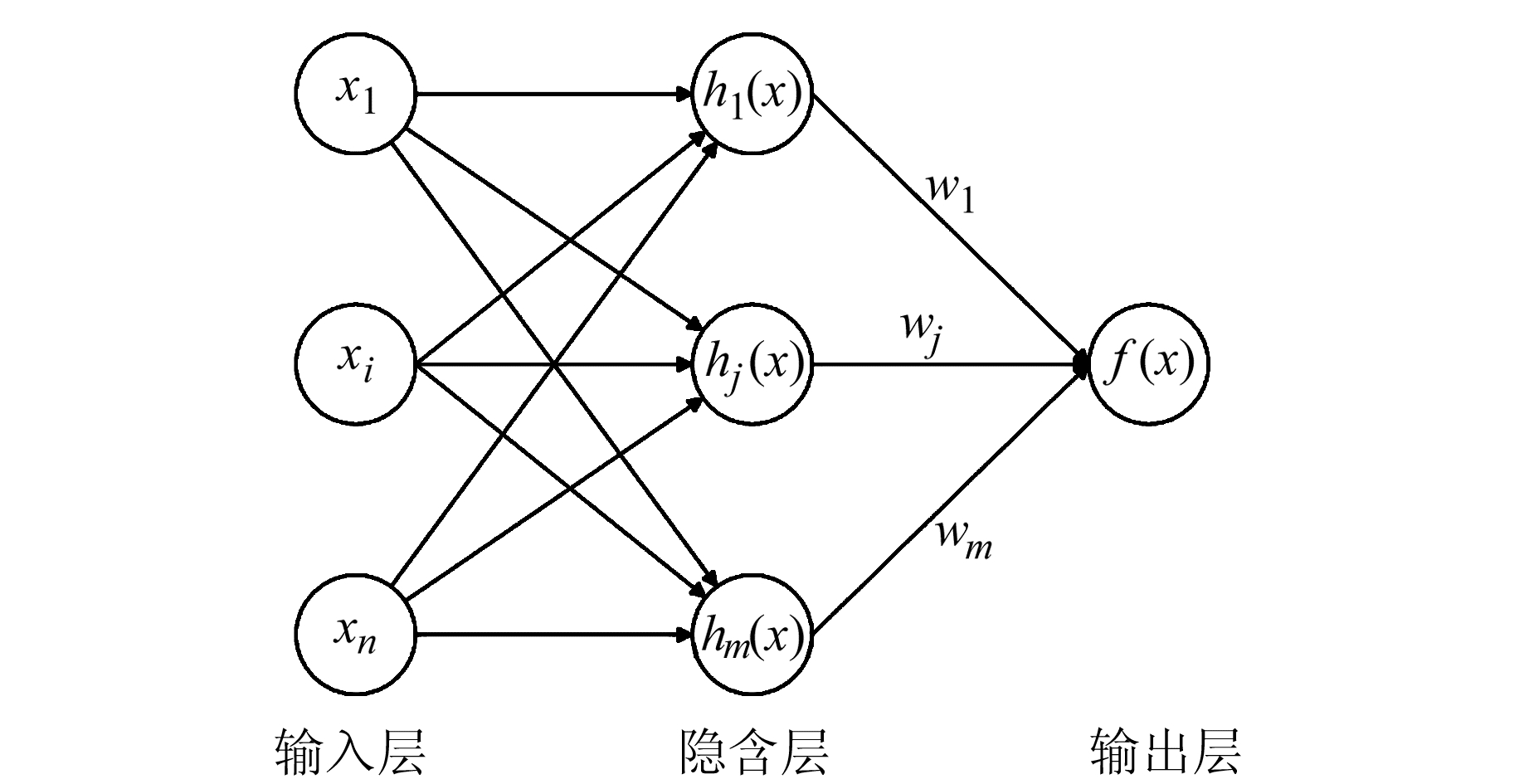
1 RBF神经网络高程拟合模型 1.1 RBF神经网络基本原理RBF神经网络是一种3层前向网络,第1层为输入层,第2层为隐含层,第3层为输出层。其基本思想是通过隐含层将输入矢量转换到高纬度空间中,实现低维度空间内线性不可分问题在高维度空间内线性可分(图 1)。RBF神经网络基本学习算法流程如下:
|
图 1 RBF神经网络拓扑结构 Fig. 1 Topological structure of RBF neural network |
1) 输入训练样本,获取网络聚类中心ci,求取方差δi(i=1, 2, …, m);
2) 基于径向基函数(高斯函数)求取隐含层输出值:
| $ h_{j}=\sum\limits_{i=1}^{n} \exp \left(-\frac{\left\|x_{i}-c_{j}\right\|^{2}}{2 \delta_{j}^{2}}\right) $ | (2) |
其中, j=1, 2, 3, …, m;
3) 求取输出权值:
| $ w_{j}=\exp \left(\frac{h}{c_{\max }}\left\|x_{p}-c_{i}\right\|^{2}\right) $ | (3) |
式中,j=1, 2, 3, …, m, p=1, 2, 3, …, P(P为样本数);
4) 求取网络输出值:
| $ f(x)=\sum\limits_{i=1}^{m} h_{i}(x) w_{i} $ | (4) |
基于RBF神经网络的GNSS高程拟合基本原理为:将已知点的坐标(x, y)作为网络的输入层,对应的高程异常值ε作为网络的输出层,并通过GNSS拟合数据建立RBF神经网络高程拟合模型;同时利用检验点数据验证模型精度。其基本流程如下。
1) GNSS拟合数据归一化处理;
2) 利用GNSS拟合数据建立RBF神经网络高程拟合模型;
3) 将检验点坐标(x, y)作为网络输入层,求取对应的高程异常值;同时,将外符合精度作为精度评价指标,确定模型拟合精度。
2 改进的RBF神经网络高程拟合模型在使用RBF神经网络进行数据拟合时,需要人为提前设置好相关参数因子。参数因子的设置将直接决定RBF神经网络拟合的精度和稳定性,且参数因子最优值随拟合数据的变化而发生相应改变。本文通对自适应权重粒子群算法的惯性权重进行改进,提高粒子群算法的优化能力;将该优化算法与MATLAB RBF神经网络函数newrb相结合,利用改进的粒子群算法良好的寻优能力,实现RBF神经网络newrb函数模型隐含节点数和SPREAD值的自动化优化设置,提高RBF神经网络GNSS高程拟合的精度和稳定性。
2.1 粒子群优化算法基本原理将待求解问题的每一个潜在解看作空间中的一个粒子,根据所要求解的问题,赋予每个粒子一个函数值F(适应度)与速度V,各粒子根据最优粒子位置和自身目前最优位置来不断更新自己的速度与位置, 从而求解问题的最优解。
假设求解问题为n维空间,有m个粒子参与运算,第i个粒子的位置为Xi(xi1, xi2, xi3, …, xin),其速度为Vi(vi1, vi2, vi3, …, vin)。速度与位置更新公式为:
| $ \begin{aligned} V_{i(d+1)}=& w \times v_{i d}+c_{1} r_{1}\left(P_{i d}-X_{i d}\right)+\\ & c_{2} r_{2}\left(P_{g d}-X_{i d}\right) \end{aligned} $ | (5) |
| $ X_{i(d+1)}=X_{i d}+r \times v_{i d} $ | (6) |
式中,Vid为第d次迭代时第i个粒子的速度,Xid为第d次迭代时第i个粒子的位置;c1、c2为算法的学习因子,取值为2;wmax=0.9、wmin=0.4为惯性权重最大值和最小值,w为惯性权重;Pid为粒子自身目前最优位置,Pgd为粒子群当前最优位置。
2.2 改进的自适应权重粒子群优化算法对于自适应权重粒子优化算法,其惯性权重更新策略为:首先求取粒子群平均适应度favg和最小适应度fmin, 对于适应度f大于平均适应度的粒子,其惯性权重更新公式为:
| $ w=w_{\min }+\left(f-f_{\min }\right) \frac{w_{\max }-w_{\min }}{f_{\operatorname{avg}}-f_{\min }} $ | (7) |
对于适应度大于平均适应度的粒子,令其惯性权重值为wmax。
黄洋等[14]提出基于S型函数的自适应粒子群优化算法,其惯性权重更新公式为:
| $ w = {w_{\max }} - \left( {{w_{\max }} - {w_{\min }}} \right)\frac{1}{{1 + {{\rm{e}}^{a - bt}}}} $ | (8) |
为了提高自适应权重粒子群算法后期局部搜索能力,保留其粒子分群等优点,提高求解精度,本文将式(8)引入到自适应权重粒子群算法中,对于适应度小于平均适应度的粒子其惯性权重采用式(7),大于平均适应度的粒子采用式(8)。位置更新公式采用文献[14]的公式。
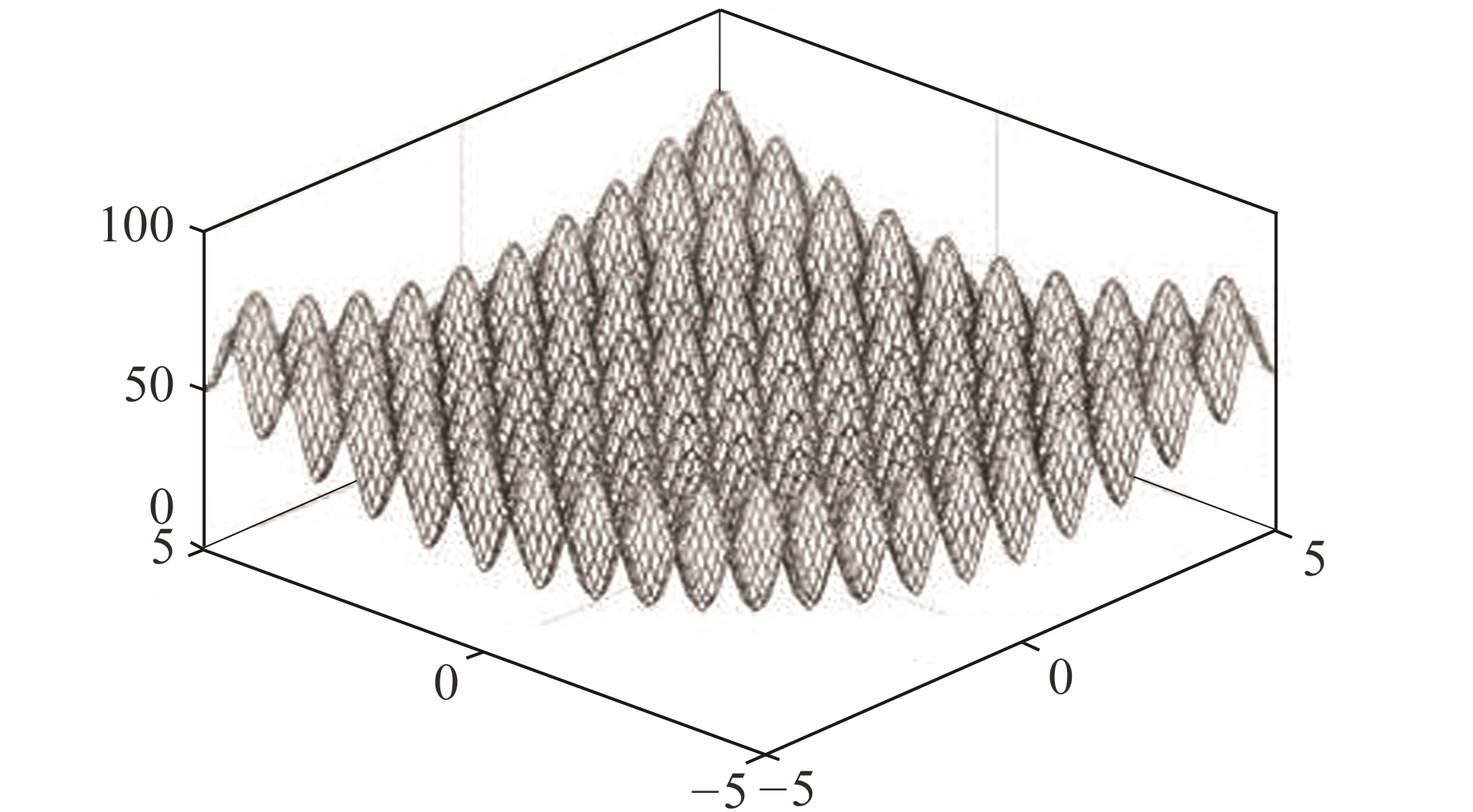
2.3 仿真实验分析为了验证本文提出的改进粒子群算法优化能力,采用函数fv=20+x2+y2-10(cos(2πx)+cos(2πy))进行20次仿真实验。该函数在区间[-5, 5;-5, 5]上具有多个极小值,在点(0, 0)处有最小值0。函数图像见图 2。
|
图 2 多峰值函数 Fig. 2 Multi-peak function |
分别利用基本粒子群算法、自适应权重粒子群算法以及本文改进的粒子群算法进行寻优计算,其结果为:基本粒子群算法精度最差,无法找到最小值;自适应权重粒子群算法精度较高,但仍会出现收敛局部解的情况;本文改进的粒子群优化算法精度最高,20次实验均能找到最优解(见表 1,(X, Y)为最优粒子平面位置,FV为相应函数值)。通过仿真实验可知,本文改进的自适应权重粒子群算法相对于传统的自适应权重粒子群算法,求解精度和稳定性提高了25%。
|
|
表 1 粒子群算法寻优情况 Tab. 1 Particle swarm optimization |
基于改进的RBF神经网络的GNSS高程拟合步骤如下:
1) 导入GNSS拟合数据,平面坐标(x, y)作为输入向量,高程异常值作为输出向量;
2) 利用MATLAB mapminmax函数将数据归一化处理;
3) 将训练数据代入RBF神经网络,利用改进的粒子群算法优化寻找RBF神经网络隐含节点数和SPREAD值,并根据优化选取的隐含节点数和SPREAD值,获取最终神经网络模型;
4) 将测试数据代入训练好的RBF神经网络模型,获取拟合值;同时,将外符合精度作为精度评价指标,确定模型拟合精度。
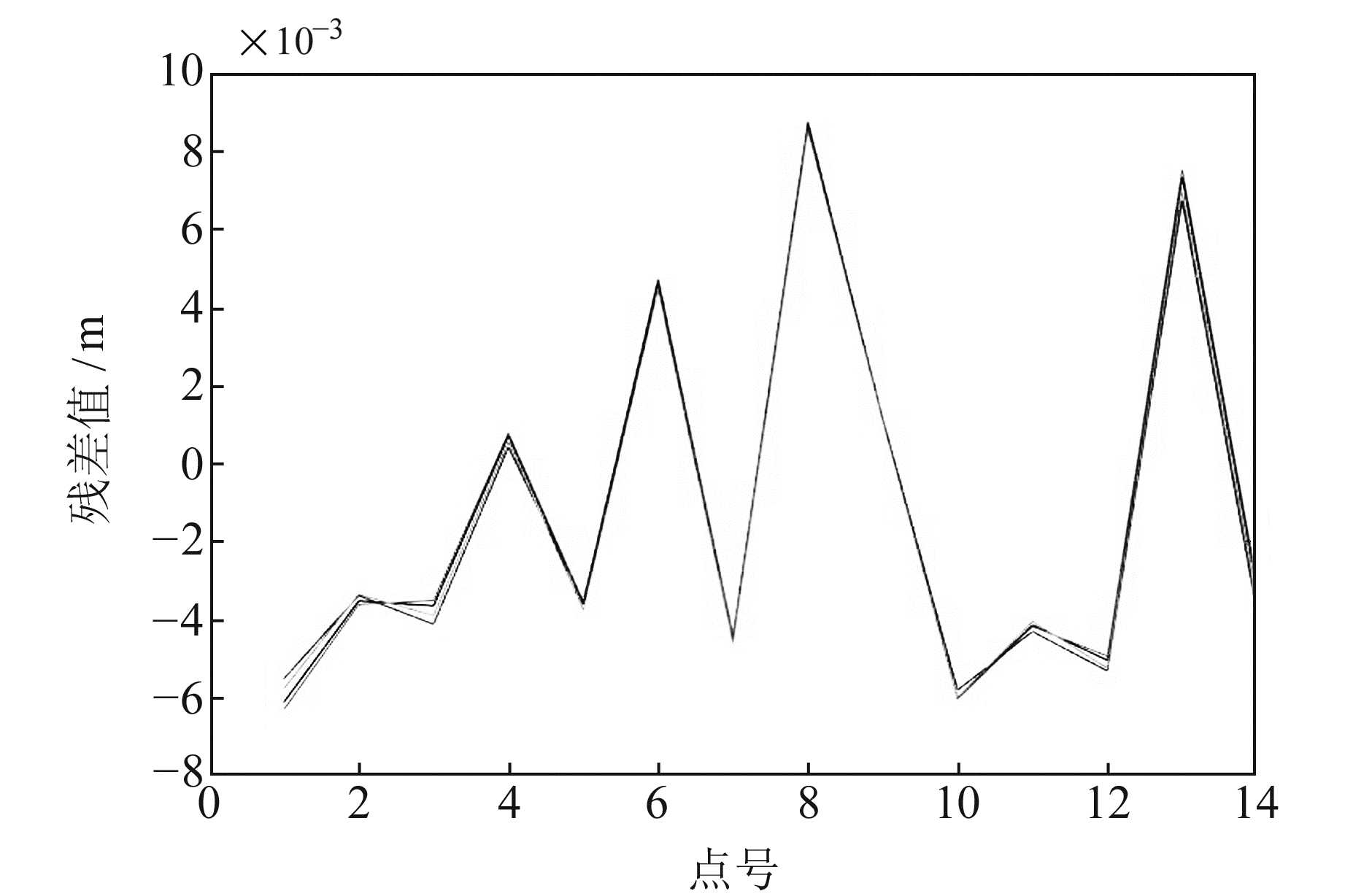
3 实验分析本文采用某市区中的40个经四等水准联测的GNSS控制点作为实验数据,其中前26个点作为训练样本数据,后14个点作为神经网络模型测试数据。首先利用改进的RBF神经网络模型进行10次GNSS高程拟合实验。其测试数据残差见图 3。
|
图 3 10次实验拟合残差值 Fig. 3 Fitting residual values of 10 experiments |
由图 3可知,改进的RBF神经网络GNSS高程拟合模型稳定性较高,每次各点残差值均能够控制在mm级,10次拟合实验结果十分稳定,波动性较小。
将测试数据的外符合精度作为最终精度评价指标,对本文改进的RBF神经网络模型与常规的RBF神经网络模型、二次多项式拟合模型进行精度对比分析(表 2)。通过精度分析可知,改进的RBF神经网络模型相对于传统的RBF神经网络模型精度提高73%,相对于二次多项式模型精度提高17%。
|
|
表 2 各模型的外符合精度 Tab. 2 External coincidence accuracy of each model |
本文通过利用改进的粒子群算法与MATLAB RBF神经网络函数模型newrb相结合,实现newrb函数中隐含节点数与SPREAD值的自动优化选取,提高了RBF神经网络模型在GNSS高程拟合过程中的稳定性和精度。通过实例数据分析可知,该算法拟合稳定性较高,各点残差值可控制在mm级,外符合精度可达到mm级,优于传统的二次多项式模型和传统的RBF神经网络模型,对于精确求解高程异常值具有重要的参考价值。
| [1] |
蒲伦, 唐诗华, 张紫萍, 等. 基于蚁群算法的多面函数在GPS高程拟合中的应用[J]. 大地测量与地球动力学, 2019, 39(1): 31-35 (Pu Lun, Tang Shihua, Zhang Ziping, et al. Application of Multi-Quadric Function Based on Ant Colony Algorithm in GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2019, 39(1): 31-35)
(  0) 0) |
| [2] |
刘建, 王琪洁, 王小辉, 等. 基于遗传算法的RBF神经网络在GPS高程拟合中的应用[J]. 测绘科学, 2013, 38(2): 143-145 (Liu Jian, Wang Qijie, Wang Xiaohui, et al. Application of RBF Neural Network to GPS Elevation Fitting Based on Genetic Algorithm[J]. Science of Surveying and Mapping, 2013, 38(2): 143-145)
(  0) 0) |
| [3] |
陈智伟, 张兴福, 胡波, 等. 利用RBF实现线状工程中GNSS高程转换的精度分析[J]. 测绘通报, 2018(12): 79-82 (Chen Zhiwei, Zhang Xingfu, Hu Bo, et al. Using RBF to Analyze the Accuracy of GNSS Height Transformation in Linear Engineering[J]. Bulletin of Surveying and Mapping, 2018(12): 79-82)
(  0) 0) |
| [4] |
方苏阳, 赵勇. GPS高程拟合方法对比研究分析[J]. 全球定位系统, 2018, 43(4): 110-116 (Fang Suyang, Zhao Yong. Experimental Research on GPS Height Fitting Method[J]. GNSS World of China, 2018, 43(4): 110-116)
(  0) 0) |
| [5] |
张海燕, 李秀海, 韩冰. 基于三次样条函数的长线路GNSS高程拟合研究[J]. 测绘工程, 2018, 27(7): 15-17 (Zhang Haiyan, Li Xiuhai, Han Bing. Research on GNSS Height Fitting for Long Line Area Based on Cubic Spline Function[J]. Engineering of Surveying and Mapping, 2018, 27(7): 15-17)
(  0) 0) |
| [6] |
Tao Y Q, Mao G X, Zhou X Z. Solution for GNSS Height Anomaly Fitting of Mining Area Based on Robust TLS[J]. Acta Geodaetica et Geophysica, 2018, 53(2): 295-307 DOI:10.1007/s40328-018-0217-0
(  0) 0) |
| [7] |
杨帆, 王小兵, 谢洋洋, 等. 灰色神经网络在GPS高程拟合中的应用[J]. 导航定位学报, 2017, 5(3): 90-93 (Yang Fan, Wang Xiaobing, Xie Yangyang, et al. Application of Grey Neural Network in GPS Height Fitting[J]. Journal of Navigation and Positioning, 2017, 5(3): 90-93 DOI:10.3969/j.issn.2095-4999.2017.03.018)
(  0) 0) |
| [8] |
魏宗海. 几种改进的BP神经网络在GPS高程拟合中的应用比较[J]. 全球定位系统, 2016, 41(5): 99-103 (Wei Zonghai. Comparison of Several Improved BP Neural Network in GPS Height Fitting[J]. GNSS World of China, 2016, 41(5): 99-103)
(  0) 0) |
| [9] |
刘斌, 郭际明, 史俊波, 等. 利用EGM2008模型与地形改正进行GPS高程拟合[J]. 武汉大学学报:信息科学版, 2016, 41(4): 554-558 (Liu Bin, Guo Jiming, Shi Junbo, et al. A GPS Height Fitting Method Based on the EGM2008 Model and Terrain Correction[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 554-558)
(  0) 0) |
| [10] |
石长伟, 何晴晴, 陈长坤. RBF神经网络在区域性GPS高程拟合中的应用与精度分析[J]. 测绘与空间地理信息, 2018, 41(11): 94-96 (Shi Changwei, He Qingqing, Chen Changkun. Application and Accuracy Analysis of RBF Neural Network in Regional GPS Height Fitting[J]. Geomatics and Spatial Information Technology, 2018, 41(11): 94-96 DOI:10.3969/j.issn.1672-5867.2018.11.027)
(  0) 0) |
| [11] |
彭中波, 高阳. BP神经网络在水下地形高程拟合的应用[J]. 重庆交通大学学报:自然科学版, 2018, 37(11): 64-68 (Peng Zhongbo, Gao Yang. Application of BP Neural Network in Elevation Fitting of Underwater Terrain[J]. Journal of Chongqing Jiaotong University: Natural Science, 2018, 37(11): 64-68)
(  0) 0) |
| [12] |
束蝉方, 李斐, 李明峰. 基于RBF神经网络的GPS/水准高程异常拟合[J]. 地球物理学进展, 2011, 26(3): 819-823 (Shu Chanfang, Li Fei, Li Mingfeng. GPS/Leveling Quasi-Geoid Fitting Based on RBF Neural Networks[J]. Progress in Geophysics, 2011, 26(3): 819-823 DOI:10.3969/j.issn.1004-2903.2011.03.005)
(  0) 0) |
| [13] |
高宁, 王晓静, 王静燕. 基于RBF神经网络的矿区GPS高程转换研究[J]. 煤炭技术, 2015, 34(10): 110-112 (Gao Ning, Wang Xiaojing, Wang Jingyan. Research on Transformation of GPS Height in Mining Area Based on Radial Basis Function Neural Network[J]. Coal Technology, 2015, 34(10): 110-112)
(  0) 0) |
| [14] |
黄洋, 鲁海燕, 许凯波, 等. 基于S型函数的自适应粒子群优化算法[J]. 计算机科学, 2019, 46(1): 245-250 (Huang Yang, Lu Haiyan, Xu Kaibo, et al. S-shaped Function Based Adaptive Particle Swarm Optimization Algorithm[J]. Computer Science, 2019, 46(1): 245-250)
(  0) 0) |
2. School of Information Engineering, China University of Geosciences, 29 Xueyuan Road, Beijing100083, China
 2020, Vol. 40
2020, Vol. 40


