目前对于区域性的滑坡预测主要以滑坡易发性评价非确定性方法为主[1],但这类方法往往忽视了滑坡灾害的空间性,在没有考虑模型空间适用性的情况下将其推广至整个研究区域,会降低滑坡易发性评价结果的准确性。为解决空间差异性问题,本文利用GWR模型将空间尺度的概念引入到滑坡易发性评价研究中,建立基于GWR-PSO-SVM的滑坡易发性评价耦合模型,揭示空间尺度对滑坡易发性评价结果造成影响的根本原因,解释滑坡易发性评价结果的空间不平衡性,提高滑坡易发性评价的科学性、准确性和可靠性。
1 滑坡易发性评价耦合模型 1.1 地理加权回归模型GWR模型利用回归原理研究具有空间分布特征的2个或多个变量之间的数量关系,将局部特征作为权重从而改变全局回归模型中的多重共线性[2],相关函数定义为:
| $ {{y}_{i}}={{\beta }_{0}}\left( {{\mu }_{i}}, {{v}_{i}} \right)+\sum\limits_{k=1}^{Q}{{{\beta }_{k}}}\left( {{\mu }_{i}}, {{v}_{i}} \right){{x}_{ik}}+{{\varepsilon }_{i}} $ | (1) |
式中,i=1, 2, …, L,(μi, vi)为第i个样本的空间坐标,L和Q分别为样本和回归系数的个数,yi为函数在i点的自变量,xik为i点的第k个解释变量的值,βk(μi, vi)为i点的第k个解释变量的局部回归参数,β0(μi, vi)为i点的截距参数。
1.2 支持向量机模型SVM模型建立在VC维理论和结构风险最小原理基础上,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中,以获得最好的推广能力。该模型在解决小样本、非线性及高维模式识别中具有许多特有的优势[3],其函数定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {\min \frac{1}{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}}\\ {{\mathop{\rm s}\nolimits} .t.\;{y_i}(\mathit{\boldsymbol{w}} \cdot {x_i} + b) \ge 1} \end{array}} \right. $ | (2) |
式中,xi为位于超平面上的点,yi为分类标记,i=1, 2, …, R,R为样本个数,w为一个垂直于超平面的向量,b为使得超平面不会通过坐标轴原点的常数,‖ w‖为w的2-范数。
1.3 粒子群优化算法PSO算法是一种模仿鸟类觅食的智能寻优算法[4],其函数形式为:
| $ \left\{ \begin{align} & V_{i}^{n+1}=t\cdot V_{i}^{n}+{{c}_{1}}\cdot {{r}_{1}}\cdot \left( p_{i}^{n}-x_{i}^{n} \right)+ \\ & \ \ \ \ \ {{c}_{2}}\cdot {{r}_{2}}\left( p_{g}^{n}-x_{i}^{n} \right) \\ & x_{i}^{n+1}=x_{i}^{n}+V_{i}^{n} \\ \end{align} \right. $ | (3) |
式中,i=1, 2, …, k,k为粒子的个数,n为当前迭代次数,t为非负数的惯性权重,pin为第i个粒子的个体最优位置,pgn为第n次迭代中所有粒子的最优位置,Vin和xin分别为第i个粒子在第n次迭代中的速度和位置,Vin+1和xin+1分别为第i个粒子在第n+1次迭代中更新的速度和位置,c1和c2为学习因子,r1和r2为介于0和1之间的随机数。
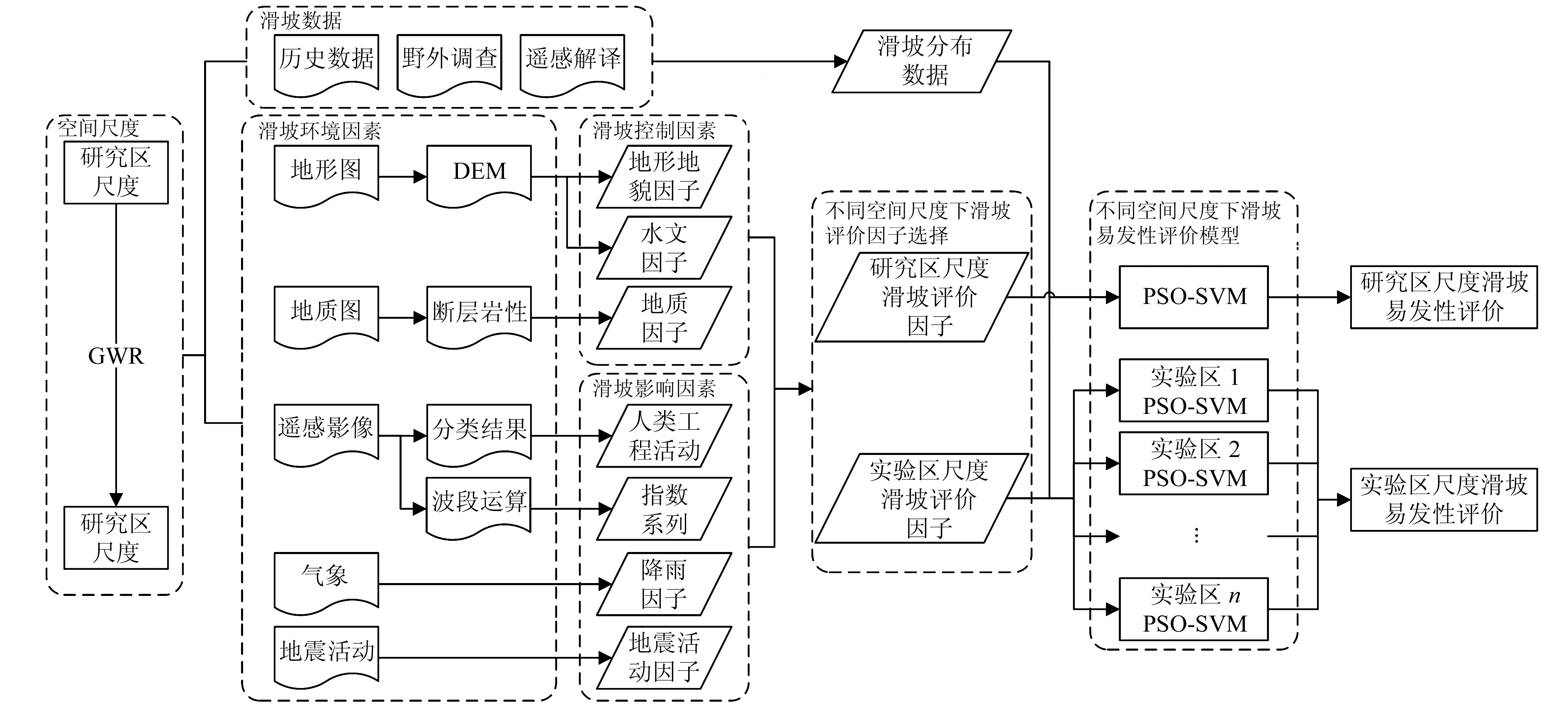
1.4 基于空间多尺度的滑坡易发性评价耦合模型本文以滑坡评价因子的空间自相关性为切入点,将滑坡评价因子的GWR系数作为研究区分割的数学依据,对研究区进行空间尺度分割。以滑坡易发性评价为核心进行模型整合,利用PSO算法对SVM模型进行参数优化。优化后的模型可以考虑到不同空间尺度的评价预测区中滑坡评价因子的实际情况,通过调节滑坡易发性评价模型的参数,可以提高在不同空间尺度下滑坡易发性评价结果的精度,从而实现空间多尺度的滑坡易发性评价模型的建立。图 1为建立基于空间多尺度分析的滑坡易发性评价耦合模型的流程。
|
图 1 建立基于空间多尺度分析的滑坡易发性评价耦合模型流程 Fig. 1 The flow chart of establishing the coupling model for landslide susceptibility evaluation based on spatial multi-scale analysis |
斜坡单元能在一定程度上反映不同的滑坡评价因子对滑坡的控制与影响作用,因此本文选择斜坡单元作为滑坡易发性评价的计算单元,并最终建立了2 790个斜坡单元。
2.2 滑坡易发性评价因子的获取本文通过分析研究区的滑坡历史数据和总结前人的研究成果,将滑坡环境因素(滑坡易发性评价因子)分为控制因素和影响因素2个大类。控制因素包含地形地貌因子、地质因子、水文因子这3个亚类;影响因素包括地表覆被、大气降水及地震活动等几个方面的因子。本文利用地质图、地形图、遥感影像数据、野外勘察报告、典型滑坡监测报告等资料,通过遥感(RS)、地理信息系统(GIS)等技术提取出2个大类8个亚类共计58个滑坡评价因子。
2.3 滑坡易发性评价因子的筛选上述58个因子中有很大一部分是通过数字高程模型(DEM)计算得到的,具有天然的相关性,因此需要对这58个因子进行分析和筛选。主要步骤为:
1) 利用皮尔逊相关系数分析和主成分分析筛选。为了能够保留多因子的有效信息,同时去除这些因子的线性相关性,利用皮尔逊相关系数分析和主成分分析(PCA)方法对因子组合进行处理,保留地形地貌因子的第1、第2和第3主成分,植被指数、湿度指数和建筑指数均保留第1主成分,筛选出32个滑坡易发性评价因子。
2) 基于SVM模型的因子重要性筛选。在SVM模型中,算法会根据滑坡易发性评价因子对滑坡的贡献程度计算出每个因子的重要性。经过反复实验和比对,结合前人研究成果,在包含主要滑坡易发性评价因子的基础上,确定滑坡评价因子的重要性选择阈值(0.005),并最终筛选出18个滑坡易发性评价因子,如表 1所示。
|
|
表 1 筛选后最终的滑坡易发性评价因子 Tab. 1 Final landslide susceptibility evaluation factors after screening |
为保证不同类别之间的地理加权回归系数差异较大,降低类与类之间滑坡评价因子的空间自相关性,在计算得到各滑坡评价因子的GWR系数的基础上,利用自然断点法(natured breaks method)对评价因子进行分类。研究区分割方法理论上应该将所有滑坡评价因子的地理加权回归系数的分类结果进行叠加,得到区域尺度的分割结果,降低每个滑坡评价因子的空间自相关性。但由于滑坡评价因子数目过多,分类结果相叠加会产生许多面积过小的区域,对后续的滑坡易发性评价造成极大的影响。过多的分割区域会使区域与区域之间的空间距离变小,从而在一定程度上增大滑坡评价因子的空间自相关性。经过反复实验,本文总结出在利用GWR模型进行区域分割时需要遵循的3项基本原则:
1) 对所有的滑坡评价因子选择相同且合适的分类数;
2) 仅选择最重要的滑坡评价因子作为分割因子对研究区进行尺度分割;
3) 针对区域分割结果,需要将过小的区域合并到相邻区域中,并且应该保证滑坡面的完整性。
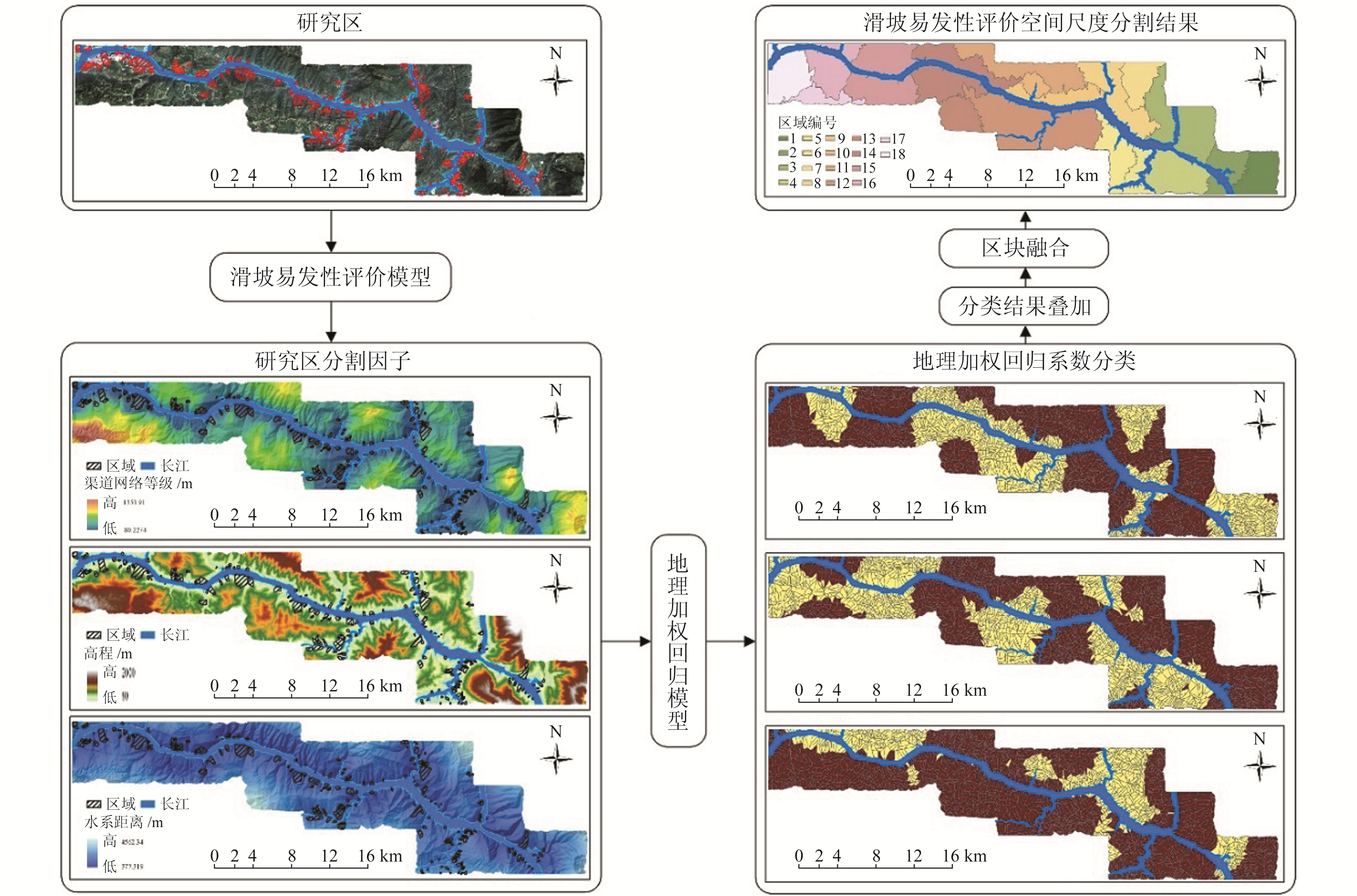
根据上述原则,最终选择SVM模型中重要性排在前3位的滑坡评价因子——渠道网络等级、高程、水系距离作为区域分割因子,并将这3个滑坡评价因子利用自然断点法分成2类相叠加,得到最终的研究区区域尺度分割结果,共计18个预测区域,分割流程如图 2所示。
|
图 2 基于GWR的研究区尺度分割流程 Fig. 2 The process of study area scale segmentation based on GWR |
针对18个预测区域,将每个区域内的滑坡面斜坡单元数量与随机选择的非滑坡面斜坡单元数量按1 :1比例共同组成训练样本数据集,并对PSO-SVM耦合模型进行训练与建模。将区域内的所有斜坡单元作为验证样本数据集,输入到已经训练好的耦合模型中,得到每个斜坡单元对于滑坡事件的隶属度,即预测区域的滑坡易发性评价结果。
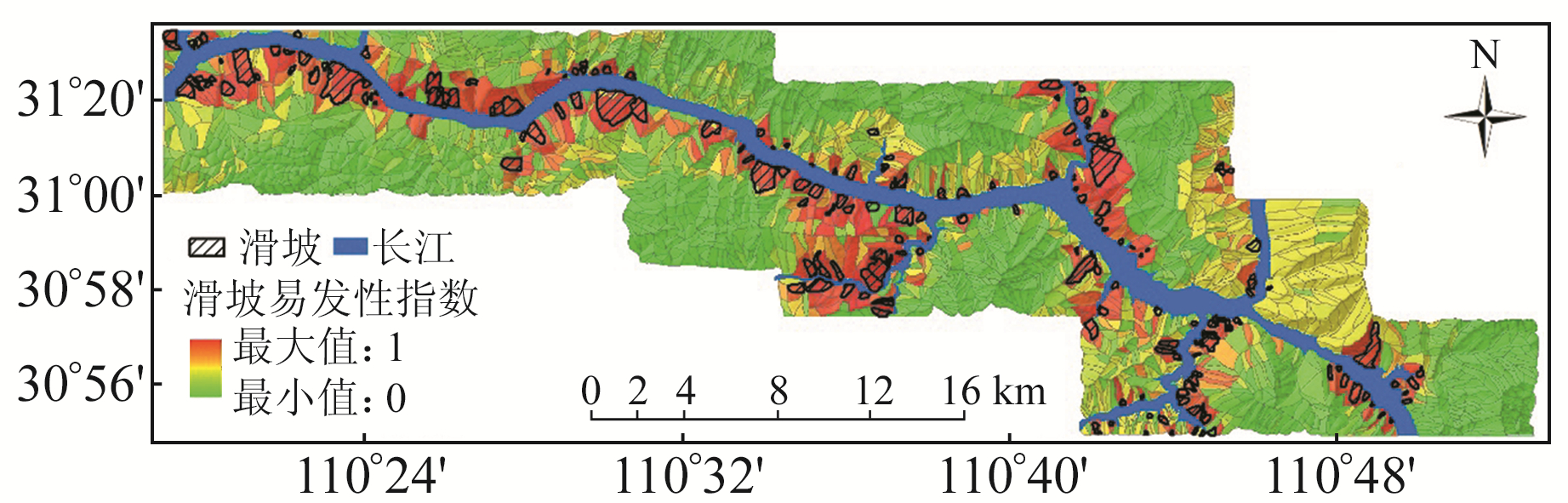
2.6 GWR-PSO-SVM滑坡易发性评价耦合模型实验结果结合所有预测区域的滑坡易发性评价结果,得到基于空间多尺度分析的滑坡易发性评价结果,即GWR-PSO-SVM耦合模型的实验结果(图 3)。
|
图 3 GWR-PSO-SVM耦合模型实验结果 Fig. 3 The experimental results of GWR-PSO-SVM coupling model |
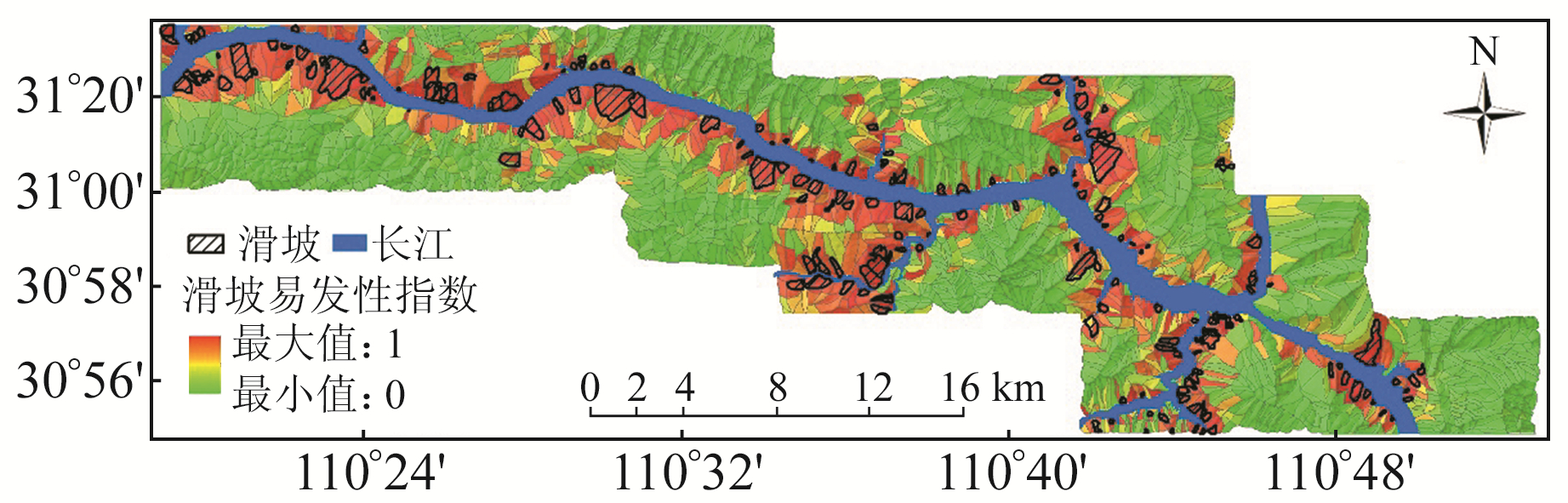
在对比实验中,将PSO-SVM耦合模型作为对比实验组,删除利用GWR系数对研究区进行分割的部分,得到PSO-SVM耦合模型实验结果(图 4)。
|
图 4 PSO-SVM耦合模型实验结果 Fig. 4 The experimental results of PSO-SVM coupling model |
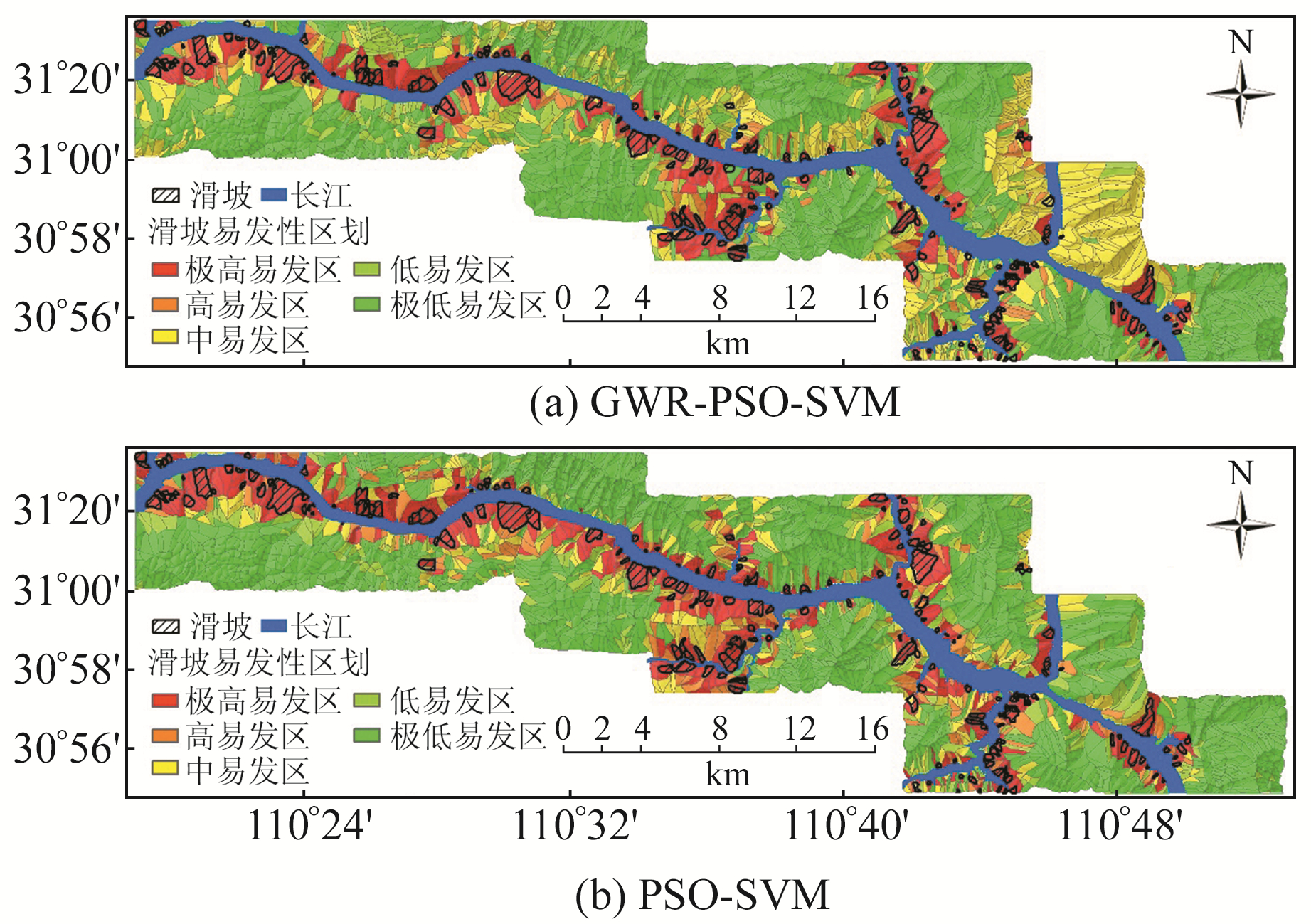
为增强滑坡易发性评价结果的可读性,本文采用固定阈值法,取分类阈值为0.1、0.3、0.7和0.9,得到2组实验的滑坡易发性区划图,如图 5(a)和5(b)所示。
|
图 5 GWR-PSO-SVM和PSO-SVM滑坡易发性区划 Fig. 5 Landslide susceptibility zone map based on GWR-PSO-SVM and PSO-SVM coupling model |
特定类别精度分析法为一种改进的定量分析方法,可以用来解决传统方法不适用的具有两极分化特点的滑坡易发性评价定量分析问题[5],可表示为:
| $ {{p}_{i}}=\frac{{{A}_{i}}}{{{B}_{i}}}\cdot 100% $ | (4) |
式中,i=1, 2, …, n,n为滑坡易发性区划的分类个数,Ai为在第i个滑坡易发性区划分类中滑坡所占斜坡单元的个数,Bi为在第i个滑坡易发性区划分类中斜坡单元的个数,Pi为在第i个滑坡易发性区划分类中的特定类别精度。
根据式(4),2组实验的特定类别精度如表 2所示。
|
|
表 2 2组实验的特定类别精度分析 Tab. 2 Specific category accuracy analysis for two experiments |
从表 2可以看出,在GWR-PSO-SVM耦合模型中,滑坡易发性评价结果(85.75%)要优于PSO-SVM耦合模型的滑坡易发性评价结果(68.35%)。
3.2.2 总体预测精度分析总体预测精度分析是滑坡易发性评价中较为常用的评价方法之一。本文在GWR-PSO-SVM耦合模型分析中采用区域分割的方法对滑坡易发性评价进行研究,而在某些分割区域内不存在滑坡,因此需要对式(4)进行改写:
| $ p=\frac{\sum\limits_{i=1}^{{{n}_{\text{pr}}}}{\left( {{a}_{i}}+{{b}_{i}} \right)}}{\sum\limits_{i=1}^{{{n}_{\text{pr}}}}{{{S}_{i}}}}\cdot 100% $ | (5) |
其中,i=1, 2, …, n,npr为预测区的个数,ai为在第i个预测区内被正确预测为滑坡的斜坡单元个数,bi为在第i个预测区内被正确预测为非滑坡的斜坡单元个数,Si为在第i个预测区内总斜坡单元个数。表 3为2组实验的总体预测精度。
|
|
表 3 2组实验的总体预测精度分析 Tab. 3 Overall prediction accuracy analysis for two experiments |
从表 3可以看出,GWR-PSO-SVM耦合模型的总体预测精度为87.86%,明显优于PSO-SVM耦合模型的84.44%。
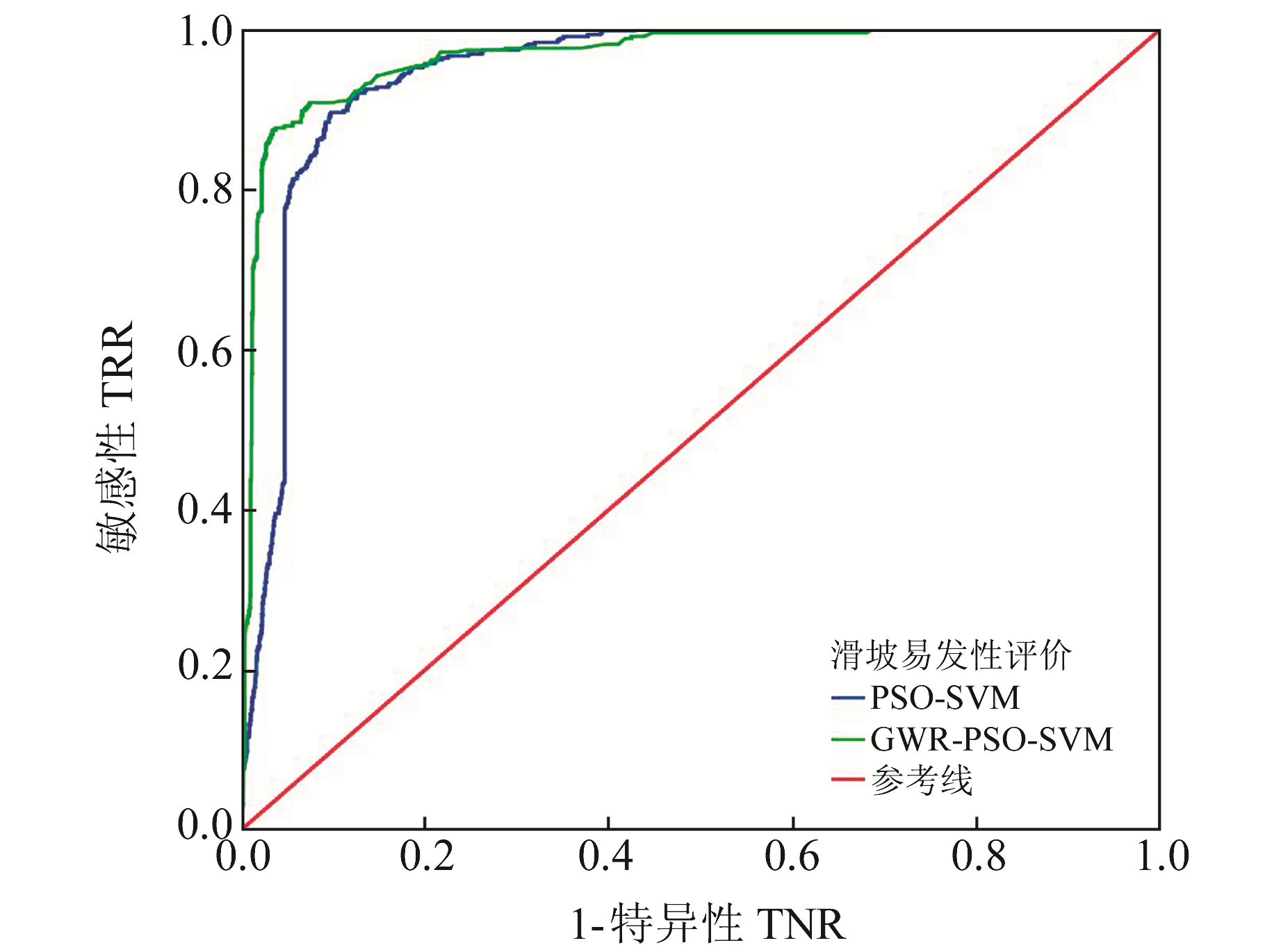
3.2.3 ROC曲线分析ROC曲线分析是统计理论中的经典内容,本文将每个斜坡单元是否为滑坡斜坡单元的真实数据作为状态变量,将连续型的不同尺度下滑坡易发性评价结果作为检验变量,构建ROC曲线(图 6)。
|
图 6 2组实验的ROC曲线 Fig. 6 ROC curve for two experiments |
表 4为这2组实验的滑坡易发性评价结果ROC曲线的曲线下面积(AUC)。
|
|
表 4 2组实验的曲线下面积分析 Tab. 4 AUC analysis for two experiments |
从表 4可以看出,GWR-PSO-SVM耦合模型的曲线下面积为0.965,大于PSO-SVM耦合模型的0.944,说明在ROC曲线评价中,GWR-PSO-SVM耦合模型的结果要优于PSO-SVM耦合模型。
4 实验讨论基于前文的分析及滑坡易发性评价的特点,将对滑坡易发性评价结果造成差异的主要原因归纳为3点,即滑坡易发性评价的空间尺度、滑坡评价因子及预测模型的选择。在同一空间尺度下,导致滑坡易发性评价结果产生差异的主要原因是滑坡评价因子、滑坡易发性评价计算单元及滑坡易发性评价模型。但随着研究的深入和空间尺度问题的引入,滑坡易发性评价的空间尺度、滑坡评价因子及预测模型的选择成为主导滑坡易发性评价结果产生差异的根本原因。
滑坡易发性评价模型本身并不都是地质学或者地理学等相关学科原生的,更多的是借鉴于其他学科领域,如由统计学、数学、经济学等学科演化而来,这些模型经过时间的反复验证,其本身具有客观性、适用性和稳定性。计算单元以栅格单元为基础,栅格单元又是由遥感卫星成像及其数学物理特性决定的,其本身也具有客观性,因此本文的研究目标主要是滑坡易发性评价因子和空间尺度两个方面。
5 实验结论在14组PSO-SVM耦合模型滑坡易发性评价实验中,各滑坡易发性评价因子在其中的重要性各不相同,如图 7所示。为对比方便,图例中的滑坡易发性评价因子是按PSO-SVM耦合模型中滑坡易发性评价因子的重要性评分值倒序排列的(0.241~0.005)。从图 7可以看出:

|
图 7 GWR-PSO-SVM耦合模型中各分割区域滑坡评价因子重要性变化示意图 Fig. 7 Schematic diagram of the significance changes of landslide evaluation factors in each segmented area based on GWR-PSO-SVM coupled model |
1) 在PSO-SVM耦合模型中具有重要性的滑坡易发性评价因子在分割后的某些区域并不存在重要性(其值为0),如斜坡结构、斜坡形态等,甚至在预测区域5中,在区域尺度下排名第1的滑坡评价因子也不存在重要性,这说明在不同空间尺度下滑坡易发性评价因子的重要性存在差异。
2) 研究区分割后,相邻编号之间存在较为相近甚至相邻的空间位置关系。但在图 7中,即使是相邻的区域2和区域3,其滑坡评价因子的重要性排序也都大不相同,表明滑坡评价因子的重要性在不同预测区域的变化及滑坡评价因子的局部性特点。
6 结语综上所述,不同区域的滑坡易发性评价因子其实是不同的。将整个研究区的滑坡易发性评价因子先通过模型进行统计计算再赋权重值的方法显然是存在问题的,其本质还是在于研究区的空间尺度影响着滑坡易发性评价因子的重要性。因此,以滑坡易发性评价因子为基础,利用GWR理论计算得到主要因子的GWR系数,再通过GWR系数分类、重要因子叠加、人机交互修改等步骤得到的研究区空间尺度分割方法,是解决这一问题行之有效的方法。
| [1] |
Mondal S, Mandal S. RS&GIS-Based Landslide Susceptibility Mapping of the Balason River Basin, Darjeeling Himalaya, Using Logistic Regression (LR) Model[J]. Georisk:Assessment and Management of Risk for Engineered Systems and Geohazards, 2018, 12(1): 29-44 DOI:10.1080/17499518.2017.1347949
(  0) 0) |
| [2] |
Fotheringham A S, Charlton M E, Brunsdon C. Geographically Weighted Regression:A Natural Evolution of the Expansion Method for Spatial Data Analysis[J]. Environment and Planning A, 1998, 30(11): 1905-1927 DOI:10.1068/a301905
(  0) 0) |
| [3] |
Vapnik V. The Nature of Statistical Learning Theory[M]. New York: Springer-Verlag, 2000
(  0) 0) |
| [4] |
Eberhart R, Kennedy J. A New Optimizer Using Particle Swarm Theory[C]. The Sixth International Symposium on Micro Machine and Human Science, Nagoya, 1995
(  0) 0) |
| [5] |
于宪煜.基于多源数据和多尺度分析的滑坡易发性评价方法研究[D].武汉: 中国地质大学(武汉), 2016 (Yu Xianyu. Study on the Landslide Susceptibility Evaluation Method Based on Multi-Source Data and Multi-Scale Analysis[D]. Wuhan: China University of Geosciences, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10491-1016312027.htm
(  0) 0) |
 2019, Vol. 40
2019, Vol. 40

