我国地震的重力监测以地表重力测量为主,虽然现有的重力监测体系在地震预测中取得了一定成果,但仍存在一些问题:1)时间分辨率低,每年2~3期的观测对于强震有一定的监测能力,但对于5级以下地震的监测能力不足[1];2)作业效率低,受地面环境影响较大;3)以人工测量为主,未来智能化发展潜力较低。因此,发展新的重力监测手段有助于我国地震监测事业的发展。
邻近空间(near space)是指距离地面20~100 km的空域[2],横跨平流层、中间层和部分电离层,这个空域的飞行器具有可持续观测、使用周期长等优点。我国自主研发的彩虹系列邻近空间飞行器为地球科学相关观测提供新的载荷平台,该系列无人机具有航时长、布设灵活、经济优势明显等特点。以邻近空间无人飞行器为平台建立的重力观测系统,相较于地面测量更加高效,邻近空间更为稳定的环境使其相对于传统航空重力测量更加精准,与卫星重力测量相比则更加灵活、分辨率更高[3-4],是立体地震重力监测系统的重要一环。
本文从地震监测的实际需求出发,探讨邻近空间重力测量系统在未来地震监测中的可能应用。以震前变化为例,使用位场延拓计算地面重力在邻近空间的变化量,探讨邻近空间重力测量系统在地震监测应用方面的精度需求,为未来邻近空间重力测量平台系统的开发提供参考。
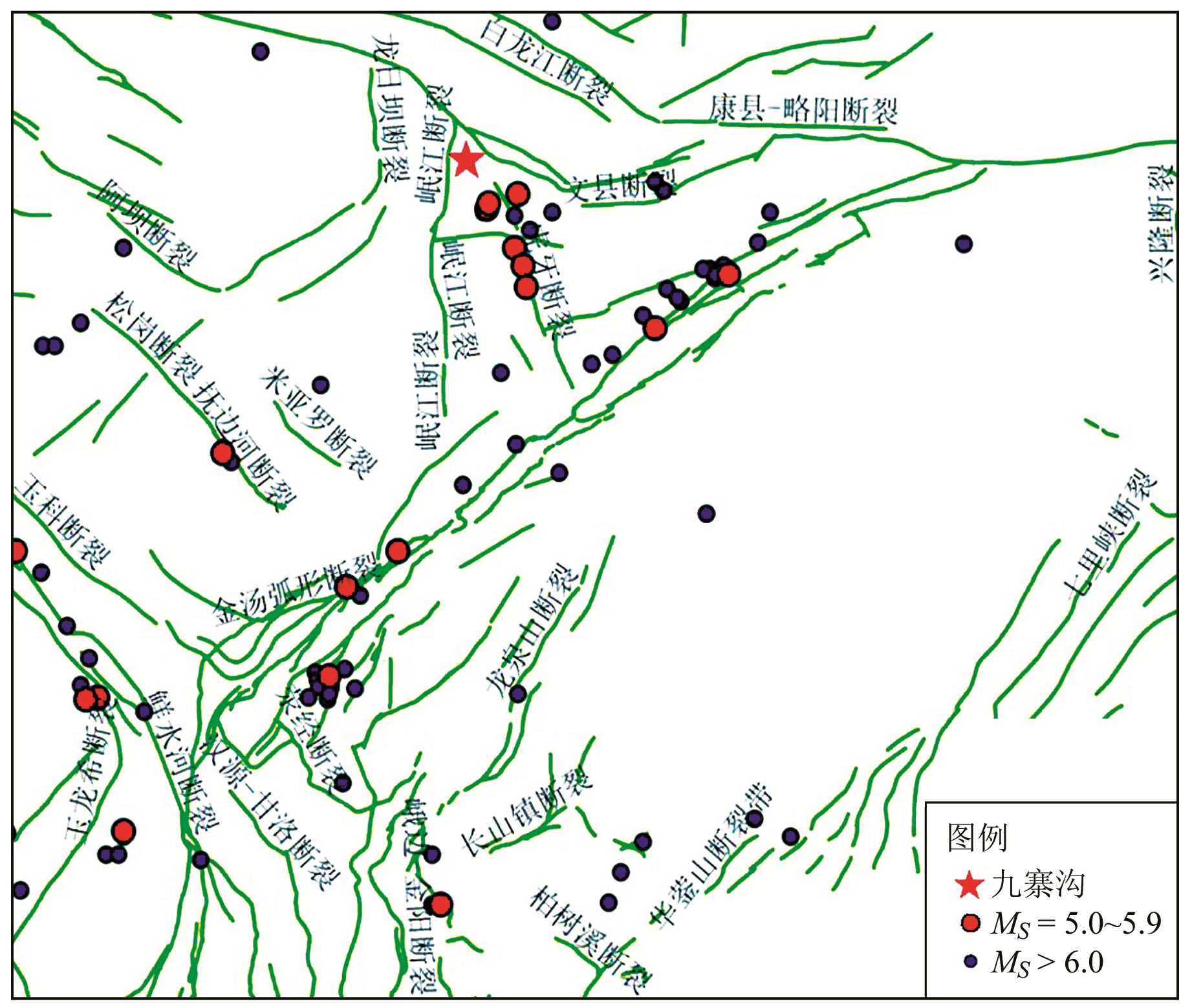
1 数据来源及九寨沟地震概况九寨沟M7.0地震位于103.8°E、33.2°N,震源深度约为20 km。从地质构造上看(图 1),九寨沟地震震中位于东昆仑断裂带东端,震中区域附近存在多条已知活动断裂带,包括岷江断裂、塔藏断裂及虎牙断裂等[5]。谢祖军等[6]认为九寨沟地震是一个以走滑为主的地震,地震破裂没有到达地表,发震断层位于东昆仑断裂带的转换区域。
|
图 1 九寨沟地震震中附近区域构造特征及历史强震 Fig. 1 Violent earthquakes in history and tentonic characteristics around the epicenter of the Jiuzhaigou earthquake |
中国地震局对南北地震带的观测十分重视,通过优化和整合各级地震重力监测网络,于2013年建立了覆盖整个南北地震带的流动重力监测网。九寨沟周边地区从2014年第1期观测开始,以每年2期的观测频率进行流动重力观测,至九寨沟地震发生前,一共有7期观测资料。九寨沟地震的震中位置在该监测网的中部,震中500 km范围内共有约500个流动重力观测点及10个连续重力观测台。
在2017-06的全国地震趋势会商会上,重力观测技术部的专家根据观测到的重力场变化对九寨沟7.0级地震进行了较好的年度预测[7],本文根据相关资料绘制了九寨沟地震震前重力变化图(图 2、3),图中黑点为流动重力观测点。

|
图 2 四川地区测点分布及九寨沟地震震前1~3 a尺度重力场变化 Fig. 2 Survey station in Sichuan and the gravity changes of 1 to 3 years in Jiuzhaigou district |
|
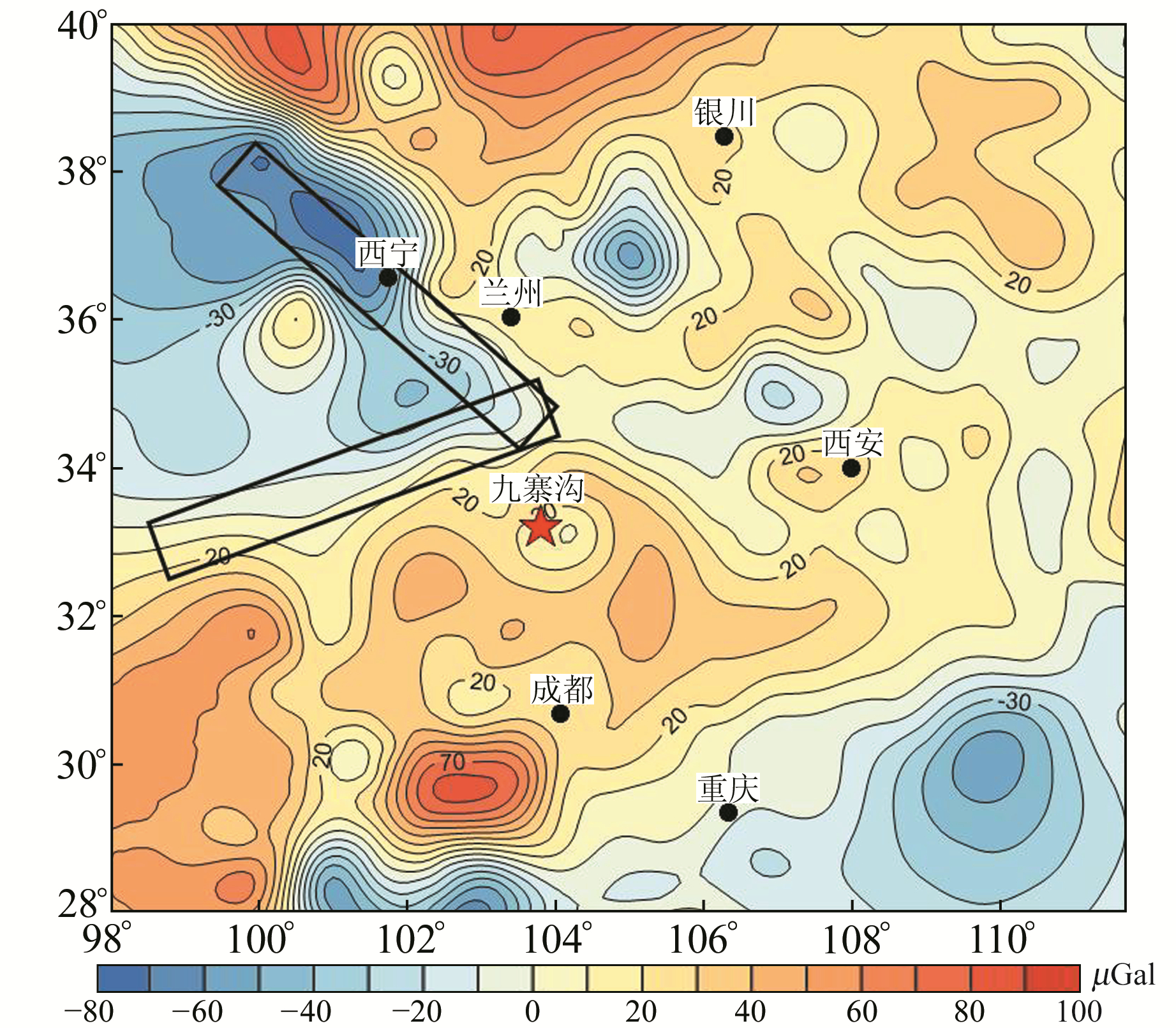
图 3 九寨沟地震震前2016-10~2017-04重力变化 Fig. 3 The gravity changes before Jiuzhaigou earthquake of 2016-10 to 2017-04 |
图 2(a)为1 a尺度流动重力变化(2014-04~2015-04),图 2(b)为2 a尺度流动重力变化(2014-04~2016-04),图 2(c)为3 a尺度流动重力变化(2014-04~2017-04)。从图 2(a)中可以看出,重力场变化自西向东呈现明显的由负到正的变化趋势,且正负变化的分界线明显分布于柴达木块体、祁连块体等活动块体的边界处;在图 2(b)中,重力变化展现出与1 a尺度相似的变化趋势,但负变化数值明显增大,由70 μGal增大到100 μGal;图 2(c)中的重力场仍保持相同的变化趋势,但是变化梯度零值线弯折现象更为明显。通过1~3 a尺度的图像分析可以看出,重力变化有较好的继承性,随着时间的积累,各时段重力变化基本维持自西向东、由负到正的趋势变化,且特征逐渐明显。图 3为九寨沟地震发震前最新一期的重力变化图像,可以看出,龙门山断裂带两侧重力变化由之前的负变化转为正变化,打破了3 a来的累积趋势,可认为是该区域地震发生危险性增强的信号。
2 向上延拓方法目前用于重力场延拓的主要方法一般有两类:1)波数域延拓计算方法;2)空间域延拓计算方法[8]。波数域延拓计算方法首先通过傅里叶变换求得重力场频谱,再将其与对应频域的响应函数相乘,最后通过傅里叶逆变换求得延拓结果,具体算法有傅里叶变换法、余弦变换法等[9]。空间域延拓计算方法是以诺伊曼无限平面外部问题为理论基础,将离散化的无限平面分成若干矩形方块,通过积分求解延拓结果,具体算法有积分插值法、数值积分法、样条函数法[10]、积分迭代法等。波数域方法收敛速度快、易于实现,但其精度较低;空间域方法原理简单、精度较高,但计算复杂、求解效率低,在求解局部重力场向上延拓的过程中,边界效应显著。
周清强[11]认为空间域延拓计算方法无需对离散化数据进行频谱变换,原理相对简单,精度更高,受地形影响相对较小;若采用以线性反演理论为基础的空间域延拓计算方法,则需求解大量线性方程组,在实际计算中过于复杂且耗时较长。本文通过泊松积分原理将样本区域离散化并适度外扩,进而进行地表重力变化向上延拓至邻近空间的计算。
已知球面上任意一点的重力异常值,求解空间中待定点的重力异常值,这一过程可看作求解Dirichlet问题(泊松积分即为Dirichlet问题的解[12])。如果地表σ上任意一点P的重力异常值为ΔgP,则空间中任意一点Q的重力异常值ΔgQ可以用式(1)表示:
| $ \begin{matrix} \Delta {{g}_{Q}}(r, \theta , \lambda )= \\ \frac{R\left( {{r}^{2}}-{{R}^{2}} \right)}{4\pi }\iint_{\sigma }{\frac{\Delta {{g}_{P}}\left( R, {{\theta }^{\prime }}, {{\lambda }^{\prime }} \right)}{{{l}^{3}}}}\text{d}\sigma \\ \end{matrix} $ | (1) |
式中,r、θ、λ为空间点Q在球坐标系下的坐标,R、θ′、λ′为地表点P在球坐标系下的坐标,l为两点之间的几何距离,其中,
| $ l=\sqrt{{{r}^{2}}+{{R}^{2}}-2Rr\cos \varphi } $ | (2) |
式中,φ为P、Q两点之间的角距。
本文将球面问题简化成无限平面求解。对式(1)进行离散化处理得:
| $ \Delta {{g}_{Q}}\left( {{x}_{0}}, {{y}_{0}}, {{z}_{0}} \right)=\frac{hs}{2\pi }\sum\limits_{i=1}^{n}{\frac{\Delta {{g}_{p}}\left( {{x}_{i}}, {{y}_{i}} \right)}{l_{i}^{3}}} $ | (3) |
式中,s为矩形网格面积。王丹等[13]给出延拓高度对矩形网格面积的约束关系,其表达式为:
| $ \frac{s}{{{h}^{2}}}<2\pi $ |
本文主要研究邻近空间重力变化的特征及其在地震研究中的发展潜力,数据来源于2017年九寨沟地震震前周边包括四川、重庆、陕西、甘肃、青海等区域的重力变化(表 1),利用式(3)计算重力变化延拓,延拓高度选择为20 km、30 km、40 km、50 km、60 km,并与地面重力变化进行比较,最后分析结果。
|
|
表 1 重力变化网格参数 Tab. 1 Grid parameters of the gravity changes |
图 4、5、6分别为1 a、2 a、3 a尺度下的重力变化,分图(a)、(b)、(c)、(d)、(e)分别对应20 km、30 km、40 km、50 km、60 km的高度;图 7为3 a尺度的地表重力变化分别在80 km(a)、90 km(b)、100 km(c)高度的延拓结果(以2014-04第1期数据为基准)。与图 2对比可以看出,1~3 a尺度重力变化的地面变化复杂特征相对不突出;当重力变化向上延拓到20 km时,浅源变化如地形效应被过滤掉,内部结构变化导致的质量重新分布引起的重力变化更加明显,九寨沟地震震中明显位于重力变化零值带上;而在20~60 km过程中,虽然重力变化进一步衰减,但主要特征保持不变,重力变化呈现自西向东、由负到正的变化趋势。对于地震危险性研究而言,地球内部的质量迁移引起的重力变化更值得关注,因此在邻近空间观测到的重力变化图像适用于地震危险性研究。计算结果表明,当地面有约70 μGal的重力变化时,在20 km处约产生18 μGal的变化值,因此当邻近空间飞行器在20 km高度进行测量时,最好能分辨出10 μGal的重力变化。

|
图 4 2014~2015年地表重力变化延拓到邻近空间 Fig. 4 Gravity changes on the ground of 2014 to 2015 upward continuation to near space |

|
图 5 2014~2016年地表重力变化延拓到邻近空间 Fig. 5 Gravity changes on the ground of 2014 to 2016 upward continuation to near space |

|
图 6 2014~2017年地表重力变化延拓到邻近空间 Fig. 6 Gravity changes on the ground of 2014 to 2017 upward continuation to near space |

|
图 7 2014~2017年地表重力变化在80~100 km高度的延拓 Fig. 7 Gravity changes in the near space (80 to 100 km) of 2014 to 2017 |
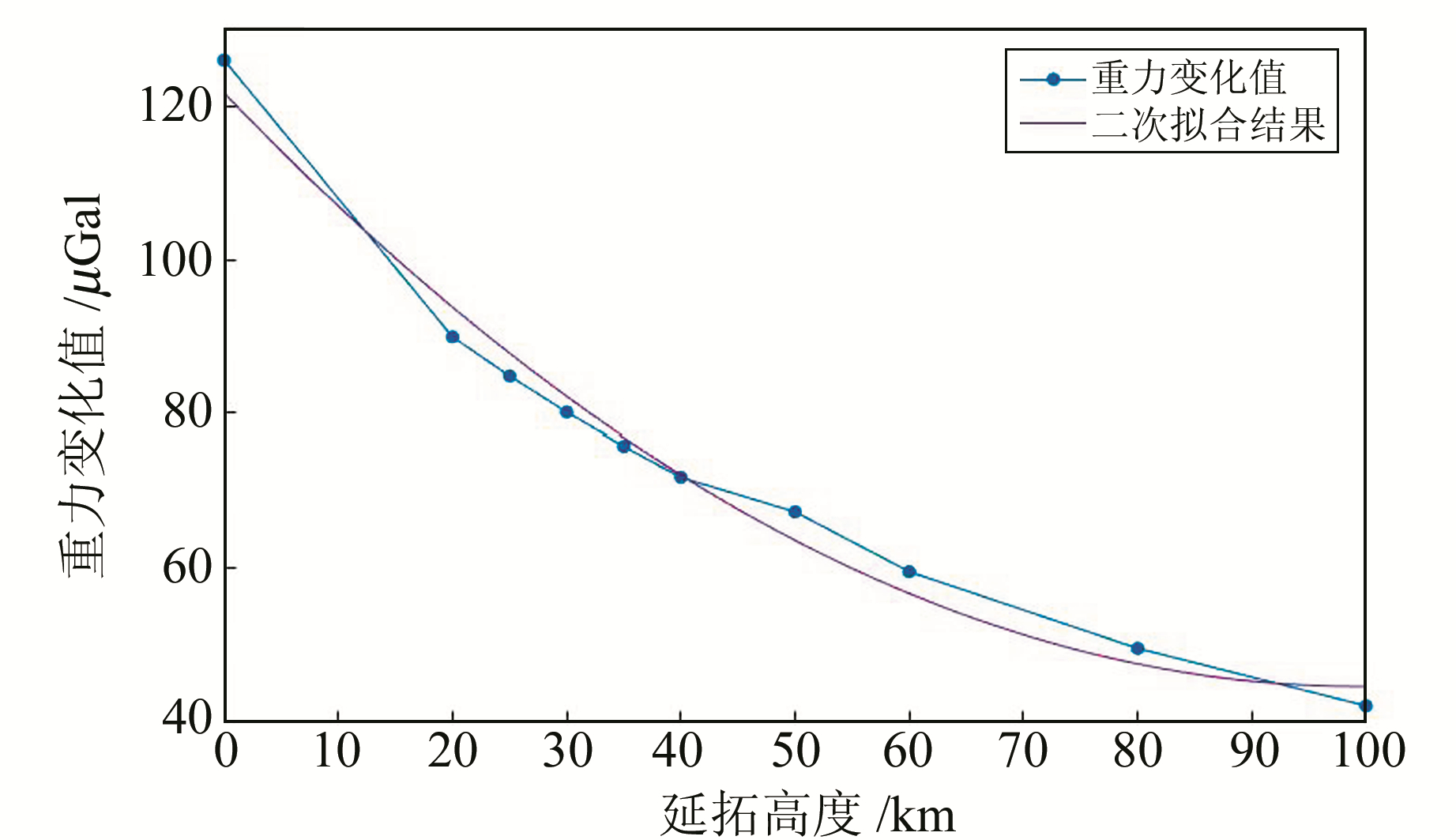
为体现出重力变化在不同延拓高度的变化特征,选取一点(104°E,40.1°N,3 a尺度)绘制重力随延拓高度的变化图并进行拟合(图 8)。从图 8可以看出,重力变化衰减率在0~20 km时最大,并随着高度的增加逐渐减缓,体现重力场与距离呈平方比衰减的特性。当地表变化值为126 μGal时,延拓到20 km高度衰减为90 μGal;当延拓高度为100 km时,依然有42 μGal的重力变化。
|
图 8 不同高度重力变化延拓值 Fig. 8 Upward continuation value of gravity change at different height |
综上所述,邻近空间飞行器在20 km高度进行地震监测时,传感器分辨率最好优于100 μGal。
4 结语流动重力测量是目前地震监测中重力数据的主要来源,但其存在着作业效率不高等问题,每年2~3期的重力观测对于地震研究来说远远不够。以智能化无人机为平台的邻近空间重力测量能弥补这一缺点,并提高重力数据的时间覆盖率。
本文以九寨沟地震震前的重力变化为例,利用以离散泊松积分为原理的向上解析延拓方法计算邻近空间的重力变化。从结果可以看出,邻近空间重力测量具有监测地震的潜力,但作为一个全新的技术手段,邻近空间重力测量技术还面临许多问题。为深入讨论该技术在地震监测中的应用,未来将进一步研究大气模型改正、轨道稳定性改正、飞行姿态改正、固体潮改正等问题。
| [1] |
胡敏章, 李辉, 刘子维, 等. 川滇地区2010~2013年重力变化及重力网的地震监测能力[J]. 大地测量与地球动力学, 2015, 35(4): 616-620 (Hu Minzhang, Li Hui, Liu Ziwei, et al. The Gravity Change over Sichuan-Yunnan Region in 2010-2013 and the Earthquake Monitoring Ability of the Gravimetric Network[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 616-620)
(  0) 0) |
| [2] |
沈海军, 陈凯, 杨莉. 近空间飞行器[M]. 北京: 航空工业出版社, 2012 (Shen Haijun, Chen Kai, Yang Li. Near Space Aerocraft[M]. Beijing: Aviation Industry Press, 2012)
(  0) 0) |
| [3] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field:Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B12): 30205-30229 DOI:10.1029/98JB02844
(  0) 0) |
| [4] |
Chen J L, Wilson C R, Tapley B D. Satellite Gravity Measurements Confirm Accelerated Melting of Greenland Ice Sheet[J]. Science, 2006, 313(5795): 1958-1960 DOI:10.1126/science.1129007
(  0) 0) |
| [5] |
Xu X W, Wen X Z, Yu G H, et al. Coseismic Reverse-and Oblique-Slip Surface Faulting Generated by the 2008 MW 7.9 Wenchuan Earthquake, China[[J]. Geology, 2009, 37(6): 515-518 DOI:10.1130/G25462A.1
(  0) 0) |
| [6] |
谢祖军, 郑勇, 姚华建, 等. 2017年九寨沟MS7.0地震震源性质及发震构造初步分析[J]. 中国科学:地球科学, 2018, 48(1): 79-92 (Xie Zujun, Zheng Yong, Yao Huajian, et al. Preliminary Analysis on the Source Properties and Seismogenic Structure of the 2017 MS7.0 Jiuzhaigou Earthquake[J]. Scientia Sinica Terrae, 2018, 48(1): 79-92)
(  0) 0) |
| [7] |
祝意青, 梁伟锋, 赵云峰, 等. 2017年四川九寨沟MS7.0地震前区域重力场变化[J]. 地球物理学报, 2017, 60(14): 4124-4131 (Zhu Yiqing, Liang Weifeng, Zhao Yunfeng, et al. Gravity Changes before the Jiuzhaigou, Sichuan, MS7.0 Earthquake of 2017[J]. Chinese Journal of Geophysics, 2017, 60(10): 4124-4131 DOI:10.6038/cjg20171037)
(  0) 0) |
| [8] |
张凤旭, 姜正奎, 张凤琴, 等. 利用余弦变换计算重力异常的向上延拓[J]. 地球物理学进展, 2007, 22(1): 57-62 (Zhang Fengxu, Jiang Zhengkui, Zhang Fengqin, et al. Calculating Upward Continuation of Gravity Anomalies Using Cosine Transform[J]. Progress in Geophysics, 2007, 22(1): 57-62 DOI:10.3969/j.issn.1004-2903.2007.01.007)
(  0) 0) |
| [9] |
汪炳柱. 用样条函数法求重力异常二阶垂向导数和向上延拓计算[J]. 石油地球物理勘探, 1996, 31(3): 415-422 (Wang Bingzhu. Computing the Vertical Second Derivative and Upward Continuation of Gravity Anomaly by Spline Function Method[J]. Oil Geophysical Prospecting, 1996, 31(3): 415-422)
(  0) 0) |
| [10] |
邱耀东, 聂琳娟, 张兵兵. 局部重力异常向上延拓的实用算法[J]. 测绘科学, 2017, 42(4): 39-42 (Qiu Yaodong, Nie Linjuan, Zhang Bingbing. A Practical Algorithm for Upward Continuation of Local Gravity Anomalies[J]. Science of Surveying and Mapping, 2017, 42(4): 39-42)
(  0) 0) |
| [11] |
周清强.位场空间换算的研究与应用[D].成都: 成都理工大学, 2009 (Zhou Qingqiang. The Research and Application of the Potential-Field Space Conversion[D]. Chengdu: Chengdu University of Technology, 2009) http://d.wanfangdata.com.cn/Thesis/D066774
(  0) 0) |
| [12] |
Hofmann-Wellenhof B, Moritz H. Physical Geodesy[M]. New York: Springer, 2006
(  0) 0) |
| [13] |
王丹, 李辉, 申重阳, 等. 地面重力时空变化向卫星高度的解析延拓[J]. 大地测量与地球动力学, 2005, 25(2): 69-74 (Wang Dan, Li Hui, Shen Chongyang, et al. Upward Continuation of Ground Gravity Space-Time Change to Satellite Height[J]. Journal of Geodesy and Geodynamics, 2005, 25(2): 69-74)
(  0) 0) |
 2019, Vol. 40
2019, Vol. 40

