2. 中国地震局地壳应力研究所武汉科技创新基地, 武汉市洪山侧路40号, 430071
利用潮汐参数进行地震预测预报工作由来已久,学者们多致力于研究潮汐对地震的触发作用,利用形变观测探讨固体潮与地震关系的研究较多[1-7],而利用重力固体潮进行探讨的研究则甚少。
震前潮汐时间和空间变化特征与地震到底具有何种关系,一直是困扰重力工作者的重要问题。本文精细处理计算芦山7.0级地震前潮汐时间变化信号,分析提取孕震相关信号,为利用连续重力测量进行地震预测和机理研究提供震例参考。
1 连续重力观测数据本文收集芦山地震前(2011-06~2013-03)距离震中800 km范围内19个连续重力台站(图 1)的连续重力数据,具体情况见表 1。

|
图 1 台站分布 Fig. 1 The distribution of seismic stations |
|
|
表 1 震区连续重力观测站仪器与运行简况 Tab. 1 Instruments and operation profile of continuous gravity observation stations in earthquake zone |
采用Tsoft软件处理台站重力原始数据中的各种干扰(如尖峰、地震、台阶、突跳和间断等),由表 1可知,除了成都台、昭通台和南山台,其余台站的数据都是秒采样。根据不同的干扰信号运用不同的修正器进行修正,先对明显的干扰信号进行修正(如地震、尖峰等),再按10 s间隔降采样得到固体潮观测数据。重复上述去干扰的步骤,得到较平滑的信号。接着按60 s间隔降采样得到分钟采样的固体潮观测数据,继续重复上述去尖峰、阶跃和间断等干扰信号的步骤,得到消去明显干扰信号的观测值。成都台、昭通台和南山台的分钟采样数据则直接进行去干扰处理。最后,将去除明显干扰信号的分钟采样观测信号降采样成小时值。
2.2 数据质量评价应用Nakai拟合模型对预处理后的重力固体潮观测数据进行拟合检验。Nakai拟合是在固体潮理论的基础上,以重力的潮汐理论值作为标准对观测数据进行异常检验。设重力固体潮观测值为y(t), 其Nakai拟合模型[8]为:
| $y(t) = aR(t) - b\frac{{{\rm{d}}R(t)}}{{{\rm{d}}t}} + {k_0} + {k_1}t + {k_2}{t^2}$ | (1) |
式中, R(t)为固体潮理论值,a为潮汐因子,b为未知参数,k0、k1、k2分别为拟合多项式各阶的系数。实际操作中,取时长N=48 h,用最小二乘法解算,即可对重力固体潮资料进行Nakai拟合检验和分析。
经Nakai检验,玉树台的数据记录缺失近10个月,昭通台的数据记录缺失近12个月,计算得到的观测值残差大于2倍均方差值的概率达到55.2%,未达到固体潮观测资料所需的质量,无法满足后续固体潮调和分析的需要,故本文不考虑这2个台站。其余台站的观测值残差小于2倍均方差值的概率均超过85%,说明预处理数据可靠。
2.3 重力潮汐数据调和分析方法国内外广泛应用的潮汐数据调和分析方法主要有Venedikov(VAV)、Eterna和Baytap-G&L等。
VAV调和分析采用长度为48阶带通奇偶滤波器,分别滤出日波、半日波和1/3日波的潮汐分量,然后进行最小二乘法估计,确定潮汐因子δ和相位滞后Δφ。主要波群的分离公式为:
| ${M_i} = \sum\limits_{j = 1}^{363} {{{\bar C}_j}{h_j}\left[ {{\xi _j}\cos {\varphi _j}\left( {{T_i}} \right) + {\eta _j}\sin {\varphi _j}\left( {{T_i}} \right)} \right]} $ | (2) |
| ${N_i} = \sum\limits_{j = 1}^{363} {{{\bar S}_j}{h_j}\left[ { - {\xi _j}\sin {\varphi _j}\left( {{T_i}} \right) + {\eta _j}\cos {\varphi _j}\left( {{T_i}} \right)} \right]} $ | (3) |
| $\xi {\rm{ = }}\delta \cos \Delta \varphi $ | (4) |
| $\eta {\rm{ = }}\delta \sin \Delta \varphi $ | (5) |
式中,363为可分离的潮波分量群数,Cj和Sj为滤波器C和S对不同波的选择因子或振幅因子,Ti为第i个48 h段的中央时刻。VAV调和分析方法可以分析有间断的数据,更符合现有的数据特征。
Eterna调和分析方法中的最小二乘估算分析得到的各参数并不是最优估计;Baytap-G & L调和分析方法与其他方法相比,其确定的漂移项是光滑的,与实际测量的数据不符,会导致调和分析计算得到的结果不准确。由于VAV调和分析允许数据有间断,可以处理完全非均匀采样的观测数据,提高了软件处理实际观测数据的能力,且操作简单,计算结果精度更高[9],故本文采用VAV调和分析方法进行计算。
3 重力潮汐参数分析 3.1 潮波背景分析较长时间的观测数据的潮波分析往往代表测站潮波的背景,可作为潮波时间变化的参考。利用VAV调和分析方法对17个台站预处理后的重力潮汐数据(2011-06~2013-03)作一次性潮汐参数求解,每个台站经过调和分析计算都得到12个主要波群的潮汐参数,其中含有6个日波群、5个半日波群及1个1/3日波群,以格尔木台为例给出其调和分析结果(表 2)。
|
|
表 2 格尔木台VAV调和分析结果 Tab. 2 VAV harmonic analysis results of Golmud |
根据计算结果可知,半日波群中的M2波精度最高,相对更稳定;日波群中O1波次之,其他台站的调和分析结果亦类似。
图 2为17个台站O1波和M2波潮汐因子每月值计算得出的方差的统计情况,可以看出, M2波潮汐因子的方差比O1波潮汐因子精度更高。2011-06~2013-03除了贵阳台、姑咱台和西安台以外,M2波潮汐因子的变化均稳定在0.02‰之内,而O1波潮汐因子的变化绝大多数都稳定在0.6‰之内,所以,半日波M2波潮汐因子比日波O1波潮汐因子更稳定。

|
图 2 O1、M2波潮汐因子方差统计 Fig. 2 Variance statistical of tidal factors of O1 and M2 waves |
重力潮汐参数反映了地球对月亮、太阳及其他近地天体引潮力的响应,主要取决于地球内部物质的空间分布和粘弹性特征[10]。高精度重力潮汐参数的确定不仅可以为重力仪器的标定提供潮汐基准,也可以为重力测量提供潮汐改正参数,同时精密重力潮汐参数的空间分布也可为地球内部精细结构特征提供重要约束,对研究地球内部构造环境具有重要的科学意义。
利用VAV调和分析方法以月为单位对17个台站的重力观测数据(2011-06~2013-03)进行计算,得到一系列潮波的潮汐因子。图 3和4为17个连续重力台站在芦山MS7.0地震前(2011-06~2013-03)M2波潮汐因子随时间变化的曲线。
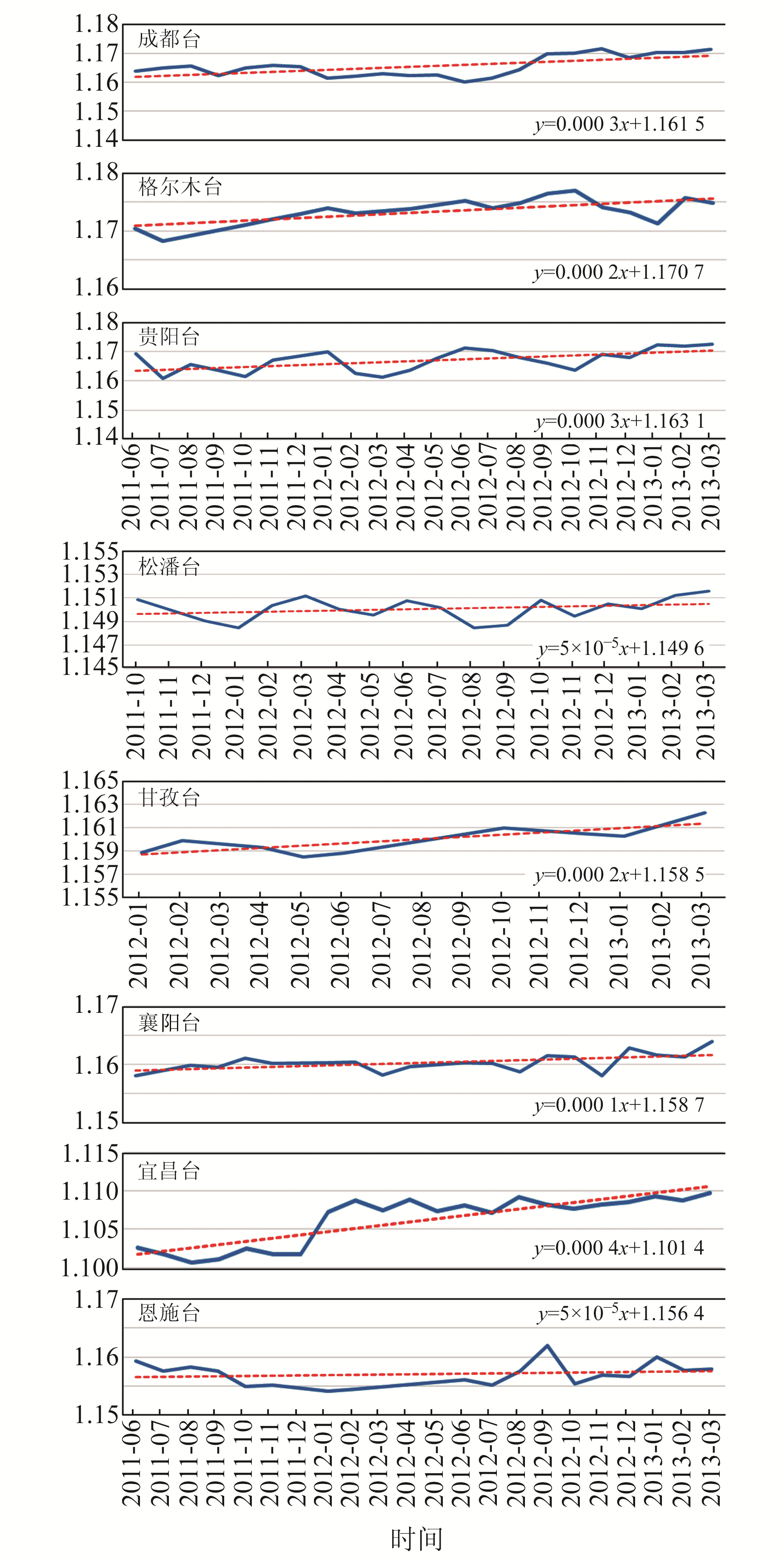
|
图 3 8个台站M2波潮汐因子变化趋势 Fig. 3 Trends of M2 wave tidal factors in 8 stations |
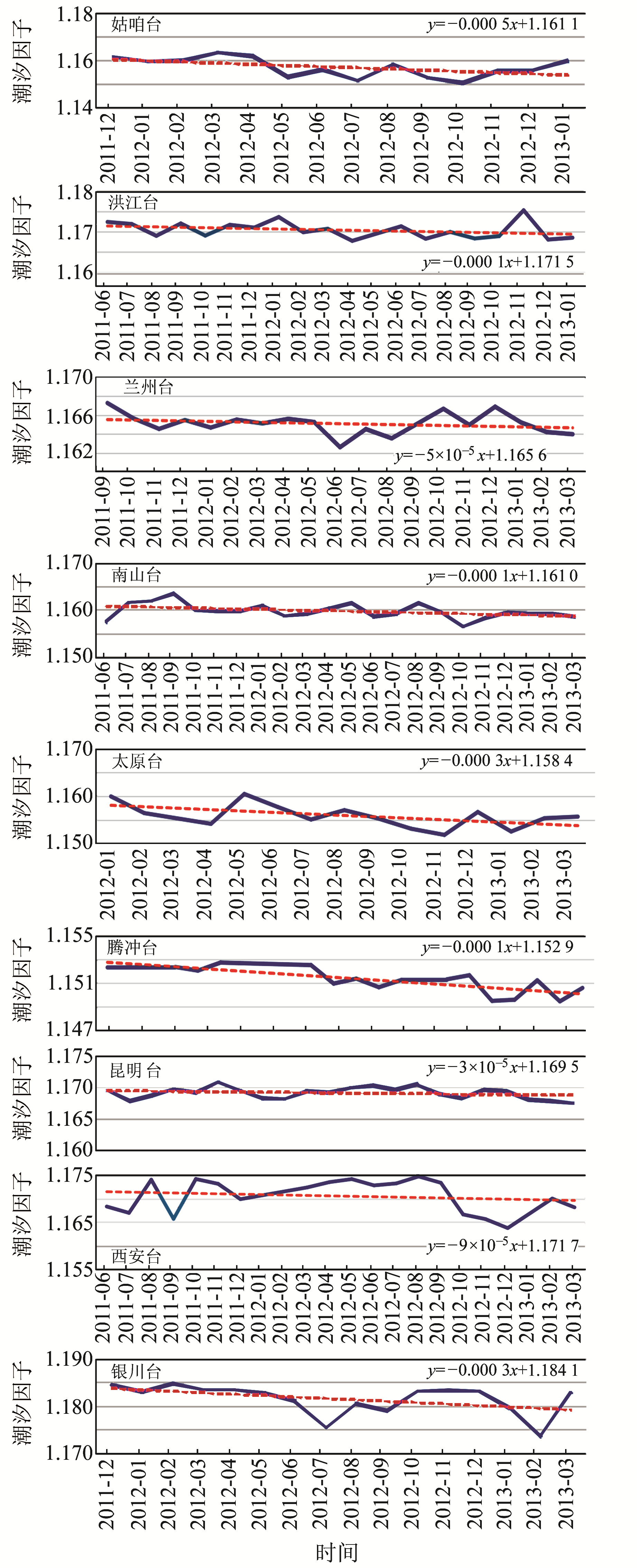
|
图 4 9个台站M2波潮汐因子变化趋势 Fig. 4 Trends of M2 wave tidal factors in 9 stations |
从图 3可以看出,成都台、格尔木台、贵阳台、松潘台、甘孜台、襄阳台、宜昌台、恩施台等8个台站的M2波潮汐因子整体随时间呈现上升的趋势。潮汐因子的变化反映了地壳弹性特征的变化,潮汐因子变化增大表明实际观测的潮波振幅比平均潮波振幅要大,表明该区域的弹性特征增强;反之,则表明该区域的弹性特征较弱。根据历史震例总结认为,当潮汐因子变化达到3%时,周边30 km范围内存在发生6级以上地震的可能[11],图 3中M2波潮汐因子的变化大约在1%以内。
从图 4可以看出,姑咱台、洪江台、兰州台、南山台、太原台、腾冲台、昆明台、西安台和银川台等9个台站计算的每月M2波潮汐因子整体随时间呈下降趋势。
综合图 3和4可以看出,17个台站的M2波潮汐因子的变化情况都不一样,有的呈先上升后下降的变化,有的呈先下降后上升的变化,还有的呈锯齿状的上升下降变化,无法从小的时间段分析每个台站的M2波潮汐因子的变化规律。但从整体来看,可将震前2 a的数据拟合趋势分为整体上升和整体下降,与震前1 a的数据整体拟合得到的M2波潮汐因子的变化趋势基本相同。
3.3 重力潮汐因子趋势空间变化特征通过对芦山地震前中国大陆连续重力观测台网中17个台站的数据进行分析,可以获得反映重力场动态变化的图像,不仅包含潮汐因子随时间变化的序列,还包括潮汐因子趋势变化的空间分布。图 5为芦山地震前1 a(2012-03~2013-03)及地震前2 a(2011-06~2013-03)17个台站M2波潮汐因子趋势变化的空间分布情况。

|
图 5 震前M2波潮汐因子变化空间分布 Fig. 5 Spatial distribution of tidal factor changes of M2 waves before earthquake |
为考察不同时间尺度M2波潮汐因子的趋势变化,以2个时间尺度来分析M2波潮汐因子:震前1 a(2012-03~2013-03,图 5(a))和震前2 a(2011-06~2013-03,图 5(b))。从图 5可以看出,2个时间尺度的变化趋势大体一致,局部区域存在一些差异但并不影响整体结果。在距震中300 km的范围内,M2波潮汐因子大体呈上升的趋势,根据历史震例总结,在大震前震源附近会有应力累积的过程。从整体来看,M2波潮汐因子的上升与下降变化趋势大体呈四象限分布,芦山地震位于四象限对称中心附近。
4 结语根据芦山7.0级地震的震源机制解[12],构造应力整体以逆冲型错动为主,最大主应力方向呈NW-SE。根据图 5可将震源近似看成点源,用双力偶点源模型进行分析可以看到:震源和双力偶点源模型有点偏离,这是因为离点源模型最近的断层就是震源所在区域的龙门山断裂带,与构造环境相符,震源的运动除含有剪切错动的分量以外,还有一定的单向拉伸或压缩分量,所以震源与点源模型中心存在些许偏差是合理的。比较震前(2011-06~2013-03)显示的重力潮汐因子的变化四象限分布可知,两者具有类似的分布情况。根据前人研究的震例分析可知,较大地震前震源区一般呈现相关的重力变化低值梯度带或四象限分布低值中心[13-15],这种变化特征可用震前闭锁剪力模型[16]来解释。
通过对2011~2013年芦山地震前17个重力连续观测台站的重力观测资料进行分析,可得到如下认识:
1) O1波和M2波潮汐因子变化相对稳定,除了甘孜台、姑咱台和西安台以外,M2波潮汐因子的变化均稳定在0.02‰之内,O1波潮汐因子的变化则稳定在0.6‰之内,且半日波M2波较日波O1波更稳定。
2) 分析芦山地震前17个连续重力台站近2 a(2011-06~2013-03)的M2波潮汐因子随时间的变化趋势,得到M2波潮汐因子趋势变化的空间分布情况。结果显示,其上升与下降的变化趋势大体呈四象限分布,芦山地震位于四象限对称中心附近。这种震前潮汐参数的趋势变化可能包含了更为丰富的孕震信息,可为中期、短期乃至临震的预测指标提供相关参考依据。今后将对潮汐参数时变特征与地震孕育机理的相关性进行更深入的研究分析。
| [1] |
Tanaka S, Ohtake M, Sato H. Tidal Triggering of Earthquakes in Japan Related to the Regional Tectonic Stress[J]. Earth, Planets and Space, 2004, 56(5): 511-515 DOI:10.1186/BF03352510
(  0) 0) |
| [2] |
Bonasia S. The 1976 China, Tangshan Earthquake MW=7.8 Mechanism in Retrospect[J]. Journal of Applied Sciences, 2009, 9(15): 2714-2724 DOI:10.3923/jas.2009.2714.2724
(  0) 0) |
| [3] |
吴翼麟, 牛安福, 李爱萍. 孕震区形变异常临近地震时的有序度研究[J]. 地壳形变与地震, 1993, 13(3): 7-12 (Wu Yilin, Niu Anfu, Li Aiping. Researches on Ordering of Crustal Deformation Anomalies Prior Earthquake in It's Preparation Region[J]. Crustal Deformation and Earthquake, 1993, 13(3): 7-12)
(  0) 0) |
| [4] |
薄万举, 吴翼麟. 形变、应变短临前兆标志体系[J]. 华南地震, 1996, 16(2): 20-29 (Bo Wanju, Wu Yilin. Short-Impending Precursor Index System from Crustal Deformation and Strain Data[J]. South China Journal of Seismology, 1996, 16(2): 20-29)
(  0) 0) |
| [5] |
何翔. 云龙台固体潮观测对地震监测能力的评价[J]. 高原地震, 1996, 8(4): 40-46 (He Xiang. Estimation of Solid Tide Observation for Seismologic Surveillance Ability in Yunlong Station[J]. Earthquake Research in Plateau, 1996, 8(4): 40-46)
(  0) 0) |
| [6] |
黎凯武. 日月引潮力触发地震的一个证据-论邢台、河间和唐山地震的时间特性[J]. 地震学报, 1998, 20(5): 98-104 (Li Kaiwu. Evidence from the Earthquake Triggered by the Sun and the Moon-On the Temporal Characteristics of the Xingtai, Hejian and Tangshan Earthquakes[J]. Acta Seismologica Sinica, 1998, 20(5): 98-104)
(  0) 0) |
| [7] |
沈旭章, 常千军, 梅秀苹. 兰州形变台水管倾斜仪映震能力的分析研究[J]. 西北地震学报, 2004, 26(4): 368-370 (Shen Xuzhang, Chang Qianjun, Mei Xiuping. Analysis on Precursor Effect to Earthquake of FSQ Water Tube Tilt Meter in Lanzhou Deformation Station[J]. Northwestern Seismological Journal, 2004, 26(4): 368-370)
(  0) 0) |
| [8] |
蒋骏, 张雁滨. 固体潮理论值一阶微商的解析表达式及拟合检验[J]. 地球物理学报, 1994, 37(6): 776-786 (Jiang Jun, Zhang Yanbin. A Differential Analytical-Representayion of the Theoretical Value of Earth Tide and the Fit-Testing of Earth Tide Data[J]. Chinese Journal of Geophysics, 1994, 37(6): 776-786 DOI:10.3321/j.issn:0001-5733.1994.06.009)
(  0) 0) |
| [9] |
田桂娥, 孙和平, 陈晓东. 武汉重力固体潮长周期潮汐参数的确定[J]. 大地测量与地球动力学, 2005, 25(4): 99-104 (Tian Gui'e, Sun Heping, Chen Xiaodong. Determination of Long Period Gravity Tide Parameter at Wuhan Station[J]. Journal of Geodesy and Geodynamics, 2005, 25(4): 99-104)
(  0) 0) |
| [10] |
孙和平, 徐建桥, 崔小明. 重力场的地球动力学与内部结构应用研究进展[J]. 测绘学报, 2017, 46(10): 1290-1299 (Sun Heping, Xu Jianqiao, Cui Xiaoming. Research Progress of the Gravity Field Application in Earth's Geodynamics and Interior Stucture[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1290-1299 DOI:10.11947/j.AGCS.2017.20170298)
(  0) 0) |
| [11] |
Melchior P, 方俊, Ducarme B, 等. 中国固体潮观测研究[J]. 地球物理学报, 1985, 28(2): 142-154 (Melchior P, Fang Jun, Ducarme B, et al. Studies on the Earth Tide Observations in China[J]. Acta Geophysica Sinica, 1985, 28(2): 142-154 DOI:10.3321/j.issn:0001-5733.1985.02.004)
(  0) 0) |
| [12] |
刘杰, 易桂喜, 张致伟, 等. 2013年4月20日四川芦山M7.0级地震介绍[J]. 地球物理学报, 2013, 56(4): 1404-1407 (Liu Jie, Yi Guixi, Zhang Zhiwei, et al. Introduction to the Lushan, Sichuan M7.0 Earthquake on 20 April 2013[J]. Chinese Journal of Geophysics, 2013, 56(4): 1404-1407)
(  0) 0) |
| [13] |
吴国华, 罗增雄, 赖群. 丽江7.0级地震前后滇西实验场的重力异常变化特征[J]. 地震研究, 1997, 20(1): 103-109 (Wu Guohua, Luo Zengxiong, Lai Qun. The Variation Characteristics of Gravity Anomaly in the Earthquake Prediction Test Site in Western Yunnan before and after the M7.0 Lijiang Earthquake[J]. Journal of Seismological Research, 1997, 20(1): 103-109)
(  0) 0) |
| [14] |
申重阳, 李辉, 孙少安, 等. 2008年于田MS7.3地震前重力场动态变化特征分析[J]. 大地测量与地球动力学, 2008, 30(4): 1-7 (Shen Chongyang, Li Hui, Sun Shao'an, et al. . Characteristic Analysis of Dynamic Gravity Change before Yutian MS7.3 Earthquake, 2008[J]. Journal of Geodesy and Geodynamics, 2008, 30(4): 1-7)
(  0) 0) |
| [15] |
申重阳, 李辉, 谈洪波, 等. 2009年姚安MS6.0地震重力场前兆变化机理[J]. 大地测量与地球动力学, 2011, 31(2): 17-22 (Shen Chongyang, Li Hui, Tan Hongbo, et al. Mechanism of Precursory Gravity Change before Yao'an MS6.0 Earthquake in 2009[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 17-22)
(  0) 0) |
| [16] |
郝洪涛, 李辉, 胡敏章, 等. 芦山地震科学考察观测到的重力变化[J]. 大地测量与地球动力学, 2015, 35(2): 331-335 (Hao Hongtao, Li Hui, Hu Minzhang, et al. Gravity Varition Observed by Scientific Expedition of Lushan Earthquake[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 331-335)
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 40
2019, Vol. 40


