2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙市麓山南路932号, 410083
由于测量数据在获取过程中受环境、仪器、人为及认识不足等因素影响,往往会存在不确定性,这种不确定性是一种广义的误差,是不精确性、模糊性及不明确性等概念的总称,既包含偶然误差等可以数值化的误差,也包含一些无法度量的误差。在很多情况下,这种不确定性无法用具体数值来表达,而是在一定的实数区间或一定范围内变动,有时也仅是一个模糊数,给后续的数据处理带来很大影响[1-3]。在测量数据处理领域,如何对测量数据的不确定性进行处理已经成为一个研究热点[2-10],但目前已有的不确定性平差模型和算法主要是针对系数矩阵和观测向量的不确定性,未考虑参数本身的有界不确定性,即未考虑参数的不等式约束[11-14]。针对这个问题,本文将基于2-范数的不确定性平差模型和参数的不等式约束相结合,建立有界不确定性平差模型,并从等式约束出发,利用无限权和零权思想,提出一种简单直接且能快速收敛的有界不确定性平差迭代算法(least square with uncertain and inequality constraints,ICULS)。
1 有界不确定性平差模型基于2-范数的不确定性平差模型为:
| $ \left\{\begin{array}{l} {\boldsymbol{L}+\Delta \boldsymbol{L}=(\boldsymbol{A}+\Delta \boldsymbol{A}) \boldsymbol{X}} \\ {\|\Delta \boldsymbol{A}\|_{2} \leqslant \alpha} \\ {\|\Delta \boldsymbol{L}\|_{2} \leqslant \beta} \end{array}\right. $ | (1) |
式中,A为m×n(m≥n)维设计矩阵,L为n维观测向量,ΔA =[aij]m×n为A的不确定性,ΔL=[Δl1 Δl2 … Δlm]T为L的不确定性,不确定度α和β以2-范数的形式来描述这两种不确定性[2]。
从式(1)可以看出,不确定性平差模型将系数矩阵中的不确定性以不确定度α的形式纳入平差模型,如果进一步考虑参数的不确定性,增加参数的不等式约束,则可以建立有界不确定性平差模型:
| $ \left\{\begin{array}{l} {\boldsymbol{L}+\Delta \boldsymbol{L}=(\boldsymbol{A}+\Delta \boldsymbol{A}) \boldsymbol{X}} \\ {\|\Delta \boldsymbol{A}\|_{2} \leqslant \alpha} \\ {\|\Delta \boldsymbol{L}\|_{2} \leqslant \beta} \\ {\boldsymbol{G} \boldsymbol{X} \leqslant \boldsymbol{W}} \end{array}\right. $ | (2) |
式中,G为s×n维的约束矩阵,W为与之对应的s维常数向量。有界不确定性平差模型是对参数附加不等式约束的不确定性平差模型,为了计算最后的参数估计,可以先考虑参数附等式约束的不确定性平差模型:
| $ \left\{\begin{array}{l} {\boldsymbol{L}+\Delta \boldsymbol{L}=(\boldsymbol{A}+\Delta \boldsymbol{A}) X} \\ {\|\Delta \boldsymbol{A}\|_{2} \leqslant \alpha} \\ {\|\Delta \boldsymbol{L}\|_{2} \leqslant \beta} \\ {\boldsymbol{C} \boldsymbol{X}=\boldsymbol{b}} \end{array}\right. $ | (3) |
式中,C为s2×n维的约束矩阵,b为与之对应的s2维常数向量。
2 附等式约束的不确定性平差模型解算方法对于基于2-范数的不确定性平差模型,文献[2]建立如下不确定性min-max平差准则:
| $ \min _{X} \max\limits_{\|\Delta \boldsymbol{A}\|_{2} \leqslant \boldsymbol{\alpha}, \|\Delta \boldsymbol{L}\|_{2} \leqslant \beta}\left\{\|(\boldsymbol{L}+\Delta \boldsymbol{L})-(\boldsymbol{A}+\Delta \boldsymbol{A}) \boldsymbol{X}\|_{2}\right\} $ | (4) |
根据范数的性质可以推导出,当且仅当
| $ \Delta \boldsymbol{A}=\frac{\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}} \frac{\boldsymbol{X}^{\mathrm{T}}}{\|\boldsymbol{X}\|_{2}}{\alpha} $ | (5) |
| $ \Delta \boldsymbol{L}=\frac{\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}} \beta $ | (6) |
时,不确定性min-max平差准则可以转化为更简单的min平差准则:
| $ \min _{X}\left\{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}+\alpha\|\boldsymbol{X}\|_{2}+\beta\right\} $ | (7) |
对于参数附等式约束的不确定性平差模型(式(3)),由于不确定性平差模型的min-max平差准则是以范数形式表现的,因此可以将等式约束化为相同的范数形式,建立目标函数:
| $ f(\boldsymbol{X}, \lambda) =\|\boldsymbol{A X}-\boldsymbol{L}\|_{2}+\\ \alpha\|\boldsymbol{X}\|_{2}+\beta+\lambda\|\boldsymbol{C X}-\boldsymbol{b}\|_{2} $ | (8) |
由于不确定性平差模型的解是迭代得出的,存在限差,因此‖ CX - b ‖2不断接近于0但不能完全等于0。对X求偏导,得到:
| $ \frac{\partial f(\boldsymbol{X}, \lambda)}{\partial \boldsymbol{X}}=\frac{\boldsymbol{A}^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L})}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}+\frac{\alpha \boldsymbol{X}}{\|\boldsymbol{X}\|_{2}}+\frac{\lambda \boldsymbol{C}^{\mathrm{T}}(\boldsymbol{C} \boldsymbol{X}-\boldsymbol{b})}{\|\boldsymbol{C} \boldsymbol{X}-\boldsymbol{b}\|_{2}}=\\\frac{1}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}\left(\boldsymbol{A}^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L})+\frac{\alpha\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2} \boldsymbol{X}}{\|\boldsymbol{X}\|_{2}}+\right.\\ \left.\frac{\lambda\|\boldsymbol{A X-L}\|_{2} \boldsymbol{C}^{\mathrm{T}}(\boldsymbol{C X}-\boldsymbol{b})}{\|\boldsymbol{C X}-\boldsymbol{b}\|_{2}}\right)=\frac{1}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}\\\left(\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\frac{\alpha\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}{\|\boldsymbol{X}\|_{2}} \boldsymbol{I}+\frac{\lambda\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}{\|\boldsymbol{C X}-\boldsymbol{b}\|_{2}} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C}\right) \boldsymbol{X}-\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}-\right.\\\left.\frac{\lambda\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{b}}{\|\boldsymbol{C} \boldsymbol{X}-\boldsymbol{b}\|_{2}}\right)=\frac{1}{\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{L}\|_{2}}\\\left(\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu \boldsymbol{I}+\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C}\right) \boldsymbol{X}-\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}-\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{b}\right) $ | (9) |
其中,
| $ \left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu \boldsymbol{I}+\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C}\right) \boldsymbol{X}-\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}-\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{b}=0 $ | (10) |
则:
| $ \hat{\boldsymbol{X}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu \boldsymbol{I}+\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}+\rho \boldsymbol{C}^{\mathrm{T}} \boldsymbol{b}\right) $ | (11) |
式(11)为参数的形式解,等式左右两边都有未知参数解,则可以通过迭代得到附等式约束的不确定性平差模型的参数估计
如果将ρ纳入到权矩阵中,则式(11)可转变为:
| $ \hat{\boldsymbol{X}}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu \boldsymbol{I}+\boldsymbol{C}^{\mathrm{T}} \boldsymbol{P}^{\prime} \boldsymbol{C}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}+\boldsymbol{C}^{\mathrm{T}} \boldsymbol{P}^{\prime} \boldsymbol{b}\right) $ | (12) |
其中,P′ =ρ I,ρ也可以直接取一个较大的数,如ρ=106。从形式上看,式(12)是利用无限权的思想来处理等式约束,对于不等式约束则可以进一步结合零权的思想来处理[11]。令
| $ \boldsymbol{V}^{\prime}=\boldsymbol{G} \boldsymbol{X}-\boldsymbol{W} $ | (13) |
在迭代过程中,V′i≤0时为不等式约束满足,V′ i>0时为不等式约束不满足。分别对这两种情况进行定权:
| $ \boldsymbol{P}_{i}^{\prime}=\left\{\begin{array}{l} {\rho, \boldsymbol{V}_{i}^{\prime}>0} \\ {0, \boldsymbol{V}_{i}^{\prime} \leqslant 0} \end{array}\right. $ | (14) |
即当不等式约束满足时,为无效约束,P′ i=0;当不等式约束不满足时,为有效约束,P′ i=ρ可取一个较大的值,如ρ=106。与附等式约束的不确定性平差模型的参数估计类似,有界不确定性平差模型的参数估计也是利用迭代得到的。由基于2-范数的不确定性平差算法的收敛性质可知,当α很小时,有界不确定性迭代算法是收敛的,且由于系数矩阵的不确定度α是一个很小的数,因此有界不确定性迭代算法一般是收敛的。具体算法步骤为:
1) 给定初始值
2) 计算μk和权矩阵P′的值:
| $ \begin{aligned} \mu_{k}=& \frac{\alpha\left\|\boldsymbol{A} \hat{\boldsymbol{X}}_{k-1}-\boldsymbol{L}\right\|_{2}}{\left\|\hat{\boldsymbol{X}}_{k-1}\right\|_{2}} \\ \boldsymbol{P}_{i}^{\prime}=&\left\{\begin{array}{l} {\rho, \boldsymbol{V}_{i}^{\prime}>0} \\ {0, \boldsymbol{V}_{i}^{\prime} \leqslant 0} \end{array}\right. \end{aligned} $ |
3) 计算
| $ \hat{\boldsymbol{X}}_{k}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\mu_{k} \boldsymbol{I}+\boldsymbol{G}^{\mathrm{T}} \boldsymbol{P}^{\prime} \boldsymbol{G}\right)^{-1}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}+\boldsymbol{G}^{\mathrm{T}} \boldsymbol{P}^{\prime} \boldsymbol{W}\right) $ |
4) 如果
为验证本文算法的可行性和有效性,对文献[14]中的不等式约束算例进行改化,系数矩阵A中添加了随机误差vec(ΔA)~N(0, σ12 Im⊗In), σ1=0.005,不考虑不等式约束条件的参数真值为
|
|
表 1 不等式约束算例 Tab. 1 An example of inequality constraint |
分别用LS、ICLS(附不等式约束平差算法[11])、ICTLS(附不等式约束的总体最小二乘法[15])及本文提出的ICULS(已知ΔA的不确定度α=norm(ΔA)=0.015 8,在平差过程中β不参与计算,因此忽略不计)对改化后的不等式约束算例进行处理,具体结果见表 2,其中参数估值与真实值之间的残差范数为
|
|
表 2 算例的算法结果与比较 Tab. 2 The algorithm results and comparison of example |
从表 2可以看出,在不确定度α已知的前提下,ICULS的残差范数小于ICLS和ICTLS,即ICULS的结果更接近真值。这进一步说明,在不确定度可靠的前提下,本文提出的算法是可行、有效的。另外,如图 1所示,除了LS不考虑不等式约束对参数的影响,ICLS、ICTLS及ICULS最后得出的有效约束均为第2、第8及第9个不等式约束,说明本文提出的方法对解决参数有界不确定性平差问题是有效的。图 2显示了ICULS的残差范数m与不确定度α的关系,可以看出,不确定度α在一定的区间范围内是可靠的。
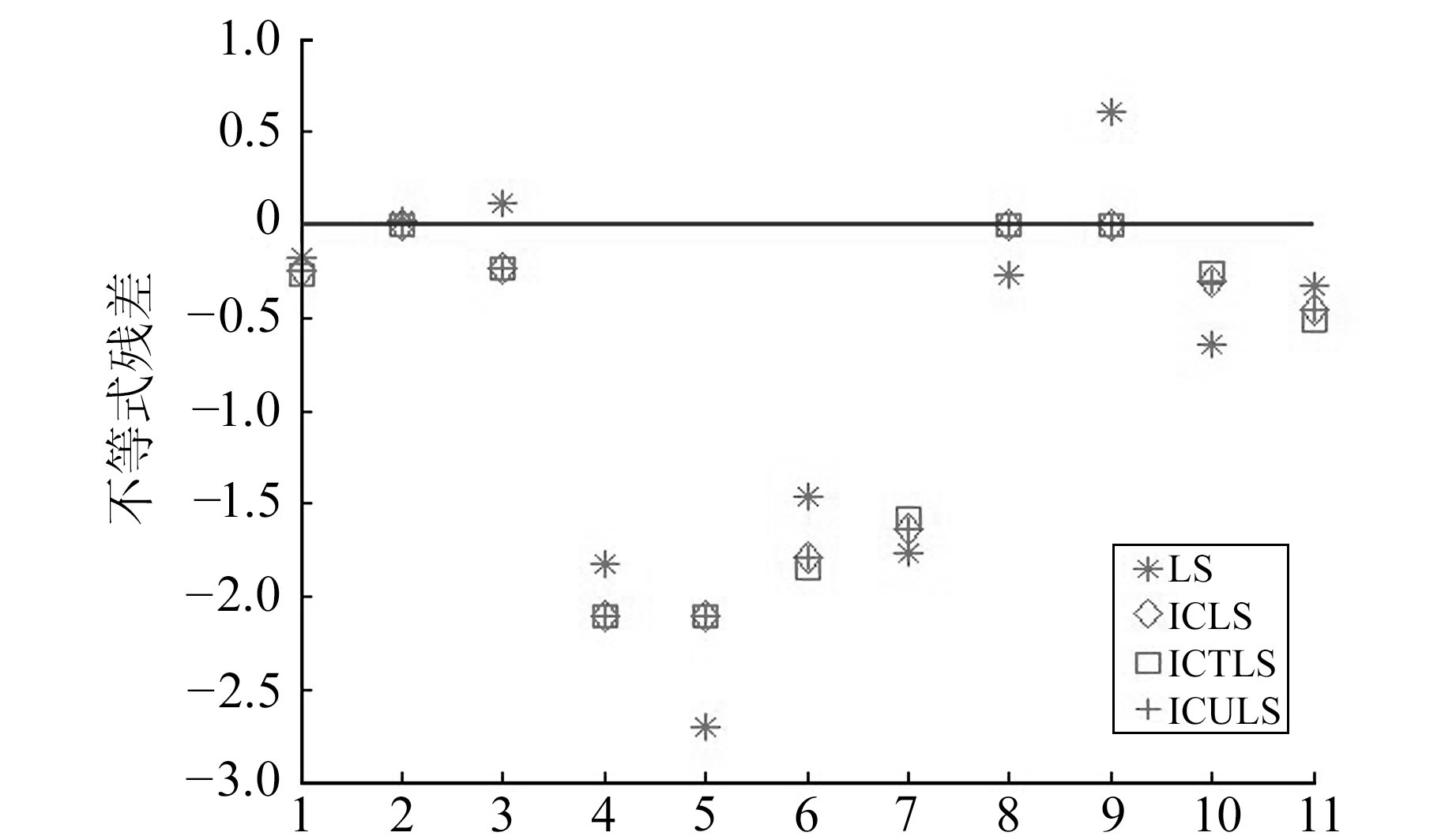
|
图 1 不等式残差 Fig. 1 Residual error of inequality constraints |
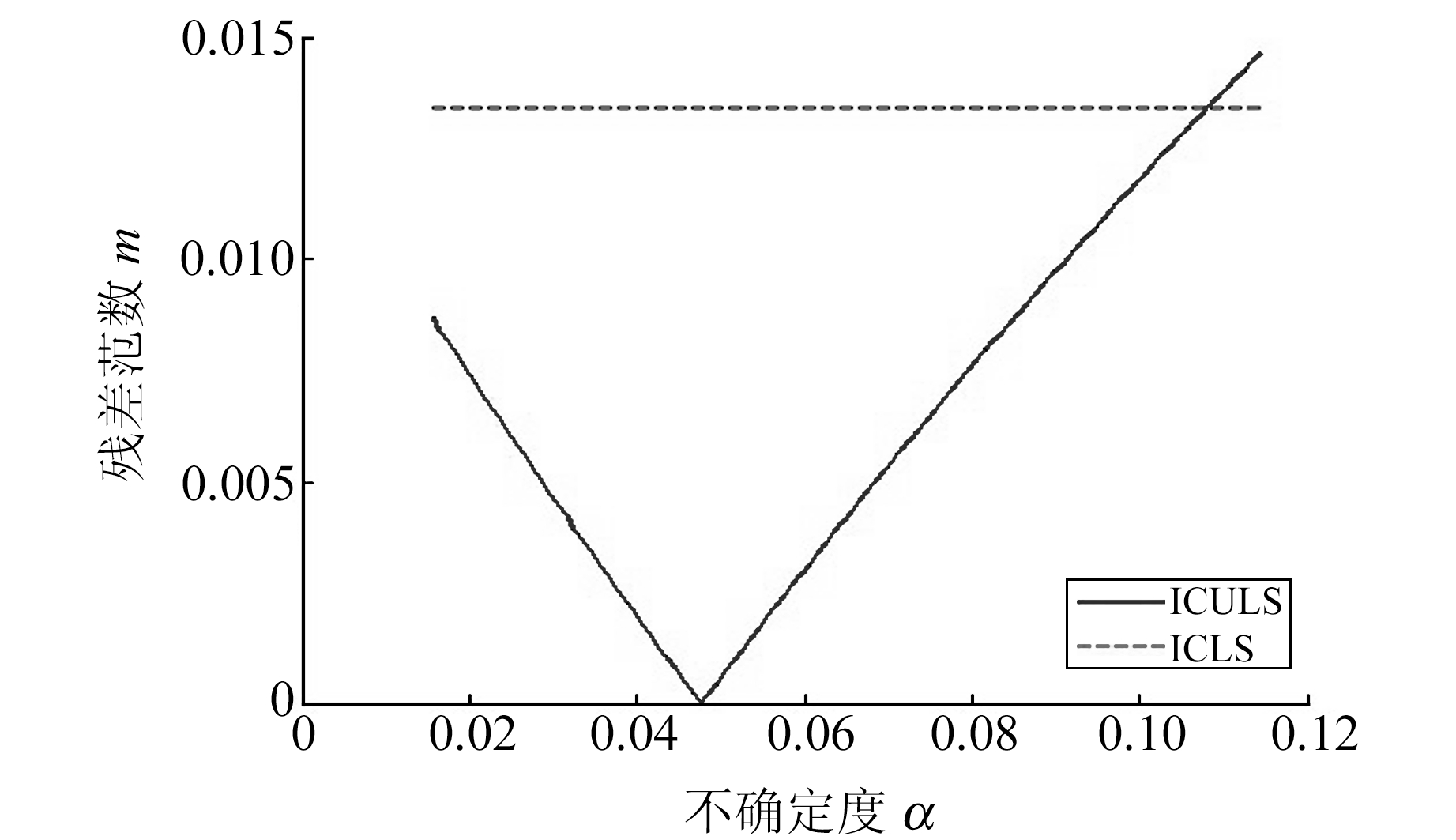
|
图 2 ICULS的残差范数变化 Fig. 2 Variation in residual norm of ICULS |
为了比较ICULS的收敛速度,保持真值及不确定度α不变,每次加入不同的随机误差,独立重复运行10 000次,统计得到ICULS的平均迭代次数为10.067 1。而ICTLS是利用穷举法得到有效约束的,其迭代次数远大于ICULS,由此说明ICULS的迭代次数少、收敛速度快。
5 结语不确定性平差模型主要考虑系数矩阵和观测向量的不确定性,但实际中也存在大量关于参数的先验信息或附加信息,根据这些信息可以建立附不等式约束的平差模型,即参数自身的有界不确定性。针对这种参数的有界不确定性及不确定性平差模型,本文建立了有界不确定性平差模型,并结合不等式约束中无限权和零权的思想提出有界不确定性平差迭代算法。该算法简单可行,可同时估计系数矩阵、观测向量及参数自身的有界不确定性,在不确定度可靠的前提下能快速收敛。
| [1] |
杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650 (Yang Yuanxi. Some Note on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650)
(  0) 0) |
| [2] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141 (Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Ceriterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135-141)
(  0) 0) |
| [3] |
Chandrasekaran S, Golub G H, Gu M, et al. Parameter Estimation in the Presence of Bounded Data Uncertainties[J]. SIAM Journal on Matrix Analysis and Applications, 1998, 19(1): 235-252 DOI:10.1137/S0895479896301674
(  0) 0) |
| [4] |
鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉: 武汉大学, 2010 (Lu Tieding. Research on Total Least Squares and Its Applications in Surveying Data Processing[D]. Wuhan: Wuhan University, 2010) http://www.cnki.com.cn/Article/CJFDTotal-CHXB201304028.htm
(  0) 0) |
| [5] |
Schaffrin B, Lee I, Choi Y, et al. Total Least-Squares (TLS) for Geodetic Straight-Line and Plane Adjustment[J]. Bollettino di Geodesia e Scienze Affini, 2006, 65(3): 141-168
(  0) 0) |
| [6] |
Neitzel F. Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762 DOI:10.1007/s00190-010-0408-0
(  0) 0) |
| [7] |
宋迎春, 金昊, 崔先强. 带有不确定性的观测数据平差解算方法[J]. 武汉大学学报:信息科学版, 2014, 39(7): 788-792 (Song Yingchun, Jin Hao, Cui Xianqiang. Adjustment Algorithm about Observation Data with Uncertain[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788-792)
(  0) 0) |
| [8] |
朱国红, 鲁铁定. 有界不确定性平差模型的迭代算法[J]. 测绘科学, 2017, 42(6): 41-45 (Zhu Guohong, Lu Tieding. Iterative Algorithm for Adjustment Model with Bounded Data Uncertainties[J]. Science of Surveying and Mapping, 2017, 42(6): 41-45)
(  0) 0) |
| [9] |
王志忠, 陈丹华, 宋迎春. 具有不确定性平差算法[J]. 测绘学报, 2017, 46(7): 834-840 (Wang Zhizhong, Chen Danhua, Song Yingchun. An Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 834-840)
(  0) 0) |
| [10] |
王志忠, 宋迎春, 何玲莉. 系数矩阵中部分有界不确定性的混合平差算法[J]. 测绘学报, 2018, 47(9): 1171-1178 (Wang Zhizhong, Song Yingchun, He Lingli. Mixed Adjustment Algorithm for Part of the Coefficient Matrix with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(9): 1171-1178)
(  0) 0) |
| [11] |
朱建军, 谢建. 附不等式约束平差的一种简单迭代算法[J]. 测绘学报, 2011, 40(2): 209-212 (Zhu Jianjun, Xie Jian. A Simple Iterative Algorithm for Inequality Constrained Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 209-212)
(  0) 0) |
| [12] |
冯光财, 朱建军, 陈正阳, 等. 基于有效约束的附不等式约束平差的一种新算法[J]. 测绘学报, 2007, 36(2): 119-123 (Feng Guangcai, Zhu Jianjun, Chen Zhengyang, et al. A New Approach to Inequality Constrained Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 119-123 DOI:10.3321/j.issn:1001-1595.2007.02.001)
(  0) 0) |
| [13] |
Zhu J, Santerre R, Chang X W. A Bayesian Method for Linear Inequality Constrained Adjustment and Its Application to GPS Positioning[J]. Journal of Geodesy, 2005, 78(9): 528-534 DOI:10.1007/s00190-004-0425-y
(  0) 0) |
| [14] |
Peng J H, Zhang H P, Shong S, et al. An Aggregate Constraint Method for Inequality-Constrained Least Squares Problems[J]. Journal of Geodesy, 2006, 79(12): 705-713 DOI:10.1007/s00190-006-0026-z
(  0) 0) |
| [15] |
Zhang S L, Tong X H, Zhang K. A Solution to EIV Model with Inequality Constraints and Its Geodetic Applications[J]. Journal of Geodesy, 2013, 87(1): 23-28
(  0) 0) |
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, 932 South-Lushan Road, Changsha 410083, China
 2020, Vol. 40
2020, Vol. 40

