水库的水位状态是大坝安全运行的重要因素之一。通常情况下,水库会建立标志进行水位数据的读取,但该方法效率低、浪费人力、出错率高,因此,如何有效地获取水库长期稳定的水位数据至关重要[1]。过去,由多路径效应引起的GNSS-MR(global navigation satellite system multipath reflectometry)信号被广泛应用于雪深变化、海平面变化及土壤湿度探测等研究领域[2-10]。近年来,将基于多路径效应的GNSS-MR技术应用于地表环境监测已成为一种新兴的遥感手段[11],利用这种新的大坝水位估计方法可实现水位读取的自动化、准确化,并能极大地提高GNSS数据的利用率,节约水位观测成本,对于大坝、湖泊等水位监测具有重要意义。
GNSS接收机所安置的观测环境对GNSS-MR的研究非常重要。以水电站为例,天线周边的复杂环境使得水面反射信号难以分离,有效提取SNR中的水面反射成分具有很大的挑战性。为解决该问题,本文通过分析信号频率、高度角范围、弧段长度等因素对水位估计结果的影响,结合大坝的实际观测情况,确定相应的约束条件,最终实现大坝的水位变化监测,并将获取的水位结果与实测水位数据进行对比分析,验证该技术的适用性及有效性。
1 GNSS-MR模型模型的建立基于GNSS直射信号和反射信号之间的干扰在SNR数据中产生的特征变化,而该特征变化取决于接收机天线与反射表面之间的距离。图 1为大坝水面反射的示意图。

|
图 1 大坝水面反射示意图 Fig. 1 Dam surface reflection geometry |
由图 1可知,GNSS天线接收了直射信号和来自水面的反射信号,h为接收机天线到水面的距离,θ为信号与水面的夹角,HG和HW分别为接收机天线和水面到水准面的距离。理想情况下,接收机只接收来自卫星的直射信号,但实际上接收机接收的是直射信号与来自卫星信号经过一个或多个反射物反射的反射信号产生干涉后的混合信号,即多路径效应。由于经过多余的路径产生附加的时间延迟,偏离真实卫星信号,从而产生误差,因此反射的相位延迟为:
| $ \psi=\frac{2 \pi}{\lambda} 2 h \sin \theta $ | (1) |
式中,ψ为由路径延迟引起的相位延迟(相位差),λ为信号载波波长。根据式(1)可以获得ψ随时间变化的角频率为:
| $ \omega_{m}=\frac{\mathrm{d} \psi}{\mathrm{d} t}=\frac{4 \pi}{\lambda} h \cos \theta \frac{\mathrm{d} \theta}{\mathrm{d} t} $ | (2) |
式(2)可转换为:
| $ \frac{\mathrm{d} \psi}{\mathrm{d} \sin \theta}=\frac{4 \pi}{\lambda} h $ | (3) |
通过式(3)可以看出,相对相位ψ与sinθ之间存在线性关系。由于SNR观测值与相对相位ψ之间是余弦的关系,除去直射信号的多路径分量dSNR与sinθ之间可以用某一固定频率(天线相位中心至反射物的垂直距离一定)的正弦或者余弦函数来表示:
| $ \mathrm{d} \mathrm{SNR}_{\mathrm{MP}}=A_{\mathrm{MP}} \cos \left(\frac{4 \pi H_{0}}{\lambda} \sin \theta+\varphi_{\mathrm{MP}}\right) $ | (4) |
式中,H0为天线相位中心至反射物的垂直距离,AMP为dSNR中反射信号的振幅,φMP为dSNR中反射信号的相位。其中,H0采用L-S频谱分析的方法获得,即对长时间非均匀采样的观测数据进行频谱分析[12],该分析方法将返回振幅和频率信号,通过获取的主频信号将频率转换为有效反射高度,即
| $ f_{m}=\frac{2 H_{R}}{\lambda} $ | (5) |
式中,fm为L-S频谱分析的主频率,HR为有效反射高度。
为确保测站反射信号完全落在水面上,避免来自陆地的反射信号对反演结果造成影响,需进行菲涅尔反射区分析,菲涅耳带反映了卫星反射信号的反射轨迹。菲涅尔反射区与水面高度和卫星高度角有关,随着水位的升高,菲涅尔带逐渐变小并向测站方向靠拢;随着卫星高度角的降低,菲涅尔带逐渐延伸。根据这些因素并结合水面位置的分布,确保测站反射信号完全落在水面上。
2 实验数据在某大坝设计了GNSS-MR实验,使用的接收机类型为北斗星通M6200,天线类型为A6000,采样率为5 s,高度角设为0°,采样时段为2017年年积日174~249(2017-06-23~09-06),采集的数据为GPS的L1和L2及BDS的B1和B2的信噪比观测值,其中包含GPS的G01~G32共32颗MEO卫星及BDS的C02~C05共4颗GEO卫星、C06~C10共5颗IGSO卫星和C11~C14共4颗MEO卫星。由于受大坝环境遮挡的影响,SNR数据的最低高度角为20°左右,水面距离天线高度大约8 m,依此确定的水面反射区域是半径约为30 m、方位角为190°~350°的扇形区域,从而保证接收机接受的信号为水面的反射信号。实验期间每天同时实测一个水位数据,用于检验GNSS-MR的水位反演结果。图 2为布设在大坝顶部的一个接收机天线。

|
图 2 GNSS接收机天线安装位置 Fig. 2 GNSS receiver antenna mounting position |
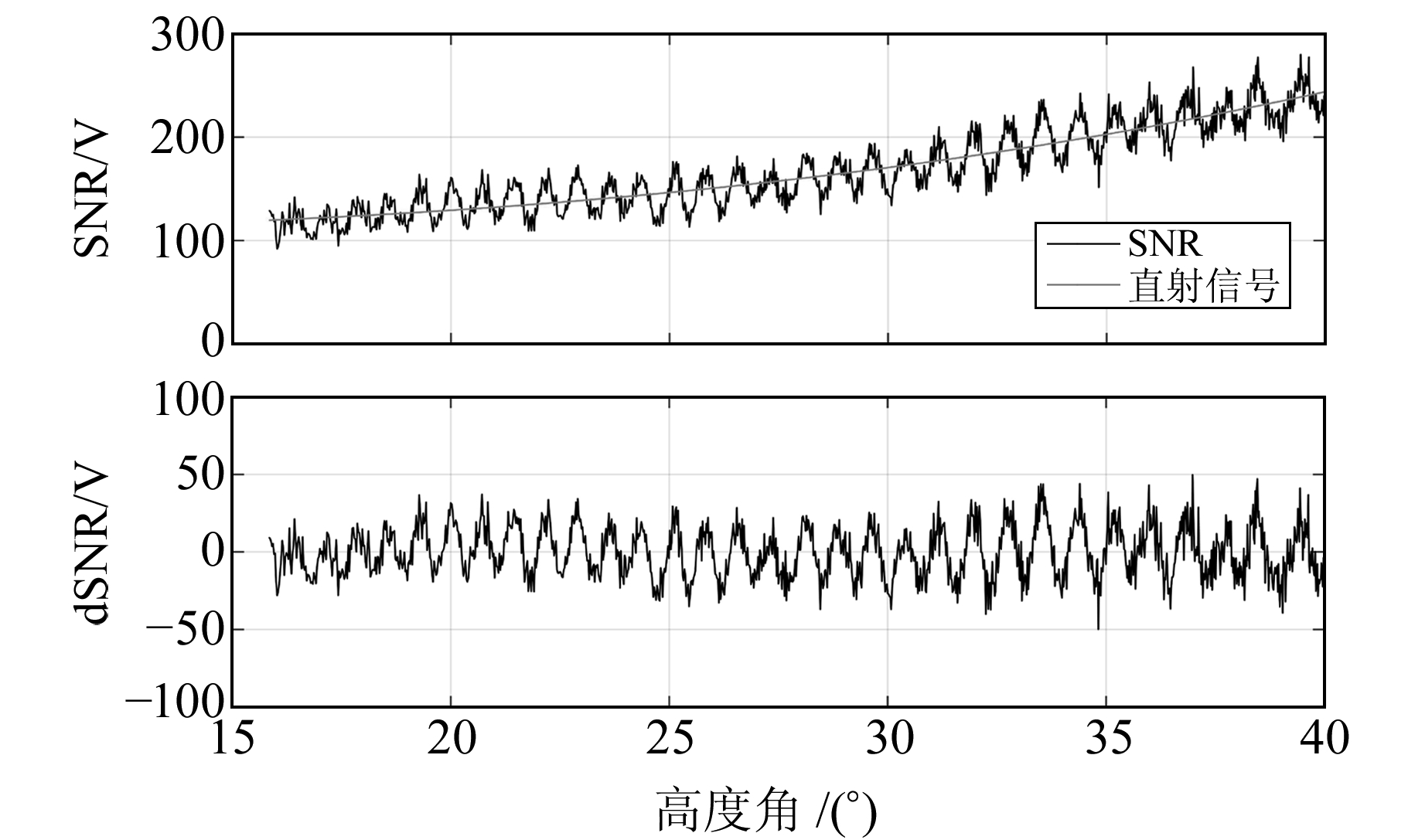
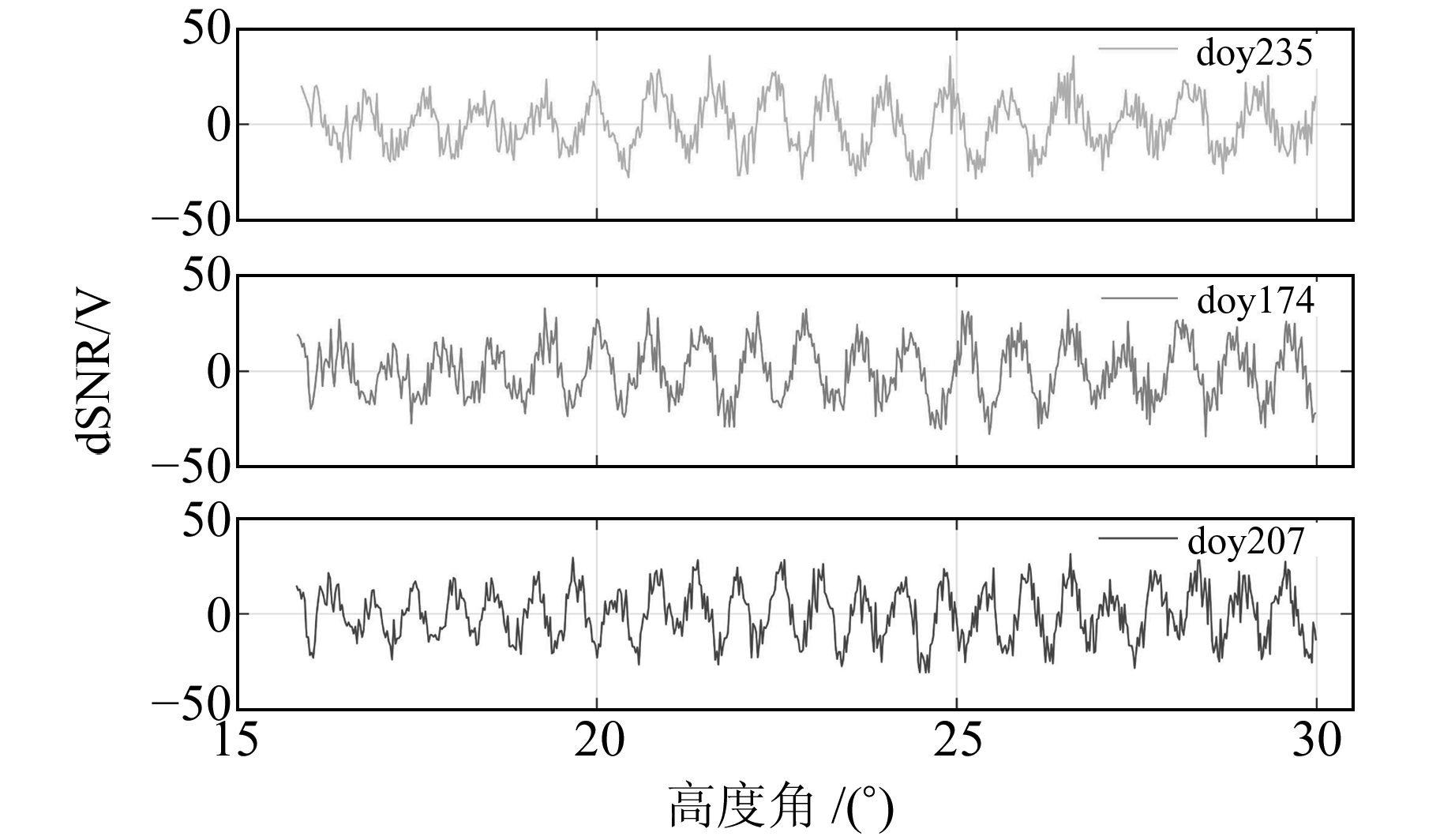
以GPS的G19卫星为例进行直射信号与反射信号的分离及重采样,直射信号主要表现为SNR数据大的趋势项,可通过多项式拟合的方式去除。图 3为G19卫星线性单位化后的SNR数据和去除直射信号的dSNR数据。去除直射信号的G19卫星的多路径分量与卫星高度角之间存在着正弦函数关系,根据式(4)所示的dSNR与高度角正弦sinθ之间的关系式建立函数模型,采用L-S频谱分析方法对年积日174、207和235的dSNR序列进行频谱分析(图 4),将结果分别代入式(5),得到的有效反射高度结果见图 5。
|
图 3 G19卫星L1的SNR结果 Fig. 3 Result of dSNR of G19 L1 |
|
图 4 G19卫星L1年积日174、207和235的dSNR Fig. 4 G19L1 dSNR for doy 174, 207, 235 |
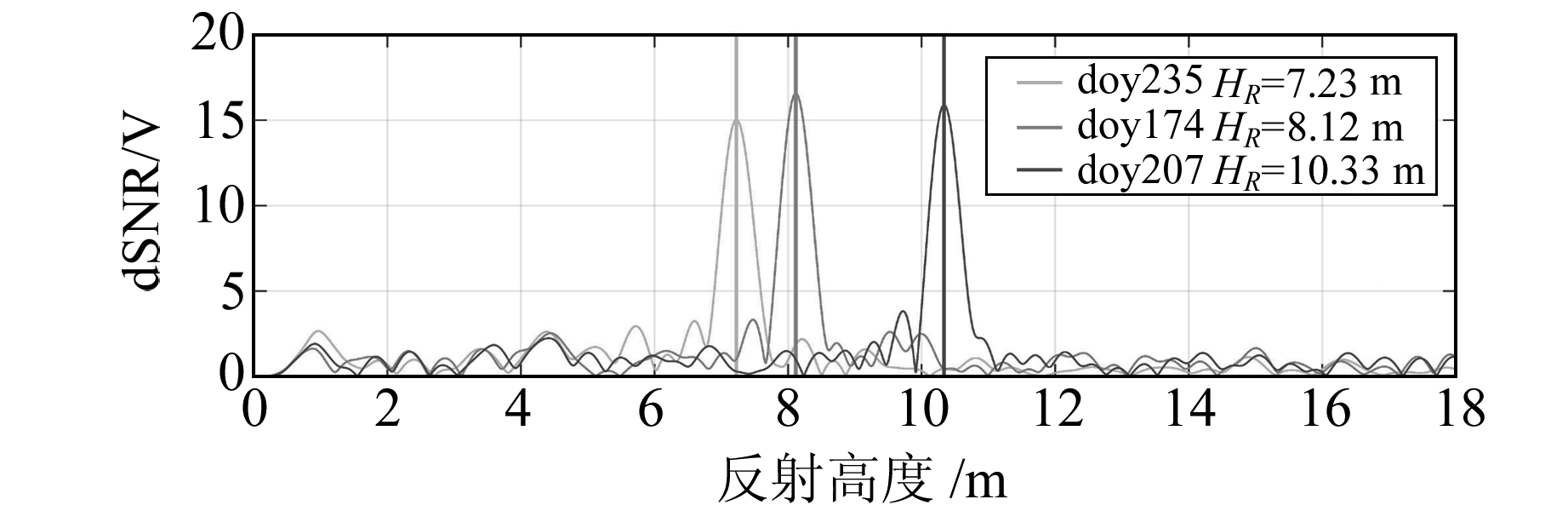
从图 5可以看出,因水面高度的不同,3个序列显示出明显而独特的主频率,可有效地反映水面变化。
|
图 5 G19卫星L1年积日174、207、235的有效反射高度 Fig. 5 G19 L1 HR for doy 174, 207, 235 |
利用SNR数据进行水位反演的方法并不能完全刻画大坝的实际情况,受观测环境的影响,为获取可靠的水位结果必须对卫星导航系统的SNR数据质量进行评估,并选择合适的SNR数据。
3.1 卫星信号频率图 6为2017年年积日204~235期间GPS和BDS所有卫星2种频率之间的水位反演结果与实测水位的中误差结果对比,图中横轴为卫星号,纵轴为中误差,其中缺失的部分代表L2(B2)频率无法完成反演。

|
图 6 2种频率反演结果的中误差对比 Fig. 6 Median error comparison of two frequency inversion results |
由图 6(a)可知,GPS的G9、G7和G21卫星的L1频率可以成功进行水位反演,而L2频率则反演失败,而2种频率都可以反演的其余GPS卫星中,L1频率的反演精度普遍高于L2频率,且较为平稳。表 1统计了2017年年积日174的不同频率所有卫星频谱分析获取的振幅平均值和有效反射高度,由表可知,各个频率反演的高度基本一致,但振幅平均值较低,而振幅与信噪比的大小有关,说明反演精度与卫星信号的载波频率关系不大,主要与信噪比的大小有关,信噪较小会导致反演精度较低,且会进一步导致图 6(a)中某些卫星的L2频率反演失败。
|
|
表 1 年积日174的GPS与BDS水位反演结果 Tab. 1 Result of doy 174 GPS and BDS water level retrieval |
对于BDS,在利用SNR数据进行水位反演时需要依靠高度角的变化来进行频谱分析,因此在天空相对位置固定不动的GEO地球同步卫星无法进行水位反演。图 6(b)为BDS的IGSO卫星和MEO卫星2种频率反演结果的中误差对比,如图所示,B1与B2频率的SNR数据反演精度无显著差异,但也存在B2频率反演失败的情况。事实上C9和C13卫星2种频率之间的反演数据在年积日204~235期间均出现了多天反演失败的情况,只不过B1频率表现稍好一些,反演了大部分数据,所以这里作了保留;而B2频率数据缺失严重,这里没有绘出。值得一提的是,C9为IGSO卫星,高度角变化很小,相较于MEO卫星反演精度更低,也进一步出现SNR反演频繁失败的情况。
由此可知,基于L1和B1频率的水位反演成功率和精度更高,选取利用L1和B1频率更有利于进行大坝的水位反演。
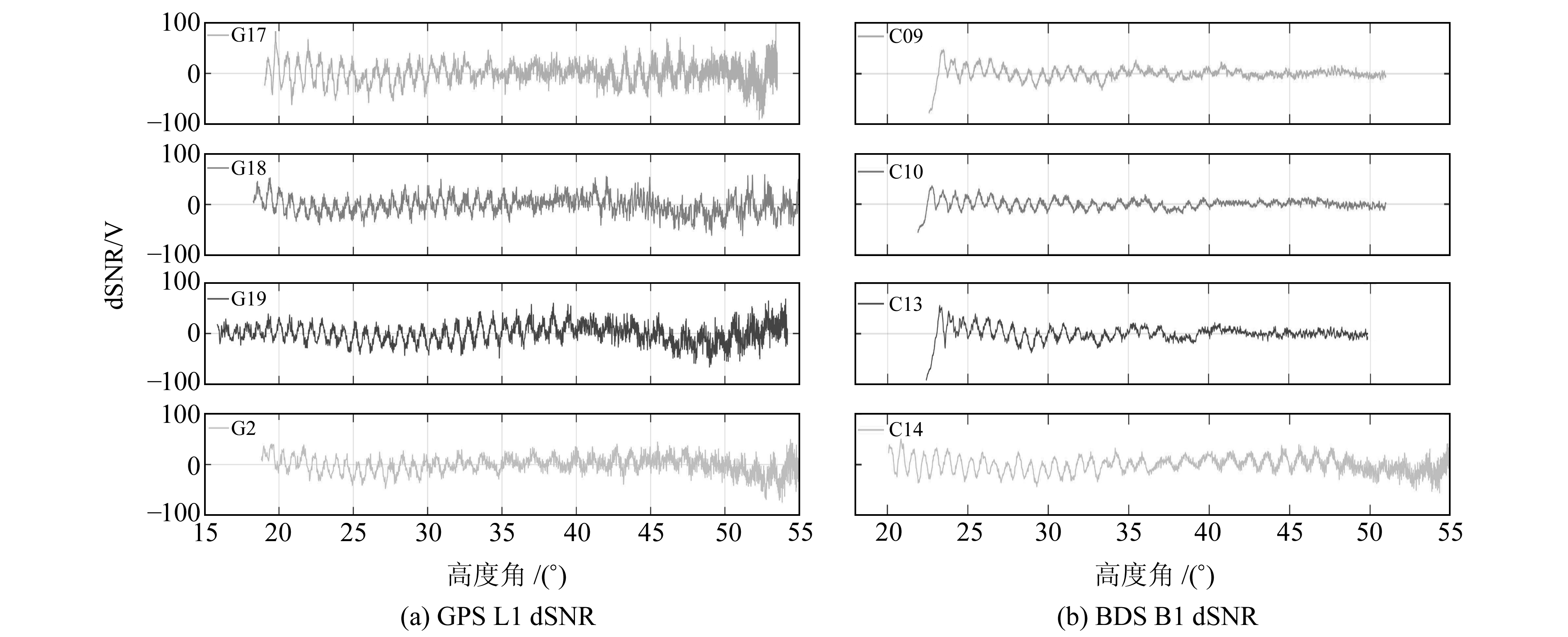
3.2 卫星高度角图 7为从GPS的L1频率和BDS的B1频率各选取4颗卫星、显示高度角在0°~55°的dSNR序列,由图可知,dSNR在高度角大约35°以下时具有更明显的波动,显示出特征频率;随着卫星高度角的增加,信号将逐渐变得混叠;当卫星高度角较大时,由于多路径效应微弱,dSNR序列已经不能很好地显示正弦特征,无法得到较好的反演结果。因此,选取高度角在35°以下的数据信号区分更为明显,更有利于dSNR数据的频谱分析。
|
图 7 卫星的dSNR序列 Fig. 7 dSNR sequences for satellites |
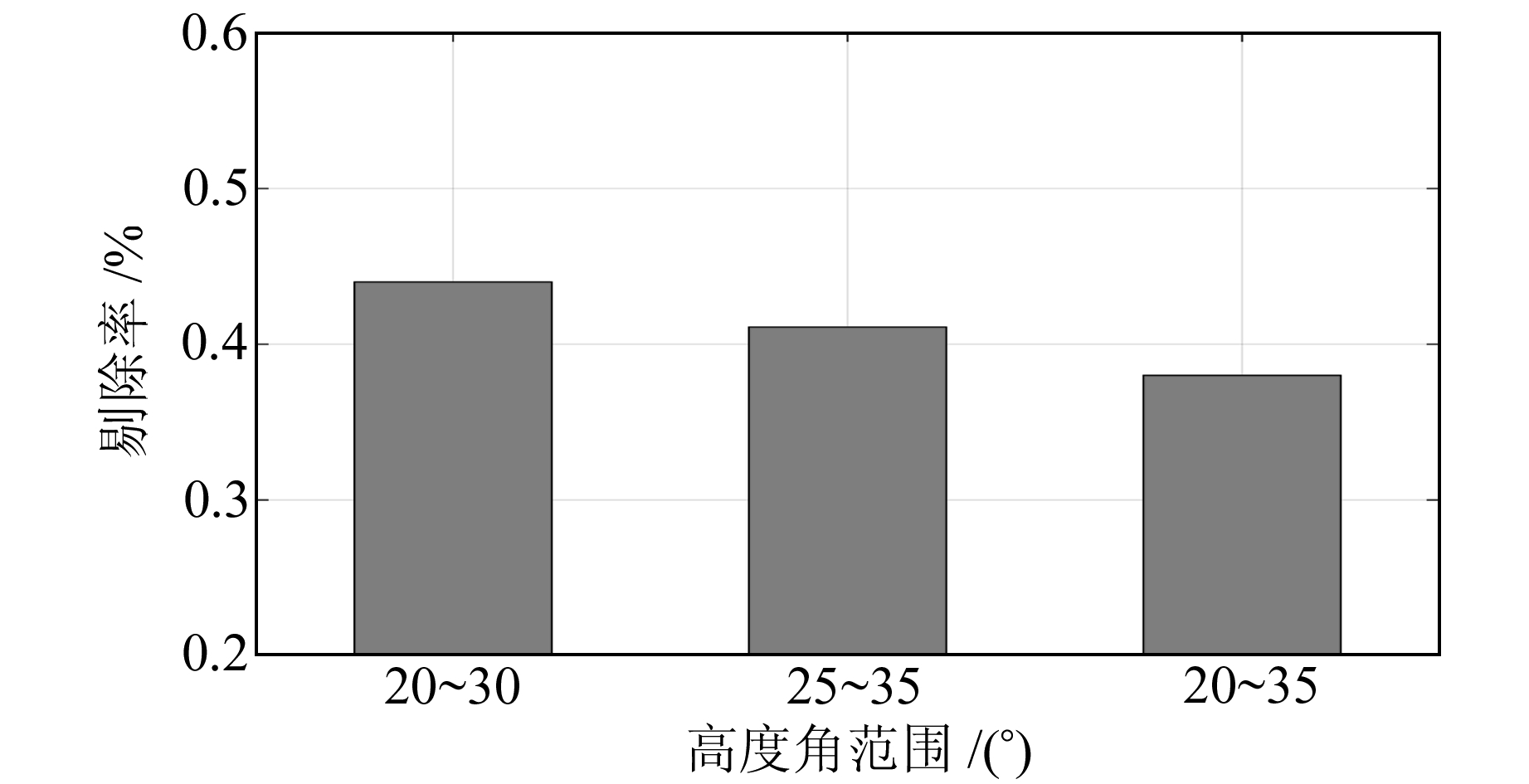
图 8统计了2017年年积日174~249期间卫星高度角在20°~30°、25°~35°、20°~35°范围内SNR反演结果的剔除率均值,其中在20°~35°范围内反演结果具有较低的粗差剔除率,可以保证SNR数据用于水位反演。
|
图 8 不同高度角范围的SNR反演结果剔除率 Fig. 8 SNR inversion results rejection rate for different altitude angle ranges |
用于频谱分析的高度角(20°~35°)的dSNR序列分别为20 min、30 min、45 min、60 min不同弧段长度,通过图 9可以发现,弧段长度与最终的反射距离值有一定的关系,但影响不是很显著。造成各个弧段长度的反演结果精度差别不大的原因是弧段长度较长在本质上只增加了采样率,而利用SNR数据反演水位主要依靠SNR的显著变化和dSNR序列的函数特征,只要SNR变形显著,卫星弧段的长度对于SNR反演精度的影响并不明显。

|
图 9 不同弧段长度的SNR频谱分析 Fig. 9 SNR spectrum analysis of different arc length |
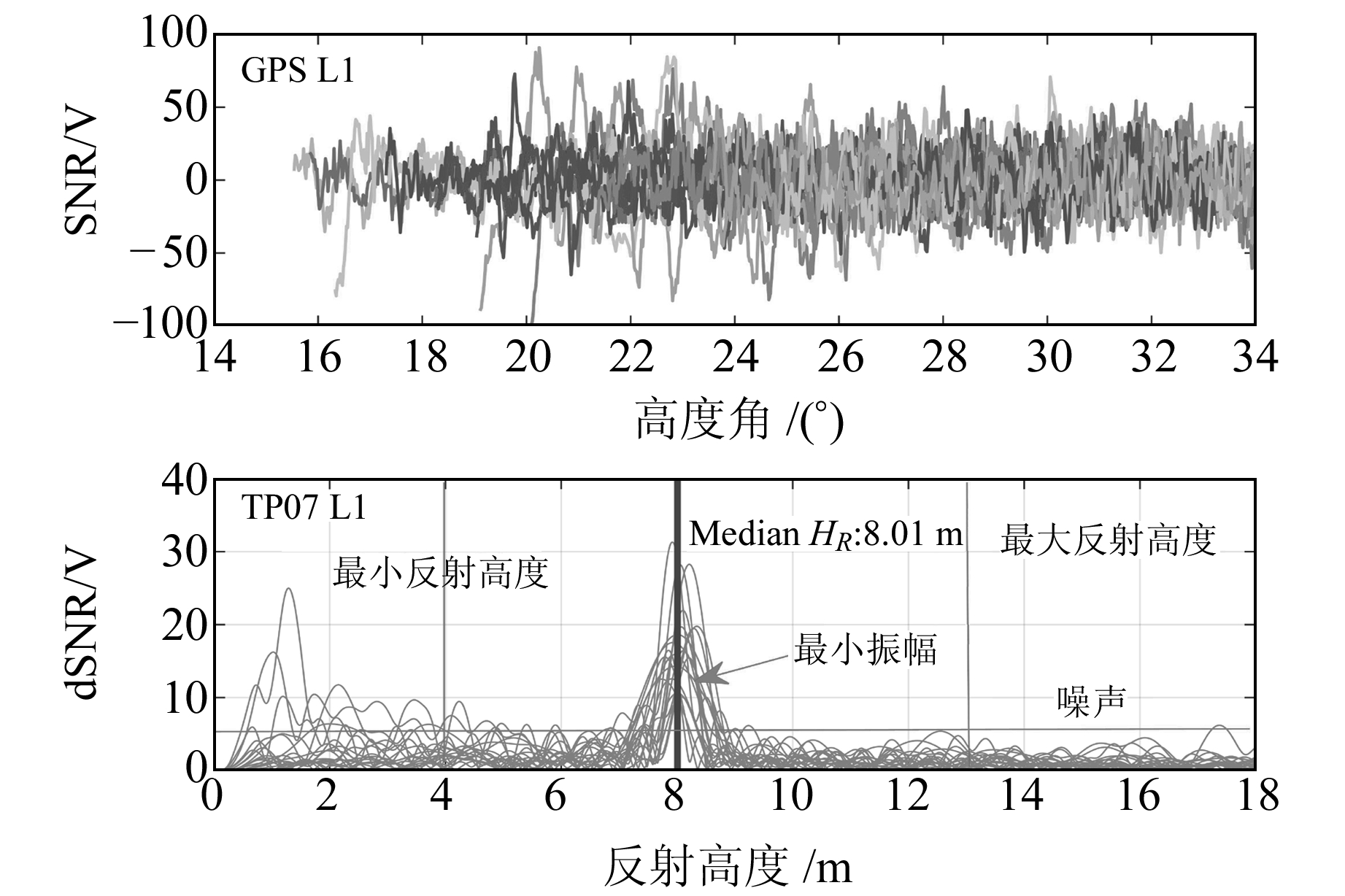
综上所述,考虑大坝实际环境,确定先验最小(大)反射距离minHR(maxHR)、最小振幅minAMP等约束条件,进一步提高反演成功率。为避免水面外反射面的影响,结合实际测量的水位数据,minHR与maxHR分别设置为4 m和13 m。图 10除了大波峰存在的区域,剩余分布在0~5 V范围内的信号当作背景噪声来处理,针对不同星座和不同频率制定最小振幅先验值minAMP,有助于主频信号的确立,通过这些措施进一步增强水位反演结果的可靠性。
|
图 10 模型约束条件 Fig. 10 Model constraint |
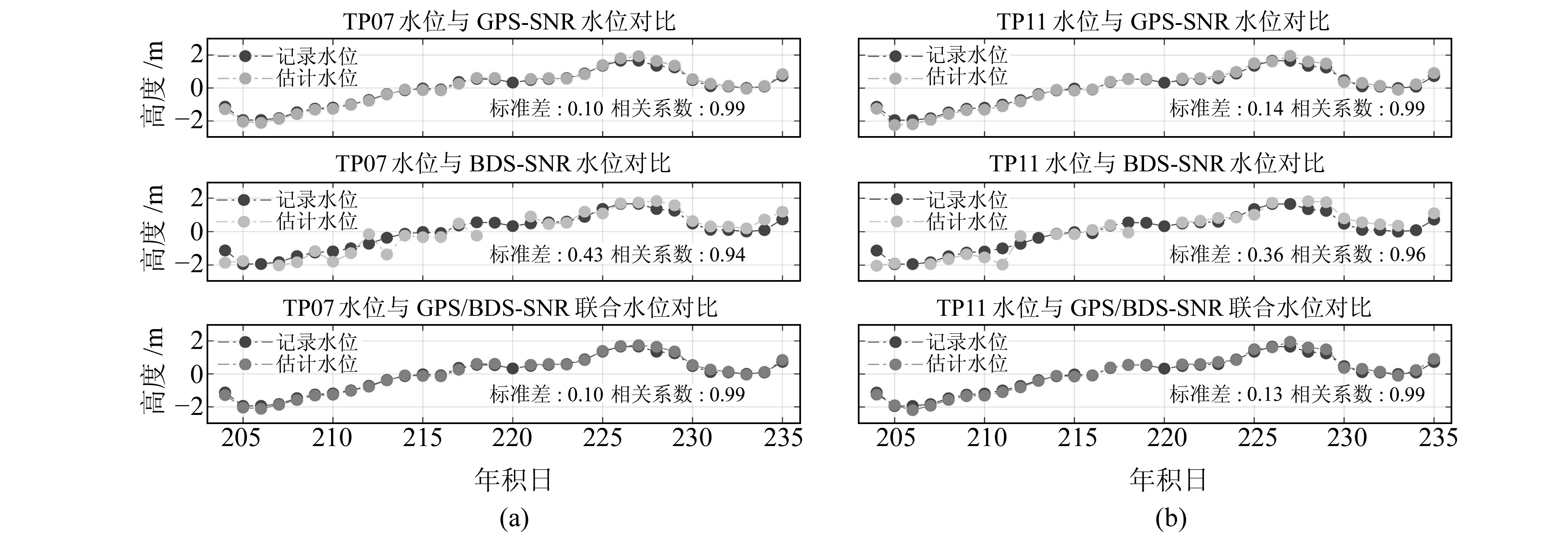
由于实测的水位数据是每天记录1次,水位存在波动,而各个卫星SNR数据反演的结果分布在每天各个时段,如果卫星的观测弧段距离实测记录时间较远,将产生较大偏差。本文的反演结果将采用水位实测记录时间附近的多个卫星SNR数据作为数据来源,选取这些数据的中位数作为当天的估测结果。图 11为TP07测站和TP11测站GPS、BDS及GPS/BDS联合的SNR水位反演结果与实测水位结果的对比,表 2统计了TP07测站和TP11测站水位变化反演结果与实测水位数据的相关系数、中误差、平均偏差、最大偏差和水位变化范围,可以发现,反演结果与实测结果表现出良好的一致性。由表 2可知,GPS和BDS的SNR水位反演结果与实测结果的相关系数均在0.9以上,GPS的反演精度可达0.1 m,而BDS的反演精度为0.35~0.45 m,GPS的反演精度要优于BDS。GPS/BDS联合估计利用的是GPS和BDS双系统的SNR估计值,并选取水位实测记录时间附近的众多SNR估计值的中位数作为最终的结果。
|
图 11 测站年积日204~235的GPS与BDS反演水位和实测水位对比 Fig. 11 Comparison between the GPS/BDS constellation measured water level and estimated water level for doy 204 to 235 |
|
|
表 2 GPS/BDS反演精度对比 Tab. 2 GPS/BDS retrieval accuracy comparison |
从图 11可以看出,尽管已经选取了水位实测记录时间附近的卫星SNR数据作为数据来源,反演高度的中位数作为最终的反演结果,依然与水位实测时间点间隔了较长时间,导致SNR的反演水位与实测记录存在差距,特别是BDS。现阶段BDS可利用的IGSO和MEO卫星较少,很难在实测记录时间附近观测到合适的卫星,导致产生更大的偏差,随着今后BDS卫星的增加将会弥补该缺陷;对于GPS/BDS联合水位估计,GPS依然作为主要的数据贡献源,BDS在某些天改善了GPS的估计结果,增加了系统的可靠性,联合估计结果相比单GPS,精度略有改善。
5 结语本文分析了大坝所处环境下信号频率、高度角范围、弧段长度等影响因素,并根据实际环境建立相应的约束条件,实现了利用GNSS-MR技术反演大坝水位的变化,得出以下结论:
1) 采用GPS L1频率和BDS B1频率将最大地保证卫星利用率和反演成功率;由于大坝附近环境的遮挡及最低高度角的限制,可利用的高度角范围为20°~35°,此范围的SNR数据反演结果具有较低的粗差剔除率和较高的反演精度;卫星高度角较大时,多路径效应微弱,使得反演结果较差。另外,弧段长度对反演结果的精度影响不大。
2) GPS和BDS的SNR水位反演结果与实测记录表现出良好的一致性,相关系数可达0.9以上,GPS的水位反演精度为0.1~0.15 m,BDS的水位反演精度为0.35~0.45 m,GPS/BDS联合反演精度为0.1~0.13 m。
3) GPS和BDS的SNR数据可以用于大坝水位变化的监测,验证了GNSS-MR技术应用于大坝水位变化监测的适用性和有效性。由于现阶段BDS与GPS的可见卫星数量和空间分布存在较大差距,其中BDS的GEO卫星由于高度角变化有限,无法应用于水位反演,因此GPS的水位反演精度高于BDS,GPS/BDS联合反演的精度优于单系统的反演精度。
| [1] |
马海龙. GNSS水位反演方法及其在大坝变形分析中的应用研究[D].武汉: 武汉大学, 2017 (Ma Hailong. Research on GNSS Retrieval of Water Level and Its Application for Dam Deformation Analysis[D]. Wuhan: Wuhan University, 2017) http://cdmd.cnki.com.cn/Article/CDMD-10486-1017179508.htm
(  0) 0) |
| [2] |
金双根, 张勤耘, 钱晓东. 全球导航卫星系统反射测量(GNSS+R)最新进展与应用前景[J]. 测绘学报, 2017, 46(10): 1389-1398 (Jin Shuanggen, Zhang Qinyun, Qian Xiaodong. New Progress and Application Prospects of Global Navigation Satellite System Reflectometry (GNSS+R)[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1389-1398 DOI:10.11947/j.AGCS.2017.20170282)
(  0) 0) |
| [3] |
Bilich A, Larson K M, Axelrad P. Observations of Signal-to-Noise Ratios (SNR) at Geodetic GPS Site CASA:Implications for Phase Multipath[J]. Proceedings of the Centre for European Geodynamics and Seismology, 2004, 23: 77-83
(  0) 0) |
| [4] |
Larson K M, Small E E, Gutmann E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations:Initial Results[J]. GPS Solutions, 2008, 12(3): 173-177 DOI:10.1007/s10291-007-0076-6
(  0) 0) |
| [5] |
Larson K M, Gutmann E D, Zavorotny V U, et al. Can We Measure Snow Depth with GPS Receivers?[J]. Geophysical Research Letters, 2009, 36(17)
(  0) 0) |
| [6] |
Larson K M, Löfgren J S, Haas R. Coastal Sea Level Measurements Using a Single Geodetic GPS Receiver[J]. Advances in Space Research, 2013, 51(8): 1301-1310 DOI:10.1016/j.asr.2012.04.017
(  0) 0) |
| [7] |
Wan W, Larson K M, Small E E, et al. Using Geodetic GPS Receivers to Measure Vegetation Water Content[J]. GPS Solutions, 2015, 19(2): 237-248 DOI:10.1007/s10291-014-0383-7
(  0) 0) |
| [8] |
Ozeki M, Heki K. GPS Snow Depth Meter with Geometry-Free Linear Combinations of Carrier Phases[J]. Journal of Geodesy, 2012, 86(3): 209-219 DOI:10.1007/s00190-011-0511-x
(  0) 0) |
| [9] |
Yu K G, Ban W, Zhang X H, et al. Snow Depth Estimation Based on Multipath Phase Combination of GPS Triple-Frequency Signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 5100-5109 DOI:10.1109/TGRS.2015.2417214
(  0) 0) |
| [10] |
Chew C, Small E E, Larson K M. An Algorithm for Soil Moisture Estimation Using GPS-Interferometric Reflectometry for Bare and Vegetated Soil[J]. GPS solutions, 2016, 20(3): 525-37 DOI:10.1007/s10291-015-0462-4
(  0) 0) |
| [11] |
张双成, 戴凯阳, 南阳, 等. GNSS-MR技术用于雪深探测的初步研究[J]. 武汉大学学报:信息科学版, 2018, 43(2): 234-240 (Zhang Shuangcheng, Dai Kaiyang, Nan Yang, et al. Preliminary Research on GNSS-MR for Snow Depth[J]. Geomatics and Information Science of Wuhan University, 2018, 43(2): 234-240)
(  0) 0) |
| [12] |
Wang X L, Zhang Q, Zhang S G. Water Levels Measured with SNR Using Wavelet Decomposition and Lomb-Scargle Periodogram[J]. GPS Solutions, 2018, 22(1)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


