2. 上海市空间导航与定位技术重点实验室, 上海市南丹路80号, 200030;
3. 西南交通大学地球科学与环境工程学院, 成都市犀安路999号, 611756
鉴于对流层延迟在精密定位等应用中的重要性,国内外学者对其进行了精细建模研究。这些模型大致分为两类: 1)基于理想气体状态方程和大气物理方程的模型,如Hopfield[1]、Saastamoinen[2]、Black[3]等模型,这些模型具有实测气象数据时改正精度可以达到cm级。2)区域性、全球性对流层经验模型,如UNB系列[4-5]、GPT2[6]、EGNOS[7]、GZTD[8]、GPT2w[9]等模型,这些模型仅需要测站位置和年积日就可以实时计算测站对流层延迟改正。国内外学者采用国际GNSS服务的天顶对流层延迟(ZTD)产品、全球大地观测系统(GGOS)ZTD格网产品或GAMIT解算的ZTD产品验证ZTD经验模型在中国区域的精度[10-13],但这些研究存在研究区域较小、选用测站和数据较少或作为参考的数据源精度有限等问题,且没有采用实测气象数据对模型精度与时空特性进行深入研究。基于此,本文采用全球无线电探空资料数据集(IGRA)提供的2017年81个无线电探空站的探空资料,对Saastamoinen、GZTD、UNB3m和GPT2w模型在中国区域的精度和适用性进行综合评估与分析,为对流层延迟模型在中国区域的应用提供参考。
1 模型类型与输入参数表 1为4种对流层延迟模型的类型和输入参数,由表可知,Saastamoinen模型需要测站位置和实测气象数据来计算ZTD,对于缺少气象观测仪器的GNSS测站,该模型的应用受到限制;而其他3种模型仅需输入年积日和测站位置,无需借助测站气象数据就可获取测站的ZTD。因此,这3种经验模型不仅能提供较精确的对流层延迟,也能服务于实时或近实时的应用,如地基GNSS水汽的获取。
|
|
表 1 4种对流层延迟模型的类型与输入参数 Tab. 1 Types and input parameters of the four tropospheric delay models |
本文以IGRA提供的2017年81个探空站的探空资料对4种对流层延迟模型在中国区域的精度进行评估,分析模型随测站位置、季节的变化规律。无线电探空资料提供了标准等压面层的位势高度、绝对温度、相对湿度、风速和风向等信息,其时间分辨率为12 h(UT 00:00, 12:00)[14]。实验选取的无线电探空站分布见图 1。
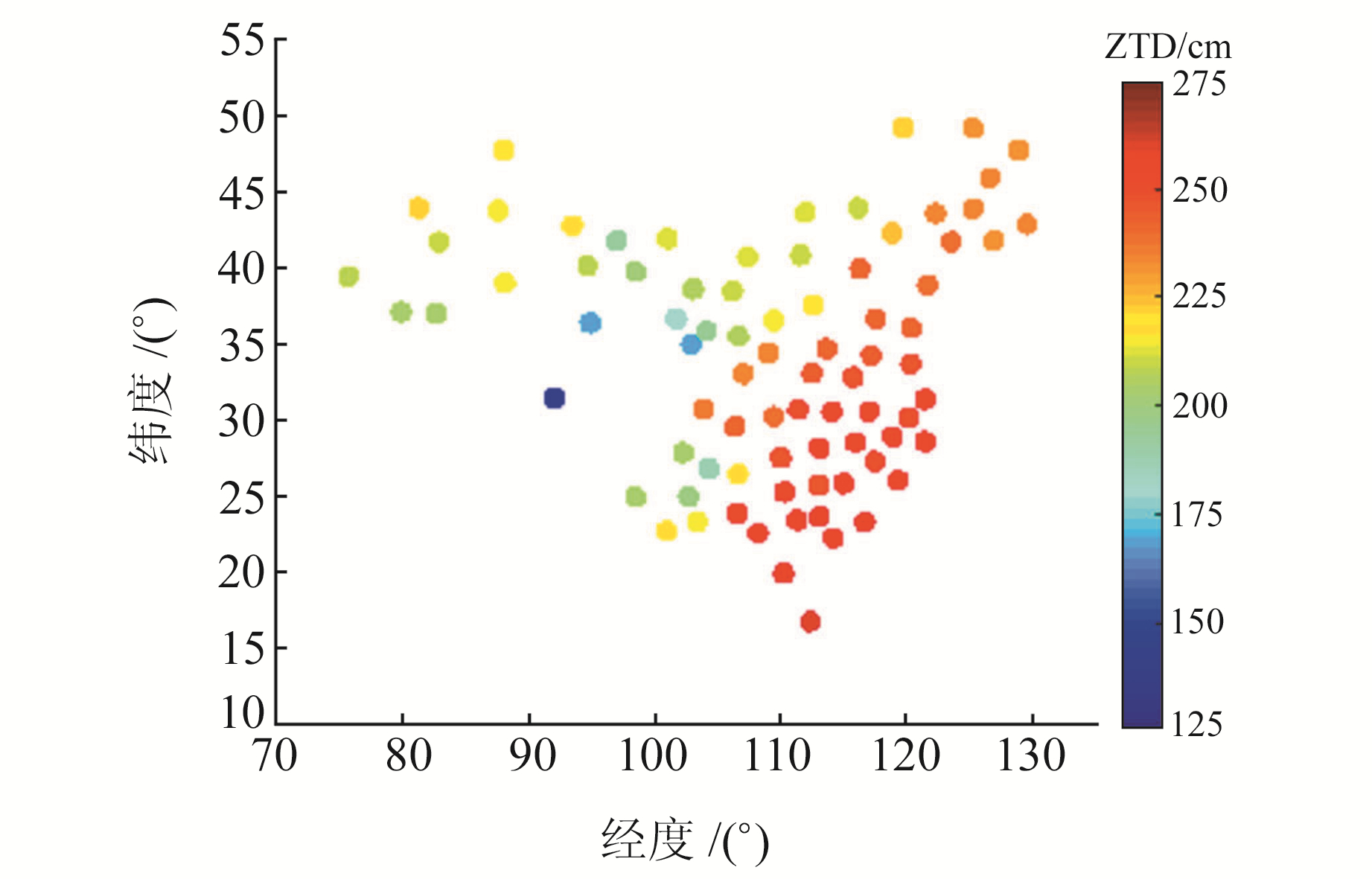
|
图 1 选取的中国区域无线电探空站的分布 Fig. 1 Distribution of selected radiosonde stations in China |
天顶对流层延迟通常以ZHD、ZWD和投影函数的乘积并附加水平梯度来表示[15],而在数值上,ZTD为中性大气折射率的积分:
| $ \mathrm{ZTD}=10^{-6} \int_{0}^{60} N \mathrm{d} s \approx 10^{-6} \sum\limits_{k=1}^{n} N_{k} \Delta h_{k} $ | (1) |
式中,Nk为第k层的大气折射率,Δhk为第k层大气的高差。
大气折射率可以表示为各大气层的气压温度和水汽压的函数[16],具体公式为:
| $ N=N_{\mathrm{dry}}+N_{\mathrm{wet}}=k_{1} \frac{P_{d}}{T}+\left(k_{2} \frac{e}{T}+k_{3} \frac{e}{T^{2}}\right) $ | (2) |
式中,k1、k2和k3均为大气折射系数,这里采用Rüeger[17]提供的经验值。
探空的顶层高度可达10~30 km,超过该高度时水汽对ZWD的贡献很小,因此本文确定各探空站的ZTDref为两个部分的叠加:1)采用探空资料基于式(1)计算探空区间的ZTD0;2)利用Saastamoinen模型结合探空顶层高度的气压计算顶层高度以上的ZHDtop。为确保基于探空资料积分获取ZTD的精度和可靠性,对探空资料等压面层数少于15层及数据缺失率超过25%的部分予以舍弃,GZTD、UNB3m、GPT2w经验模型可采用测站位置直接计算各测站的ZTD模型值,Saastamoinen模型利用探空站最底层实测气象数据计算ZTD。本文以探空资料离散积分确定的ZTDref为参考值,与4种对流层延迟模型的ZTD值求差,并统计各模型在81个探空站的ZTD的MB和RMSE,从而评估和分析模型在中国区域的精度和适用性。
MB和RMSE的具体计算公式为:
| $ \mathrm{MB}=\frac{1}{n} \sum\limits_{k=1}^{n}\left( \mathrm{ZTD}_{\mathrm{mod}, k}-\mathrm{ZTD}_{\mathrm{ref}, k}\right) $ | (3) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{k=0}^{n}\left( \mathrm{ZTD}_{\mathrm{mod}, k}- \mathrm{ZTD}_{\mathrm{ref.}, k}\right)^{2}} $ | (4) |
式中,ZTDmod和ZTDref分别为ZTD模型值和基于气象资料积分的ZTD参考值,n为有效观测数。
3 模型精度对比分析为评估各对流层延迟模型在中国区域的精度和适用性,选取2017年81个无线电探空站的探空资料,基于离散积分确定各测站的ZTD参考值,并计算4种模型的ZTD模型值,统计和分析各模型在中国区域的精度、差异性及其随测站位置、季节的变化特性。
3.1 模型总体精度分析表 2为2017年4种模型在中国区域的精度统计,图 2为ZTD的模型值与探空资料离散积分的参考值,其中,Saas、GZTD、UNB3m和GPT2w ZTD分别代表Saastamoinen、GZTD、UNB3m和GPT2w的ZTD模型值。由表 2和图 2可知,ZTD的模型值总体小于参考值,且各模型的MB均为负值。总体来看,考虑到在中国区域湿度梯度的GPT2w模型要优于另外3种模型,该模型的ZTD模型值与参考值具有很好的一致性,MB和RMSE分别为-0.82 cm和4.45 cm;基于实测气象参数的Saastamoinen模型虽总体精度较高(RMSE为4.46 cm),但模型的MB(系统误差)较大,这是由于对流层湿延迟部分改正精度有限;GZTD模型精度次之,MB和RMSE分别为-1.0 cm、4.93 cm;UNB3m模型的MB较小,但总体精度达到5.76 cm,说明UNB3m模型在部分地区存在较大的正负偏差。
|
|
表 2 4种对流层延迟模型的总体精度 Tab. 2 Overall precision of four tropospheric delay models with respect to the integral of meteorology profiles from radiosonde |
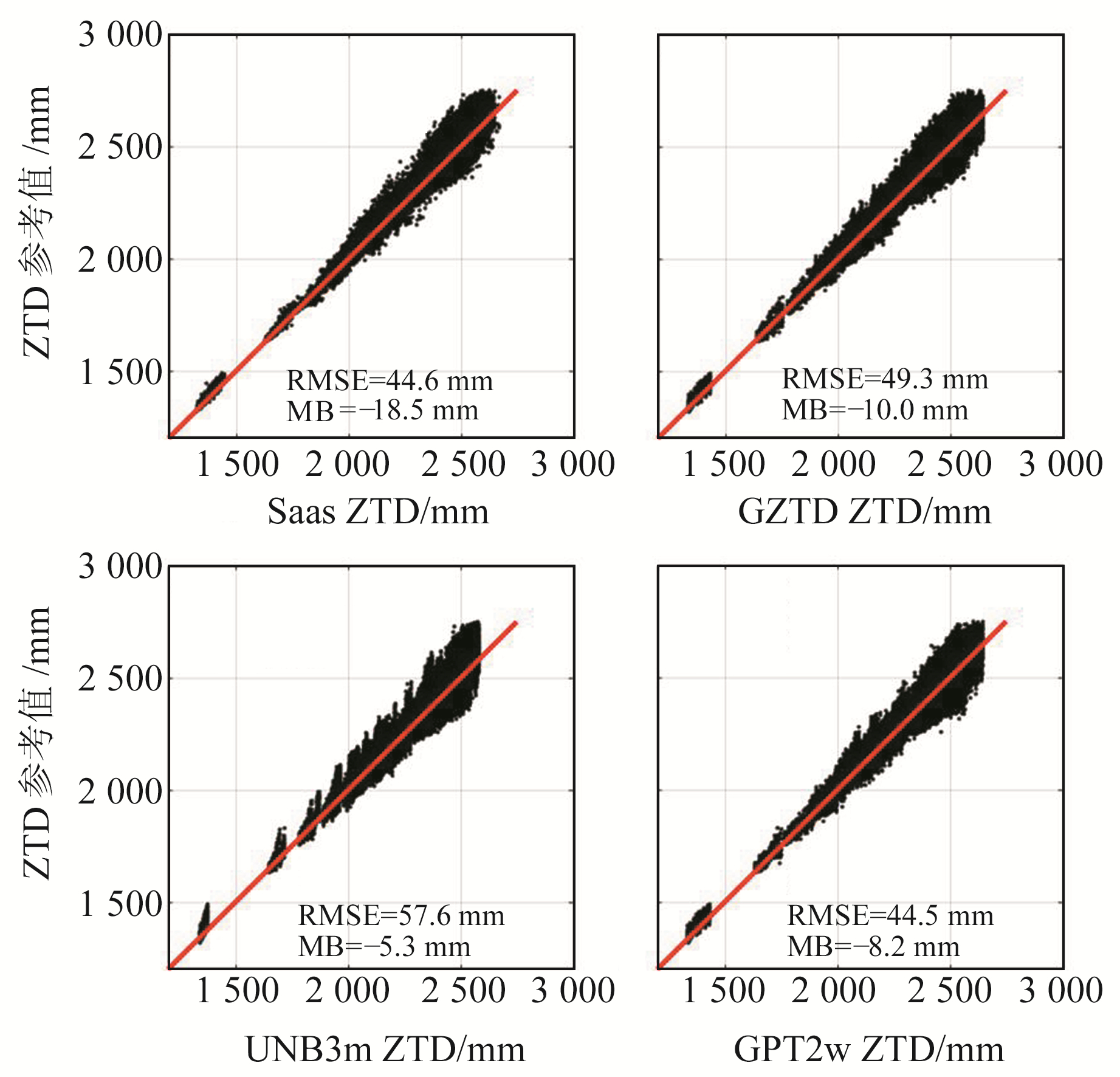
|
图 2 各模型ZTD和气象数据离散积分ZTD Fig. 2 ZTD calculated by the tropospheric delay models and the discrete integral values from meteorology profiles |
图 3~5分别为4种模型的MB、RMSE和相对误差的二维分布,表 3为81个探空站4种经验模型的精度。
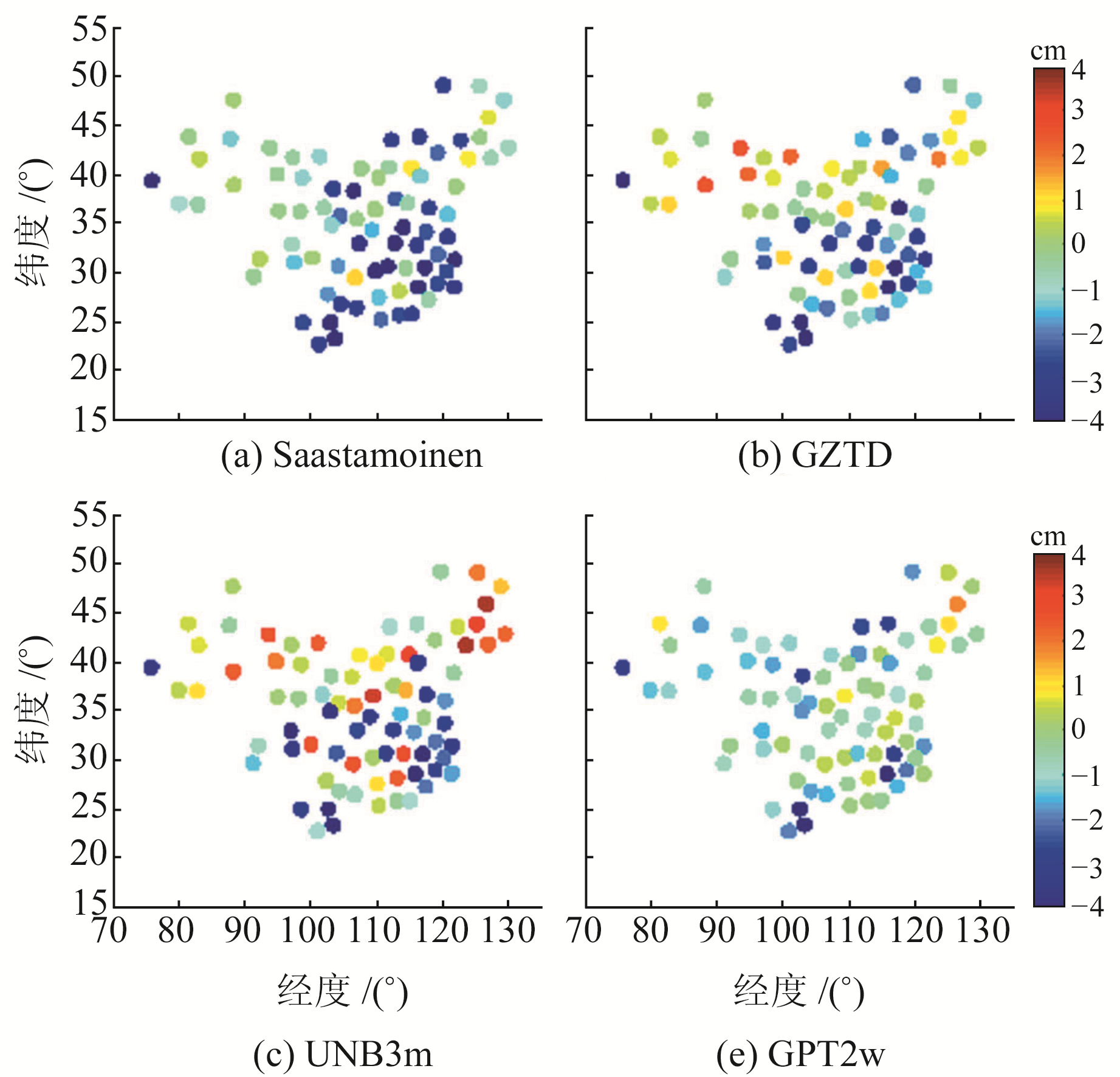
|
图 3 在中国区域4种对流层延迟模型ZTD的MB Fig. 3 Mean bias in ZTD estimates of the four tropospheric delay models over China region |
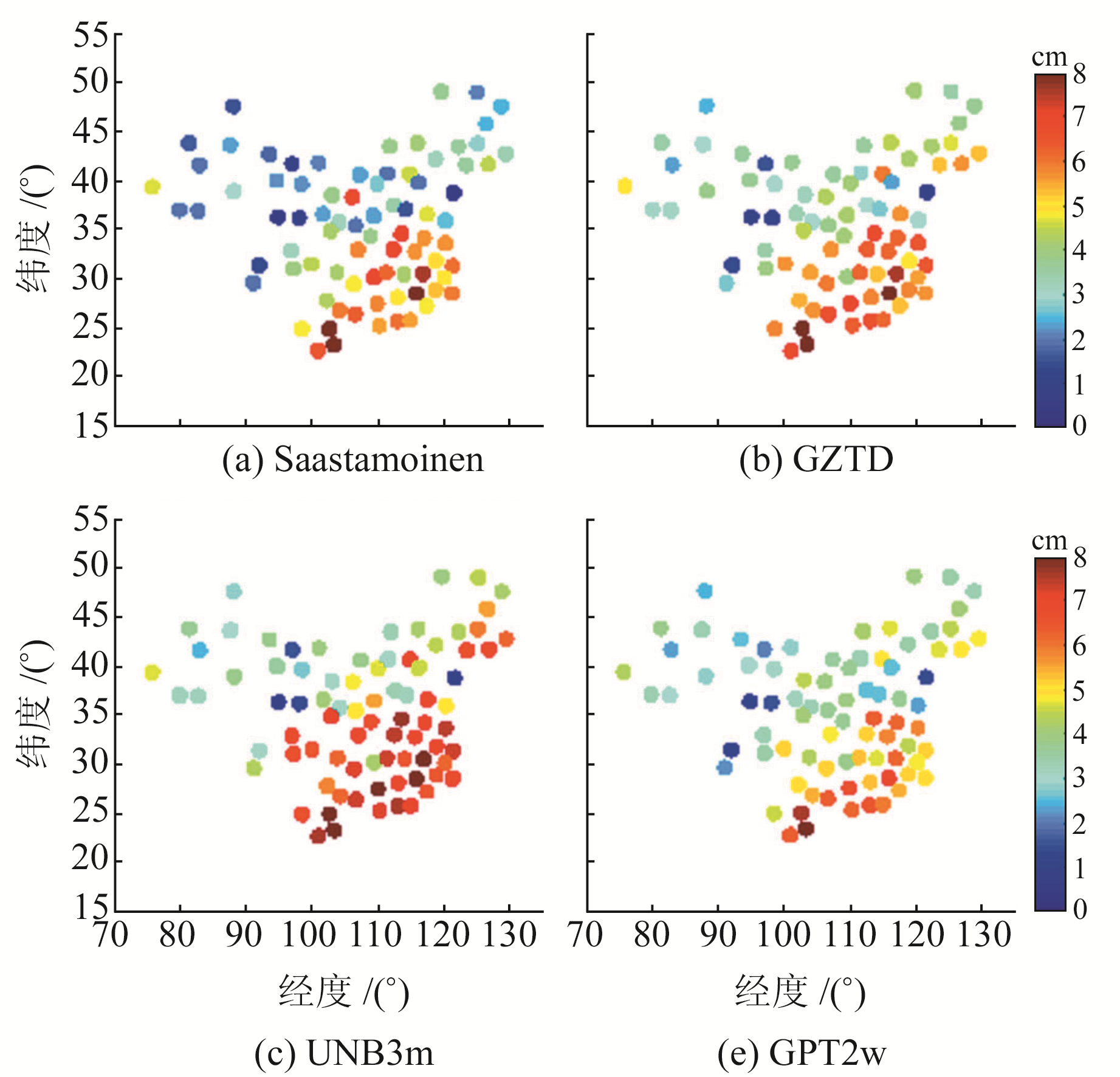
|
图 4 在中国区域4种对流层延迟模型ZTD的RMSE Fig. 4 RMSE of ZTD estimates for the four tropospheric delay models in China region |
|
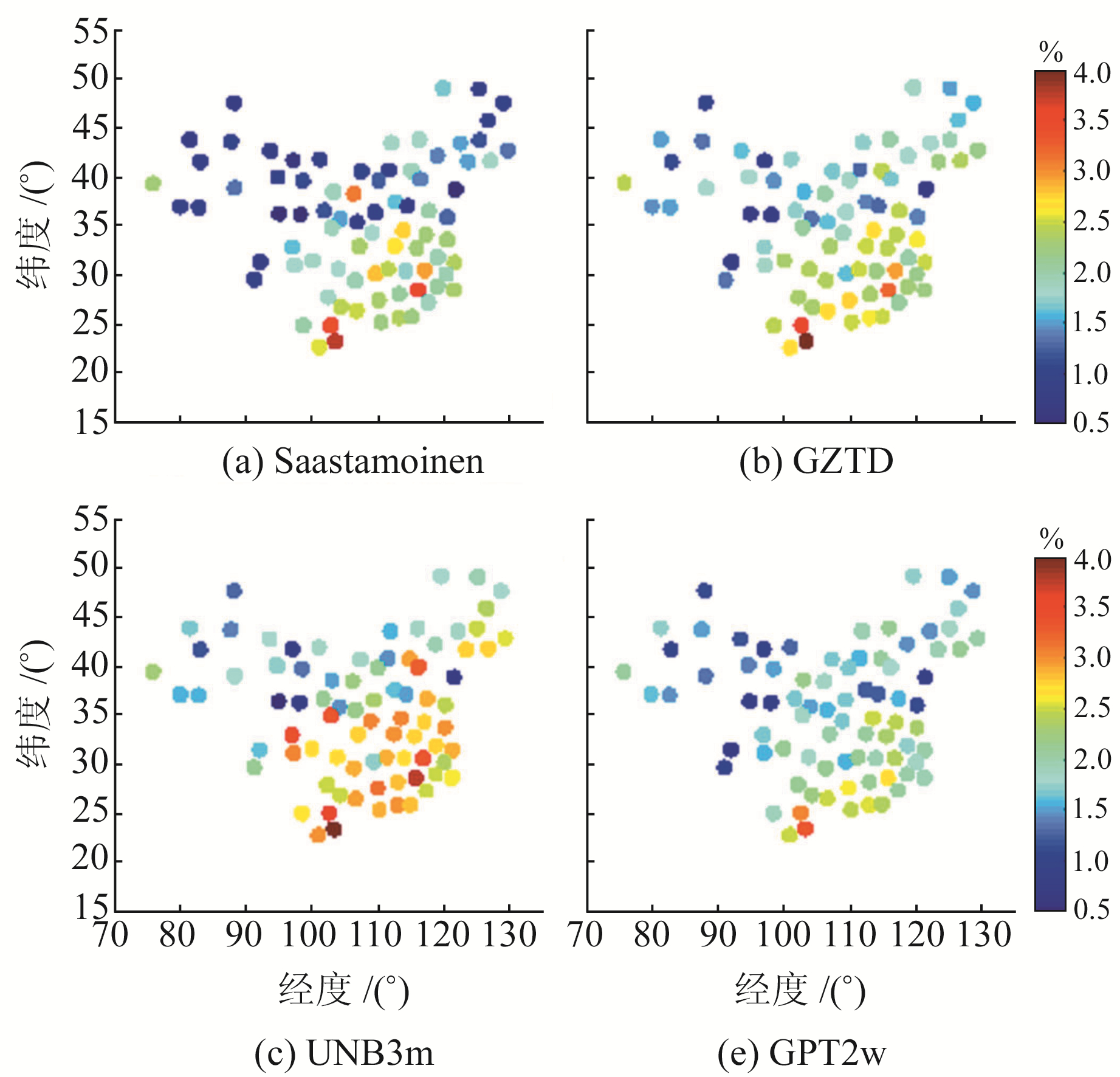
图 5 中国区域4种对流层延迟模型ZTD的相对误差 Fig. 5 Relative error of ZTD estimates for the four tropospheric delay models in china region |
|
|
表 3 各探空站4种对流层延迟模型的精度统计 Tab. 3 Statistics of the precision for four tropospheric delay models at all radiosonde station |
由表 3和图 1、3、5可知,在中国区域4种模型的RMSE和相对误差存在较一致的地域分布特征,表现为在中国西北地区模型的RMSE(< 4 cm)和相对误差(< 2%)较小,而东南沿海地区RMSE(5~8 cm)和相对误差(2.5%~3.5%)较大。这是因为受季风影响的东南沿海地区水汽充沛且变化剧烈,导致对流层湿延迟难以精确估计建模。GPT2w模型的MB较小(均值为-0.8 cm)且分布均匀,各测站MB基本为-2~2 cm,极少数存在较大量级的偏差(-6.0 cm),其RMSE在1.3~7.9 cm之间,均值为4.1 cm;Saastamoinen模型的MB在大部分测站为负值,在南部沿海地区偏差达到-7.6 cm,其RMSE维持在0.6~9.0 cm,均值优于4.0 cm;基于球谐函数的GZTD模型需要对ZTD年均值、季节变化振幅等进行球谐系数展开,并采用单个ZTD垂直递减率进行改正,其精度(MB为-1.0 cm, RMSE均值为4.6 cm)低于GPT2w格网模型,RMSE维持在1.1~9.9 cm。4种模型中,UNB3m模型的精度最差,RMSE均值达到5.4 cm,变化幅度为0.9~10.2 cm,且在大部分测站ZTD存在较大正负偏差(-8.6~3.6 cm)。由各探空站的统计结果来看,在中国区域顾及湿度梯度的GPT2w模型的精度优于Saastamoinen、GZTD和UNB3m模型。
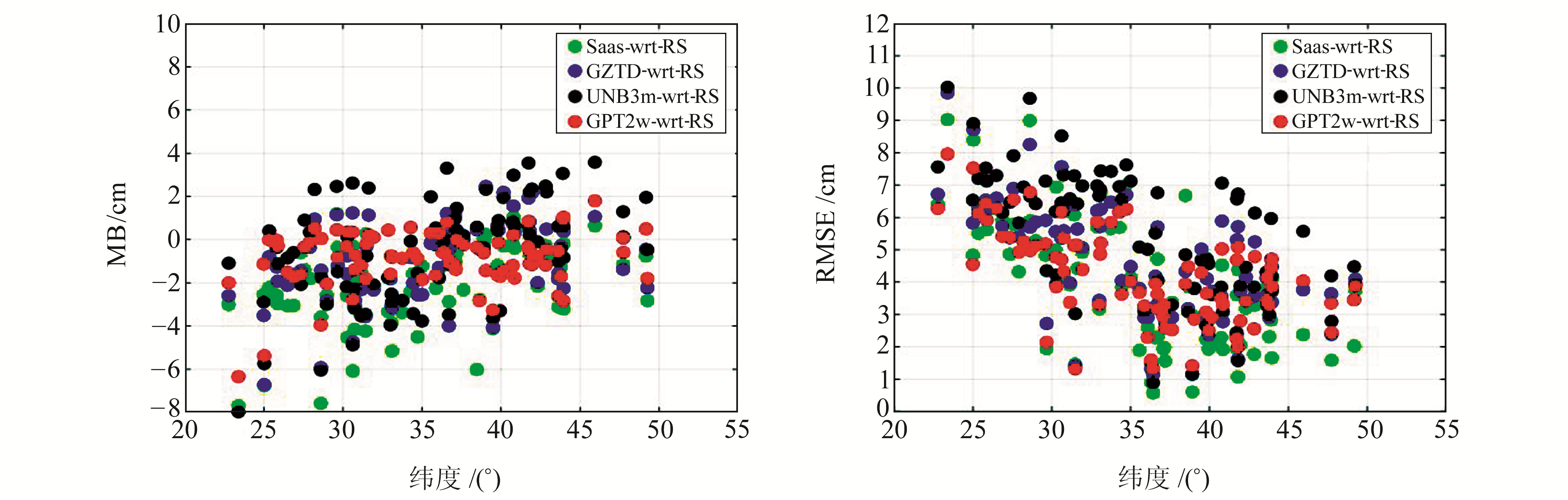
各模型的MB、RMSE与测站位置的关系见图 6~8,图中Saas-wrt-RS、GZTD-wrt-RS、UNB3m-wrt-RS、GPT2w-wrt-RS分别为Saastamoinen、GZTD、UNB3m、GPT2w的ZTD模型值与探空资料ZTD参考值的对比结果。可以看出,4种模型的RMSE随测站纬度的增加呈递减趋势,这种现象与王君刚等[10]的研究成果一致,其原因在于中国区域的低纬度处于东南沿海地区,而该区域水汽充沛且时空变化剧烈,湿延迟分量难以精确估计。各测站GPT2w模型的MB和RMSE分别维持在-2~2 cm和1~6 cm,精度能达到依赖气象数据的Saastamoinen模型的精度。4种对流层延迟模型的MB、RMSE与测站高程和测站经度没有显著相关性。
|
图 6 模型精度随纬度的变化 Fig. 6 Model accuracy varying with latitudes |
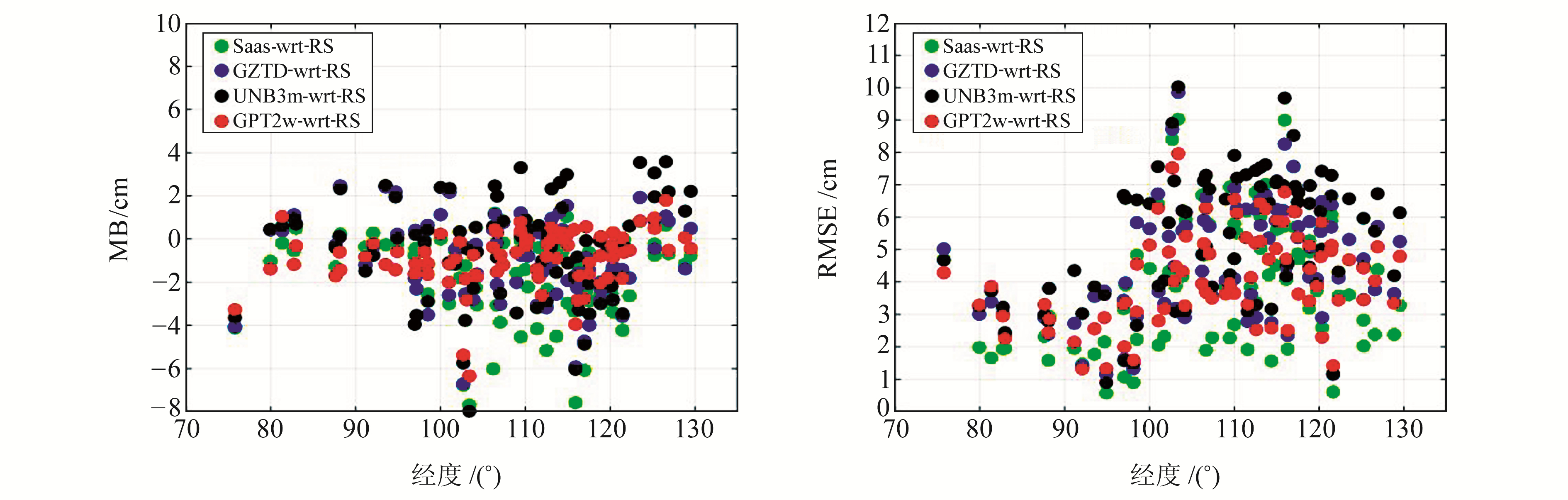
|
图 7 模型精度随经度的变化 Fig. 7 Model accuracy varying with longitudes |
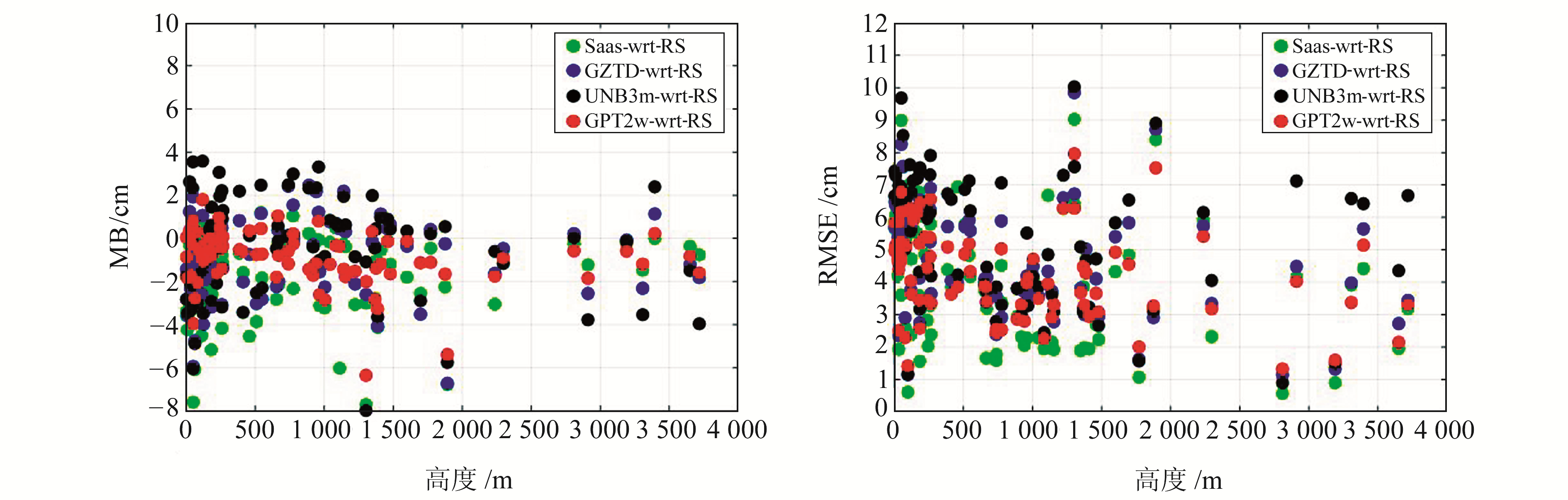
|
图 8 模型精度随高程的变化 Fig. 8 Model accuracy varying with elevations |
图 9为4种模型MB和RMSE的时间序列,由图可知,各模型的MB和RMSE呈明显的季节性变化,这与王君刚等[10]和赵章明等[12]的研究结果一致,模型精度的季节性变化总体表现为夏季较低、冬季较高。Saastamoinen、GZTD、UNB3m和GPT2w模型的RMSE在夏季分别达到峰值6 cm、6 cm、9 cm和7 cm,而在冬季分别达到最低值2 cm、2 cm、2.5 cm和2 cm,模型精度的季节性变化与大气水汽含量及变化剧烈程度相关。中性大气中干大气成分比较稳定,因此干延迟部分建模精度较高;夏季水汽充沛,湿延迟变化剧烈,湿延迟的高频变化难以精确建模估计,造成4种模型精度在夏季较差。2017年Saastamoinen、GPT2w模型的MB在-3~3 cm之间波动,RMSE均在2~6 cm之间波动,年振幅为4 cm;GZTD模型的MB和RMSE分别在-3~3 cm和2~7 cm之间波动, 4种模型中,UNB3m模型的MB和RMSE全年波动较大,分别为-60~40 cm和2.5~10 cm。总体来看,各模型对季节的敏感程度有所差异,GPT2w和Saastamoinen模型的精度在各季节均优于GZTD和UNB3m模型,且UNB3m模型在夏季存在较大偏差,RMSE达到10 cm。

|
图 9 4种对流层延迟模型的MB和RMSE的时间序列 Fig. 9 Time series of MB and RMSE for four tropospheric delay models in contrast with the integral values from meteorology profile |
本文基于IGRA提供的2017年81个无线电探空站的探空资料,对Saastamoinen、GZTD、UNB3m和GPT2w模型在中国区域的精度进行评估与分析,得出以下结论:
1) 顾及湿度梯度的GPT2w模型的精度优于依赖气象数据的Saastamoinen模型、基于球谐函数的GZTD和UNB3m模型。GPT2w模型的平均MB和RMSE分别为-0.8 cm、4.1 cm,各测站的MB和RMSE分别在-2~2 cm和1.3~7.9 cm之间。UNB3m模型在中国区域存在较大偏差,其RMSE最大达到10.2 cm。
2) 对流层延迟模型的精度存在明显季节性变化,且各模型精度对季节的敏感程度有所差异;由于湿延迟高频部分很难精确建模,4种模型的精度在夏季(RMSE为6~9 cm)低于冬季(RMSE为2~2.5 cm)。
3) 4种对流层延迟模型的精度存在一致的地域分布,模型精度对测站纬度具有一致的敏感性,表现为随纬度的升高而降低,但与测站经度和高程没有显著的相关性。
| [1] |
Hopfield H S. Tropospheric Effect on Electromagnetically Measured Range:Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357-367 DOI:10.1029/RS006i003p00357
(  0) 0) |
| [2] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1973, 107(1): 13-34 DOI:10.1007/BF02522083
(  0) 0) |
| [3] |
Black H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research:Solid Earth, 1978, 83(B4): 1825-1828 DOI:10.1029/JB083iB04p01825
(  0) 0) |
| [4] |
Collins J P, Langley R B. Nominal and Extreme Error Performance of the UNB3 Tropospheric Delay Model[R]. Fredericton: Department of Geodesy and Geomatics Engineering, University of New Brunswick, 1999
(  0) 0) |
| [5] |
Leandro R F, Langley R B, Santos M C. UNB3m_Pack:A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2008, 12(1): 65-70 DOI:10.1007/s10291-007-0077-5
(  0) 0) |
| [6] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2:Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073 DOI:10.1002/grl.50288
(  0) 0) |
| [7] |
Penna N, Dodson A, Chen W. Assessment of EGNOS Tropospheric Correction Model[J]. The Journal of Navigation, 2001, 54(1): 37-55 DOI:10.1017/S0373463300001107
(  0) 0) |
| [8] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227)
(  0) 0) |
| [9] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [10] |
王君刚, 陈俊平, 王解先, 等. 对流层经验改正模型在中国区域的精度评估[J]. 武汉大学学报:信息科学版, 2016, 41(12): 1656-1663 (Wang Jungang, Chen Junping, Wang Jiexian, et al. Assessment of Tropospheric Delay Correction Models over China[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1656-1663)
(  0) 0) |
| [11] |
赵静旸, 时爽爽. 对流层天顶延迟模型研究进展及其在中国区域的精度分析[J]. 地球物理学进展, 2018, 33(1): 148-155 (Zhao Jingyang, Shi Shuangshuang. Research Progress of Zenith Tropospheric Delay Model and Its Accuracy Analysis over China[J]. Progress in Geophysics, 2018, 33(1): 148-155)
(  0) 0) |
| [12] |
赵章明, 冯径, 洪亮. 卫星定位中对流层延迟模型对比分析[J]. 测绘通报, 2016(11): 18-21 (Zhao Zhangming, Feng Jing, Hong Liang. Comparison and Analysis of Tropospheric Correction Models in Satellite Positioning[J]. Bulletin of Surveying and Mapping, 2016(11): 18-21)
(  0) 0) |
| [13] |
陈猛, 陈俊平, 胡丛玮. 对流层模型评估及其在GNSS精密单点定位中的应用[J]. 大地测量与地球动力学, 2016, 36(3): 229-234 (Chen Meng, Chen Junping, Hu Congwei. Performance Evaluation of Troposphere Models and Application in GNSS Precise Point Positioning[J]. Journal of Geodesy of Geodynamic, 2016, 36(3): 229-234)
(  0) 0) |
| [14] |
Durre I, Vose R S, Wuertz D B. Overview of the Integrated Global Radiosonde Archive[J]. Journal of Climate, 2006, 19(1): 53-68
(  0) 0) |
| [15] |
Lu C X, Li X X, Nilsson T, et al. Real-Time Retrieval of Precipitable Water Vapor from GPS and Beidou Observations[J]. Journal of Geodesy, 2015, 89(9): 843-856 DOI:10.1007/s00190-015-0818-0
(  0) 0) |
| [16] |
Smith E K, Weintraub S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies[J]. Proceedings of the IRE, 1953, 41(8): 1035-1037 DOI:10.1109/JRPROC.1953.274297
(  0) 0) |
| [17] |
Rüeger J M. Refractive Index Formulae for Radio Waves[C]. FIG XXII International Congress, Washington, 2002
(  0) 0) |
2. Shanghai Key Laboratory of Space Navigation and Positioning Techniques, 80 Nandan Road, Shanghai 200030, China;
3. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, 999 Xi'an Road, Chengdu 611756, China
 2020, Vol. 40
2020, Vol. 40


