2. 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室, 安徽省淮南市泰丰大街168号, 232001;
3. 中国矿业大学环境与测绘学院, 江苏省徐州市大学路1号, 221116;
4. 东南大学仪器科学与工程学院, 南京市四牌楼2号, 210096;
5. 武汉大学测绘学院, 武汉市珞喻路129号, 430079;
6. 淮南矿业(集团)有限责任公司, 安徽省淮南市洞山中路1号, 232001;
7. 中煤新集能源股份有限公司, 安徽省淮南市明惠街1号, 232001
北斗卫星导航系统(BDS)是我国自主建设、独立运行的卫星导航系统,可为全球用户提供全天候、全天时、高精度的定位、导航和授时服务(PNT)[1]。与GPS、GLONASS和GALILEO相比,BDS增加了轨道高度较高、运动角速度较慢的GEO和IGSO卫星[2-3]。周跳探测与修复和整周模糊度解算是实现GNSS高精度定位的关键,GNSS三频观测值可以形成具有波长较短、噪声和电离层影响较小等优良特性的组合观测量,而BDS为全星座发射三频信号,有利于提高BDS周跳探测与修复的精度[4-6]。
本文在前人研究的基础上,利用1个三频载波伪距组合(1, 4, -5)和2个三频无几何相位组合(1, 1, -2)、(1, -2, 1)联合的方法进行周跳探测,结合最小2-范数实现周跳的确定,并利用实测数据验证该算法的有效性。
1 三频实时周跳探测与修复理论 1.1 三频无几何相位组合周跳探测与修复原理根据多频理论,BDS的组合观测方程可表示为[7]:
| $ \begin{array}{c} {\alpha \lambda_{1} \varphi_{1}(t)+\beta \lambda_{2} \varphi_{2}(t)+\gamma \lambda_{3} \varphi_{3}(t)=} \\ {-\eta I(t)+\varepsilon(t)+\lambda_{(\alpha, \beta, \gamma)} N_{(\alpha, \beta, \gamma)}(t)} \end{array} $ | (1) |
式中,λi为载波波长;φi为载波观测值;Ni为整周模糊度;I为B1频点上的电离层延迟误差;α、β和γ分别为组合系数;
无几何(GF)相位组合满足:
| $ \alpha+\beta+\gamma=0 $ | (2) |
当周跳发生时,将GF相位组合进行历元间求差:
| $ \begin{array}{c} \alpha \lambda_{1} \Delta \varphi_{1}+\beta \lambda_{2} \Delta \varphi_{2}+\gamma \lambda_{3} \Delta \varphi_{3} =-\eta \Delta I+\\ \lambda_{(a, \beta, \gamma)} \Delta N_{(a, \beta, \gamma)}+\Delta \varepsilon=-\eta \Delta I+\Delta \varepsilon+\\ \alpha \lambda_{1} \Delta N_{1}+\beta \lambda_{2} \Delta N_{2}+\gamma \lambda_{3} \Delta N_{3} \end{array} $ | (3) |
式中,Δ为单差因子,ΔNi为周跳值。由式(3)可知,通过历元间差分后的GF相位组合仅受ηΔI和Δε的影响,所以在选择GF相位组合时应尽量选择ηΔI和Δε值较小的组合。在高采样率(一般认为1 Hz或更高)条件下,ΔI的值非常小,当η值也非常小时,ηΔI可忽略不计[8],则历元间差分后的GF相位组合探测周跳的条件为:
| $ \begin{aligned} \left|\alpha \lambda_{1} \Delta \varphi_{1}+\beta \lambda_{2} \Delta \varphi_{2}+\gamma \lambda_{3} \Delta \varphi_{3}\right| &=| \Delta \varepsilon+\alpha \lambda_{1} \Delta N_{1}+\\ \beta \lambda_{2} \Delta N_{2}+\gamma \lambda_{3} \Delta N_{3} | & \geqslant n \sigma_{(a, \beta, \gamma)} \end{aligned} $ | (4) |
式中,
三频载波相位与伪距观测值可表示为[9]:
| $ \left\{\begin{array}{c} {\lambda_{i j k} \varphi_{i j k}=\rho-\lambda_{i j k} N_{i j k}(t)+T(t)-} \\ {\eta_{i j k} I_{1}(t)+\delta_{r}+\lambda_{i j k} \varepsilon_{i j k}(t)} \\ {P_{ab c}=\rho+T(t)+\delta_{r}+\eta_{ab c} I_{1}(t)+\varepsilon_{d b c}(t)} \end{array}\right. $ | (5) |
其中,
| $ \left\{\begin{array}{l} {\eta_{i j k}=\frac{\lambda_{i j k}}{\lambda_{1}}\left(i+j \frac{\lambda_{2}}{\lambda_{1}}+k \frac{\lambda_{3}}{\lambda_{1}}\right)} \\ {\eta_{ab c}=a+b\left(\frac{\lambda_{2}}{\lambda_{1}}\right)^{2}+c\left(\frac{\lambda_{3}}{\lambda_{1}}\right)^{2}} \end{array}\right. $ | (6) |
式(5)中,Pabc为伪距组合观测值,系数需满足a+b+c=1,且均为实数;ηijk、ηabc分别为三频载波相位组合观测值与三频伪距组合观测值的电离层放大系数;εijk、εabc为三频载波相位组合观测值与三频伪距组合观测值的观测噪声。将载波相位与伪距组合观测值相减,消除卫地距等项后可得:
| $ \begin{aligned} N_{i j k, a b c}=&\left[\left(P_{a b c}-\lambda_{i j k} \varphi_{i j k}\right)-\left(\eta_{d b c}+\eta_{i j k}\right) I_{1}(t)-\right.\\ &\left.\left(\varepsilon_{a b c}(t)-\lambda_{i j k} \varepsilon_{i j k}(t)\right)\right] / \lambda_{i j k} \end{aligned} $ | (7) |
将式(7)在相邻历元间求差,可得载波伪距组合在相邻历元间的差值(周跳估值)为:
| $ \left\{\begin{array}{c} {\Delta N_{i j k, a b c}=\left(\Delta P_{a b c}-\Delta \varepsilon_{a b c}\right) / \lambda_{i j k}-} \\ {\left(\Delta \varphi_{i j k}-\Delta \varepsilon_{i j k}\right)-\eta_{i j k, a b c} \Delta I_{1}} \\ {\eta_{i j k, a b c}=\left(\eta_{i j k}+\eta_{ab c}\right) / \lambda_{i j k}} \end{array}\right. $ | (8) |
式中,ηijk, abc为三频载波伪距组合观测值的电离层放大系数,Δφijk、Δεijk分别为相邻历元间三频载波组合观测值及其观测噪声的变化量,ΔPabc、Δεabc分别为相邻历元间三频伪距组合观测值及其观测噪声的变化量,ΔI1为相邻历元间B1频率电离层延迟的变化量。
影响周跳探测与修复的关键因素主要与电离层延迟的放大系数及相邻历元间B1频点电离层延迟的变化量有关,当选取的i、j、k与a、b、c系数使得ηijk, abc足够小或采样频率大于1 Hz时,相邻历元间B1频点电离层延迟的变化量ΔI1可忽略不计,此时电离层延迟的影响将被大大削弱,三频载波伪距组合周跳估值可表示为:
| $ \begin{array}{c} \Delta N_{i j k , abc} =\Delta P_{abc} / \lambda_{i j k}-\Delta \varphi_{i j k}-\\ \left(\Delta \varepsilon_{i j k} / \lambda_{i j k}\right.\left.-\Delta \varepsilon_{i j k}\right) \end{array} $ | (9) |
当选取的系数使得对应的λijk足够大时,对应的三频载波伪距组合探测周跳的条件可表示为:
| $ \left\{\begin{array}{l} {\left|\Delta P_{abc} / \lambda_{i j k}-\Delta \varphi_{i j k}-\left(\Delta \varepsilon_{i j k} / \lambda_{i j k}-\Delta \varepsilon_{i j k}\right)\right| \geqslant} \\ n \sigma(\alpha, \beta, \gamma)\\ \sigma_{\Delta N_{i j k, a b c}}=\sqrt{2}\cdot \\ {\sqrt{\left(i^{2}+j^{2}+k^{2}\right) \sigma_{\varepsilon}^{2}+\left(a^{2}+b^{2}+c^{2}\right)\left(\sigma_{e} / \lambda_{i j k}\right)^{2}}} \end{array}\right. $ | (10) |
式中,σε为原始载波相位观测值的噪声水平,σe为原始伪距观测值的噪声水平。
三频载波伪距组合观测值可以保持ΔNijk, abc的整周特性,因此可利用其近似整数解来代替实数解,若能形成3个线性无关的周跳检验量,便可确定周跳值的大小。由于每个系数组合观测值中都存在不敏感的周跳组合,在周跳探测时只要有1个检验量大于阈值,即可认定该处存在周跳。
2 组合观测值系数的确定本文采用1个三频载波伪距组合观测值和2个三频GF相位组合观测值联合的方法进行周跳探测。式(3)中的GF相位组合系数需满足α+β+γ=0,min(δΔNαβγ),ηαβγ→0,组合系数较小可以减少多路径的影响,组合系数较大会使GF相位组合观测值中的δΔNαβγ减小,但会增加周跳搜索的范围,因此本文在±4范围内搜索最优的GF相位组合系数,部分最优组合对应的相关参数见表 1。
|
|
表 1 部分较优的GF相位组合系数 Tab. 1 Partially superior GF phase combination |
由表 1可知,(1, 0, -1)、(1, -1, 0)组合虽然噪声较小,但由于2个频点比较接近,不敏感的周跳数目较多,只能实现双频的周跳探测;(1, 2, -3)、(1, 3, -4)组合具有较小的电离层延迟放大系数,但噪声较大,在采样频率较低或电离层延迟变化幅度大的情况下具有较大优势;而(1, 1, -2)、(1, -2, 1)组合的电离层延迟放大系数与噪声都较为适中。选取2组不同的GF相位组合同时进行周跳探测可大大减小不敏感周跳的数目,不同GF相位组合检验量在10周与100周内的不敏感周跳数目见表 2。
|
|
表 2 GF相位组合的阈值及不敏感周跳个数 Tab. 2 The threshold of geometry-free phase combination and the number of insensitive cycle-slip |
由表 2可知,所有组合均能探测出10周内的周跳,而对10~100周内的周跳只有1个存在不敏感现象,可利用载波伪距组合法进行探测;同时,由于(2, 1, -3)、(1, 3, -4)、(1, -2, 3)组合具有较大的噪声,(1, -1, 0)、(0, 1, -1)组合频点较近,不敏感周跳较大,只能实现双频的周跳探测,因此本文选取(1, 1, -2)、(1, -2, 1)组合作为第1、第2 GF相位组合周跳检验量。
三频载波伪距组合观测值具有较长的波长、较小的电离层放大系数和较小的噪声,因此首选超宽巷、宽巷组合。同时注意到,当ηijk, abc足够小时,其对周跳检验量的影响可以忽略,故应满足a=b=c的条件;另外由式(5)可知,a+b+c=1,因此取a=b=c=1/3。本文在±10范围内搜索最优的载波伪距组合系数,部分结果见表 3。
|
|
表 3 部分较优的载波伪距组合系数 Tab. 3 Carrier pseudorange combination and its threshold |
由表 3可知,若电离层在历元间的变化量为0.15 m,电离层延迟对(1, 4, -5)、(0, -1, 1)、(1, 3, -4)组合周跳探测的影响也小于0.5周,仍可准确实现周跳的探测;(-1, -5, 6)组合的波长最长,但其对应的其他系数都较(1, 4, -5)组合的大,而(0, -1, 1)、(1, 3, -4)组合虽然对应的系数也较小,但波长明显短于(1, 4, -5)组合的波长,因此本文选取(1, 4, -5)组合作为载波伪距组合第3检验量。
采用1个三频载波伪距组合(1, 4, -5)和2个三频GF相位组合观测值(1, 1, -2)、(1, -2, 1)联合进行周跳探测时,建立联立方程:
| $ \boldsymbol{A X=L} $ | (11) |
式中,
| $ \Delta \xi=\|\boldsymbol{A} \hat{X}-\boldsymbol{L}\|^{2} $ | (12) |
2018-01-23的16时,在安徽理工大学利用海星达H32系列接收机(GPS L1/L2,BDS B1/B2/B3,GLONASS R1/R2)进行实验,采样率设置为1 s,截止高度角设置为15°。数据处理时,取伪距噪声标准误差B1/B2为0.3 m、B3为0.2 m,载波噪声水平均为0.01周。为验证本文算法,选择“干净”的C01和C06卫星进行分析,分别人工加入一般周跳(3个组合均能探测的周跳)、不敏感周跳及连续随机周跳进行周跳探测。
3.1 一般周跳探测与修复在第1 842 s对C01和C06卫星加入一般周跳,探测结果见图 1和2。

|
图 1 C01卫星一般周跳探测 Fig. 1 The normal cycle-slip detection for C01 |

|
图 2 C06卫星一般周跳探测 Fig. 2 The normal cycle-slip detection for C06 |
由图 1(a)和2(a)可知,载波伪距组合(1, 4, -5)的观测噪声要大于GF相位组合(1, 1, -2)和(1, -2, 1),这是因为载波伪距组合(1, 4, -5)引入了观测噪声较大的伪距观测值;图 1(b)和2(b)分别在B1频点上加入1周周跳,而3种组合的检验量均超过了各自的阈值,达到了探测周跳的效果;图 1(c)和2(c)在3个频点上分别加入小周跳(2, 1, 3),3种组合也均能探测出周跳;图 1(d)和2(d)在3个频点上分别加入周跳(9, 100, 17),3种组合的检验量均大大超过了各自的阈值,也均能探测出周跳。结果表明,本文方法可对一般周跳进行很好的探测。
3.2 不敏感周跳探测与修复在第1 842 s对C01和C06卫星分别加入3组(1, 3, 2)、(10, 10, 10)和(75, 58, 61)不敏感周跳,探测结果见图 3和4。

|
图 3 C01卫星不敏感的周跳探测 Fig. 3 The insensitive cycle-slip detection for C01 |
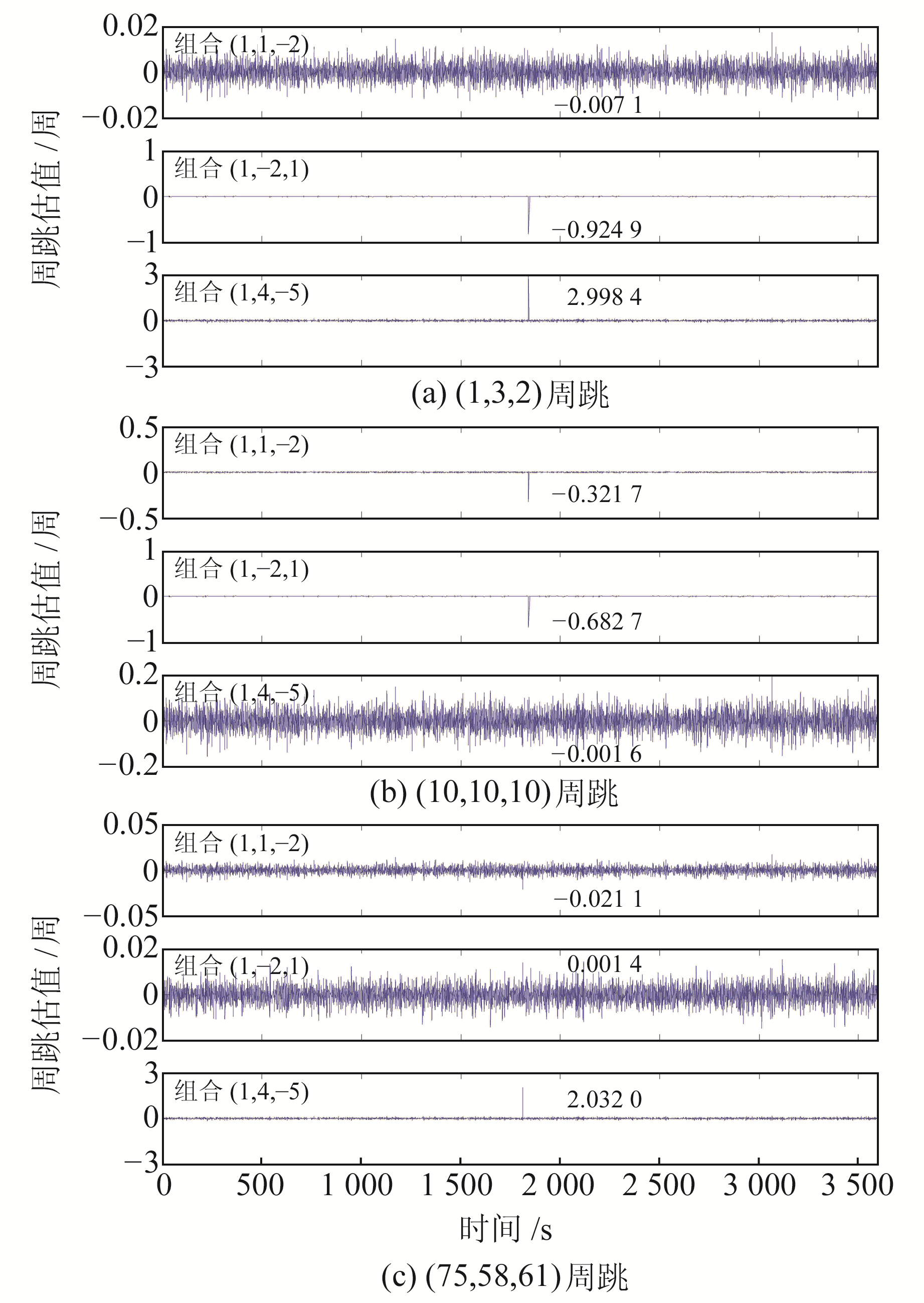
|
图 4 C06卫星不敏感的周跳探测 Fig. 4 The insensitive cycle-slip detection for C06 |
由图 3和4可知,GF相位组合(1, 1, -2)无法探测出周跳(1, 3, 2),而GF相位组合(1, -2, 1)和载波伪距组合(1, 4, -5)可以很好地探测出该周跳;载波伪距组合(1, 4, -5)无法探测出周跳(10, 10, 10),而GF相位组合(1, -2, 1)和(1, -2, 1)可以很好地将其探测出来;周跳(75, 58, 61)利用GF相位组合(1, -2, 1)和(1, -2, 1)探测时不敏感,但其可被载波伪距组合(1, 4, -5)探测到。通过分析可知,有些不敏感周跳可能对部分探测组合不敏感,但3种组合联合后均能很好地探测出周跳,从而大大减少了探测“盲区”。
3.3 随机连续周跳探测与修复为进一步验证本文方法对周跳探测的效果,在C01与C06卫星的第1 842~1 846 s处分别加入随机连续周跳(0, 1, 2)、(1, 0, 0)、(1, 1, 1)、(3, 4, 5)和(10, 30, 1),探测结果见图 5和6,表 4为3种组合对随机连续周跳的探测检验量及修复结果。

|
图 5 C01随机连续周跳探测 Fig. 5 The continuous cycle-slip detection for C01 |

|
图 6 C06随机连续周跳探测 Fig. 6 The continuous cycle-slip detection for C06 |
|
|
表 4 连续随机周跳模拟值及修复值 Tab. 4 The simulation value and repair value of continuous random cycle-slip |
由图 5、6和表 4可知,采用1个三频载波伪距组合(1, 4, -5)和2个三频GF相位组合观测值(1, 1, -2)、(1, -2, 1)联合的方法不仅可探测出5周内的连续小周跳,还可探测出30周的大周跳,并通过最小2-范数搜索出正确的整数周跳值。实验结果进一步表明了本文算法的有效性。
4 结语本文根据GF相位组合有利于小周跳探测的优点,选择2个较优的GF相位组合(1, 1, -2)和(1, -2, 1)并联合载波伪距组合(1, 4, -5),构成3个线性无关的周跳探测组合,对一般周跳(3个组合均能探测的周跳)、不敏感周跳及连续随机周跳进行了周跳探测,实验结果表明,该联合算法可以很好地探测所有周跳。为进一步确定周跳值的大小,采用最小2-范数对整数周跳的搜索策略进行确定,搜索结果与周跳的模拟值一致,表明该联合算法可以很好地修复周跳。本文算法只利用了历元间差分,因此也适用于非差定位的周跳探测与修复。
| [1] |
北斗卫星导航系统介绍.http://www.beidou.gov.cn/xt/xtjs/, 2018 (Introduction of Beidou Satellite Navigation System. http://www.beidou.gov.cn/xt/xtjs/, 2018)
(  0) 0) |
| [2] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [3] |
Li X, Li X X, Liu G G, et al. Spatial-Temporal Characteristic of BDS Phase Delays and PPP Ambiguity Resolution with GEO/IGSO/MEO Satellites[J]. GPS Solutions, 2018, 22(4): 123-127 DOI:10.1007/s10291-018-0790-2
(  0) 0) |
| [4] |
Zhao Q L, Sun B Z, Dai Z Q, et al. Real-Time Detection and Repair of Cycle Slips in Triple-Frequency GNSS Measurements[J]. GPS Solutions, 2015, 19(3): 381-391 DOI:10.1007/s10291-014-0396-2
(  0) 0) |
| [5] |
Huang L Y, Lu Z P, Zhai G J, et al. A New Triple-Frequency Cycle Slip Detecting Algorithm Validated with BDS Data[J]. GPS Solutions, 2016, 20(4): 761-769 DOI:10.1007/s10291-015-0487-8
(  0) 0) |
| [6] |
刘柳, 吕志伟, 于晓东, 等. GNSS三频周跳探测与修复算法[J]. 测绘学报, 2017, 46(4): 453-459 (Liu Liu, Lü Zhiwei, Yu Xiaodong, et al. Real-Time Cycle-Slip Detection and Repair Algorithm of GNSS Triple-Frequency Observations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 453-459)
(  0) 0) |
| [7] |
吕伟才, 高井祥, 王坚, 等. 北斗三频约束的短基线模糊度单历元算法[J]. 中国矿业大学学报, 2015, 44(6): 1090-1096 (Lü Weicai, Gao Jingxiang, Wang Jian, et al. The Single Epoch Algorithm for Short Baseline Ambiguity Based on Beidou Three Frequency Constraint[J]. Journal of China University of Mining and Technology, 2015, 44(6): 1090-1096)
(  0) 0) |
| [8] |
伍岳, 郭金来, 孟央, 等. GPS多频相位组合观测值的定位精度分析[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1082-1085 (Wu Yue, Guo Jinlai, Meng Yang, et al. Analysis of GPS Multi-Frequency Carrier Phase Combinations[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1082-1085)
(  0) 0) |
| [9] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722 (Li Jinlong, Yang Yuanxi, Xu Junyi, et al. Real-Time Cycle-Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Un-Differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722)
(  0) 0) |
| [10] |
Liu W K, Jin X Y, Wu M K, et al. A New Real-Time Cycle Slip Detection and Repair Method Under High Ionospheric Activity for a Triple-Frequency GPS/BDS Receiver[J]. Sensors, 2018, 18(2): 427 DOI:10.3390/s18020427
(  0) 0) |
| [11] |
李星星.GNSS精密单点定位及非差模糊度快速确定方法研究[D].武汉: 武汉大学, 2013 (Li Xingxing. Rapid Ambiguity Resolution in GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm
(  0) 0) |
2. Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, 168 Taifeng Street, Huainan 232001, China;
3. School of Environmental Science and Spatial Informatics, China University of Mining And Technology, 1 Daxue Road, Xuzhou 221116, China;
4. School of Instrument Science and Engineering, Southeast University, 2 Sipailou, Nanjing 210096, China;
5. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
6. Huainan Mining Group Co Ltd, 1 Mid-Dongshan Road, Huainan 232001, China;
7. China Coal Xinji Energy Co Ltd, 1 Minghui Street, Huainan 232001, China
 2020, Vol. 40
2020, Vol. 40

