2. 华东交通大学土木建筑学院, 南昌市双港东大街808号, 330013;
3. 中铁第一勘察设计院集团有限公司轨道交通工程信息化国家重点实验室, 西安市西影路2号, 710043
GNSS坐标时间序列具有非线性、非平稳性等特点,如何对其进行降噪处理是目前研究的热点。EMD方法[1]是一种自适应的时频分析方法,张双成等[2]利用该方法分析GNSS位置时间序列,结果表明,该方法能将线性趋势项、周期项、噪声从原始序列中有效地分离出来,并能准确地提取出周期项;胡爱军等[3]的研究表明,模态分解中存在模态混叠现象。利用集总经验模态分解(ensemble empirical mode decomposition,EEMD)虽然可以在一定程度上抑制模态混叠现象,但IMF分量的个数受所加噪声的影响可能不同,且其计算量较大[4-5]。罗飞雪等[6]考虑到交叉认证方法能自适应平滑信号,将其与EMD滤波去噪方法结合,实现了噪声和信号的有效分离,削弱了多路径的影响,但交叉认证过程比较复杂。梁喆等[7]考虑到分界IMF分量中模态混叠的问题,将EMD方法和互信息熵相结合,提出一种自适应提取信号的算法,虽能提取微震信号,但需要确定抑制高频IMF分量噪声的阈值。贾瑞生等[8]采用独立成分分析(ICA)的盲源分离技术,消除经EMD方法分解得到的IMF分量上的混叠噪声,有效提取出真实的微震信号,但需要构造ICA算法的多维输入向量。肖小兵等[9]将EMD与奇异谱分析方法相结合,提出一种信号去噪方法,但奇异谱分析方法需要选择合适的窗口。以上研究通过时频分析实现了信噪分离,但存在一定的缺陷,只能提取出高频分界IMF分量中含有的细节信息,未考虑多个高频IMF分量中的细节信息[10]。
本文改进的EMD降噪方法重复对每次EMD得到的第2个IMF分量至分界IMF分量进行重构,得到新的序列数据,最后将所得的所有低频IMF分量进行重构,提取出高频噪声中的“真实”信号。
1 EMD降噪理论及其改进 1.1 EMD降噪的基本原理EMD降噪的基本思想是把信号分解为一系列频率由高到低的IMF分量和残差项(趋势项),然后将残差项与邻近的低频IMF分量重构为降噪信号[11]。通过相关系数准则确定分界IMF分量,相关系数第1次取得极小值时所对应的IMF分量即为分界IMF分量。每个IMF分量需要满足以下2个条件:1)在整个序列中,过零点的数目与极值点的数目最多相差1个;2)由局部极大值所构成的上包络线及局部极小值所构成的下包络线的平均值为0。
根据EMD方法的步骤,原始数据序列x(t)可表示为:
| $ x(t)=\sum\limits_{k=1}^{m} \operatorname{IMF}_{k}+r(t) $ | (1) |
式中,m表示分解得到的IMF分量的总个数,k表示IMF分量的顺序。
在实际信号分解中,IMF分量很难严格满足由局部极值组成的上、下包络线的均值为0的条件,给出IMF分量停止筛选的阈值表达式为:
| $ \mathrm{SD}=\sum\limits_{t=0}^{N-1}\left[\frac{\left(c_{k}(t)-c_{k-1}(t)\right)^{2}}{c_{k}^{2}(t)}\right] $ | (2) |
式中,SD表示每个IMF分量停止筛选的阈值,通常情况下取0.2~0.3,ck(t)、ck-1(t)表示筛选过程中相邻的2个数据序列。
EMD方法将分界IMF分量并入噪声部分、分界之后的低频IMF分量及残差项中进行重构,得到降噪信号。降噪后的信号可表示为:
| $ \hat{x}(t)=\sum\limits_{k=K+1}^{m} \operatorname{IMF}_{k}+r(t) $ | (3) |
式中,
利用EMD方法,将原始数据序列x1分解为一系列频率由高到低的本征模态函数分量IMF1m1及一个残差项r1(t);将第2个IMF12分量至分界本征模态函数分量IMF1K1进行重构,获得一个新的原始数据序列x2,再次利用EMD方法对x2进行分解,得到若干频率由高到低的本征模态函数分量IMF2m2及一个残差项r2(t);将此次分界本征模态函数分量IMF1K2到第2个IMF22分量进行重构,再次得到一个新的原始数据序列x3,重复上述操作,能够得到新的数据序列xi,利用EMD方法得到若干IMFimi分量及残差项ri(t)。最终将所有低频IMF分量及残差项进行重构,得到降噪后的数据序列,可表示为:
| $ \begin{array}{c} \hat{x}_{1}=\sum\limits_{m_{1}=K_{1}+1}^{M_{1}} \operatorname{IMF}_{1 m_{1}}+\sum\limits_{m_{2}=K_{2}+1}^{M_{2}} \operatorname{IMF}_{2 m_{2}}+\cdots+\\ \sum\limits_{m_{i}=K_{i}+1}^{M_{i}} \operatorname{IMF}_{i m_{i}}+\sum\limits_{j=1}^{i} r_{j}(t) \end{array} $ | (4) |
式中,Ki表示第i个原始数据序列噪声共存的阶次,Mi表示第i个原始数据序列总的IMF分量的个数,IMFimi表示第i个原始数据序列的第mi个IMF分量,rj(t)表示第j次EMD的残余项。本文只进行3次EMD,即i的值取3。
模拟数据真值已知,采用相关系数(P)、均方根误差(RMSE)、信噪比(SNR)等传统评价指标来衡量去噪的效果,P值越接近1,RMSE值越小,SNR值越大,去噪效果越好。由于实测数据含有噪声,可能导致3种评价值所评价的降噪效果不一致。针对此问题,引入一种更加可靠的复合评价指标T进行降噪效果的评价[12]。复合评价指标T考虑了呈负相关的均方根误差与平滑度指标,T值越小,降噪效果越好,具体公式见参考文献[12]。
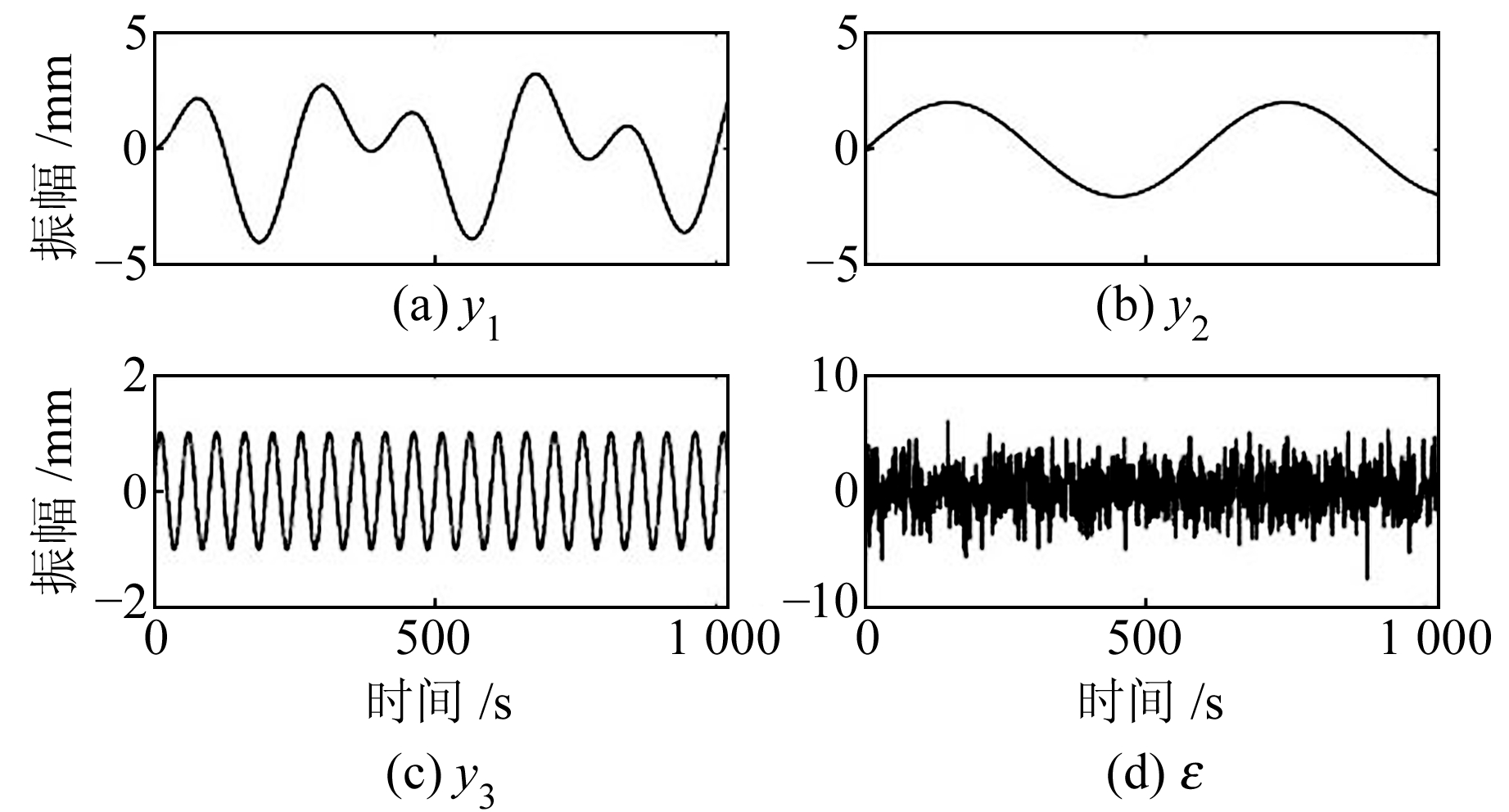
2 模拟数据降噪分析 2.1 模拟数据1GPS坐标时间序列一般由季节项、趋势项与噪声3部分组成,模拟数据1先剔除了站点位置、趋势项及阶跃式偏移,主要考虑3个恒定振幅的周期项和高斯白噪声。模拟数据1设置采样频率为1 Hz,采样点数为1 024个,并加入信噪比为4 dB的高斯白噪声(Noise),其构成分量的信号波形如图 1所示。模拟数据1的表达式为:
|
图 1 构成模拟信号的各分量信号波形 Fig. 1 Waveforms of components constituting analog signals |
| $ \left\{\begin{array}{l} {y_{1}=4 \sin \left(\frac{2 \pi t}{800}\right) \sin \left(\frac{2 \pi t}{250}\right)} \\ {y_{2}=2 \sin \left(\frac{2 \pi t}{600}\right)} \\ {y_{3}=\sin \left(\frac{2 \pi t}{50}\right)} \\ {\varepsilon=\text { Noise }} \\ {x=y_{1}+y_{2}+y_{3}+\varepsilon} \end{array}\right. $ | (5) |
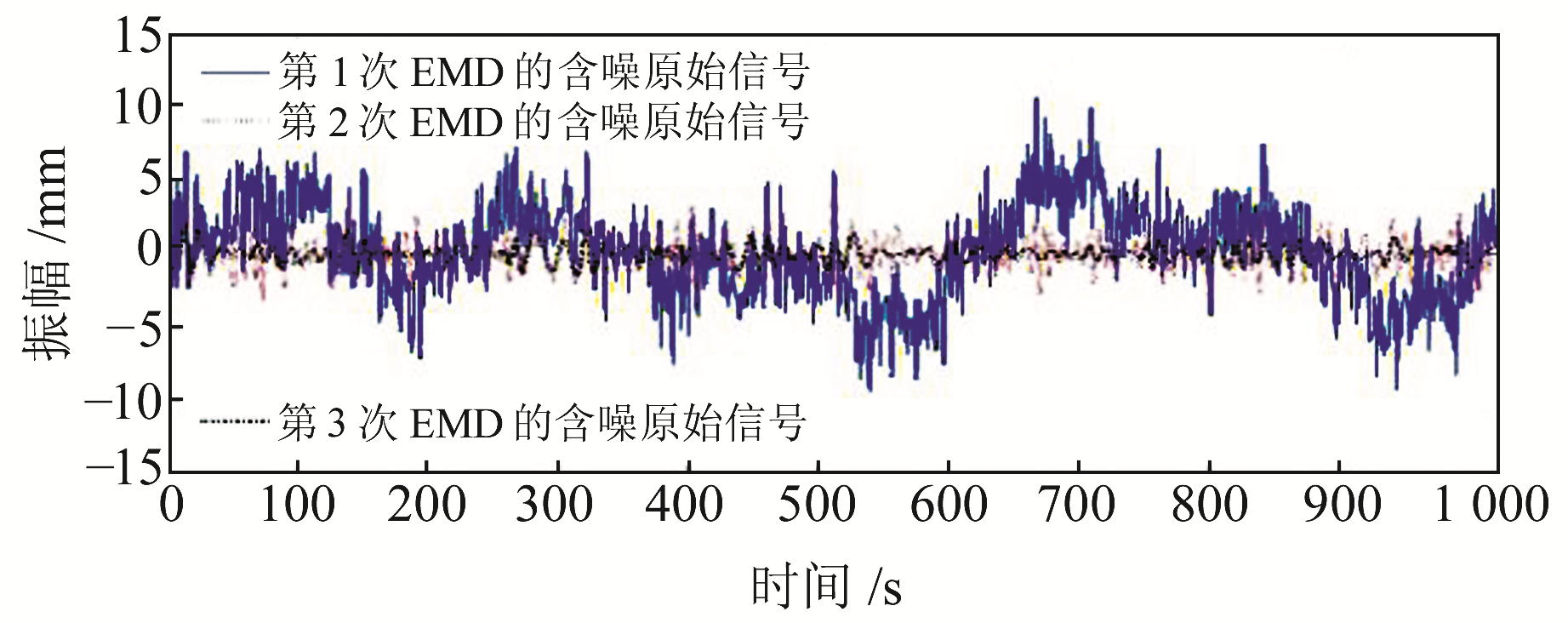
利用改进的EMD方法对模拟数据1进行分解,得到3次EMD的含噪原始信号的波形如图 2所示。从图 2中可以看出,第2次EMD的原始信号振幅在某些点位较大,所去掉的高频噪声中含有“真实”信号,第3次EMD的原始信号波形与白噪声的分布规律符合较好。图 3为每次EMD的各IMF分量与原始信号的相关系数,取每次分解中相关系数第1次到达局部极小值的点作为分界IMF分量。由图 3可知,第1次EMD中,第3个IMF分量为分界IMF分量;第2次、第3次EMD中,第4个IMF分量为分界IMF分量。
|
图 2 3次EMD的含噪原始信号 Fig. 2 Noisy raw signals decomposed by each EMD |

|
图 3 3次EMD的互相关系数 Fig. 3 The correlation coefficients decomposed by each EMD |
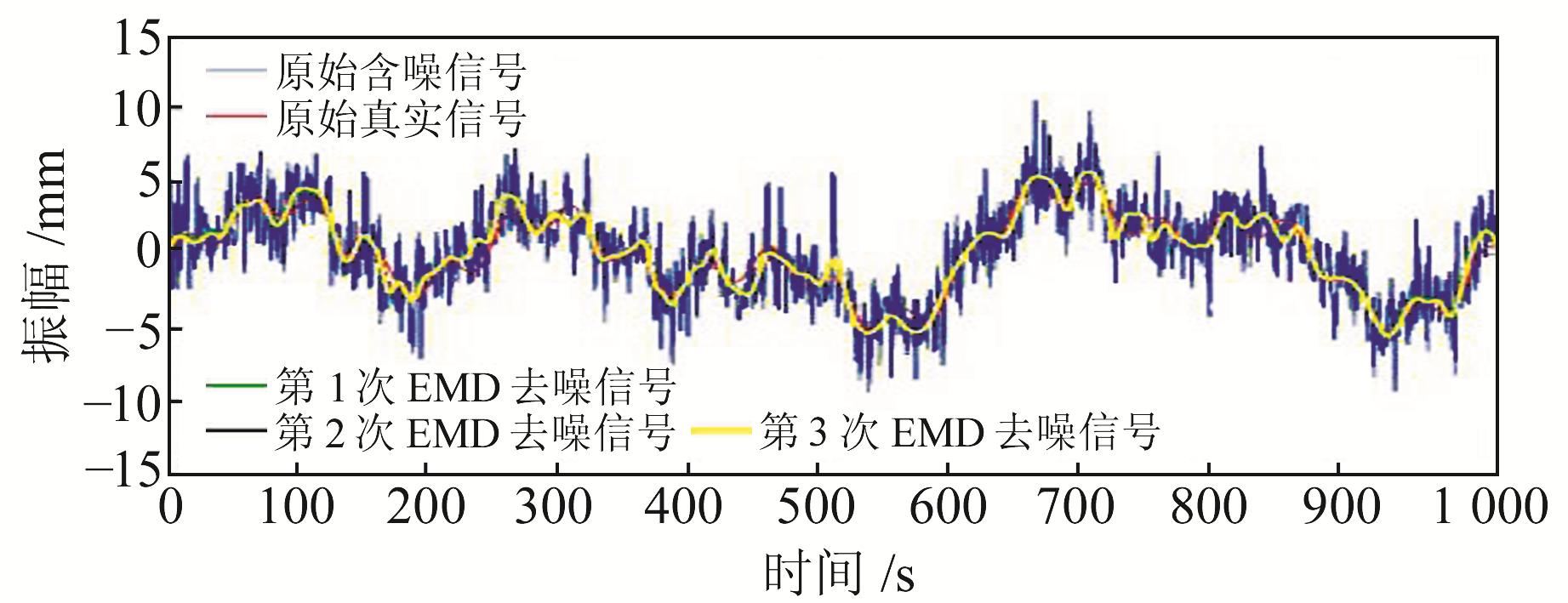
为验证本文方法的优势,将传统EMD方法与本文改进的EMD方法进行对比分析。在传统的EMD方法中,将第1次EMD的IMF1、IMF2、IMF3分量直接视为高频噪声,剩余的IMF分量进行重构,得到降噪后的信号;而改进的EMD方法从前1次EMD的高频噪声中再次获取“真实”信号,避免“真实”信号被“湮没”。2种方法所得到的降噪信号波形如图 4所示,由图可见,与模拟数据1相比,传统EMD方法与本文方法所得的降噪信号的波形明显更加光滑,说明2种方法都达到了降噪的效果;相比于传统EMD方法,本文改进的EMD方法所得的降噪信号波形在波峰波谷处的幅值与真实信号的幅值更加接近,证明本文方法能够提取出传统EMD方法“湮没”的纯净信号,降噪精度更高。
|
图 4 原始时间序列与降噪时间序列 Fig. 4 Primitive time series and noise reduction time series |
为定量说明改进的EMD方法与传统EMD方法的去噪效果,引入相关系数、均方根误差及信噪比等评价指标,计算所得结果如表 1所示。由表可知,进行2次EMD的去噪效果比进行3次EMD的去噪效果更好,但降噪效果都优于传统的EMD方法。进行3次EMD所获得的降噪信号与传统的EMD获得的降噪信号相比,RMSE值减小了0.7%,相关系数提高了0.000 7,SNR值提高了约0.29 dB,表明本文方法确实能够提取高频IMF分量中的“真实”信号。
|
|
表 1 重构信号与真实信号的评价指标值 Tab. 1 Evaluation index value of reconstructed signals and real signals |
由于连续GPS坐标序列中含有振幅时变季节性信号,模拟数据2在剔除站点位置、趋势项及阶跃式偏移的前提下,加入了振幅变化因子[13]。通过下式模拟了10 a的坐标序列时变季节性信号模拟数据:
| $ \begin{array}{c} s\left(t_{i}\right) =a \sin \left(2 \pi t_{i}\right)+b \cos \left(2 \pi t_{i}\right)+c\left(t_{i}\right) \sin \left(2 \pi t_{i}\right)+\\ c\left(t_{i}\right) \cos \left(2 \pi t_{i}\right) +d \sin \left(4 \pi t_{i}\right)+e \cos \left(4 \pi t_{i}\right)+\\ c\left(t_{i}\right) \sin \left(4 \pi t_{i}\right)+c\left(t_{i}\right) \cos \left(4 \pi t_{i}\right)+\varepsilon\left(t_{i}\right) \end{array} $ | (6) |
式中,s(ti)为模拟的时变季节性信号数据,a、b、d、e为常数(本文取a=2 mm,b=3 mm,d=4 mm,e=5 mm),ti为GPS年积日,c(ti)=2e0.3 sin(ti)为振幅变化因子,ε(ti)为噪声(模拟数据2中加入信噪比为6 dB的高斯白噪声)。图 5为依据式(6)仿真的数据,其中图 5(a)、5(b)分别为年周期信号与半周年信号,图 5(c)为时变年周期信号与时变半周年信号叠加构成的真实季节性信号,图 5(d)为模拟的含噪季节性信号。

|
图 5 带有周期信号的坐标序列模拟数据 Fig. 5 Coordinate sequence analog data with periodic signals |
对模拟数据2共进行了3次EMD,每次EMD计算的互相关系数如表 2所示,其中“NaN”表示空值,P1、P2、P3分别表示第1次、第2次、第3次EMD的各IMF分量与原始模拟数据的互相关系数。由表 2可知,第1次EMD时,IMF3分量与原始模拟数据的互相关系数取得第1次局部极小值,即IMF3分量为分界IMF分量;第2次EMD时,IMF4分量为分界IMF分量;第3次EMD时,IMF8分量为分界IMF分量。
|
|
表 2 3次EMD的互相关系数 Tab. 2 The correlation coefficients decomposed by each EMD |
将真实信号与每次EMD获得的降噪信号进行对比来验证本文方法的可靠性,结果如图 6所示。将图 6中标有数字的4处红色椭圆区域内图形放大可以发现,与第1次EMD的降噪信号相比,第2次、第3次EMD的降噪信号的振幅与真实信号振幅明显更为接近,峰值拟合效果更好,在其他区域差别不大。这一结果表明,本文改进的EMD方法比传统EMD方法的降噪效果更好,能够获取传统EMD方法中被“湮没”的真实信号。

|
图 6 真实模拟信号与3次EMD的降噪信号 Fig. 6 Real analog signals and noise reduction signals by EMD |
对模拟数据2分别计算了去噪信号与真实信号的互相关系数、均方根误差及信噪比,以定量说明本文方法与传统EMD方法的去噪效果,评价指标如表 3所示。由表可知,进行2次EMD的去噪效果比进行3次EMD的去噪效果更好,且二者都比传统EMD方法的降噪效果要好。进行3次EMD所获得的降噪信号相较于传统的EMD获得的降噪信号,RMSE值减小了0.13%,相关系数提高了0.000 1,SNR值提高了约0.025 dB,说明本文方法的降噪效果更佳,验证了本文方法对时变季节性信号降噪的可靠性。
|
|
表 3 重构信号与真实信号的评价指标值 Tab. 3 Evaluation index value of reconstructed signals and real signals |
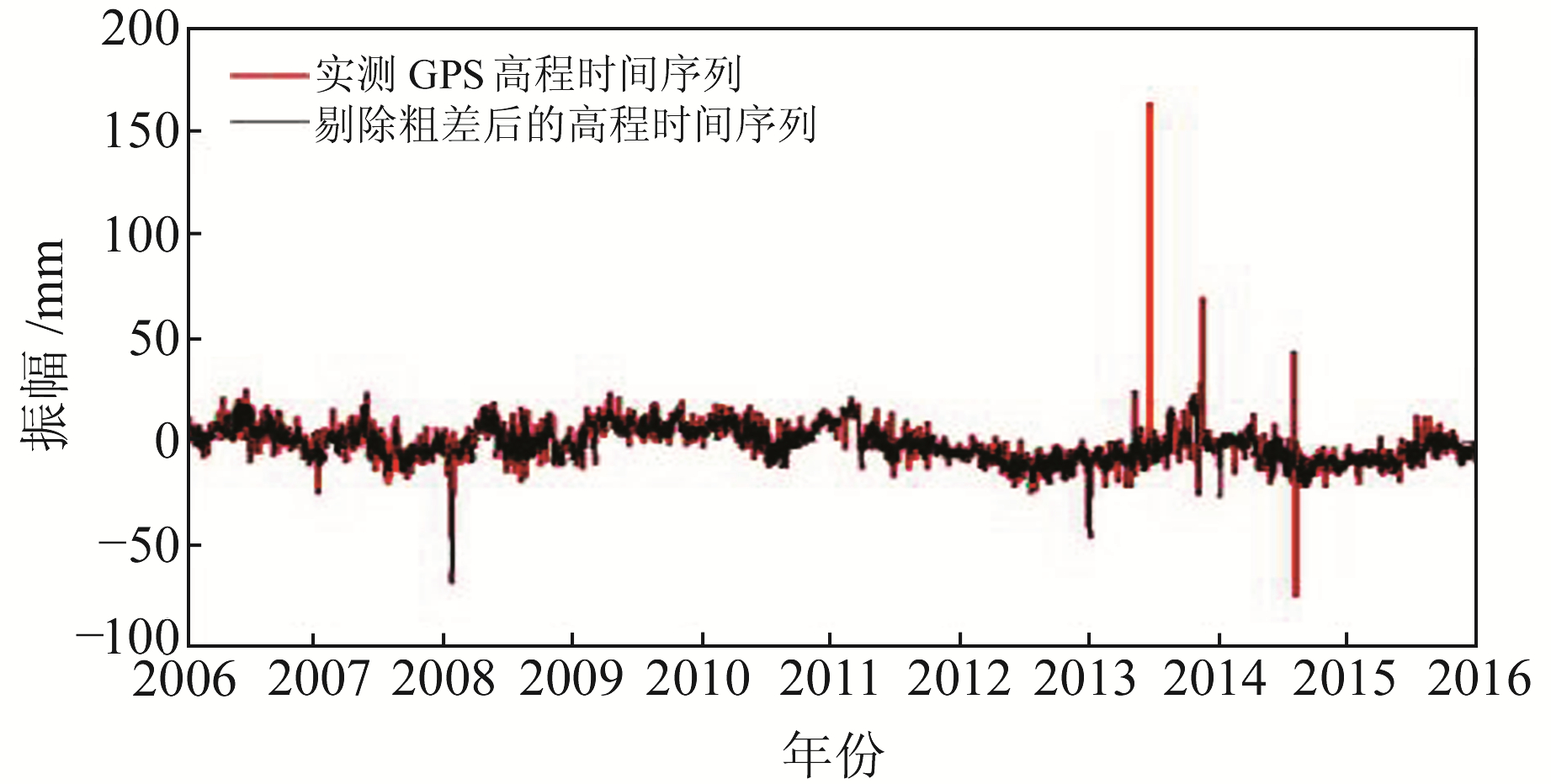
本文使用武汉(WUHN)站的实测高程(U)时间序列来进行降噪研究与分析。数据来源于中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn/),所取数据为该站点2006~2016年的高程时间序列,采样间隔为1/365.25 a,最大采样频率为365.25 Hz。由于实测数据中含有粗差,进行分析之前利用Hector软件对时间序列中较大的粗差进行剔除,作为本文降噪分析的原始数据序列,所得结果如图 7所示。由图可见,在一些时刻,剔除粗差后的时间序列的波动明显小于实测信号的波动,达到了很好的剔除粗差效果。
|
图 7 WUHN站实测GPS高程时间序列 Fig. 7 Elevation time series of WUHN station |
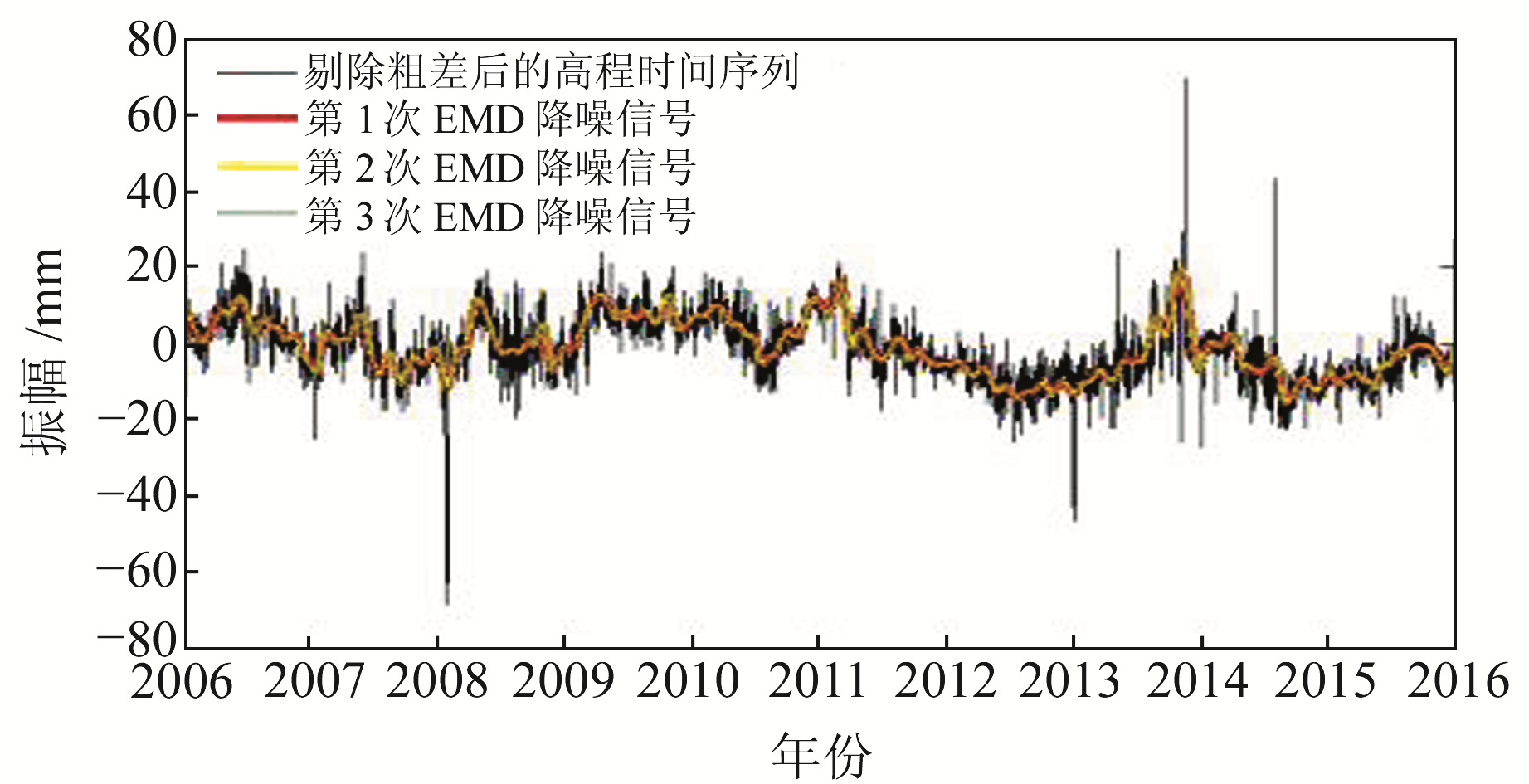
分析表 4可知,第1次EMD时,各IMF分量与原始数据的互相关系数第1次取得的极小值为0.188 5,对应的IMF4分量为分界IMF分量;第2次EMD时,互相关系数第1次取得的极小值为0.027 6,对应的IMF6分量为分界IMF分量;第3次EMD时,-0.030 9为相关系数第1次取得的极小值,对应的IMF6分量为分界IMF分量。综合表 4,图 8绘制了剔除粗差之后的GPS高程时间序列信号与每次EMD获得的降噪信号。由图 8可见,每次EMD降噪后的信号波形都非常平滑,说明本文方法与传统EMD方法都达到了去噪的目的。
|
|
表 4 每次EMD的互相关系数 Tab. 4 The correlation coefficients are decomposed by each EMD |
|
图 8 WUHN站实测GPS高程时间序列与每次EMD降噪信号 Fig. 8 GPS elevation time series and EMD noise reduction signals at WUHN station |
表 5计算了重构信号与原始高程时间序列的RMSE、P、SNR等单一评价指标值及复合评价指标T值。由表可见,RMSE与P的指标表明,改进的EMD方法降噪效果优于传统的EMD方法,但SNR指标却得出相反的结论,可知针对真值未知的实测数据,单一评价指标不能有效地评价降噪效果。而复合评价指标T综合考虑信号的细节信息和逼近信息,T为0时的降噪效果优于T为0.099 2和1时,即经3次EMD的降噪效果优于经2次EMD的降噪效果,且二者降噪效果均优于传统EMD方法,说明本文方法的降噪结果更可靠。
|
|
表 5 重构信号与实测GPS高程信号的评价指标值 Tab. 5 Evaluation index value of reconstructed signals and measured GPS elevation signals |
本文针对传统EMD方法在降噪过程中直接将分界IMF分量归入高频噪声,造成真实信号被“湮没”、去噪精度较低的问题,提出一种改进的EMD降噪方法。该方法是在传统EMD方法的基础上,对每次EMD得到的第2个IMF分量至分界IMF分量进行重构,将重构得到的信号视为下一次EMD的原始信号,最终累加所有EMD的低频IMF分量,得到降噪信号。与传统EMD方法相比,改进的EMD方法降噪精度更高。
本文使用了2组模拟数据与1组实测数据进行实验,结果表明,改进的EMD方法能够有效提取高频噪声中被“湮没”的“真实”信号,去噪精度优于传统的EMD方法,验证了改进的EMD方法的可靠性。然而,在实验过程中只进行了3次EMD,且模拟实验数据结果中,经2次EMD的降噪精度优于经3次EMD的降噪精度,与实测数据所得结果相反。考虑到过分解与欠分解问题,下一步需要对改进的EMD方法进行EMD次数的研究,确保去噪精度达到最优。
| [1] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [2] |
张双成, 李振宇, 何月帆, 等. GNSS高程时间序列周期项的经验模态分解提取[J]. 测绘科学, 2018, 43(8): 80-84 (Zhang Shuangcheng, Li Zhenyu, He Yuefan, et al. Extracting of Periodic Component of GNSS Vertical Time Series Using EMD[J]. Science of Surveying and Mapping, 2018, 43(8): 80-84)
(  0) 0) |
| [3] |
胡爱军, 孙敬敬, 向玲. 经验模态分解中的模态混叠问题[J]. 振动、测试与诊断, 2011, 31(4): 429-434 (Hu Aijun, Sun Jingjing, Xiang Ling. Mode Mixing in Empirical Mode Decomposition[J]. Journal of Vibration Measurement and Diagnosis, 2011, 31(4): 429-434 DOI:10.3969/j.issn.1004-6801.2011.04.006)
(  0) 0) |
| [4] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition:A Nosie-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
(  0) 0) |
| [5] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [6] |
罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报:信息科学版, 2012, 37(4): 450-453 (Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 450-453)
(  0) 0) |
| [7] |
梁喆, 彭苏萍, 郑晶. 基于EMD和互信息熵的微震信号自适应去噪[J]. 计算机工程与应用, 2014, 50(4): 7-11 (Liang Zhe, Peng Suping, Zheng Jing. Self-Adaptive Denoising for Microseismic Signal Based on EMD and Mutual Information Entropy[J]. Computer Engineering and Application, 2014, 50(4): 7-11 DOI:10.3778/j.issn.1002-8331.1307-0287)
(  0) 0) |
| [8] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 311-321 (Jia Ruisheng, Zhao Tongbin, Sun Hongmei, et al. Micro-Seismic Signal Denoising Method Based on Empirical Mode Decomposition and Independent Component Analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 311-321 DOI:10.3969/j.issn.1672-7940.2015.03.006)
(  0) 0) |
| [9] |
肖小兵, 刘宏立, 马子骥. 基于奇异谱分析的经验模态分解去噪方法[J]. 计算机工程与科学, 2017, 39(5): 919-924 (Xiao Xiaobing, Liu Hongli, Ma Ziji. An Empirical Mode Decomposition De-Noising Method Based on Singular Spectrum Analysis[J]. Computer Engineering and Science, 2017, 39(5): 919-924 DOI:10.3969/j.issn.1007-130X.2017.05.015)
(  0) 0) |
| [10] |
曲从善, 路廷镇, 谭营. 一种改进型经验模态分解及其在信号消噪中的应用[J]. 自动化学报, 2010, 36(1): 67-73 (Qu Congshan, Lu Tingzhen, Tan Ying. A Modified Empirical Mode Decomposition Method with Applications to Signal Denoising[J]. Acta Automatica Sinica, 2010, 36(1): 67-73)
(  0) 0) |
| [11] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1248-1252 (Zhang Shuangcheng, He Yuefan, Li Zhenyu, et al. EMD for Noise Reduction of GPS Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1248-1252)
(  0) 0) |
| [12] |
朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报:信息科学版, 2015, 40(5): 688-694 (Zhu Jianjun, Zhang Zhetao, Kuang Cuilin, et al. A Reliable Evaluation Indicator of Wavelet De-Noising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 688-694)
(  0) 0) |
| [13] |
卢辰龙, 匡翠林, 戴吾蛟, 等. 采用变系数回归模型提取GPS坐标序列季节性信号[J]. 大地测量与地球动力学, 2014, 34(5): 94-100 (Lu Chenlong, Kuang Cuilin, Dai Wujiao, et al. Extracting Seasonal Signals from Continuous GPS Time Series Based on Varying-Coefficient Regression Models[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 94-100)
(  0) 0) |
2. School of Civil Engineer and Architecture, East China Jiaotong University, 808 East-Shuanggang Street, Nanchang 330013, China;
3. State Key Laboratory of Rail Transit Engineering Informatization, China Railway First Survey and Design Institute Group Co Ltd, 2 Xiying Road, Xi'an 710043, China
 2020, Vol. 40
2020, Vol. 40


