2. 厦门市万科房地产有限公司,厦门市莲前西路859号,361000
微动探测方法指通过采集微动数据,然后进行数据处理提取瑞雷波频散曲线,最后反演获得S波速度结构的浅层地球物理勘探方法[1-4]。微动勘探方法在国内外逐渐应用于诸多工程与地球物理领域,取得了良好的效果。Scherbaum等[5]利用单台和台阵技术测出了德国科隆市浅层S波速度剖面。丁连靖和冉伟彦[6]利用F-K法探测浅部横波速度结构,证实该原理的可靠性,并提出随机布阵的野外观测方法。徐佩芬等[7-9]运用微动探测方法在陷落柱、孤石、地热、隐伏断裂探测等方面开展工作。李娜[10]提出在同一直线台阵上开展微动探测和人工源面波联合勘探的数据采集处理方法,弥补了直线形台阵高频段的不足。Yamanaka[11]利用微动探测方法,对Kumamoto地震后场地进行了地层调查。杜亚楠等[12]在衡阳用三重圆形观测台阵探测滑坡体,解释滑动面埋深,圈出滑坡体块石。
微动探测现今广泛应用于工程实践中,学者以及技术人员大多采用单一的圆形或嵌套三角形等台阵观测,形式较单一,采用组合台阵形式以及对比实验的观测研究较少。本文将微动勘探不同台阵形式的探测效果进行对比,探讨可行、效率高和便于野外施工的微动探测台阵形式。在江汉盆地沉降中心区的同一场地分别用三重圆形、T形及L形3种常见的台阵进行野外观测实验,并对各组台阵数据使用空间自相关法提取相应的频散曲线,再通过反演获取测区地下速度结构模型,并与地震观测孔地层结果进行对比,以便得到最优的野外观测台阵形式。
1 微动与微动探测方法 1.1 空间自相关法微动指地球上每时每刻都存在着由非地震引起的微小振动[13]。微动信号的振幅很小,通常在10-4~10-2 mm之间,人类无法感知,但能被高精度地震仪接收。微动是由体波和面波组成的振动,信号成分很复杂,并且瑞雷波的能量占信号总能量的70%以上。早期微动被认为是一种噪声源,因此微动也被称为背景噪声,许多学者在消除微动对地震学研究的影响方面开展了很多工作。随着对浅层面波的研究越来越深入,微动也逐渐被用来作为瑞雷波的天然振源。通过野外采集微动信号,可从微动信号中提取频散曲线来反演地下地层结构。目前常用的方法是空间自相关法。
空间自相关法(spatial auto-correlation method, SPAC)最早由Aki提出[14]。Aki认为,微动在时间上、空间上随机分布,同时在一定时间段内具有稳定性。因此认为微动是一种平稳随机过程,而获取的一段时间内的微动信号数据可看成是稳定随机过程的样本函数。为了便于接收来自实验场地任意方向的微动信号,SPAC法中台阵常布设成嵌套三角形或者圆形。为了克服这个局限,Ling和Okada提出了扩展的空间自相关法(extended spatial auto-correlation method, ESPAC),允许台阵形式多样化,例如T形、L形以及十字形等形式。
假设在两个不同的点A、B进行微动观测,A、B的位置矢量分别为η、η + ξ,那么A点记为X(t, η),B点记为X(t, η + ξ)。对于A、B两点同时得到的记录,将其空间自相关函数S(t, η, ξ)定义为:
| $ S\left( {t, \mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}} \right) = E\left[ {{X^ * }\left( {t, \mathit{\boldsymbol{\eta }}} \right)X\left( {t, \mathit{\boldsymbol{\eta }} + \mathit{\boldsymbol{\xi }}} \right)} \right] $ | (1) |
则可得:
| $ S\left( {\bf{ \pmb{\mathsf{ ξ}} }} \right) = \int {\int {\int_{ - \infty }^{ + \infty } {\exp ik\mathit{\boldsymbol{\xi }}} \cdot E\left[ {{{\left| {{\rm{d}}z\left( {\omega ,k} \right)} \right|}^2}} \right]} } $ | (2) |
可以发现,自相关函数变成位置矢量ξ的函数。因为一般讨论瑞雷波的基阶振型,k是ω的单值函数,式(1)可以改写成:
| $ \begin{array}{*{20}{l}} {\;\;\;\;S\left( {r, \theta } \right) = }\\ {\int_{ - \infty }^{ + \infty } {\int_0^{2\pi } {\left[ {\exp \left( {ikr\cos \left( {\theta - \varphi } \right)} \right)h\left( {\omega , \varphi } \right){\rm{d}}\varphi } \right]} } {\rm{d}}\omega } \end{array} $ | (3) |
令空间协方差函数g(ω, r, θ)为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;g\left( {\omega , r, \theta } \right) = \\ \int_0^{2\pi } {\exp \left( {ikr\cos \left( {\theta - \varphi } \right)} \right)h\left( {\omega , \varphi } \right){\rm{d}}\varphi } \end{array} $ | (4) |
则有:
| $ S\left( {r, \theta } \right) = \int_{ - \infty }^{ + \infty } {g\left( {\omega , r, \theta } \right)} {\rm{d}}\omega $ | (5) |
微动探测法有多种观测台阵形式,但对于不同台阵形式,理论分析和实验结果尚缺乏相关的对比研究,而圆周密布采集器进行观测又不太现实。为了提高野外实验工作效率,本文使用三重圆形、L形及T形3种台阵形式进行观测实验。利用该3种台阵形式的简化理论模型进行微动数据的采集,通过对比分析3组数据结果,探讨3种不同台阵形式对微动结果的影响。
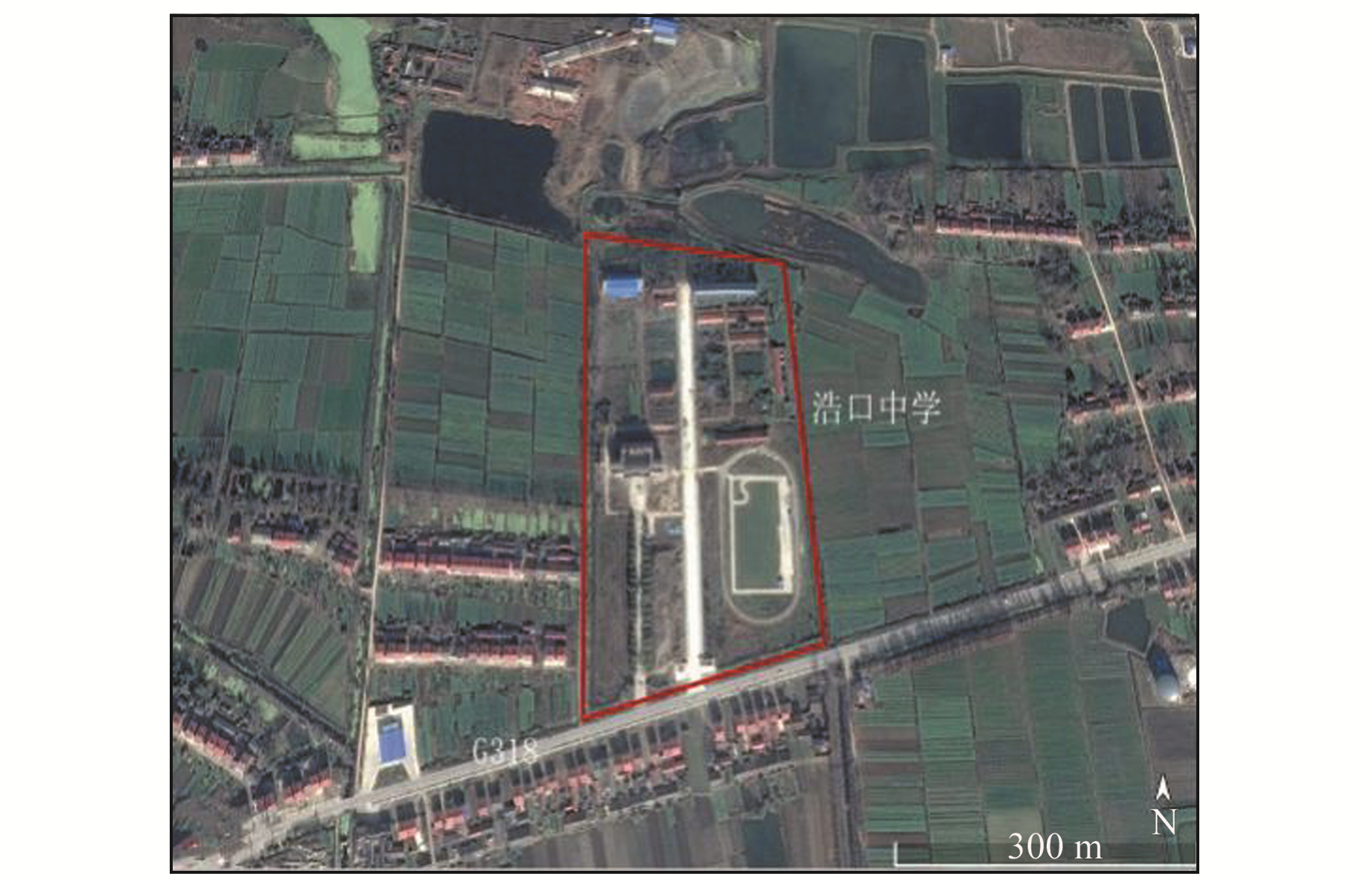
2 数据采集和分析 2.1 实验场地本文选取潜江市浩口镇浩口中学(30°23′36″N,112°39′39″E)作为野外实验观测场地。浩口中学位于潜江市浩口镇东北方向,距离镇中心约2.5 km,G318国道北侧。浩口中学整体近南北走向,长约400 m,宽约250 m。学校大门在南面,外侧是公路,其余3面外侧大部分为农田、耕地(图 1)。
|
图 1 浩口中学GPS卫星图 Fig. 1 GPS satellite map of Haokou middle school |
野外观测时,采用的微动仪器的技术参数如表 1所示,其频带范围为1~100 Hz。采用GPS授时,确保台阵观测中不同仪器记录的同步性。选定的采样率为100 Hz,进行每个点有效同步观测时长不少于30 min。
|
|
表 1 微动仪器的技术参数 Tab. 1 Technical parameters of the microtremor instrument |
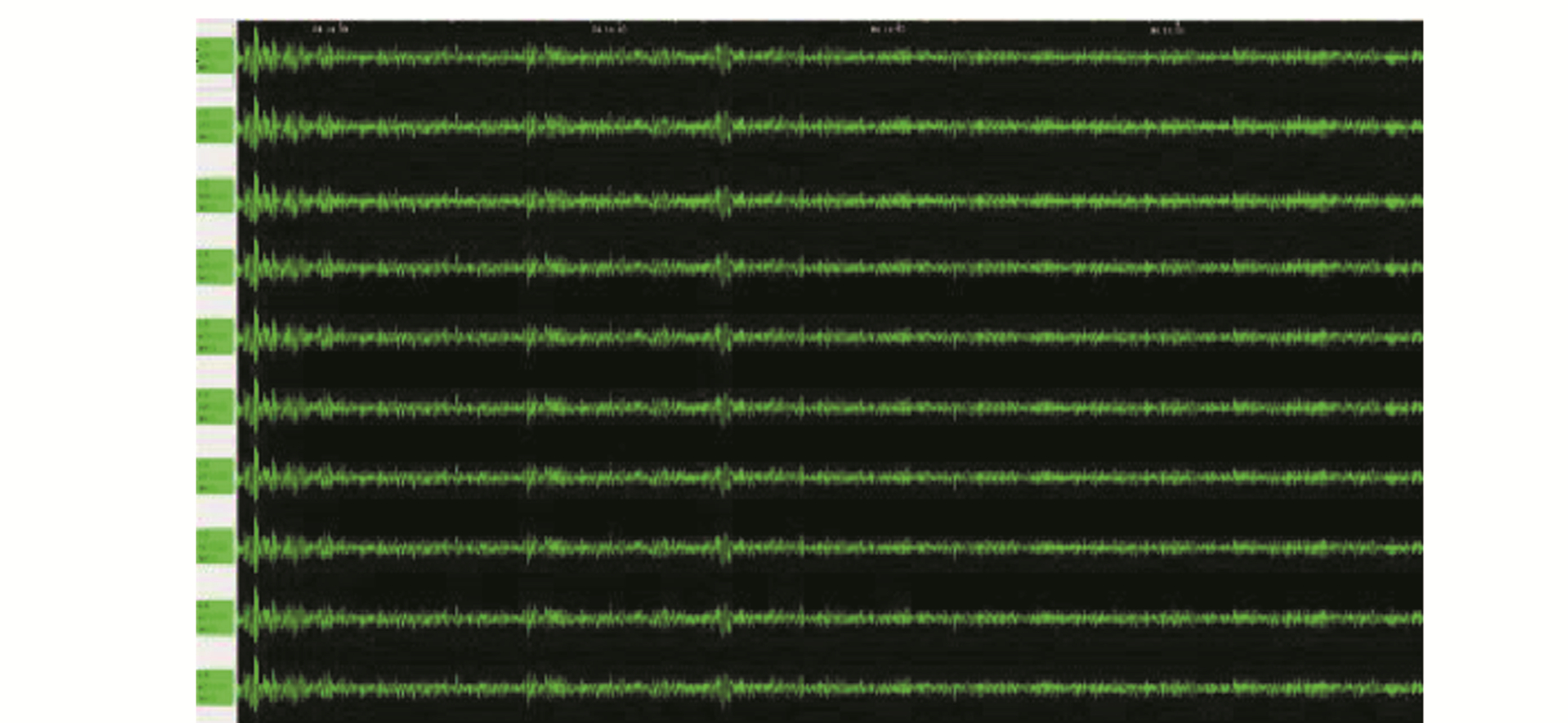
进行野外实验观测之前,仪器需要进行一致性检测,并对采集到的数据进行质量检查。10台仪器截取的部分时段数据如图 2所示,可以看到,波形几乎完全相同且无中断。对数据进行功率谱分析,仪器功率谱测试结果如图 3所示,结果表明,仪器在1~30 Hz内有着较好的一致性,证明本次10组仪器能满足微动探测要求。
|
图 2 仪器一致性测试波形记录 Fig. 2 Waveform records of instrument's conformance test |

|
图 3 仪器功率谱测试结果 Fig. 3 Test results of instrument's power spectrum |
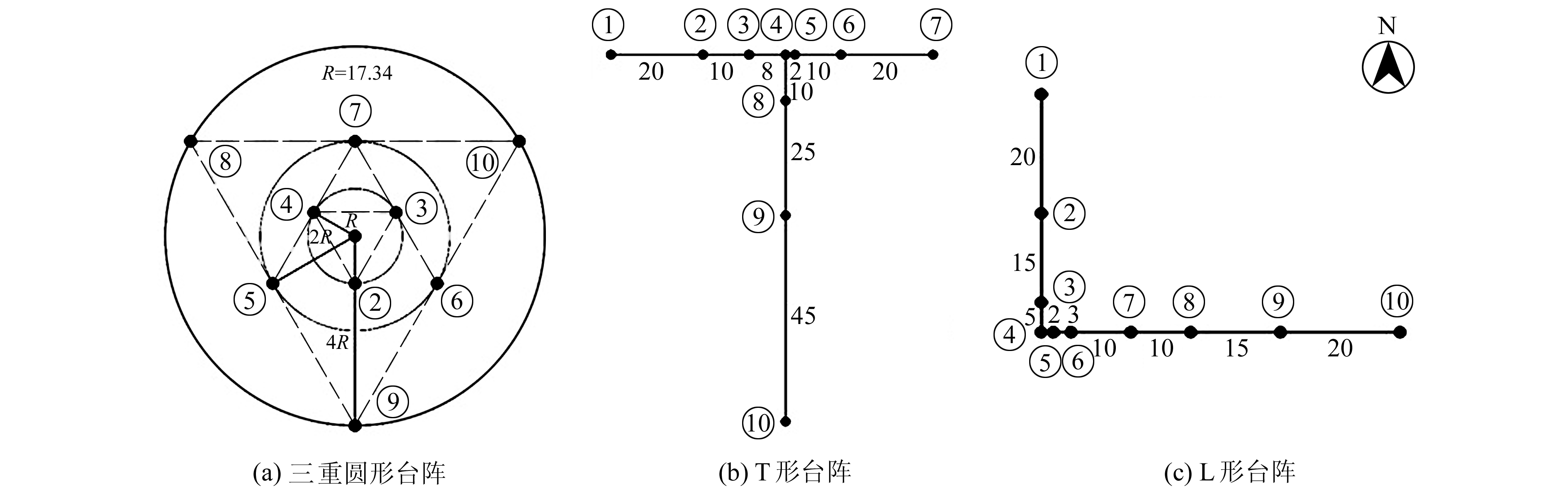
本文根据前期场地踏勘情况,采用了10台1~100 Hz地震仪,共设计3种台阵形式,在选定的场地内进行布设和观测。台阵布设方案如图 4(单位m)所示,图 4(a)为三重圆形台阵,其半径分别为17.32 m、34.65 m、69.28 m;图 4(b)为T形台阵,其两条边长分别为70 m、80 m;图 4(c)为L形台阵,其两条边长分别为40 m、60 m。
|
图 4 台阵测点布局 Fig. 4 The layout of arrays |
实验过程中,为保证台阵布设的位置精度,采用RTK(real-time kinematic)对台站位置精确定位。将台站位置确定好后架设仪器,并进行检查。在架设仪器过程中要确保仪器调平(要注意轻拿轻放)、电源与GPS连接牢固,最后在收集数据之前对每台仪器进行检查,确保电源接通,GPS授时正常。一切程序完成后,所有实验人员远离观测场地,并现场填写记录卡。根据现场实验条件,对每个观测点的观测时长为2 ~ 3.5 h。在3组实验过程中,实验时间主要是在早晨或者晚上,场地较为安静、无风。
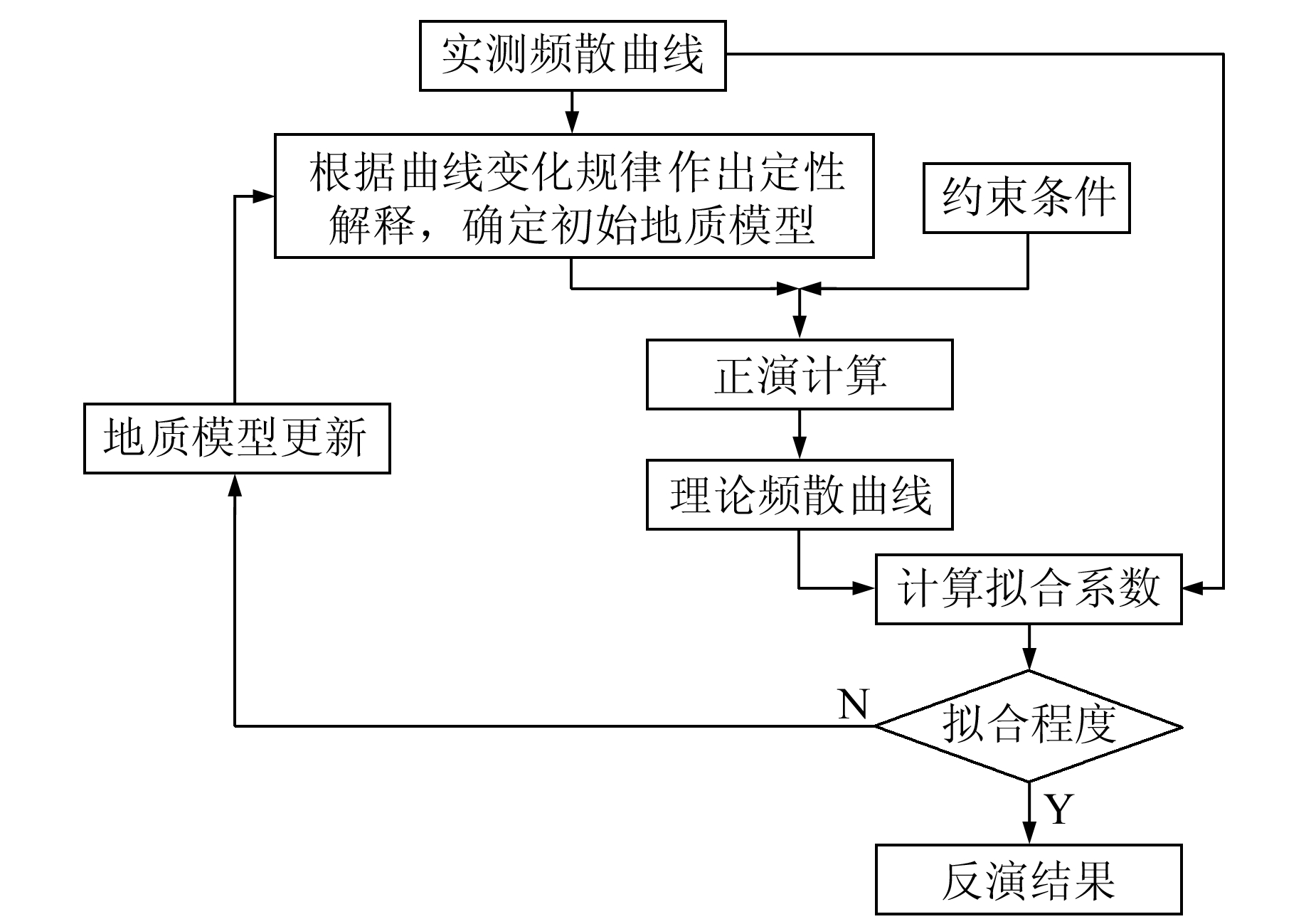
2.4 数据处理流程从微动信号记录获取的半径为r0的圆形台阵通过任何频率为f0的空间自相关系数ρ0,拟合第一类零阶贝塞尔函数,可获得与这些频率对应的相速度c(f0)。通过以上步骤便可得到整个微动数据的f-c频散点,将其进行光滑处理后,即可得到频散曲线[15]。根据曲线变化规律以及约束条件,给出定性解释,确定初始地质模型。通过正演计算获取理论频散曲线,然后计算拟合系数,根据拟合程度来获取反演结果。若拟合程度不高,则要建立优化地质模型。图 5为频散曲线反演S波速度结构流程图。
|
图 5 反演S波速度结构的流程 Fig. 5 Flow of inversion of S-wave velocity structure |
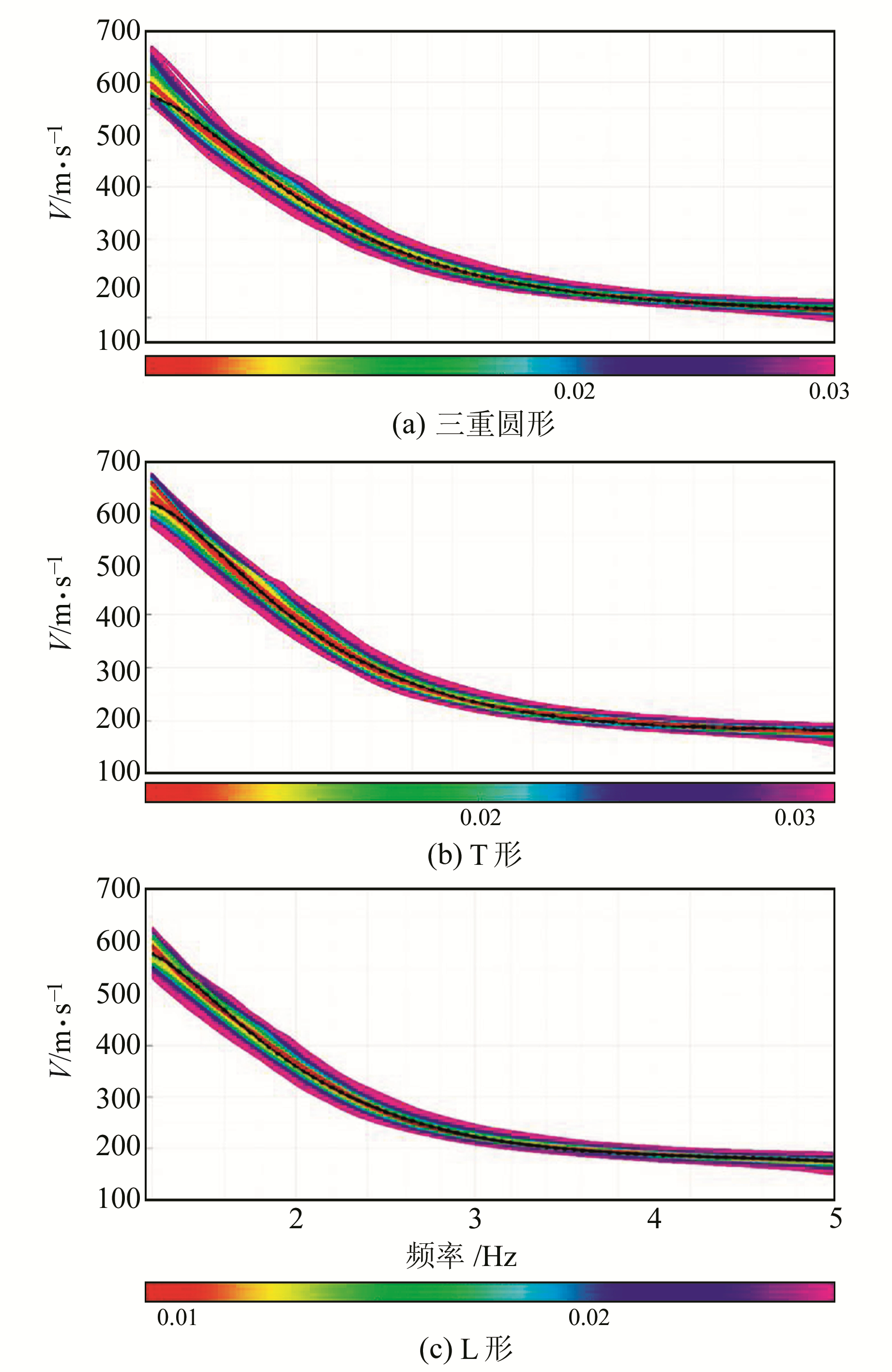
根据拟合效果来获取频散点,获取频散图谱,如图 6~8所示。由图可知,3组不同台阵形式的频散图谱有区别,但整体上是一致的。有效频段范围为1.2~4.6 Hz,其对应的相速度范围为200~600 m/s。结果表明,频散图谱能量集中度具有明显的差异,三重圆形台阵频散图谱能量集中度最高;L形、T形台阵在2.0~4.6 Hz频段范围内集中度也较高,而在1.2~2.0 Hz频段范围内较为分散。
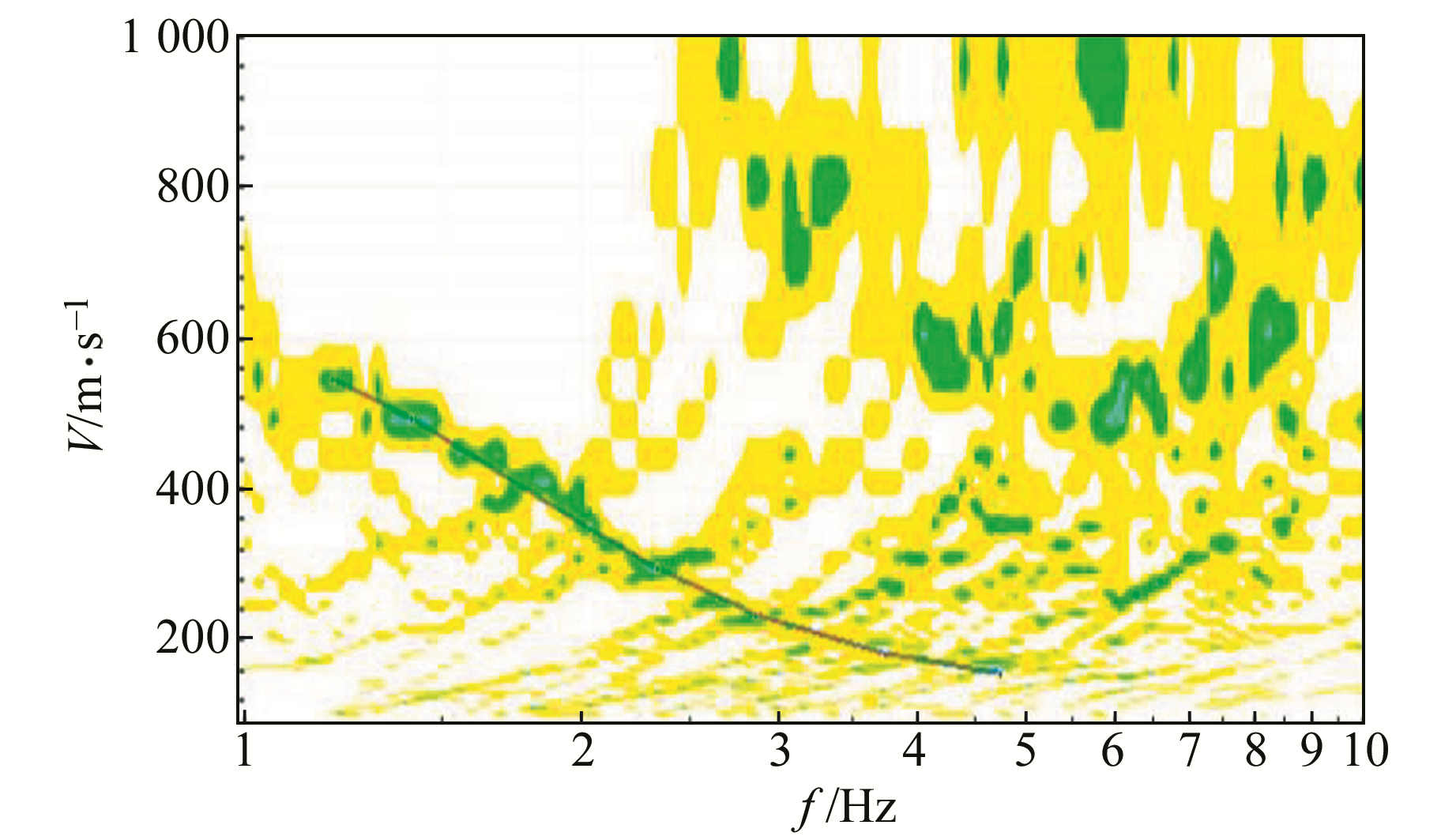
|
图 6 三重圆形台阵的频散图谱 Fig. 6 Dispersion spectrum of nested equilateral triangles array |
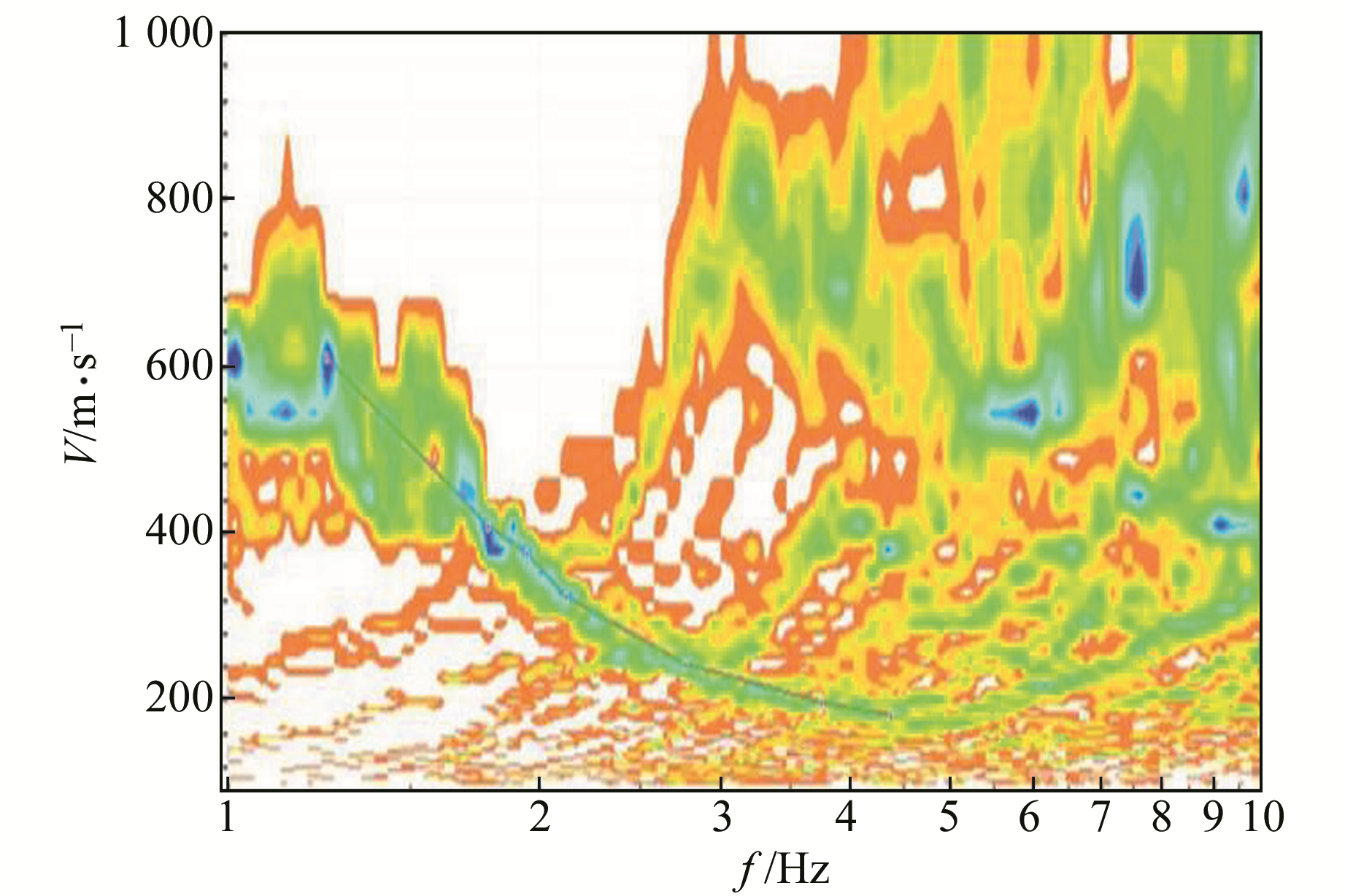
|
图 7 T形台阵的频散图谱 Fig. 7 Dispersion spectrum of T-shape array |
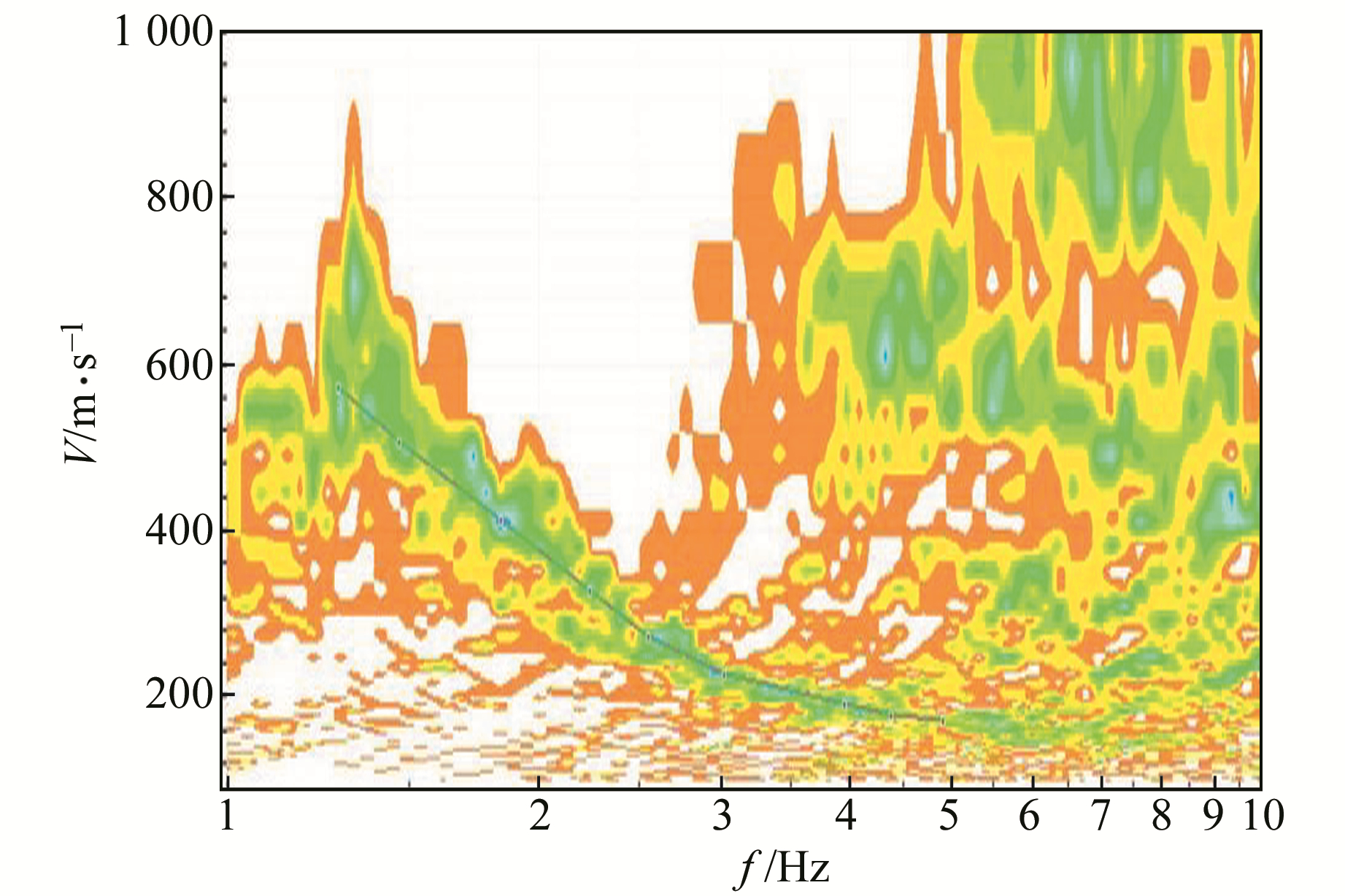
|
图 8 L形台阵的频散图谱 Fig. 8 Dispersion spectrum of L-shape array |
对所有台阵形式提取频散图谱,结果如图 9所示。
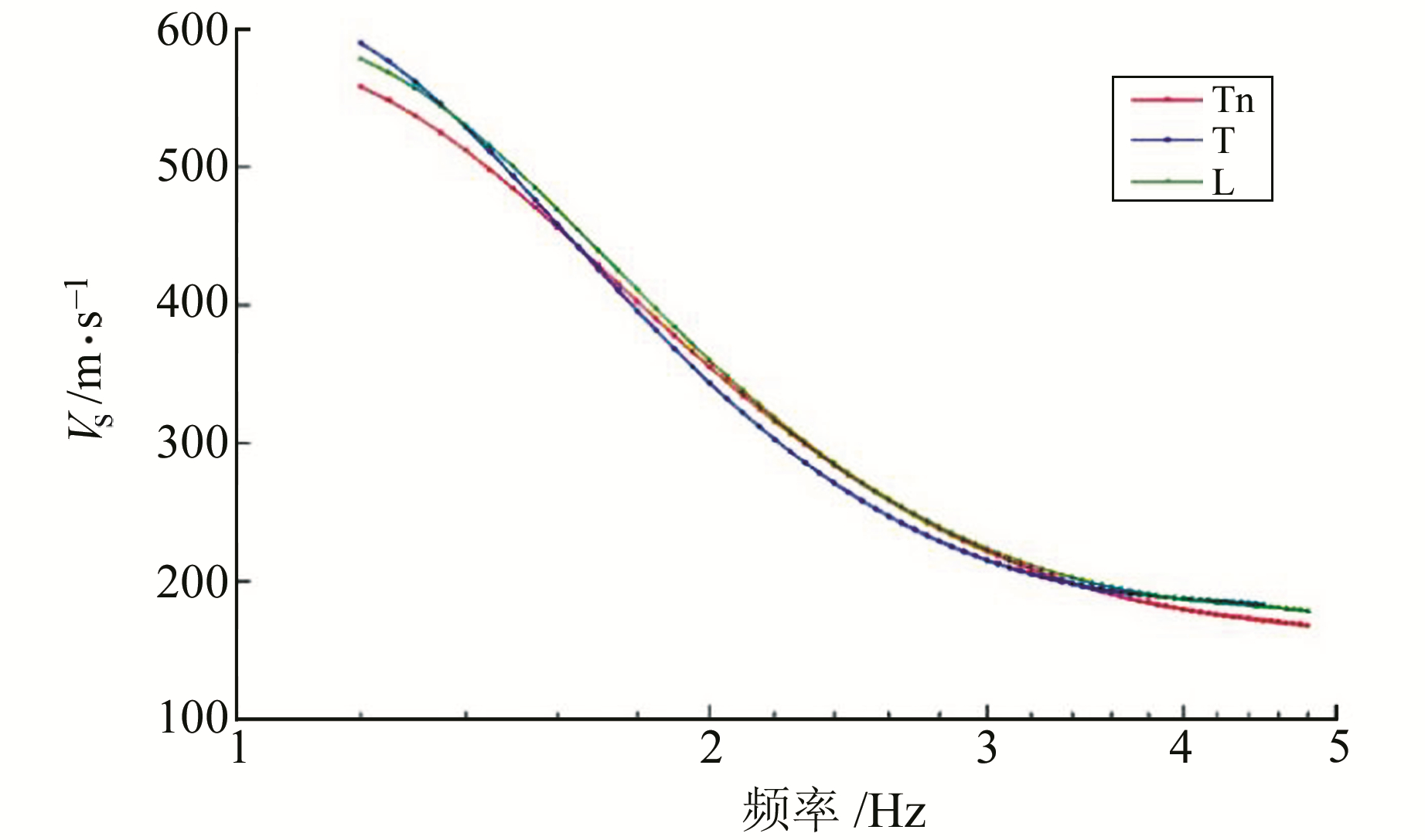
|
图 9 3种台阵频散曲线 Fig. 9 Dispersion curves for three arrays |
3组频散曲线拟合结果如图 10所示。整体来看,模型与3条频散曲线的拟合效果较好,残差值小于0.03。相比于低频段,高频段的拟合效果更好一些。
|
图 10 频散曲线拟合效果 Fig. 10 Dispersion curves for three arrays |
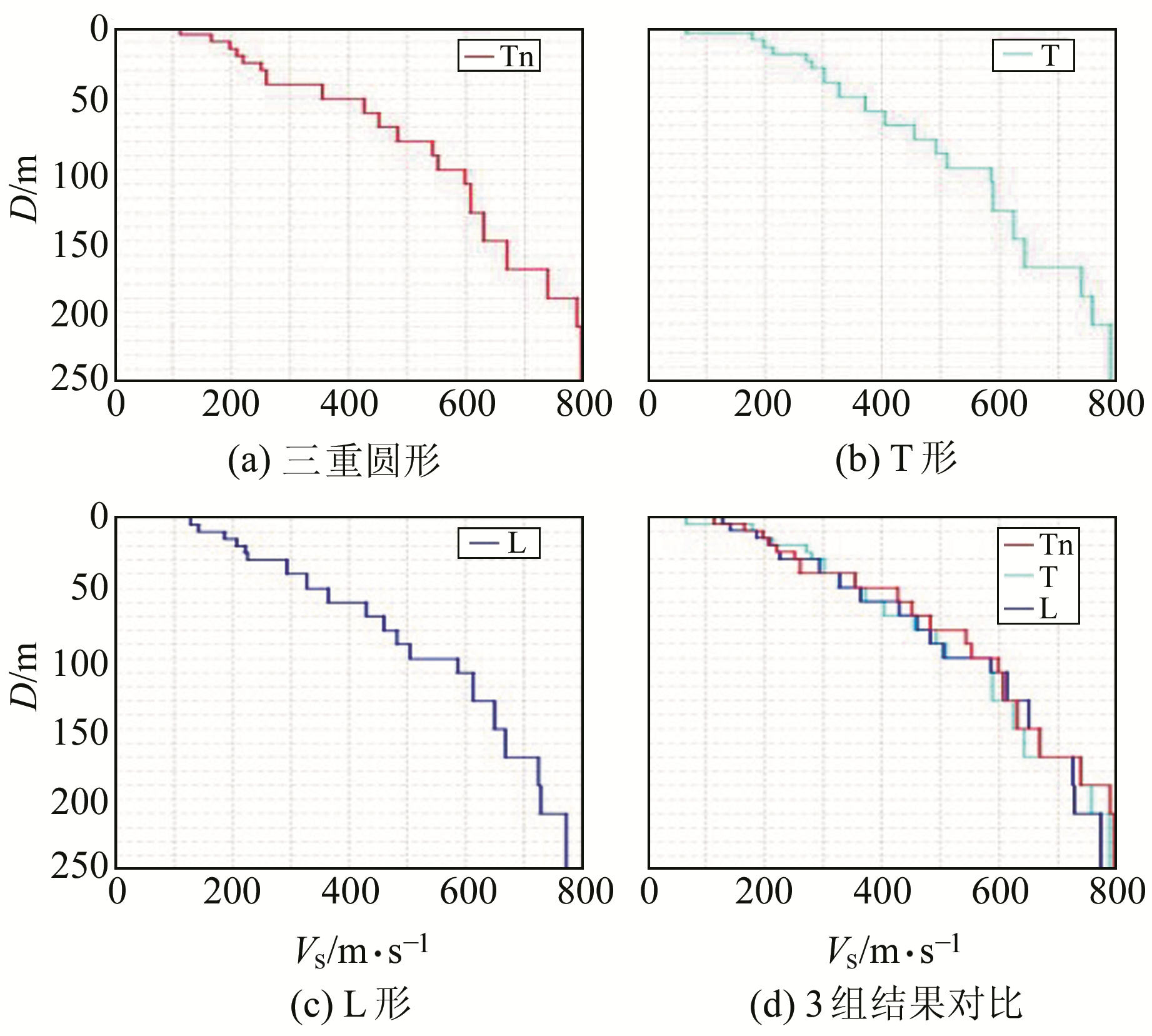
拟合的频散曲线与实际频散曲线一致,即可获得每条曲线的实际地层波速结构。将结果进行汇总,得到的横波速度结构如图 11所示。由图可知,3组横波速度结构变化趋势一致,而在某些深度区间内变化异常。将图中的横波速度结构进行简化,获得地层结构分界面深度结果(表 2)。
|
图 11 反演S波速度结构 Fig. 11 Inversion of S-wave velocity structure |
|
|
表 2 分界面深度情况 Tab. 2 The depth of interface |
由表可知,观测场地地层基本可以划分为5层。自上而下,第1层深度为10~20 m,分界面波速约为200 m/s;第2层深度为40~60 m,分界面波速约为350 m/s;第3层深度为80~100 m,分界面波速约为500 m/s;第4层深度为170~210 m,分界面波速约为750 m/s;第5层深度在210 m以下。
从瑞雷波半波长理论判断,在100~130 m范围内存在的分界面,也与表中第3层和第4层分界面相对应,并且第3层和第4层之间的岩性差异较其他地层更大。
3 结果和讨论根据湖北省地震局在浩口中学完成的潜江市地震观测与预警示范工程地震监测井项目,我们获取了该测区地层分布情况。通过对3种不同台阵形式微动数据的处理获取地层速度结构,并与潜江市地震监测井项目的钻孔资料进行对比分析(图 12)。
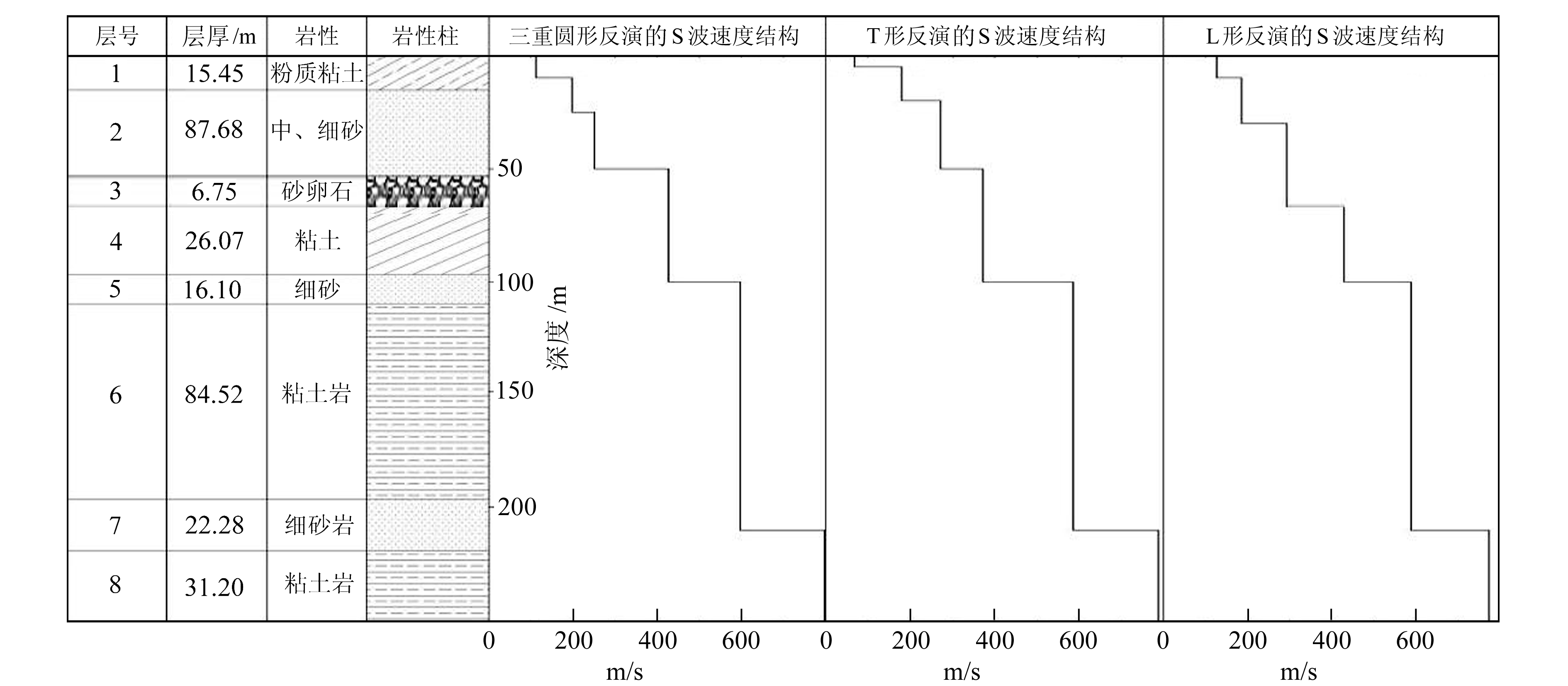
|
图 12 微动探测结果与钻孔岩芯对比 Fig. 12 Microtremor survey results compared with borehole core |
根据微动探测地层速度结构与钻探成果的对比,可以获得如下结论:
1) 从3组台阵都提取到了1.2~4.6 Hz内的频散曲线,且结果基本一致。
2) 频散图谱能量集中度具有明显的差异,三重圆形台阵频散图谱能量集中度最高,L形、T形台阵在2.0~4.6 Hz频段范围内集中度也较高,而在1.2~2.0 Hz频段范围内较分散。
3) 相比T形和L形台阵,三重圆形台阵在地层分界面处波速突变更明显,即三重圆形台阵比其他两种台阵形式的准确性及可靠性更高。
4 结语本文采用SPAC以及ESPAC法中常用的3种台阵形式,在江汉盆地浩口中学进行微动观测,获得不同台阵形式在地层结构探测中的结果,并与钻孔资料对比,获取实验结果及结论。由于L形以及T形台阵通常具有明显的方位指向性,抵抗不规则人为干扰的能力差,会影响频散谱的能量集中度,给相速度频散曲线的提取带来一定的误差。在宽阔、较平坦的场地条件下进行三重圆形探测,即使波场方向性较强,精度依然较高,探测结果较可靠;在场地局限的条件下,则只能采用L形、T形等台阵形式。根据前期在一些项目如某机场前、繁忙道路边的实际观测表明,只要有一定时长的稳定时段,精度还是基本能够满足要求,其台阵形式更为灵活有效。在实际工程应用中,应结合不同工程的探测要求以及不同场地条件,选取最合理的台阵形式进行观测,这也是将来值得深入研究的方向。
| [1] |
王振东. 微动的空间自相关法及其实用技术[J]. 物探与化探, 1986, 10(2): 123-133 (Wang Zhendong. The Micromotional Spatial Autocorrelation Method and Its Practical Technique[J]. Geophysical and Geochemical Exploration, 1986, 10(2): 123-133)
(  0) 0) |
| [2] |
沈雨忆, 李井冈, 王秋良, 等. 基于SPAC法勘探武汉市江夏区地下岩溶结构[J]. 大地测量与地球动力学, 2018, 38(5): 482-486 (Shen Yuyi, Li Jinggang, Wang Qiuliang, et al. Application of S-PAC Method to Probe Underground Karst Structure in Jiangxia District, Wuhan[J]. Journal of Geodesy and Geodynamics, 2018, 38(5): 482-486)
(  0) 0) |
| [3] |
孙勇军, 徐佩芬, 凌甦群, 等. 微动勘查方法及其研究进展[J]. 地球物理学进展, 2009(1): 326-334 (Sun Yongjun, Xu Peifen, Ling Suqun, et al. Microtremor Survey Method and Its Progress[J]. Progress in Geophys, 2009(1): 326-334)
(  0) 0) |
| [4] |
赵东. 被动源面波勘探方法与应用[J]. 物探与化探, 2010(6): 759-764 (Zhao Dong. Passive Surface Waves Methods and Applications[J]. Geophysical and Geochemical Exploration, 2010(6): 759-764)
(  0) 0) |
| [5] |
Scherbaum F, Hinzen K G, Ohrnberger M. Determination of Shallow Shear Wave Velocity Profiles in the Cologne, Germany Area Using Ambient Vibrations[J]. Geophysical Journal International, 2003, 152(3): 597-612 DOI:10.1046/j.1365-246X.2003.01856.x
(  0) 0) |
| [6] |
丁连靖, 冉伟彦. 天然源面波频率-波数法的应用[J]. 物探与化探, 2005(2): 139-141 (Ding Lianjing, Ran Weiyan. The Application of Natural Source Surface Wave Frequency-Waves Method[J]. Geophysical and Geochemical Exploration, 2005(2): 139-141)
(  0) 0) |
| [7] |
徐佩芬, 侍文, 凌甦群, 等. 二维微动剖面探测"孤石":以深圳地铁7号线为例[J]. 地球物理学报, 2012(6): 2 120-2 128 (Xu Peifen, Shi Wen, Ling Suqun, et al. Mapping Spherically Weathered"Boulders"Using 2D Microtremor Profiling Method: A Case Study Along Subway Line 7 in Shenzhen[J]. Chinese Journal of Geophysics, 2012(6): 2 120-2 128)
(  0) 0) |
| [8] |
徐佩芬, 李世豪, 杜建国, 等. 微动探测:地层分层和隐伏断裂构造探测的新方法[J]. 岩石学报, 2013(5): 1 841-1 845 (Xu Peifen, Li Shihao, Du Jianguo, et al. Microtremor Survey Method: A New Geophysical Method for Dividing Strata and Detecting the Buried Fault Structures[J]. Acta Petrologica Sinica, 2013(5): 1 841-1 845)
(  0) 0) |
| [9] |
徐佩芬, 李传金, 凌甦群, 等. 利用微动勘察方法探测煤矿陷落柱[J]. 地球物理学报, 2009(7): 1 923-1 930 (Xu Peifen, Li Chuanjin, Ling Suqun, et al. Mapping Collapsed Columns in Coal Mines Utilizing Microtremor Survey Methods[J]. Chinese Journal of Geophysics, 2009(7): 1 923-1 930)
(  0) 0) |
| [10] |
Yamanaka H, Chimoto K, Miyake H, et al. Observation of Earthquake Ground Motion due to Aftershocks of the 2016 Kumamoto Earthquake in Damageed Areas[J]. Earth Planets and Space, 2016, 68(1): 197 DOI:10.1186/s40623-016-0574-2
(  0) 0) |
| [11] |
李娜, 何正勤, 叶太兰, 等. 天然源面波勘探台阵对比试验[J]. 地震学报, 2015, 37(2): 323-334 (Li Na, He Zhengqin, Ye Tailan, et al. Test for Comparison of Array Layout in Natural Source Surface Wave Exploration[J]. Arta Seismologica Sinica, 2015, 37(2): 323-334)
(  0) 0) |
| [12] |
杜亚楠, 徐佩芬, 凌甦群. 土石混合滑坡体微动探测:以衡阳拜殿乡滑坡体为例[J]. 地球物理学报, 2018, 61(4): 1 596-1 604 (Du Yanan, Xu Peifen, Ling Suqun. Microtremor Survey of Soil-Rock Mixture Land Slides:An Example of Baidian Township, Hengyang City[J]. Chinese Journal of Geophysics, 2018, 61(4): 1 596-1 604)
(  0) 0) |
| [13] |
Li J G.Assessing the Applicability of L-Shape Array for Microtremor Survey[D].Tokyo: Japan National Graduate Institute, 2009
(  0) 0) |
| [14] |
Aki K. Space and Time Spectra of Stationary Stochastic Waves, with Special Reference to Microtremors[J]. BullEarthquake Res Inst Tokyo Univ, 1957, 35: 415-456
(  0) 0) |
| [15] |
李传金, 徐佩芬, 凌甦群. 微动勘探法圆形阵列台站数量和分布方式研究[J]. 科学技术与工程, 2016, 16(7): 27-30 (Li Chuanjin, Xu Peifen, Ling Suqun. Study on Station Number and Arrangement of Circle Array in Mircrotremor Survey Method[J]. Science Technology and Engineering, 2016, 16(7): 27-30 DOI:10.3969/j.issn.1671-1815.2016.07.004)
(  0) 0) |
2. Xiamen Vanke Co Ltd, 859 West-Lianqian Road, Xiamen 361000, China
 2020, Vol. 40
2020, Vol. 40


