地球重力场^[1]是地球动力学、固体地球物理学和航空航天学等科学研究与分析的基本场，对国民经济、军事、科研等领域具有十分重要的作用。自上世纪五六十年代采用SLR技术获得低阶次重力场以来^[2]，重力场模型的阶数已从最初的8阶发展至今天EGM08模型的阶和次分别达到2 190和2 159。重力场模型的阶数越来越高，空间分辨率越来越高，从发展来看，实现计算超高阶重力场的需求也越来越大。勒让德函数是地球重力场以及相关领域计算的基础函数，其能否高精度计算至超高阶是重力场解算的关键。目前勒让德函数主要根据其性质进行递推计算，递推算法^[3-5]主要包括列递推法、Belikov递推算法、跨界次递推算法等。在计算时，使用最多的方法为列递推法，但列递推法在球坐标系统下引力及引力梯度会出现奇异因子。虽然于锦海等^[6-7]推导出奇异因子消除公式，但是计算相对复杂；Montenbruck等^[8]在笛卡尔坐标系下，运用列递推算法解决了引力及引力梯度奇异因子问题并且计算方便。由于列递推算法在双精度模式下存在溢出的问题，尤其在1 900阶后某些角度由于误差扩散而无法正确计算。为解决此问题，有些研究者使用尺度因子，例如EGM08模型在计算至2 190阶时，使用尺度因子10²⁵⁰解决向下溢出的问题^[9]；有些使用扩大计算位数的方法^[10-11]。Daras等^[12]利用混合双精度与四精度模式进行计算比较，充分利用星间变率测量结果，通过模拟计算反演得到大地水准面误差为17 nm。本文使用FORTRAN平台，分析比较基于双精度与四精度的重力场解算精度，为超高阶重力场解算等相关研究提供参考。

本文比较了双精度与四精度在计算缔合勒让德函数、数值积分器及反演重力场方面的优缺点。

1 原理

由地球外部无质量这一假设可知，地球引力位在地球外部满足拉普拉斯方程，地球外部空间某点的引力位可以表达成球谐函数，形式如下^[13]：

$ \begin{array}{l} U = \frac{{GM}}{r}{\sum\limits_{n = 0}^\infty {\left( {\frac{R}{r}} \right)} ^n}\sum\limits_{m = 0}^n {({{\overline C }_{nm}}\cos m\lambda + } \\ \;\;\;\;\;\;{\overline S _{nm}}\sin m\lambda ){\overline P _{nm}}\left( {\cos \theta } \right) \end{array} $

(1)

式中，GM为地球万有引力常数，R为地球平均半径，地球外部点(r, θ, λ)分别为地心向径、地心余纬和地心经度。缔合勒让德函数通过式(2)和式(3)的列递推法进行计算：

$ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\overline P _{n, m}} = {f_3}({f_4}{\text{cos}}\theta {\overline P _{n - 1, m}} - {f_5}{\overline P _{n - 2, m}}),\\ m < n - 1 \end{array}\\ \begin{array}{l} {\overline P _{n, n - 1}} = {f_2}{\text{cos}}\theta {\overline P _{n - 1, n - 1}}, \\ m = n - 1 \end{array}\\ \begin{array}{l} {\overline P _{n, n}} = {f_1}\sin \theta {\overline P _{n - 1, n - 1}}, \\ m = n \end{array} \end{array}} \right. $

(2)

其中，

$ \left\{ {\begin{array}{*{20}{c}} {{f_1} = \sqrt {\frac{{2n + 1}}{{2n}}} }\\ {{f_2} = \sqrt {2n + 1} }\\ {{f_3} = \sqrt {\frac{{2n + 1}}{{\left( {n - m} \right)\left( {n + m} \right)}}} }\\ {{f_4} = \sqrt {2n - 1} }\\ {{f_5} = \sqrt {\frac{{\left( {n - m - 1} \right)\left( {n + m - 1} \right)}}{{2n - 3}}} } \end{array}} \right. $

(3)

${\overline C _{nm}}$、${\overline S _{nm}}$为完全正规化后的n阶m次引力位系数，其值通过地面重力或者卫星精密轨道进行反演计算。利用卫星精密轨道解算重力场球谐系数的计算方法主要有动力学积分法、短弧长积分法、能量法等，本文选用动力学积分法。动力学积分法的公式推导思路是基于牛顿运动方程将卫星轨道方程线性化，以此建立卫星精密轨道与球谐位系数的关系式，其微分方程可用式(4)表达，由此推导出动力学积分方法的基本公式(5)^[14]：

$ \left\{ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}\mathit{\boldsymbol{X}}}}{{{\rm{d}}t}} = F(t, \mathit{\boldsymbol{X}})}\\ {\mathit{\boldsymbol{X}}({t_0}) = {\mathit{\boldsymbol{X}}_0}} \end{array}} \right. $

(4)

$ \mathit{\boldsymbol{X}}(t) = {\mathit{\boldsymbol{X}}_{{\rm{ref}}}}(t) + \mathit{\boldsymbol{S}}(t)\delta \mathit{\boldsymbol{p}} + \mathit{\boldsymbol{Q}}(t)\delta \mathit{\boldsymbol{X}}({t_0}) $

(5)

式中，X(t)为卫星精密轨道的位置和速度；X_ref(t)为卫星参考轨道，可利用先验重力场信息等进行数值积分计算获得；S(t)为参数敏感矩阵，是重力场参数等对时间的导数；δp为重力场改正参数及加速度计改正参数等；Q(t)为卫星状态参数对时间的导数；δX(t₀)为初始位置和速度的改正数，上式通过数值积分计算得到观测方程。本文使用的数值计算器为7(8)阶Adam预测校正法及10阶龙格库塔法^[8]。

在式(5)的基础上建立星间变率计算公式：

$ \begin{array}{l} \mathit{\boldsymbol{\dot \rho }}(t) = {{\mathit{\boldsymbol{\dot \rho }}}_0}(t) + {{\mathit{\boldsymbol{\dot Q}}}^{\rm{A}}}\left( t \right)\delta {\mathit{\boldsymbol{X}}^{\rm{A}}}\left( {{t_0}} \right) - \\ {{\mathit{\boldsymbol{\dot Q}}}^{\rm{B}}}\left( t \right)\delta {\mathit{\boldsymbol{X}}^{\rm{B}}}\left( {{t_0}} \right) + \left( {{{\mathit{\boldsymbol{\dot S}}}^{\rm{A}}}\left( t \right) - {{\mathit{\boldsymbol{\dot S}}}^{\rm{B}}}\left( t \right)} \right)\delta \mathit{\boldsymbol{p}} \end{array} $

(6)

式中，$\mathit{\boldsymbol{\dot \rho }}(t)$为GRACE卫星星间变率观测值，${{\mathit{\boldsymbol{\dot \rho }}}_0}(t)$为参考轨道计算得到的参考星间变率，角标A和B为GRACE的两颗卫星的标号。

2 算例 2.1 递推勒让德函数计算精度的比较

勒让德函数是计算地球重力场的基础，勒让德函数计算阶数的精度决定了球谐系数计算的精度。因此本文利用余纬为0.5°~89.5°进行计算，间隔1°。原因在于，缔合勒让德函数${\overline P _n}(cos\theta)$在区间[-90°, 90°]中n-m是偶数时为偶函数，n-m是奇数时为奇函数，所以只需计算[0°, 90°]范围的角度便可。本文分别利用列递推公式(2)在双精度和四精度模式下计算360阶、1 900阶、2 190阶、4 380阶的勒让德函数值。阶误差为：

$ \begin{array}{l} {\varepsilon _n}\left( \theta \right) = \left| {2{{\left[ {{{\overline P }_n}\left( {{\text{cos}} \theta } \right)} \right]}^2} + } \right.\\ \left. {4{{\left[ {\sum\limits_{m = 1}^n {{{\overline P }_{n, m}}} ({\text{cos}})} \right]}^2} - \left( {2n + 1} \right)} \right| \end{array} $

(7)

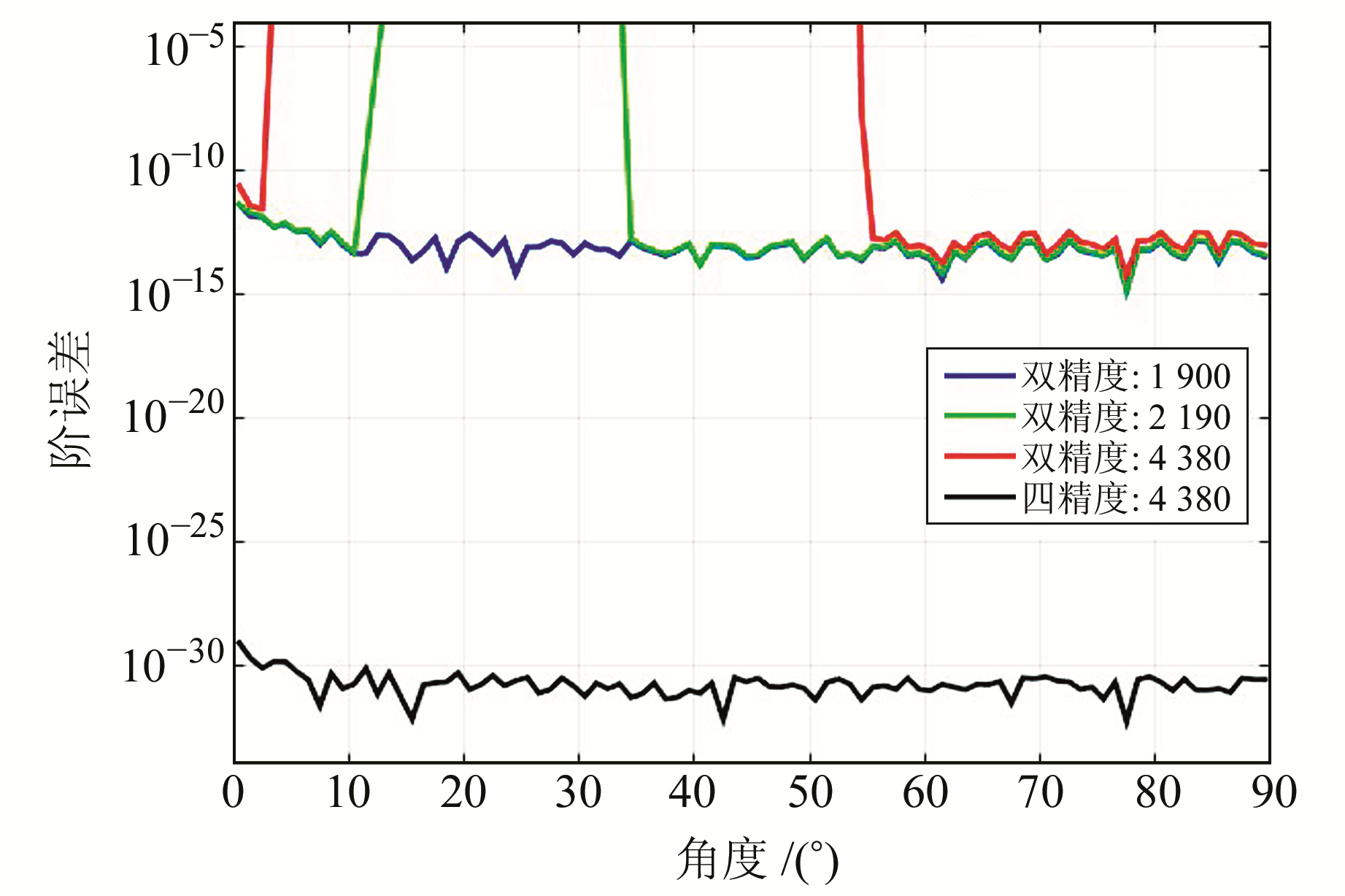
用上式可对每一阶缔合勒让德函数值进行精度评估。其中，ε_n(θ)为角θ第n阶的误差，其值越小表示计算精度越高。由于递推算法对误差具有传递性，因此只需绘制出计算的最后一阶的阶误差便可检验函数的计算精度(图 1)。由图可见，四精度模式下的4 380阶勒让德函数所有角度的计算精度均比双精度模式下的计算精度高10个量级。由于在四精度模式下最大阶4 380不仅满足精度要求并且远大于任何双精度模式的计算精度，因此在四精度模式下不必绘制4 380阶以下其他阶次的阶方误差图。在双精度计算模式下，1 900阶以内所有角度都无发散，且完全满足计算精度要求；当计算至2 190阶时，即EGM08模型的所有阶次，余纬为11.5°~33.5°的范围内不能满足要求；在计算至4 380阶时，余纬为3.5°~54.5°范围内不能满足要求。

由于四精度计算模式需要计算的位数较多，因此其计算量相对双精度会更大。表 1统计了所有角度的勒让德函数在两种模式下的计算时间。由表可知，随着计算阶数的增大，两种精度模式计算的时间都成倍增长。在计算至相同阶次时，四精度模式的计算时间是双精度模式计算时间的40倍左右。因此，若非精度和阶次要求，不建议使用四精度计算模式的程序。当计算至超高阶数时，采用混合计算方式为宜，如计算阶数至2 190阶时，余纬为11.5°~33.5°使用四精度模式计算，而其他角度则在双精度模式下计算。

2.2 数值积分器在两种精度模式下的结果对比

利用动力学方法解算重力场时需要先利用数值积分公式计算出卫星的参考位置和速度，因此有必要对数值积分器的计算精度进行验证。本文使用8阶的Adams-Boshforth法显式公式和Adams-Moulton法隐式公式进行轨道积分计算和变分方程计算，利用8阶的龙格库塔方法进行起步计算。利用已有的初始位置和速度便可求出6个卫星开普勒轨道根数，利用6个轨道根数可求出任意时刻的卫星位置和速度。此种求解方法得到的解析解是无误差的，因此由轨道根数求得的卫星位置和速度可检测数值积分器的积分误差^[8]。

图 2为数值积分器在双精度及四精度模式下的卫星位置及速度的积分误差。由图可见，双精度计算模式的位置和速度的计算误差量级分别为10^-5 m和10^-9 m/s，四精度计算误差比双精度计算误差无论位置或速度都小4个量级。GRACE卫星星间变率测量误差为10^-7 m/s量级，而其位置及速度的误差为cm和亚mm/s量级。因此，双精度计算模式可完全满足精度要求。但由于GRACE Follow-On卫星星间距测量精度提高至50~100 nm，即其误差为10^-8~10^-9 m，因此，双精度计算模式可能无法满足积分误差的需求。而四精度模式下卫星的速度计算量级为10^-14 m/s，完全满足GRACE Follow-On卫星的精度需求。

2.3 不同精度下解算重力场的对比

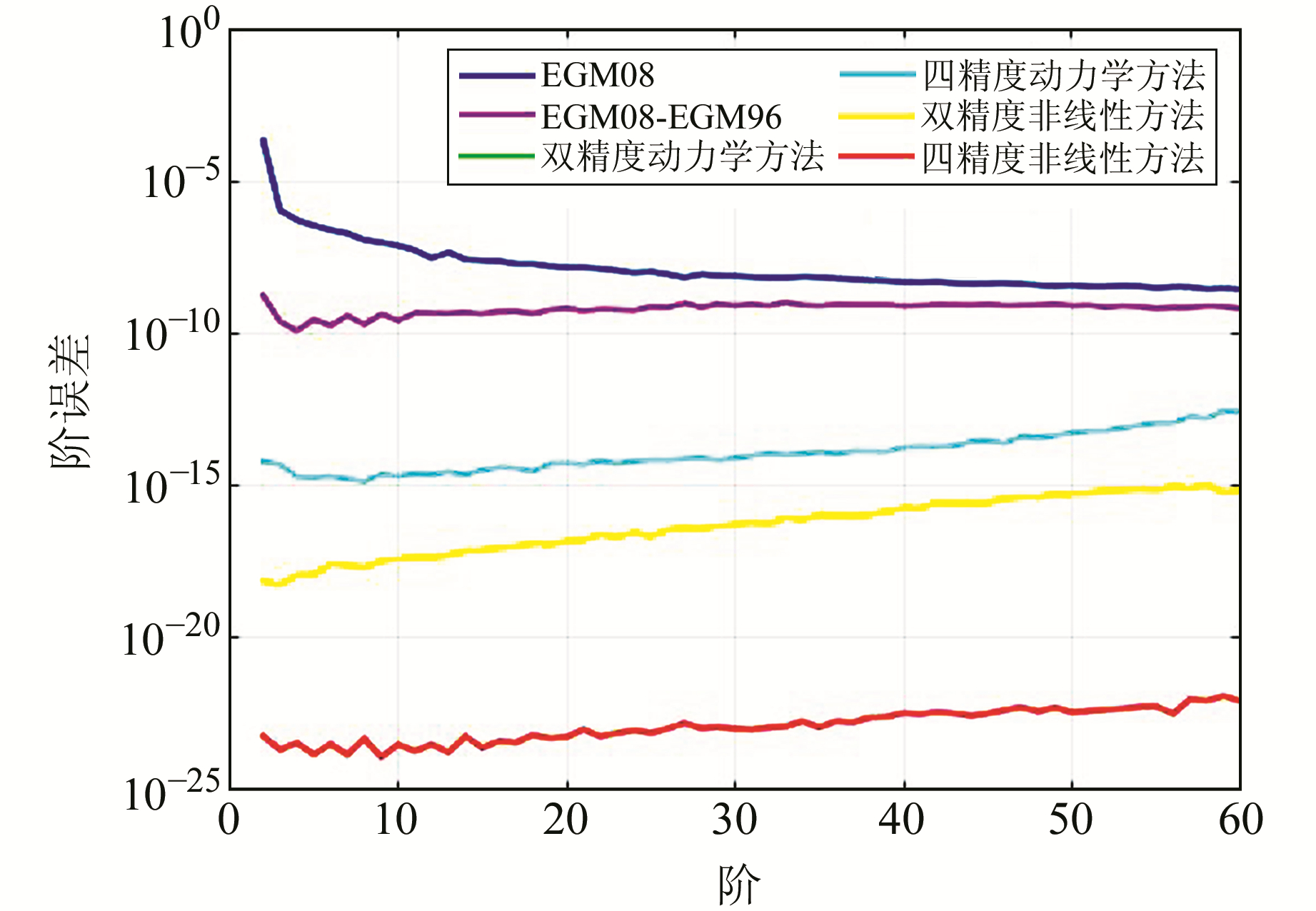
利用动力学积分法和非线性积分方法^[15]在双精度及四精度模式下模拟解算了60阶重力场。模拟参考轨道和真实轨道分别为EGM96和EGM08模型的前60阶重力场，轨道弧长为6 h，计算结果绘制阶误差曲线如图 3所示。由图可见，由于动力学方法使用的是经过线性化处理后的公式，因此其线性化误差相对于数值计算误差为主要误差，其双精度模式与四精度模式计算的阶误差曲线重合。而非线性积分方法的精度比动力学积分方法的精度在双精度模式下高2~3个量级，这主要是由于非线性项的加入提高了计算精度。非线性积分方法在四精度计算模式下比在双精度计算模式下的计算精度提高7个量级左右，这主要是由于数值计算误差减小对其结果的影响。图 4为不同精度下的累积大地水准面误差，动力学方法计算至60阶的累积误差为1.29×10^-5 m，非线性积分方法在双精度及四精度模式下的累积误差分别为8.16×10^-8 m和8.92×10^-15 m。

3 结语

在勒让德函数列递推算法中，四精度模式的计算精度比双精度模式的计算精度高至少1个量级，并且可计算至任意阶数。由于四精度模式的计算用时是双精度模式的40倍左右，因此本文建议双精度与四精度模式混合计算，在双精度模式无法满足精度要求的角度时使用四精度模式计算。

数值积分器7(8)阶Adam预测校正法在双精度计算模式下位置和速度的计算误差量级为10^-5 m和10^-9 m/s，四精度模式相对于双精度模式提高了4个量级。GRACE Follow-On卫星在计算卫星参考轨道及数值积分参数敏感矩阵时，使用四精度计算模式能充分利用其超高的星间变率测量精度，本文建议数值积分器及星间变率建立法方程部分使用四精度计算模式。

将非线性动力学方法在双精度及四精度模式下进行模拟计算，四精度模式的精度比双精度模式的精度提高了7个量级。而动力学方法在两种模式下的计算结果一样，可说明其线性化误差相对于计算误差是主要误差。在计算至60阶累积大地水准面误差时，动力学方法为1.29×10^-5 m，非线性积分方法在双精度及四精度模式下分别为8.16×10^-8 m和8.92×10^-15 m。