2. 云南省地震局形变测量中心,昆明市知春街249号,650041
利用流动重力测量获取构造活动区重力场随时间的非潮汐变化,包括构造活动、质量迁移和密度变化等物理过程,是研究地震孕育、发生和调整过程中的重力场时间和空间变化、提取地震前兆信息、进行地震预报研究的重要途径之一[1-2]。
然而,重力变化异常包含了地下沉积岩的不同岩性和构造、地壳中密度不均匀体及结晶基底起伏变化等因素的混合叠加效应,是一个多源叠加场,包含了浅部和深部场源的非线性、非平稳的综合信息[3]。本文力求从流动重力观测异常获取孕震异常来深入分析研究区域重力变化特征与壳内物质密度变化的关系,而异常的划分成为地震重力数据处理中的关键环节。
小波变换能够将信号分解成不同频率或尺度的成分,其本质是一种窗口可变的傅里叶变换,在空间域和频率域都具有良好的局部分析特性[4-5],因此利用小波多分辨率的特性进行流动重力异常划分,可获得不同深度层次下的异常特征。但很多学者[6-8]利用小波变换对流动重力资料进行的多尺度分析仅停留在对分解异常的定性分析解释上,针对流动重力异常特征如何选择合适的小波基函数和分解阶次并没有相关阐述。
本文通过探讨分析流动重力异常小波多尺度分解效果的影响因素,包括小波基函数、分解阶次和异常特征等,依据异常特征信息,提出选择MATLAB环境下coif5小波基函数、交叉验证确定分解阶次的方法;然后通过模型验证利用该方法进行多尺度分解的有效性;最后对川滇地区201309~201404期差分动态变化异常进行多尺度分解,利用径向对数功率谱对各尺度异常进行定性、半定量分析,并在分解异常中提取到2014年鲁甸MS6.5、景谷MS6.6地震发震前的孕震异常信息,结合地质构造背景对分解异常进行分析解释。
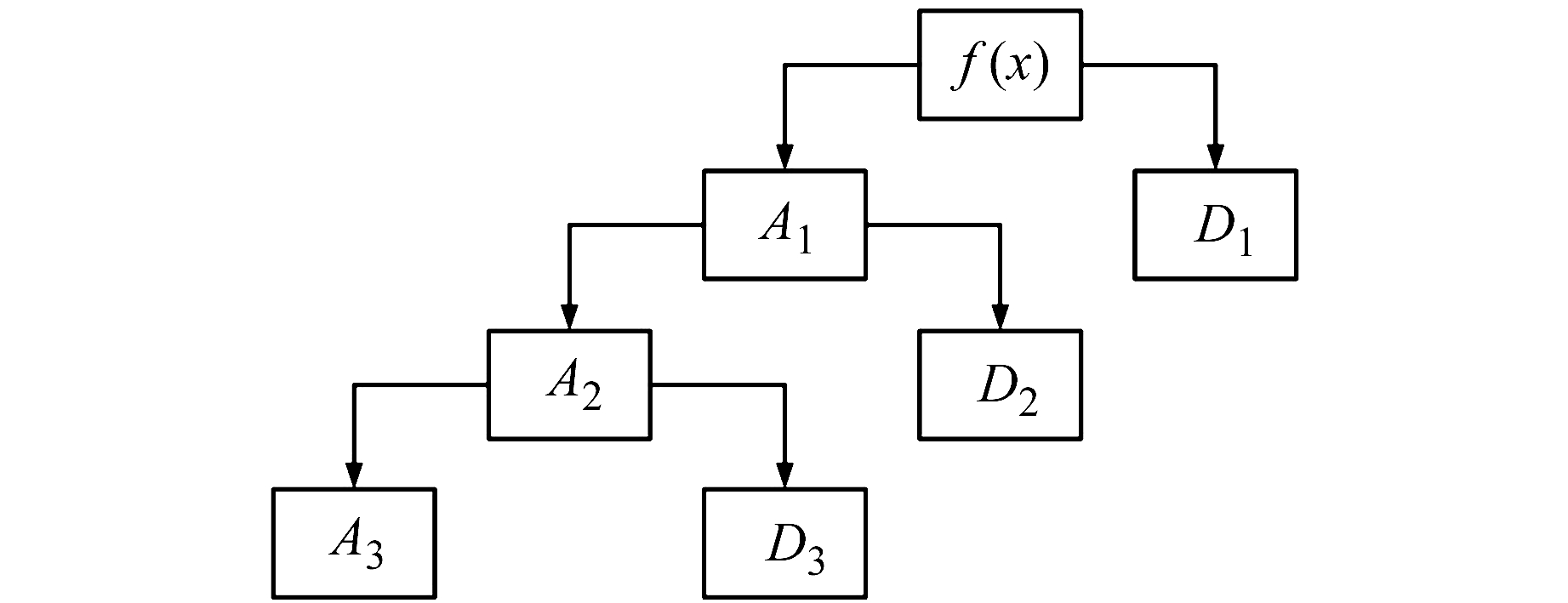
1 小波变换基本理论Mallat等在构造正交小波基时提出多分辨率分析(multi-resolution analysis, MRA)的概念[5],从空间上形象地说明了小波多分辨率的特性。小波多尺度分析通过尺度因子的变化可将信号分解到多层的细节(detail, 简称D)与逼近(approximation, 简称A)上,其中细节D表示高频部分,逼近A表示低频部分。图 1给出3阶尺度分解示意图,对各尺度异常细节和逼近异常进行叠加重构可得到局部异常(D1+D2+D3)和区域异常(A3),实现异常的“二分”。
|
图 1 3阶尺度分解示意图 Fig. 1 The schematic diagram of decomposition by third-order scale |
利用小波变换进行流动重力异常分解时,考虑到模型重力场的变化较为平缓,在选取小波基函数时,趋向选择与异常波形相似且震荡较为平缓、连续和光滑的小波基函数,此外函数还应有较好的对称性、正则性,以及合适大小的支撑长度和消失矩。因此,为了获取较好的分解结果,需综合异常特征、小波特性等因素影响,选取一种合适的小波基函数进行小波变换。
为了提高计算效率并获得较好的分解效果,本文提出一种交叉验证的分解阶次判定方法。假设存在已知异常f (x),设定固定的分解阶次N(N为正整数,一般取6),第i(i≤N)阶异常逼近Ai(趋势变化)与常规“二分法”(如平均场、趋势分析、匹配滤波等)分解得到的区域异常进行对比,若两者异常形态和幅值很接近或者相差很小,则认为i为合理的小波分解阶次;若两者异常形态和幅值差别较大,就用第i-1(i≤N)阶异常逼近Ai-1(趋势变化)进行比对,以此类推,直至两者的异常形态和幅值较为吻合,最终确定小波的分解阶次。该方法不依赖于小波基函数和异常特征,具有易操作、精度高等特点。文中均采用这种方法来确定小波分解阶次,以获得较好的不同尺度下的分解异常。
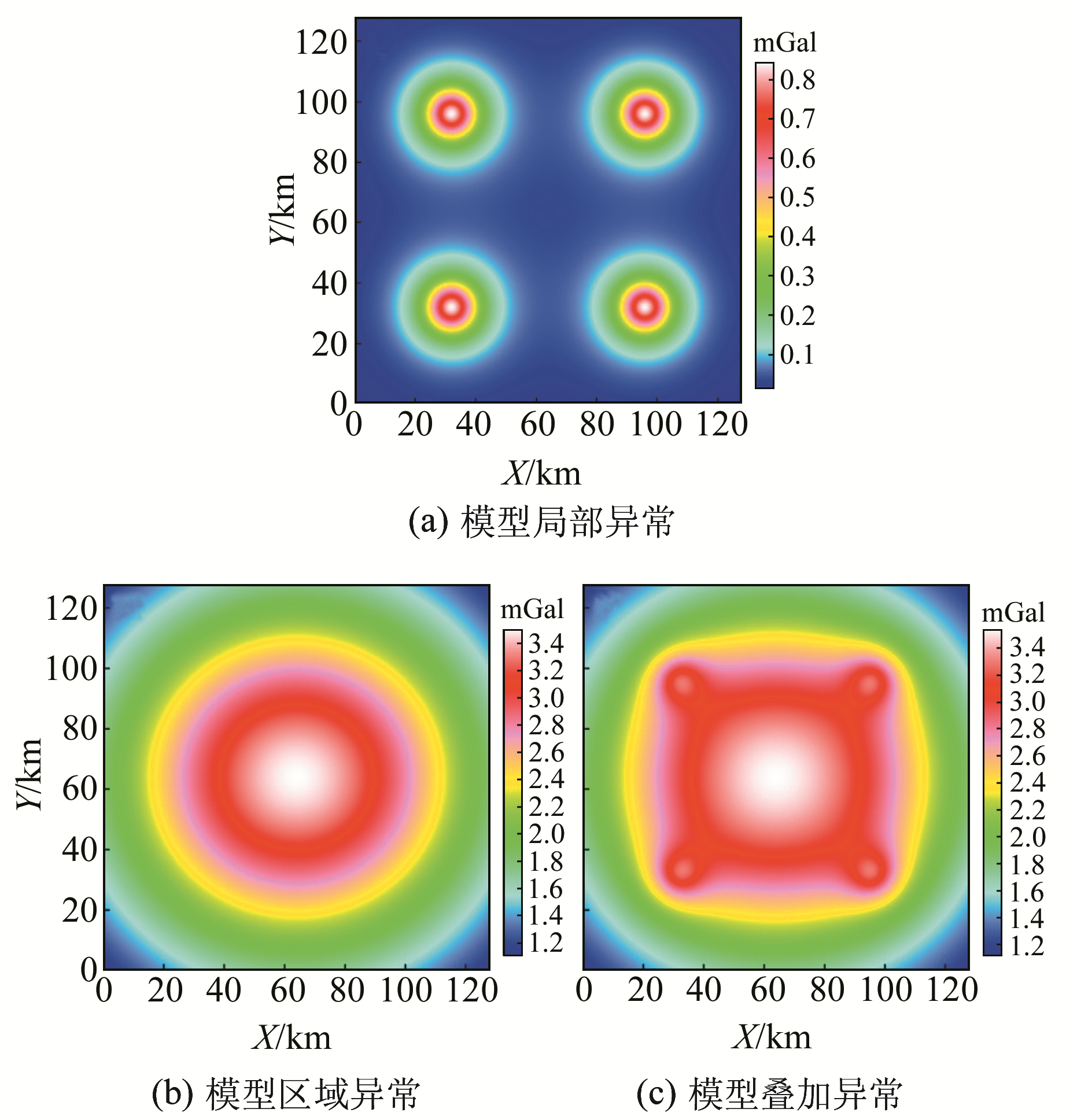
2 模型实验由于野外观测得到的流动重力异常形态变化相对较为平缓,幅值变化不大,为模拟野外观测重力异常,建立模型实验。假设地下存在由4个埋藏较浅、剩余密度较小的球体和1个埋藏较深、剩余密度较大的长方体组成的组合模型块体。长方体的重力异常分布范围广、幅值大,可视为区域异常,4个小球体埋藏较浅,重力异常幅值较小,可视为局部异常,组合模型的相关参数见表 1。将长方体和4个小球体模型组合叠加产生的异常作为叠加异常,组合模型正演重力异常见图 2。
|
|
表 1 组合模型密度参数与几何参数 Tab. 1 The parameters of density and geometric of the combination model |
|
图 2 组合模型重力异常 Fig. 2 The gravity anomalies of combination model |
本文力求从这个多源混合性、非线性和非平稳性位场异常中提取局部异常和区域异常。为获得较好的分解效果和计算效率,选择MATLAB环境下何种小波基函数进行小波变换,需考虑以下两个方面。
1) 小波基函数需有较好的对称性、正则性以及合适大小的支撑长度和消失矩,如Daubechies小波系(dbN,其中N为正整数,下同)具有较好的正则性,其有效支撑长度为2N-1;Symlet小波系(symN)相比于Daubechies小波系具有较好的对称性;Coiflet小波系(coifN)具有更长的支撑长度(6N-1)和更大的消失矩(2N),对称性较好;Biorthogonal小波系(biorNr.Nd)利用不同类型的小波进行分解和重构,因此其分解和重构函数的支撑长度、正则性和消失矩还是存在一定程度的差异;Mexican Hat小波和Morlet小波不存在尺度函数,因此其不具有正交性;Meyer小波不具有紧支撑性,所以此类小波不能进行离散小波变换。
2) 选择与异常波形相似、连续和光滑的小波,如Haar(db1)小波在支撑区域内是单个矩形波,且不连续;db2~db3、sym2~sym4、coif1~coif2、bior1.1、bior2.2、bior3.3、bior4.4、bior5.5等小波函数波形震荡变换较为剧烈,与平缓的模型异常波形不相符。
此外,李健等[9]考虑到小波变换的本质和小波基函数性质,并结合信号的特性,通过模型实验和实际数据得出,利用双正交bior3.5进行一维小波变换能够获得较好的分解效果,然而其对二维信号的分析没有作相关阐述。一些学者[6-8]根据此结论,也主张运用双正交小波bior3.5直接对实际二维重力异常进行多尺度分解,然而在对各尺度异常进行分析解释时,上述研究均缺少模型实验以验证该小波实现重力异常分离的有效性。
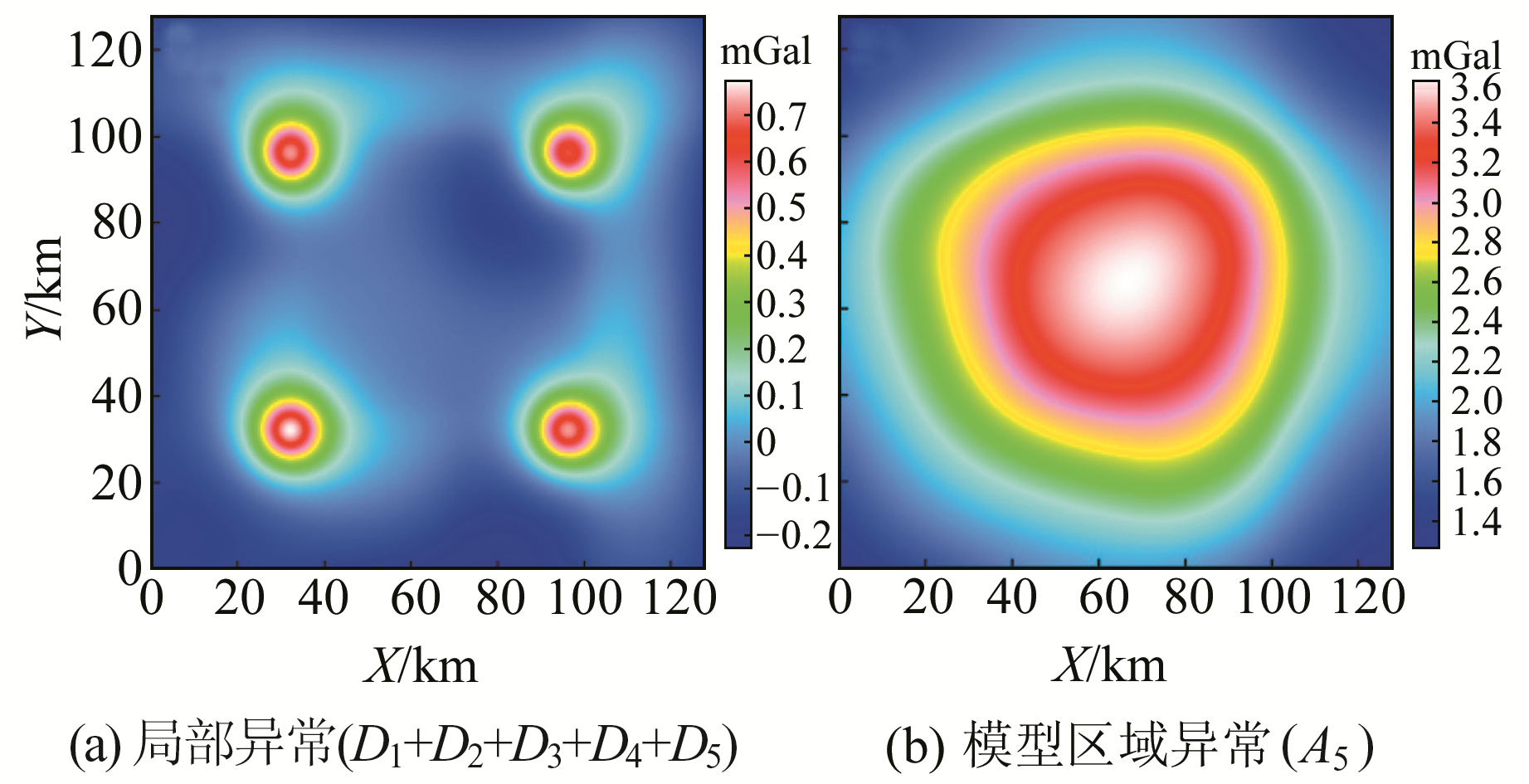
因此,本文尝试利用双正交小波bior3.5对组合模型异常进行多尺度分解。首先利用交叉验证方法确定分解阶次为5阶;然后将1~5阶细节累加重构结果作为局部场(D1+D2+D3+D4+D5),5阶逼近作为区域场(A5),实现异常的“二分”(图 3)。由于双正交小波bior3.5中分解和重构小波基函数与异常波形存在一定差异,分解重构局部和区域异常形态均存在一定程度的畸变失真,并且异常幅值大小与理论值存在一定差距。
|
图 3 bior3.5小波5阶分解重构异常 Fig. 3 The reconstruction anomalies of fifth-order decomposition by bior3.5 wavelet |
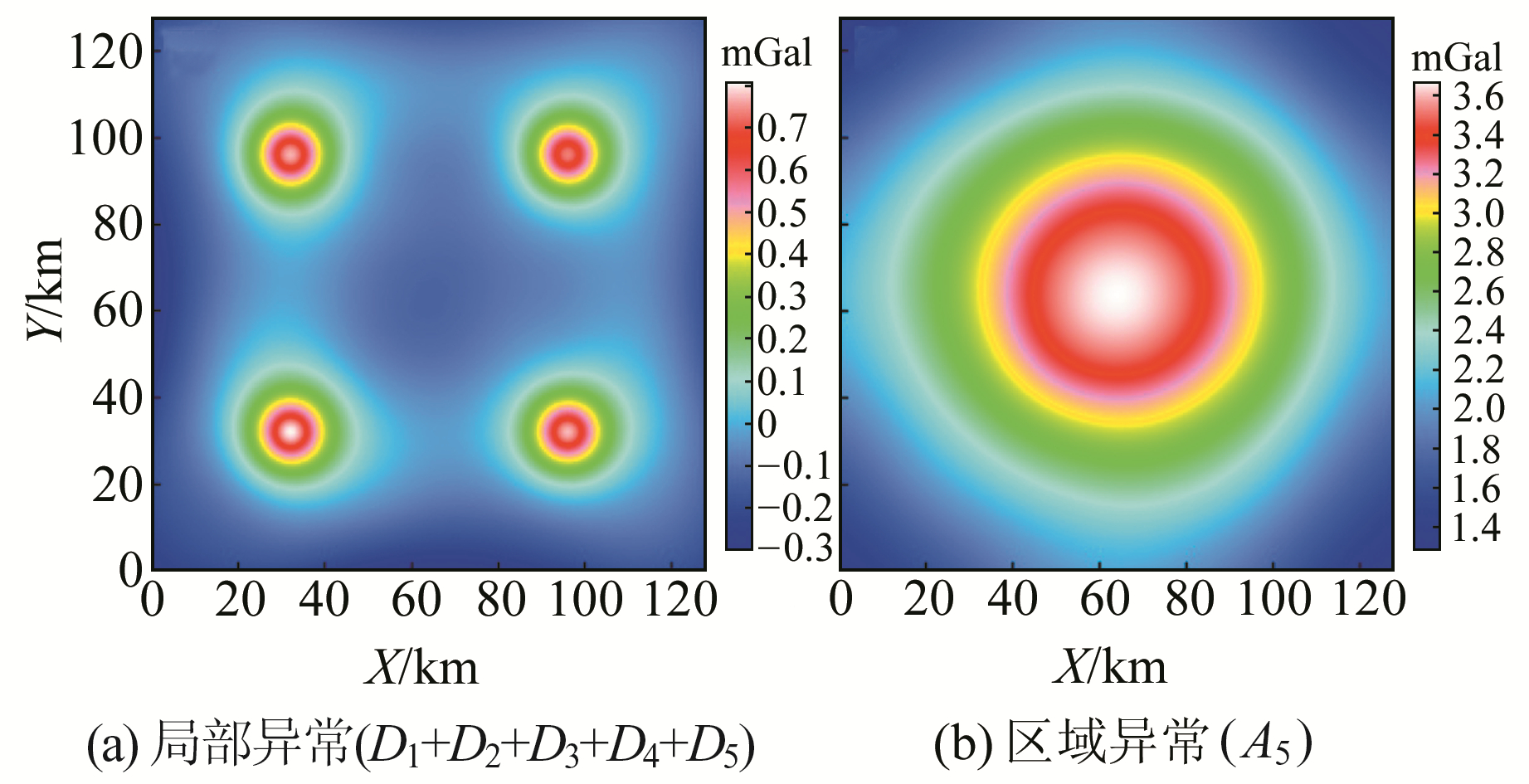
另外,综合考虑小波基函数性质和异常形态特征,选取Coiflet小波系中对称性较好的coif5小波基函数,其支撑长度为29,消失矩为10,且与异常形态相近似。同样,利用coif5小波基函数对组合模型异常进行5阶多尺度分解,其重构异常见图 4。可以看出,coif5小波分解得到的局部和区域异常中的4个球体和长方体的异常形态和幅值与模型理论异常均具有较好的一致性。通过对比bior3.5和coif5小波分解异常发现,coif5小波能够获得较好的分解效果。因此可以定性地认为,coif5小波能够将组合模型异常中的局部异常和区域异常有效分离出来,获得较为理想的分离效果。另外,由于组合模型异常较为简单,对分解各尺度异常不进行过多解释。
|
图 4 coif5小波5阶分解重构异常 Fig. 4 The reconstruction anomalies of fifth-order decomposition by coif5 wavelet |
利用径向对数功率谱方法[10-11]对coif5小波分解得到的局部异常和区域异常进行场源似深度估计(见图 5,其中红色虚线为拟合直线)。由图 5(a)可见,组合模型异常功率谱曲线可以较好地拟合出两条直线,即异常中存在两种不同埋深的场源。图 5(b)所示局部异常的功率谱曲线可以拟合出一条直线,利用该直线斜率估算的场源似深度h估≈ 9.6 km,这与球体模型理论中心埋深h理= 10 km一致。同样,图 4(c)所示的区域异常对应的场源似深度H估≈ 79.62 km,该场源深度估算值与模型长方体中心埋深H理= 80 km吻合。此外,通过计算发现,图 5(b)和5(c)中拟合的直线与图 5(a)中拟合的2条直线存在一一对应关系。因此,借助径向对数功率谱方法对coif5小波分解得到的局部异常和区域异常进行场源似深度估计,可以看出,coif5小波分解异常是具有实际地质含义的,其主要体现在异常所对应的场源深度上,半定量地解释了coif5小波能够有效地将局部异常和区域异常从组合模型异常中分离出来。

|
图 5 coif5小波分解异常的径向对数功率谱曲线 Fig. 5 The radial logarithmic power spectrum curves of the composition anomalies by coif5 wavelet |
综上可知,利用coif5小波分解得到的局部异常和区域异常不仅在异常形态和幅值上,而且在分解异常所对应的场源埋深上与理论情况均能够较好地吻合,可以较好地揭示场源赋存的地质信息,定性、半定量地揭示小波变换用于重力异常分解的有效性。
3 实际应用川滇地区位于青藏高原东南部,地貌起伏较大,地形地势复杂,山谷和河流纵横交错。从构造方面来看,该区主要分布在滇南活动地块南段、川滇菱形块体南段和长江中下游断块构造亚区西部。由于川滇地区位于欧亚板块与印度洋板块中国大陆碰撞带东缘、造山运动的突出位置,地质及其相关的地球物理背景比较复杂,断裂构造纵横交错。由于该区特殊的地理位置,使其成为中国大陆地壳构造运动最为强烈、地震活动频率最高且强度最大的区域之一。近年来,该区域受到国内学者[12-13]的密切关注,复杂的构造环境与强烈而频繁的地震活动成为该区域的研究热点。
本文收集了2013~2014年川滇地区流动重力区域数据资料,测点与测网分布基本上覆盖全区(见图 6, 其中红色五角星为鲁甸MS6.5地震主震位置;蓝色五角星为景谷MS6.6地震主震位置)。为了提取鲁甸MS6.5、景谷MS6.6地震发震前的孕震异常,以两次地震发震前最近的201309~201404期重力差分动态变化数据(图 7)为例进行分析。采用小波变换进行多尺度分解实现位场的分离,然后分析不同尺度意义下的重力场变化特征,并综合测区断裂构造的强震危险性进行讨论。

|
图 6 川滇地区流动重力测网及构造线 Fig. 6 The mobile gravity network and structural line by Sichuan-Yunnan region |
|
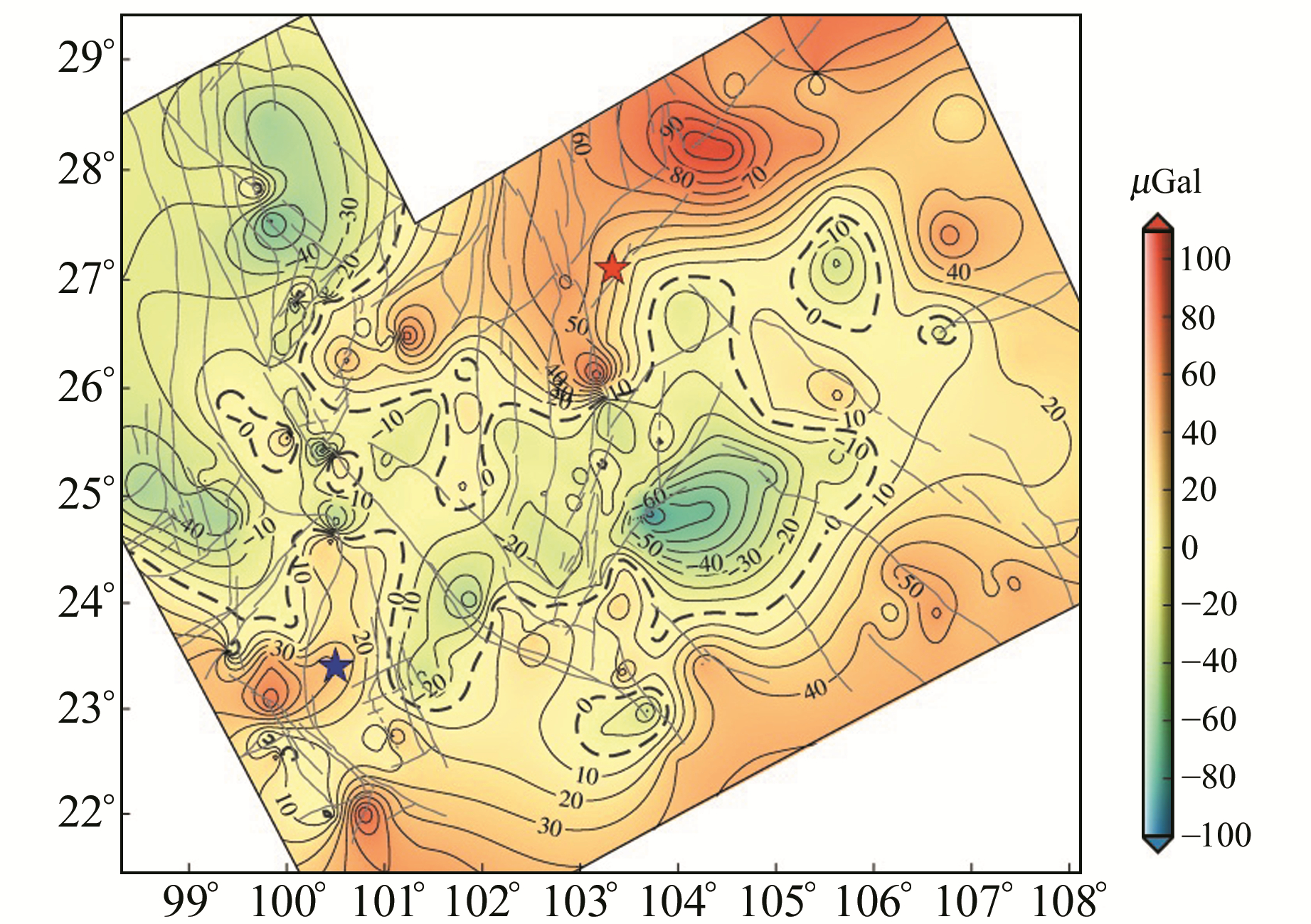
图 7 201309~201404期重力差分动态变化 Fig. 7 The differential dynamic gravity changes in the period of 201309-201404 |
图 7显示,测区以香格里拉、大理、楚雄、罗平、兴义、六盘水、毕节等地为中心表现为显著的负异常区域,周围为大范围的正异常,正负异常之间形成重力变化高梯度带和零值线,零值线的位置和走向发生一定程度的转变弯曲,呈现中间低、四周高的整体变化特征。鲁甸地震震中位于正异常区域,靠近正负异常变化高梯度带位置;景谷地震震中位于正异常边缘,异常变化特征不明显。两次地震主震位置处的异常是地下不同场源、不同埋深和不同地质体的叠加响应,因此,单纯分析201309~201404期重力差分动态变化的局部异常特征不能准确、有效地提供测区重点区域强震危险性和地震趋势的判定意见。
利用小波变换对该期数据进行多尺度分解,从不同尺度的异常中获取与孕震相关的异常信息。选用coif5小波基函数进行位场的分离,利用交叉验证方法确定的分解阶次为6阶,因此,利用小波变换对上述异常进行6阶多尺度分解,获得不同波长的变化异常(图 8)。图中,D1、D2、D3异常为较高频率零星异常,其反映了近地表或浅部地下岩体、地质构造的变化信息,这里不作太多解释;D4异常中,鲁甸地震震中位置存在串珠状异常,幅值差异变化达60 μGal,景谷地震震中位置存在正负异常梯度带,幅值差异变化约为80 μGal;D5异常中,景谷地震震中位置两侧存在幅值变化的正负异常,其位于正负变化高梯度带和零值线附近,鲁甸地震震中位于零值线上;D6异常中,同样地,鲁甸地震震中位于正负异常变化的高梯度带上,异常幅值差异变化达60 μGal,景谷地震震中位于零值线附近,两者并不重合,且其周边存在较为明显的“四象限”异常;A6异常中,鲁甸和景谷地震都位于重力变化梯度带上,而鲁甸地震震中位置异常的幅值差异变化相对较为剧烈。

|
图 8 201309~201404期重力差分动态变化coif5小波多尺度分解结果 Fig. 8 The multi-scale decomposition results of differential dynamic gravity changes in the period of 201309-201404 by coif5 wavelet |
综上所述,D4~D6细节和A6区域异常显示,2次强震发震位置均具有判断发震危险性的重力变化特征(零值线、重力值变化高梯度带、“四象限”异常),上述不同尺度异常特征对两次地震发震均有反映,小波多尺度分解获得了多分辨率的异常信息,这比单纯地分析和解释201309~201404期单一差分异常更具说服力。
利用对数功率谱曲线计算上述小波分解的D4~D6细节异常所对应的不同深度层次上的场源深度,其场源估计深度分别为48.4 km、77 km、127.2 km。可以看出,随着分解尺度的增加,异常波长及其反映的场源似深度逐渐增大,分解的各尺度异常被赋予了实际的地质含义。
场源似深度较深的D4~D6异常能够反映出鲁甸MS6.5和景谷MS6.6地震的孕震异常,然而这两次地震的震源深度仅分别约为12 km、5 km。这是由于,场源似深度是利用地下不同规模、不同形态和不同埋深的不均匀地质体的综合响应异常来估算的,并不是一个真实存在的场源深度,它用来表征各场源的平均深度,而实际上地下场源埋深有大于平均深度的,也有小于平均深度的,发震位置和场源构造变形位置并不是一个严格意义上的统一体。针对这两次地震的发震机理,笔者认为,可能由于较深层次上的场源构造运动带动较浅深度(中上地壳)的构造体运移,产生一系列复杂应力,逐渐变形破裂,导致地震震中位置存在于质量运移的过渡区域,即重力变化梯度带及其周边位置处,这与石磊等[12]通过重力三维反演结果认为鲁甸地震震中位置对应于地表水平重力变化高梯度带及梯度带转换部位的判断相吻合。
此外,将前6阶细节异常进行组合叠加得到的异常(D1+D2+D3+D4+D5+D6)作为局部异常,第6阶逼近异常(A6)作为区域异常,实现了异常“二分”(图 9)。由图可见,鲁甸MS6.5地震位于正负异常变化高梯度带上,景谷MS6.6地震位于“四象限”异常附近。此“二分”法分解得到的异常与原始异常相比,其分布范围及特征较为明显,分析和解释相关孕震异常更具有说服力。

|
图 9 201309~201404期重力差分动态变化coif5小波分解重构结果 Fig. 9 The reconstruction of decomposition results of differential dynamic gravity changes in the period of 201309-201404 by coif5 wavelet |
综上可知,利用小波变换对201309~201404期重力异常进行多尺度分解来获取不同尺度下的孕震异常是有效的;借助功率谱曲线估算不同尺度下的场源深度,提取到鲁甸MS6.5和景谷MS6.6地震发震前的孕震异常,包括正负异常高梯度带、零值线、“四象限”异常等,进而对孕震异常进行定性、半定量解释。说明小波变换能有效提取两次强震的孕震异常特征,小波多尺度分析方法可对重点危险区的紧迫性和震后趋势研判提供一种思路。
4 结语本文提出选择coif5小波基函数、交叉验证确定分解阶次的新方法用于流动重力异常的小波多尺度分解。经过模型实验和实例验证,该方法能有效分离不同深度的场源异常,且分解得到的各尺度异常具有实际地质含义。
利用小波变换多分辨率的特性提取川滇地区流动重力异常特征,获得以下结论与认识:
1) 利用coif5小波基函数、交叉验证方法确定分解阶次进行小波多尺度分解,不仅能够最大限度地保持异常特征,而且异常能够保幅,可以结合径向对数功率谱方法,定性、半定量地揭示小波变换用于流动重力异常分解的有效性。
2) 用小波变换对201309~201404期资料分解得到的D4~D6异常、重构的局部和区域异常中,鲁甸MS6.5和景谷MS6.6发震前均存在明显的孕震异常特征。在判定测区地震危险性和地震趋势变化方面,综合利用小波分解的各尺度异常,比单纯地分析解释单一差分动态变化异常更具有说服力。
| [1] |
祝意青, 闻学泽, 孙和平, 等. 2013年四川芦山MS7.0地震前的重力变化[J]. 地球物理学报, 2013, 56(6): 1 887-1 894 (Zhu Yiqing, Wen Xueze, Sun Heping, et al. Gravity Changes before the Lushan, Sichuan, MS=7.0 Earthquake of 2013[J]. Chinese Journal of Geophysics, 2013, 56(6): 1 887-1 894)
(  0) 0) |
| [2] |
王同庆, 陈石, 梁伟锋, 等. 2016年门源MS6.4地震前的区域重力场变化与定量参数分析[J]. 地震地质, 2018, 40(2): 349-360 (Wang Tongqing, Chen Shi, Liang Weifeng, et al. Variations of the Gravity Field and Quantitative Parmeter Analysis before the 2016 Menyuan MS6.4 Earthquake[J]. Seismology and Geology, 2018, 40(2): 349-360 DOI:10.3969/j.issn.0253-4967.2018.02.005)
(  0) 0) |
| [3] |
张双喜, 陈超, 王林松, 等. 二维经验模态分解及其在位场去噪和分离中的应用[J]. 地球物理学进展, 2015, 30(6): 2 855-2 862 (Zhang Shuangxi, Chen Chao, Wang Linsong, et al. The Bidimensional Empirical Mode Decomposition and Its Applications to Denoising and Separation of Potential Field[J]. Progress in Geophysics, 2015, 30(6): 2 855-2 862)
(  0) 0) |
| [4] |
Grossmann A, Morlet J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape[J]. SIAM Journal on Mathematical Analysis, 1984, 15(4): 723-736 DOI:10.1137/0515056
(  0) 0) |
| [5] |
Mallat S G. A Theory for Multi-Resolution Signal Decomposition: The Wavelet Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693 DOI:10.1109/34.192463
(  0) 0) |
| [6] |
刘芳, 祝意青, 陈石. 华北时变重力场离散小波多尺度分解[J]. 中国地震, 2013, 29(1): 124-131 (Liu Fang, Zhu Yiqing, Chen Shi. Multi-Scale Decomposition of Wavelet of the Temporal Gravity Variation in North China[J]. Earthquake Research in China, 2013, 29(1): 124-131 DOI:10.3969/j.issn.1001-4683.2013.01.014)
(  0) 0) |
| [7] |
李大虎, 丁志峰, 梁明剑, 等. 四川地区流动重力资料的位场分离与异常特征提取[J]. 地震学报, 2014, 36(2): 261-274 (Li Dahu, Ding Zhifeng, Liang Mingjian, et al. Field Separation and Anomaly Feature Extration of Mobile Gravity Data in Sichuan Area[J]. Acta Seismologica Sinica, 2014, 36(2): 261-274 DOI:10.3969/j.issn.0253-3782.2014.02.011)
(  0) 0) |
| [8] |
郭树松, 刘芳, 祝意青. 小波多尺度分解在地震预测中的应用[J]. 大地测量与地球动力学, 2014, 34(4): 34-38 (Guo Shusong, Liu Fang, Zhu Yiqing. On Earthquakes Predicting by Using Multi-Scale Decomposition Technique[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 34-38)
(  0) 0) |
| [9] |
李健, 周云轩, 许惠平, 等. 重力场数据处理中小波母函数的选择[J]. 物探与化探, 2001, 25(6): 410-417 (Li Jian, Zhou Yunxuan, Xu Huiping, et al. The Selection of Wavelet Generating Functions in Data Processing of Gravity Field[J]. Geophysical & Geochemical Exploration, 2001, 25(6): 410-417 DOI:10.3969/j.issn.1000-8918.2001.06.002)
(  0) 0) |
| [10] |
Spector A, Grant F S. Statistical Model for Interpreting Aeromagnetic Data[J]. Geophysics, 1970, 35(2): 293-302 DOI:10.1190/1.1440092
(  0) 0) |
| [11] |
张双喜, 陈兆辉, 王同庆, 等. 利用二维模态分解提取川滇地区流动重力异常特征[J]. 大地测量与地球动力学, 2018, 38(4): 407-413 (Zhang Shuangxi, Chen Zhaohui, Wang Tongqing, et al. The Extraction of Abnormal Feature of Mobile Gravity in the Sichuan-Yunnan Region Using BEMD Method[J]. Journal of Geodesy and Geodynamics, 2018, 38(4): 407-413)
(  0) 0) |
| [12] |
石磊, 贾晓东, 陈石, 等. 2014年云南鲁甸6.5级地震前重力变化特征与3维反演[J]. 地震地质, 2014, 36(4): 1 217-1 227 (Shi Lei, Jia Xiaodong, Chen Shi, et al. Gravity Changes before the Ludian, Yunan, MS6.5 Earthquake of 2014 and the Three-Dimensional Inversion Research[J]. Seismology and Geology, 2014, 36(4): 1 217-1 227)
(  0) 0) |
| [13] |
孟庆筱, 党学会. GPS约束下九寨沟地区断裂带现今运动速率的非连续接触模拟研究[J]. 地震研究, 2018, 41(3): 390-397 (Meng Qingxiao, Dang Xuehui. Research on Current Crustal Deformation in the Jiuzhaigou Area under the Constraints of GPS Results by Discontinuous Contact Model[J]. Journal of Seismological Research, 2018, 41(3): 390-397 DOI:10.3969/j.issn.1000-0666.2018.03.007)
(  0) 0) |
2. Deformation Survey Center of Yunnan Earthquake Agency, 249 Zhichun Street, Kunming 650041, China
 2020, Vol. 40
2020, Vol. 40

