2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
土壤湿度在水文、气象和农业环境研究中具有重要作用,它在环境科学等领域可以作为衡量水资源循环的标准[1]。对于土壤湿度的长期监测来说,传统方法存在成本高、处理操作复杂、适用范围有限等缺点[2]。近年来,利用GPS反射信号反演土壤湿度成为新型的监测方法,它具有精度高、连续性强、适用范围广等优点,广泛应用于海平面、雪深、土壤湿度监测等方面[3]。Larson等[4]于2008年首次提出GPS-IR土壤湿度反演技术,结果表明,GPS信噪比振幅与土壤湿度波动密切相关;Larson[5]进一步指出,多路径信号适用于水平1 000 m2、垂直1~6 cm范围地表土壤湿度监测;Bilich等[6]较早对卫星直射、反射信号的分离进行研究,利用小波变换实现了反射信号相关信息的分离,并证实反射信号的幅度和频率与多路径环境有着密切的关系;Chew等[7]从GPS信噪比观测值中获取相对延迟相位、振幅和有效反射高等3个参数,进一步证实相位、振幅与土壤湿度变化的关系,并建立相对延迟相位对土壤湿度的线性回归模型,在单一裸土环境下,相对延迟相位是土壤湿度反演的最优参数;敖思敏等[8]通过实验表明,利用GPS信噪比(signal-to-noise ratio,SNR)观测值中的多路径反射分量能够反映土壤湿度变化的趋势, 建立指数函数回归模型,可以很好地描述相对延迟相位与土壤湿度之间的关系;Wang等[9]研究表明,利用GPS-IR技术反演潮位变化时,应用离散小波分解能有效降低SNR数据中的噪声,相比较长SNR数据序列,采用小波分解,在较短SNR数据序列消噪后通过Lomb-Scargle谱分析方法估计多路径频率的性能更佳;针对土壤湿度估算模型的研究,任超等[10]引入最小二乘支持向量机,建立相对延迟相位与土壤湿度的非线性回归模型,实现了较高的反演精度。已有研究表明,卫星反射信号分离对于土壤湿度的反演非常重要,分离的好坏直接影响到反演精度。已有的研究往往采用低阶多项式拟合进行分离,但该方法可能存在局部拟合精度较低的问题。SNR中的卫星直射信号往往呈现趋势性变化,如果能够通过某种方法或手段准确地提取卫星直射信号,将会提高分离卫星反射信号的精度。考虑到小波分析在时域和频域同时具有良好的局部化性质,并已广泛应用于图像去噪、信号趋势识别等领域[11],本文基于小波分析原理建立卫星反射信号分离模型。
1 原理与方法 1.1 卫星信号反射原理GPS-IR的核心观测值就是SNR,它是反映接收机天线信号质量的指标[12]。SNR表达式为:
| $ \text{SNR}={{\mathit{S}}_{\text{d}}}\left( 0 \right)+{{\mathit{S}}_{\text{m}}}\left( \varphi \right)\ $ | (1) |
式中,SNR表示信噪比观测值;Sd(0)表示直射信号,“0”代表初始相位;Sm(φ)表示反射信号,φ代表反射信号的相位值。因此,GPS接收机接收的信号往往是卫星直接、反射信号叠加的混合信号(图 1)。
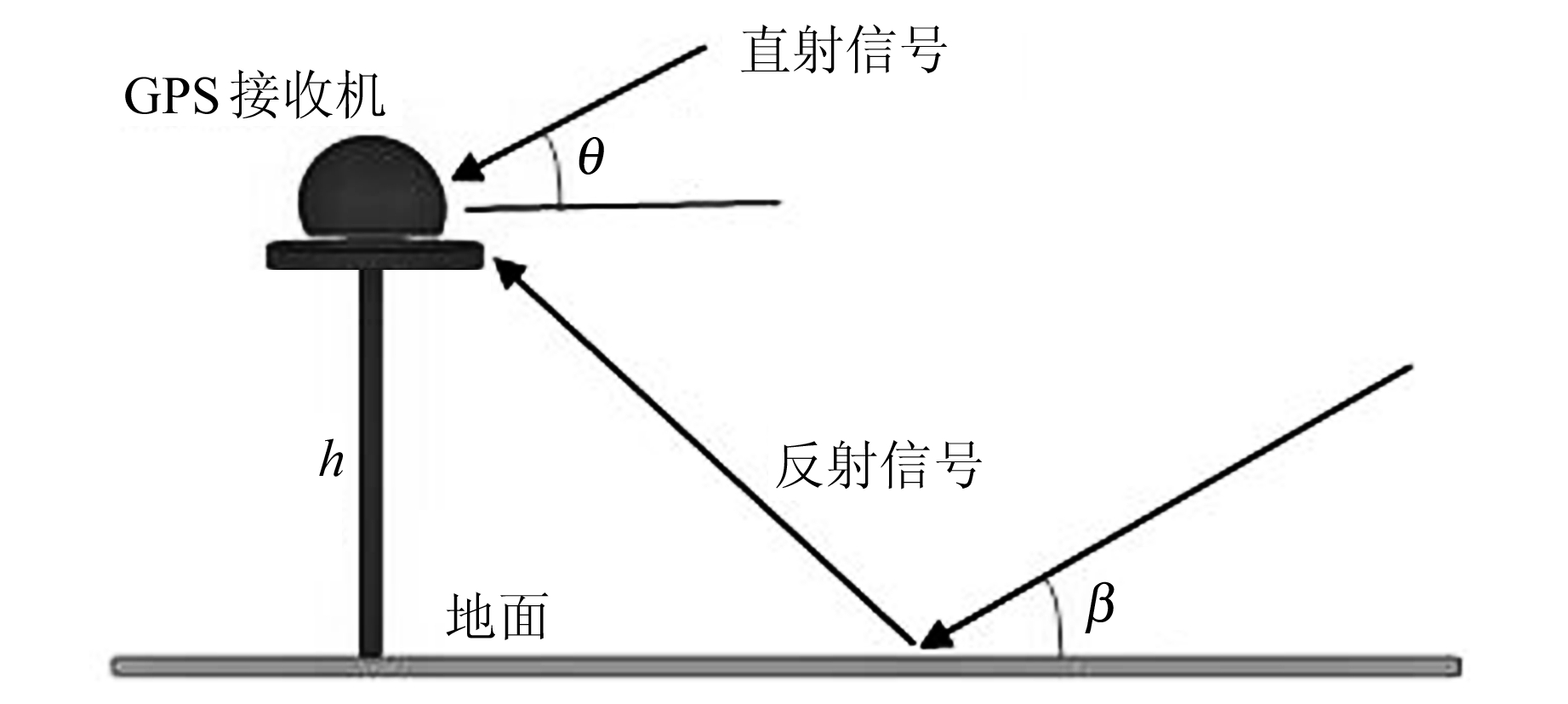
|
图 1 地面多路径误差几何模型 Fig. 1 Ground multipath error geometry model |
图 1中,θ代表卫星信号入射高度角;h代表天线距离底面的垂直高度;β代表卫星信号入射与地面间反射的夹角,一般情况下反射信号的入射高度角为β。
结合图 1可推出,卫星直射、反射信号之间的相位差ψ与入射角θ相关。随着时间t的变化,ψ也会发生变化,其变化频率为:
| $ \frac{\text{d}\psi }{\text{d}t}=\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }2h~\frac{\text{d}(\text{sin}\theta )}{\text{d}t} $ | (2) |
从式(2)可见,ψ与sinθ之间存在线性关系。Chew等[7]研究发现,卫星反射信号与高度角存在正弦(或余弦)关系[8]:
| $ \text{SN}{{\text{R}}_{\text{m}}}={{A}_{\text{m}}}\text{cos}\left( \text{ }\!\!~\!\!\text{ }\frac{4\text{ }\!\!\pi\!\!\text{ }h}{\lambda }\text{sin}\theta +\varphi \right) $ | (3) |
式中,SNRm表示反射信号的信噪比分量,Am表示反射信号的多路径干涉幅度,h表示接收机天线高,θ表示卫星高度角,φ表示反射信号的相对延迟相位。
可见,利用GPS-IR反演土壤湿度的关键是卫星反射信号的有效分离。本文以分离卫星反射信号为研究对象,引入小波分析原理构建分离模型,以提高分离反射信号的精度。
1.2 卫星反射信号分离原理设SNR观测值f(t)为:
| $ \begin{align} & f\left( t \right)=\left[ x_{1}^{0}x_{2}^{0},\ldots ,x_{t}^{0} \right],~ \\ & \ \ \ \ \ t=1,2,3,\ldots ,I \\ \end{align}\ $ | (4) |
式中,t为历元;在利用小波原理分离卫星反射信号的应用中,f(t)为原始信号。小波分析识别信号发展趋势的问题可等价为:将f(t)通过小波滤波器H、G分解成多组不同特征的时间序列,其中一组信号能够反映时间序列内变化趋势的低频部分,其余为随机扰动的高频部分。分解算法为[13-14]:
| $ {{A}_{j}}\left[ f\left( t \right) \right]=\sum\limits_{k}{H\left( 2t-k \right){{A}_{j-1}}\left[ f\left( t \right) \right]} $ | (5) |
| $ {{D}_{j}}\left[ f\left( t \right) \right]=\sum\limits_{k}{G\left( 2t-k \right){{A}_{j-1}}\left[ f\left( t \right) \right]} $ | (6) |
式中,Aj为低频部分小波系数,j为分解层数,Dj为高频部分小波系数,f(t)为原始信号,t为时间序列号。
经式(5)和式(6)分解后,通过重构算法得到重构后的低频信号:
| $ \begin{align} & v{{A}_{j}}=2\left\{ \sum\limits_{k}{h\left( 2t-k \right){{A}_{j+1}}\left[ f\left( t \right) \right]+} \right. \\ & \ \ \ \ \ \ \left. \sum\limits_{k}{g\left( t-2k \right){{D}_{j+1}}\left[ f\left( t \right) \right]} \right\} \\ \end{align} $ | (7) |
式中,h和g为重构小波滤波器,Aj为重构得到的低频信号。
2 实验分析本文选取来自于美国板块边界观测计划(plat boundary observatary,PBO)的P041测站的监测数据进行实验,GPS监测数据可从网站http://www.unavco.org/获得;土壤湿度参考值来自网站http://xenon.col-orado.edu/portal,每天的土壤湿度参考值是基于该测站不少于8个卫星轨道的L2C载波反演的平均值来实现的。该测站位于105.194 267°W、39.949 493°N,能够记录L2观测值。从图 2可以看出,测站周围视野开阔,且地形平坦、植被稀疏,利于土壤湿度的监测。同时,该测站采用钢制三脚架安置,接收机型号为TRIMBLE NERT9,采用SCIT天线罩,天线型号为TRM59800.80,可以长期监测高质量的SNR观测值,并很早就开展土壤湿度的反演研究,具有一定的代表性。

|
图 2 P041测站 Fig. 2 P041 station |
本实验采用P041测站2012年第98~173天(共76 d)的数据进行分析,采样率为30 Hz。为了验证本文方法的可行性,设置两种方案进行对比分析:方案1,基于二阶多项式拟合的卫星反射信号分离方法;方案2,基于小波db4的卫星反射信号分离方法。首先,采用TEQC解算GPS监测数据,得到SNR观测值(L2载波)。限于篇幅,本文仅给出2012年第99天PRN21号卫星的解算结果,如图 3。针对小波分解层数的确定,通过多次实验确定分解层数为6,其重构结果见图 3(b)和图 3(c)。对比分析可得,采用方案1难以准确掌握SNR观测值的变化趋势,在卫星反射信号波动较小的时段极易偏离信号趋势,特别是在低卫星高度角时出现了显著偏差现象;而方案2能够很好地反映变化趋势。为进一步评定各方案的性能,本文采用均方根误差(RMSE)和平均绝对误差(MAE)两个指标。限于篇幅,只给出部分卫星拟合结果的RMSE和MAE(表 1)。结合图 3和表 1发现,方案2的精度指标总体均高于方案1的精度指标,小波分析方法相对于低阶多项式方法其RMSE至少提高了7.98%,MAE至少提高了25.2%。

|
图 3 PRN21号卫星的SNR观测值拟合趋势项 Fig. 3 SNR observation fitting trend term of PRN21 satellite |
|
|
表 1 两种方法的拟合精度统计 Tab. 1 Fitting accuracy statistics with two methods |
已有研究表明,土壤湿度的变化往往会引起卫星反射信号中物理参数的变化,相对相位延迟与土壤湿度存在良好的线性相关性[4]。因此,为了进一步验证小波分析在土壤湿度反演中的有效性,本文在方案1、方案2的基础上设置卫星截止高度角为5°~20°,采用最小二乘拟合的方法计算各卫星的相对相位延迟,以PBO提供的土壤水分产品作为参考值。限于篇幅,本文仅给出部分卫星的相对相位延迟与土壤湿度的关系(图 4)。
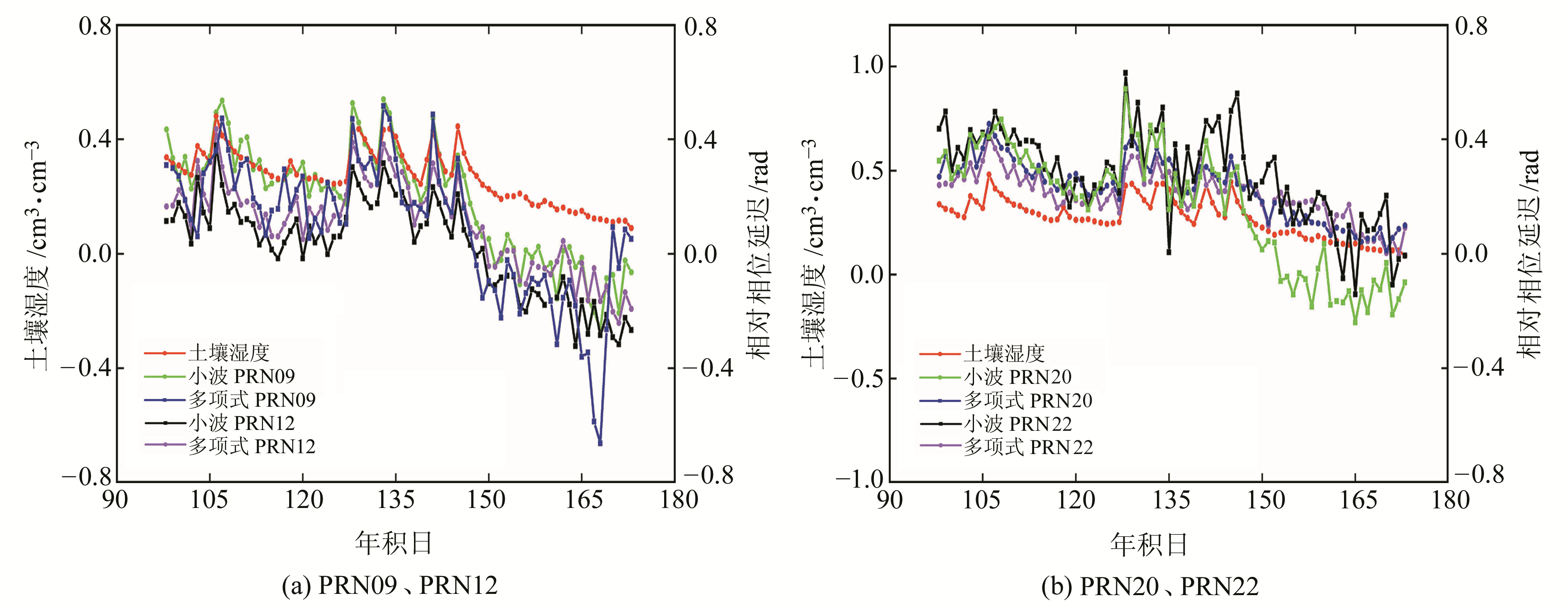
|
图 4 P041测站的相对相位延迟与土壤湿度的关系 Fig. 4 Relationship between relative delay phase and soil moisture of P041 station |
由图 4可见,整个时段内,当土壤湿度出现上升或下降波动时,各卫星的相对相位延迟均能作出响应。方案1所得相对延迟相位呈现出较大的跳变,比如图 4(a)中第167~168天PRN09号卫星和图 4(b)中第134~135天PRN20号卫星。而方案2能够很好地反映土壤湿度的变化趋势,局部分离效果较好,有效改善了采用低阶多项式进行分离时分离结果极易出现跳变的现象。
为进一步评定本文方法的综合性能,本文采用线性相关系数r进行评定(图 5、表 2)。限于篇幅,只给出PRN09、PRN22号卫星分别利用方案1、方案2所得的相对延迟相位与土壤湿度的线性拟合结果(图 5)。由图可见,线性回归方程(形如y=ax+b)能够较好地表示两者之间的关系。结合表 2发现,采用小波分析方法相对于二阶多项式方法,r至少提高了11.95%。采用小波分析的方法,不仅保证了各颗卫星拟合过程中局部误差的稳定性,而且有效提高了相对延迟相位与土壤湿度之间的相关性。

|
图 5 土壤湿度线性回归分析 Fig. 5 Linear regression analysis of soil moisture |
|
|
表 2 P041测站各卫星相位与土壤湿度的相关系数 Tab. 2 Correlation coefficient between satellite phase and soil moisture of P041 station |
本文提出基于小波分析的卫星反射信号分离方法,得出结论:在观测过程中,同一卫星不同年积日的SNR受测站天线周围环境、大气状况等因素影响,卫星直射信号的趋势往往存在差异,利用小波分析能有效提高卫星反射信号的分离精度,相对于低阶多项式拟合精度至少提高了7.98%;获取的相对延迟相位与土壤湿度之间的线性关系显著增强,相关系数至少提高了11.95%。
在分离卫星反射信号的研究中,还存在小波基的选择和分解层数的确定等问题,这需要在后续工作中进一步研究。
| [1] |
刘经南, 邵连军, 张训械, 等. GNSS-R研究进展及其关键技术[J]. 武汉大学学报:信息科学版, 2007(11): 955-960 (Liu Jingnan, Shao Lianjun, Zhang Xunxie, et al. Advances in GNSS-R Studies and Key Technologies[J]. Geomatics and Information Science of Wuhan University, 2007(11): 955-960)
(  0) 0) |
| [2] |
严颂华, 龚健雅, 张训械, 等. GNSS-R测量地表土壤湿度的地基实验[J]. 地球物理学报, 2011, 54(11): 2 735-2 744 (Yan Songhua, Gong Jianya, Zhang Xunxie, et al. Ground Based GNSS-R Observations for Soil Moisture[J]. Chinese Journal of Geophysics, 2011, 54(11): 2 735-2 744)
(  0) 0) |
| [3] |
Yu K G, Rizos C, Burrage D, et al. An Overview of GNSS Remote Sensing[J]. EURASIP Journal on Advances in Signal Processing, 2014, 134
(  0) 0) |
| [4] |
Larson K M, Small E E, Gutmann E D, et al. Use of GPS Receivers as a Soil Moisture Network for Water Cycle Studies[J]. Geophysical Research Letters, 2008, 35(24): 851-854
(  0) 0) |
| [5] |
Larson K M, Braun J J, Small L E E, et al. GPS Multipath and Its Relation to Near-Surface Soil Moisture Content[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2010, 3(1): 91-99 DOI:10.1109/JSTARS.2009.2033612
(  0) 0) |
| [6] |
Bilich A, Larson K M. Mapping the GPS Multipath Environment Using the Signal to Noise Ratio(SNR)[J]. Radio Science, 2007(42): 3-13
(  0) 0) |
| [7] |
Chew C, Small E E, Larson K M, et al. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 537-543 DOI:10.1109/TGRS.2013.2242332
(  0) 0) |
| [8] |
敖敏思, 胡友健, 刘亚东, 等. GPS信噪比观测值的土壤湿度变化趋势反演[J]. 测绘科学技术学报, 2012, 29(2): 66-69 (Ao Minsi, Hu Youjian, Liu Yadong, et al. Inversion of Soil Moisture Fluctuation Based on Signal-to-Noise Ratio of Global Positioning System[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 66-69)
(  0) 0) |
| [9] |
Wang X, Zhang Q, Zhang S. Water Levels Measured with SNR Using Wavelet Decomposition and Lomb-Scargle Periodogram[J]. GPS Solutions, 2018(1): 8
(  0) 0) |
| [10] |
Ren C, Liang Y J, Lu X J, et al. Research on the Soil Moisture Sliding Estimation Method Using the LS-SVM Based on Multi-Satellite Fusion[J]. International Journal of Remote Sensing, 2018(10): 1-16
(  0) 0) |
| [11] |
王祖林, 周荫清. 小波分析理论及其在雷达信号处理中的应用[J]. 北京航空航天大学学报, 1999(2): 10-13 (Wang Zulin, Zhou Yinqing. Wavelet Analysis Theory and Application in Radar Signal Processing[J]. Journal of Beijing University of Aeronautics and Astronautics, 1999(2): 10-13)
(  0) 0) |
| [12] |
丰秋林, 郑南山. 机器学习算法辅助的GPS信噪比观测值土壤湿度反演[J]. 测绘通报, 2018(7): 106-111 (Feng Qiulin, Zheng Nanshan. Retrieving Soil Moisture Using Signal-to-Noise Ratio of GPS Signal by Assisted Machine Learning Algorithm[J]. Bulletin of Surveying and Mapping, 2018(7): 106-111)
(  0) 0) |
| [13] |
罗甘, 梁月吉, 黄仪邦. 基于双树复小波的变形监测数据去噪分析[J]. 大地测量与地球动力学, 2018, 38(9): 958-963 (Luo Gan, Liang Yueji, Huang Yibang. Deformation Analysis Based on a Dual-Tree Complex Wavelet Transform Method[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 958-963)
(  0) 0) |
| [14] |
王旭, 王昶. 一种改进小波阈值去噪方法的研究[J]. 大地测量与地球动力学, 2017, 37(10): 1 038-1 041 (Wang Xu, Wang Chang. Improved Wavelet Threshold De-Noising Method Research[J]. Journal of Geodesy and Geodynamics, 2017, 37(10): 1 038-1 041)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2020, Vol. 40
2020, Vol. 40


