随着测量技术的发展，病态问题始终广泛地存在于大地测量数据处理中，如大地反演、控制网平差、GPS快速定位、重力场向下延拓、精密定轨、地震预报^[1]等。由于大地测量中存在大量的附加信息和先验信息^[2-3]，它们包含参数内在的相关性、精度、几何或物理信息，因此，解决病态问题的有效途径之一就是充分利用参数的附加信息或先验信息，对参数进行约束，从而保证整体解的唯一性和稳定性。许多学者研究了等式约束^[4-5]、不等式约束^[6-9]、随机线性约束^[10]、区间约束^[11]以及椭球约束^[12]等平差模型及算法，但所涉及的仅是最简单的情形，还不能处理更多的不确定性信息。附加信息对于病态问题的解决仍然不充分，对于一般的约束信息不仅要考虑它的病态性，还要考虑附加信息的有效性，以及降低病态性的效率。针对这些问题，本文将数学理论中参数优化方法^[13]转化为实际平差模型，利用先验信息对参数加以球约束，建立了带有球约束的平差模型，基于最优化理论将测量平差问题转化为凸二次规划问题，并提出解算方法。该方法考虑大地测量中的先验信息，提高了参数估计的精度。模拟数值实验和测边网实例应用结果显示，该方法在处理病态问题上具有明显的更优估计，可以广泛应用于大地测量病态数据处理。

1 球约束平差模型与岭估计

建立一般的平差模型：

$ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}}\ $

(1)

式中，L为观测向量；A为n×t的观测矩阵，A列满秩(R(A)=t)；X是t×1的未知向量；e是随机误差向量，期望为0(e ~(0，σ²Q)，Q为协因数矩阵)。

如果参数带有不确定性，我们对式(1)的参数X加以先验约束：

$ \left| {{\mathit{\boldsymbol{X}}_i}} \right| \le {r_i},i = 1, 2, \cdots , n $

(2)

得到参数带先验约束的平差模型：

$ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}}}\\ {{\rm{s}}.{\rm{t}}.\;\;\left| {{\mathit{\boldsymbol{X}}_i}} \right| \le {r_i}} \end{array}} \right. $

(3)

将式(3)变形，即得到参数带球约束的平差模型：

$ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}}}\\ {{\rm{s}}.{\rm{t}}.\;\;{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} \le {r^2}} \end{array}} \right. $

(4)

式中，L为观测向量；A为n×t观测矩阵，A列满秩(R(A)=t)；X是t×1的未知向量；e是随机误差向量，均值为0；协方差为σ²I，I为单位矩阵；S为正定矩阵；r为已知数且r≥0。

根据最小二乘准则，即${\left\| {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right\|^2}$最小，将式(4)转为带球约束的二次规划问题：

$ \left\{ {\begin{array}{*{20}{c}} {{\rm{min}}f\left( \mathit{\boldsymbol{X}} \right) = {{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\;{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{SX}}} \le {r^2}} \end{array}} \right. $

(5)

因为${\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right) = {\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{X}} + \left( { - 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}$，其中L^TL大于零；A为列满秩，那么A^TA为正定矩阵，故式(5)是一个凸二次规划问题，等价于：

$ \left\{ {\begin{array}{*{20}{c}} {{\rm{min}}f\left(\mathit{\boldsymbol{X}} \right) = \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{NX}} + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{X}}}\\ {{\rm{s}}.{\rm{t}}.\;\;\;{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} \le {r^2}} \end{array}} \right. $

(6)

式中，$\mathit{\boldsymbol{N}} = 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}$，$\mathit{\boldsymbol{c}}^{\rm{T}} = - 2{\mathit{\boldsymbol{A}}}^{\rm{T}}\mathit{\boldsymbol{L}}$。对式(6)使用拉格朗日乘数法得：

$ \begin{array}{l}\;\;\;\;\;\;\; \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}},\lambda } \right) = \\ \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{NX}} + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \frac{1}{2}\lambda \left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} - {r^2}} \right) \end{array} $

(7)

把式(7)分别对X和λ求偏导，分别令其等于0，得：

$ \left\{ {\begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{N}} + \lambda \mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{X}} = - {\mathit{\boldsymbol{c}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{X}}^{\rm{T}}}S\mathit{\boldsymbol{X}} = {r^2}} \end{array}} \right. $

(8)

故

$ \begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}} = - {(\mathit{\boldsymbol{N + }}\lambda S)^{ - 1}}{\mathit{\boldsymbol{c}}^{\rm{T}}}=\\ \;\;\;\;\;\;{({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{S}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} \end{array} $

(9)

注意到，当S = I时，有${{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}} = ({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \lambda {\mathit{\boldsymbol{I}}^{ - 1}}){\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}$，即为通常的岭估计。但这里λ不是常数，却依赖于样本。由式(9)左乘$({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{S}})$可得：

$ ({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{S}}){{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

那么，

$ \lambda \mathit{\boldsymbol{S}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}}} \right) $

在约束边界上${\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} = {r^2}$，有$\lambda {r^2} = \lambda \mathit{\boldsymbol{\hat X}}_{{\rm{GLS}}}^{\rm{T}}\mathit{\boldsymbol{S}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}} = \mathit{\boldsymbol{\hat X}}_{{\rm{GLS}}}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}}} \right)$, 因此有：

$ \lambda = \frac{1}{{{r^2}}}\mathit{\boldsymbol{\hat X}}_{{\rm{GLS}}}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\hat e}}}_{{\rm{GLS}}}} $

(10)

其中，${{\mathit{\boldsymbol{\hat e}}}_{{\rm{GLS}}}} = \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{GLS}}}}$。式(10)为岭参数的确定提供了一种新的途径。从式(10)可知，选取的岭参数要尽可能的小。容易验证，当用最小二乘估计${{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}$去估计式(10)中的参数λ时，有：

$ \begin{array}{l} \lambda = \frac{1}{{{r^2}}}\mathit{\boldsymbol{\hat X}}_{{\rm{LS}}}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}}} \right) = \\ \frac{1}{{{r^2}}}\left( {\mathit{\boldsymbol{\hat X}}_{{\rm{LS}}}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{\hat X}}_{{\rm{LS}}}^{\rm{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}}} \right) = 0 \end{array} $

故在设计阵A病态时，使用这种类似于两步估计的方法时应该格外小心，理论上已经表明，此时不宜采用广义最小二乘估计。

2 球约束平差的迭代算法

为便于解算，可将式(6)缩为一个更为简单的二次规划问题^[14]。记λ₁、λ₂分别为N的最小特征值和最大特征值，μ为S的最小特征根。对于任意的$\mathit{{\boldsymbol{X}}_k} \in \left\{ {\mathit{\boldsymbol{X}} \in {R^n}:{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{PX}} \le {r^2}} \right\}$，让θ=(λ₂+η)/μ(η≥0)，因为θS - N的特征根全都大于0，以(θS - N)为正定矩阵，得到：

$ \begin{array}{l} \frac{1}{2}{\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_k}} \right)^{\rm{T}}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right)\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_k}} \right) = \\ \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right)\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} + \\ \;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{X}}_k^{\rm{T}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} \ge 0 \end{array} $

所以，

$ \begin{array}{l} - \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right)\mathit{\boldsymbol{X}} \le - {\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} + \\ \;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{X}}_k^{\rm{T}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} \end{array} $

故

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;f\left( \mathit{\boldsymbol{X}} \right) = \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{N}}\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{X}} = \\ \;\;\;\;\;\;\frac{1}{2}\theta {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{S}}\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}^{\rm{T}}}\left[ {\frac{1}{2}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right)\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{c}}} \right] \le \\ \;\;\;\;\;\;\;\;\frac{1}{2}\theta {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} - {\mathit{\boldsymbol{X}}^{\rm{T}}}\left[ {\left( \theta {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right] + \\ \frac{1}{2} \mathit{\boldsymbol{X}}_k^{\rm{T}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} = \mathit{g}\left( \mathit{\boldsymbol{X}} \right) + \frac{1}{2}\mathit{\boldsymbol{X}}_k^{\rm{T}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} \end{array} $

其中，$\mathit{g}\left( \mathit{\boldsymbol{X}} \right) = \frac{1}{2}\theta {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} - \mathit{\boldsymbol{X}}_k^{\rm{T}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]$。

因为若X_k给定后，$\frac{1}{2}\mathit{\boldsymbol{X}}_k^{\rm{T}}\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k}$是一个定值，所以式(6)可转化为凸二次规划问题：

$ \left\{ {\begin{array}{*{20}{c}} {{\rm{min}}\;\;g\left( \mathit{\boldsymbol{X}} \right) = \frac{1}{2}\theta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{SX}}} - {\mathit{\boldsymbol{X}}^{\rm{T}}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\;\;\;{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{SX}} \le {r^2}} \end{array}} \right. $

(11)

令g(X)关于X的导数等于0，有：

$ \theta \mathit{\boldsymbol{SX}} - \left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right] = 0 $

可以得到g(X)的最小点为${\mathit{\boldsymbol{X}}_{{\rm{min}}}} = \frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta }$。设x_k+1是式(8)的一个解，当$\mathit{\boldsymbol{X}}_{{\rm{min}}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{{\rm{min}}}} \le {r^2}$时，${\mathit{\boldsymbol{X}}_{k + 1}} = \frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta }$；当$\mathit{\boldsymbol{X}}_{{\rm{min}}}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{{\rm{min}}}} > {r^2}$时，问题的约束解在边界上取得^[14]，将其在球面上投影，得到${\mathit{\boldsymbol{X}}_{k + 1}} = \frac{{{\mathit{\boldsymbol{X}}_{{\rm{min}}}}}}{{\left\| {{\mathit{\boldsymbol{X}}_{{\rm{min}}}}} \right\|}}r = \frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{{\left\| {{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]} \right\|}}r$，即

$ {\mathit{\boldsymbol{X}}_{k + 1}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta },}\\ {\left\| {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta }} \right\| \le r}\\ {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{{\left\| {{S^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]} \right\|}}r,}\\ {\frac{{\left\| {{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]} \right\|}}{\theta } > r} \end{array}} \right. $

(12)

因为X_k+1是式(11)的一个解，所以X_k+1满足式(11)的KT条件：

$ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \theta \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} - \left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right] + \\ {\lambda _{k + 1}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} = 0 \end{array}\\ {{\lambda _{k + 1}}\left( {\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} - {r^2}} \right) = 0} \end{array}} \right. $

(13)

式中，λ_k+1为Lagrange乘子。显然，$\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} \le {r^2}(\mathit{k} = 1,2, \cdots )$,{X_k}和{f(X_k)}是有界的。不失一般性，设$\mathop {{\rm{lim}}}\limits_{_{k \to \infty }} {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{X}}^*}$，若$\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} < {r^2}$，则λ_k+1=0；若$\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}_{k + 1}} = {r^2}$，则在式(13)两边乘以$\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}$，得：

$ \theta {r^2} - \mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right] + {\lambda _{k + 1}}{r^2} = 0 $

所以有：

$ {\lambda _{k + 1}} = \frac{{{{\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{k + 1}} - \theta {r^2}}}{{{r^2}}} $

因此，

$ \begin{array}{l} \;\;\;\;\;\;\;{\lambda ^{\rm{*}}} = \mathop {\lim }\limits_{k \to \infty } {\lambda _{k + 1}} = \\ \frac{{{{\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{k + 1}} - \theta {r^2}}}{{{r^2}}} = \\ \;\;\;\;\;\;\frac{{ - {{({\mathit{\boldsymbol{X}}^*})}^{\rm{T}}}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{X}}^*} - {\mathit{\boldsymbol{c}}^{\rm{T}}}{\mathit{\boldsymbol{X}}^*}}}{{{r^2}}} \end{array} $

即有：

$ {\lambda ^{\rm{*}}} = \left\{ {\begin{array}{*{20}{c}} {{\lambda ^{\rm{*}}},{{({\mathit{\boldsymbol{X}}^*})}^{\rm{T}}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}^*} = {r^2}}\\ {0,{{({\mathit{\boldsymbol{X}}^*})}^{\rm{T}}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}^*} < {r^2}} \end{array}} \right. $

对式(13)两边取极限，得：

$ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{X}}^*} + \mathit{\boldsymbol{c}} + {\lambda ^{\rm{*}}}{\mathit{\boldsymbol{X}}^*} = 0}\\ {\frac{1}{2}{\lambda ^{\rm{*}}}\left( {{{({\mathit{\boldsymbol{X}}^*})}^{\rm{T}}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{X}}^*} - {r^2}} \right) = 0} \end{array}} \right. $

(14)

式(14)恰好是式(6)的KT条件，X^*为式(6)的一个KT点，λ^*为Lagrange乘子。因此，设X₀∈Rⁿ为任意给定的一点，迭代公式(11)产生的点列{X_k}的每一个聚点都是式(6)的KT点。

下面给出带球约束的平差算法的步骤。

1) 利用先验信息确定球约束半径r；

2)${\mathit{\boldsymbol{X}}_0} \in \left\{ {\mathit{\boldsymbol{X}} \in {R^n}:\left\| \mathit{\boldsymbol{X}} \right\| \le r} \right\}$，让θ=(λ₂+η)/μ(η≥0)，k=0，ε>0；

3) $\begin{array}{l} {\mathit{\boldsymbol{X}}_{k + 1}} = \\ \left\{ {\begin{array}{*{20}{\mathit{\boldsymbol{c}}}} {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta },}\\ {\left\| {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta }} \right\| \le r}\\ {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{{\left\| {{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]} \right\|}}r,}\\ {\left\| {\frac{{{\mathit{\boldsymbol{S}}^{ - 1}}\left[ {\left( {\theta \mathit{\boldsymbol{S}} - \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{c}}} \right]}}{\theta }} \right\| > r} \end{array}} \right. \end{array}$

4) 若$\left\| {{\mathit{\boldsymbol{X}}_{k + 1}} - {\mathit{\boldsymbol{X}}_k}} \right\| \le \varepsilon $，停止，输出X^*= X_k+1；否则k=k+1，转步骤1)。

3 算例分析 3.1 数值模拟实验

为了验证球约束在测量平差中的实用性，采用文献[15]的数据进行计算：

$ \left[ {\begin{array}{*{20}{c}} 1&{\frac{1}{2}}&{\frac{1}{3}}&{\frac{1}{4}}\\ {\frac{1}{2}}&{\frac{1}{3}}&{\frac{1}{4}}&{\frac{1}{5}}\\ {\frac{1}{3}}&{\frac{1}{4}}&{\frac{1}{5}}&{\frac{1}{6}}\\ {\frac{1}{4}}&{\frac{1}{5}}&{\frac{1}{6}}&{\frac{1}{7}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ {{x_4}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{25}}{{12}}}\\ {\frac{{77}}{{60}}}\\ {\frac{{19}}{{20}}}\\ {\frac{{319}}{{420}}} \end{array}} \right] $

该矩阵cond(N)=1.55×10⁴，方程组病态性严重。其真值$\mathit{\boldsymbol{\hat x}} = \left[ {1\;\;\;1\;\;\;1\;\;\;1} \right]$，在常数向量中通过Matlab加入σ²=0.05微小误差，得到L =[2.077 2 1.271 5 0.976 6 0.789 0]^T。由于已知真值和误差扰动，直接取${r^2} = {{\mathit{\boldsymbol{\hat x}} \mathit{\boldsymbol{\hat x}}}^{\rm{T}}} + {\sigma ^2} = 4.05$，分别采用最小二乘、岭估计、椭球约束以及本文的球约束方法求解，结果如表 1所示。

此法方程系数矩阵N的条件数过大，导致函数模型病态，最小二乘解偏离真值较大，严重失真，而加入一些先验信息可以显著改善其病态性。从表 1结果可以看出，在椭球约束和球约束的条件下，解向量与真值之间的二范数的差值相对较小，且都优于岭估计和最小二乘平差。在球约束下解向量与真值之间的二范数仅为0.135 4，在上述估计中属于最优估计。因此，在建立平差模型时充分利用参数的先验信息可以弥补观测不充分导致的病态问题。

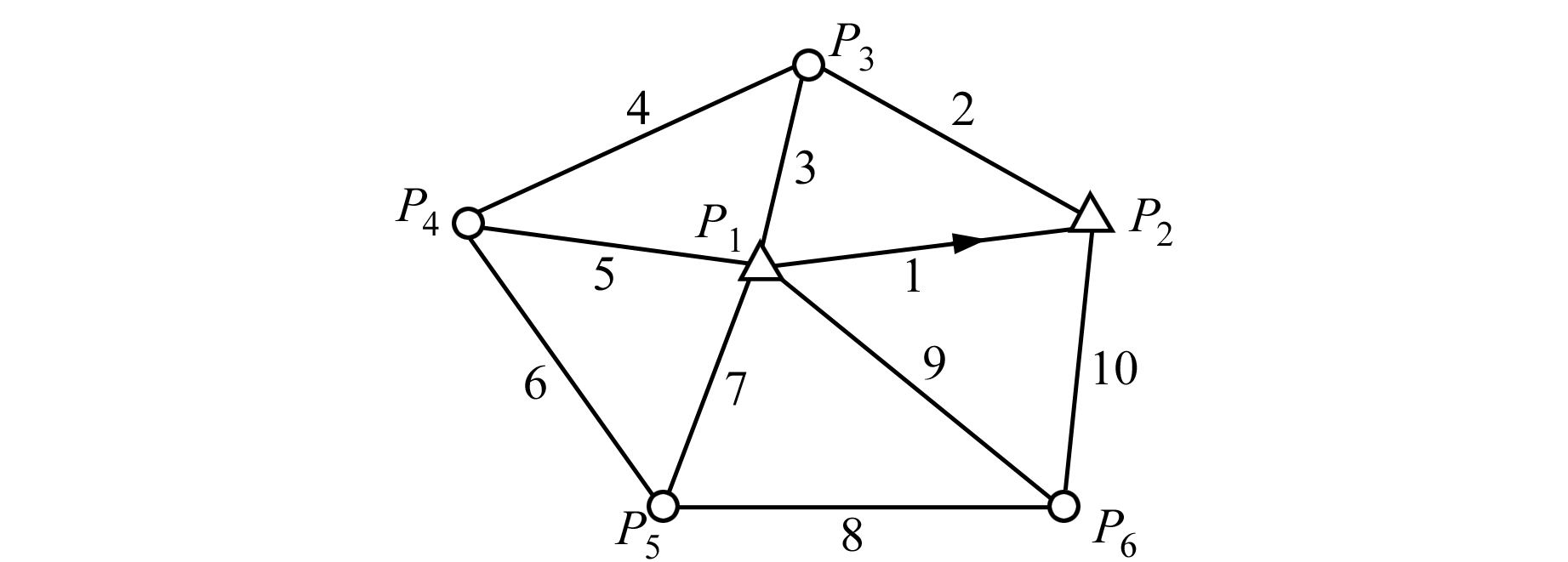
3.2 病态测边网实验 3.2.1 算例1

如图 1所示的测边网，P₁、P₂为已知点，其坐标分别为(48 580.285, 600 500.496)和(47 943.013, 66 225.845)。为了便于分析比较，算例中的点P₃、P₄、P₅、P₆的真实坐标假设已知(表 2)，边长的观测值是利用真实坐标计算，再通过Matlab加上σ²=0.05的随机误差得到的，其中边1是已知边，观测边长视为同精度(表 3)。为便于分析，假设前期观测得到P₃、P₄、P₅、P₆的近似坐标(表 2)。

目标函数为：$F\left( \mathit{\boldsymbol{X}} \right) = {\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)\;$, 误差平方和的计算公式为：$\mathit{m} = {\left( {\mathit{\boldsymbol{\hat X}} - \mathit{\boldsymbol{X}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{\hat X}} - \mathit{\boldsymbol{X}}} \right)$。相对于近似坐标的改正数构成的未知向量为$\mathit{\boldsymbol{X}} = {\left[ {{x_3},{y_3},{x_4},{y_4},{x_5},{y_5},{x_6},{y_6}} \right]^{\rm{T}}}$，可以得到相应的平差模型的系数矩阵和观测向量：

$ \begin{array}{l} {\mathit{\boldsymbol{A}}_1} = \\ \left[ {\begin{array}{*{20}{c}} {0.7434}&{ - 0.6689}&0&0&0&0&0&0\\ {0.9952}&{0.0975}&0&0&0&0&0&0\\ {0.6457}&{0.7636}&{ - 0.6457}&{ - 0.7636}&0&0&0&0\\ 0&0&{0.0183}&{ - 0.9998}&0&0&0&0\\ 0&0&{0.8575}&{ - 0.5145}&{ - 0.8575}&{0.5145}&0&0\\ 0&0&0&0&{ - 0.8848}&{ - 0.4660}&0&0\\ 0&0&0&0&{0.3904}&{ - 0.9206}&{ - 0.3904}&{0.9206}\\ 0&0&0&0&0&0&{ - 0.8708}&{0.4917}\\ 0&0&0&0&0&0&{ - 0.9823}&{ - 0.1874} \end{array}} \right]\\ ,{\mathit{\boldsymbol{L}}_1} = \left[ {\begin{array}{*{20}{c}} {1.4955}\\ { - 0.7877}\\ { - 2.5966}\\ {0.5178}\\ {3.7201}\\ {0.2180}\\ { - 6.2599}\\ { - 3.3892}\\ { - 1.7623} \end{array}} \right] \end{array} $

进行最小二乘计算，取最小二乘解的模，使$r = \sqrt {{{\mathit{\boldsymbol{\hat X}}}_\mathit{L}}\mathit{\boldsymbol{\hat X}}_\mathit{L}^{\rm{T}}} = 5.5$，内部迭代算法的终止条件设置为$\left| {{\mathit{\boldsymbol{X}}_k} - {\mathit{\boldsymbol{X}}_{k - 1}}} \right| < 0.000\;01$。

算例1显示，在系数矩阵列满秩的情况下，由于目标函数是凸函数，故存在唯一的最优解。从表 4可以看出，最小二乘解和本文算法解是一致的，真值与最优解基本相同，说明对于非病态的法方程矩阵，因为观测信息充分，不需要补充先验信息。

3.2.2 算例2

修改算例1中已知点P₂的坐标为(48 570.013, 60 555.845)，使它非常靠近P₁点，导致系数矩阵病态，用来分析病态问题中算法的性能。此时相应的边长观测也会发生变化(表 5)，相应的平差模型的系数矩阵和观测向量为：

$ \begin{array}{l} {\mathit{\boldsymbol{A}}_1} = \\ \left[ {\begin{array}{*{20}{c}} {0.9958}&{0.0920}&0&0&0&0&0&0\\ {0.9952}&{0.0975}&0&0&0&0&0&0\\ {0.6457}&{0.7636}&{ - 0.6457}&{ - 0.7636}&0&0&0&0\\ 0&0&{0.0183}&{ - 0.9998}&0&0&0&0\\ 0&0&{0.8575}&{ - 0.5145}&{ - 0.8575}&{0.5145}&0&0\\ 0&0&0&0&{ - 0.8848}&{ - 0.4660}&0&0\\ 0&0&0&0&{0.3904}&{ - 0.9206}&{ - 0.3904}&{0.9206}\\ 0&0&0&0&0&0&{ - 0.8708}&{0.4917}\\ 0&0&0&0&0&0&{ - 0.8710}&{0.4913} \end{array}} \right]\\ ,{\mathit{\boldsymbol{L}}_2} = \left[ {\begin{array}{*{20}{c}} { - 0.7351}\\ { - 0.7877}\\ { - 2.5966}\\ {0.5178}\\ {3.7201}\\ {0.2180}\\ { - 6.2599}\\ { - 3.3892}\\ { - 3.3113} \end{array}} \right] \end{array} $

在实际应用中，由于误差的随机性和参数真值的未知性，这里取$r = \sqrt {\frac{{{{\mathit{\boldsymbol{\hat X}}}_{{\rm{TSVD}}}}\mathit{\boldsymbol{\hat X}}_{{\rm{TSVD}}}^{\rm{T}} + {{\mathit{\boldsymbol{\hat X}}}_{{\rm{RE}}}}\mathit{\boldsymbol{\hat X}}_{{\rm{RE}}}^{\rm{T}}}}{2}} = 5.335$，取自截断奇异值法解与岭估计法(L曲线法)解的平均值。内部迭代算法的终止条件设置为$\left| {{\mathit{\boldsymbol{X}}_k} - {\mathit{\boldsymbol{X}}_{k - 1}}} \right| < 0.000\;01$。

算例2中，$\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}$是一个正定矩阵(此例中P为单位矩阵)，但有一个特征值接近0，N的条件数cond(N)=1.353 3×10⁶，属于法方程病态，这时最小二乘解明显偏离真值。加入球约束后的计算结果显示，已经产生了一个有效约束，且有效约束显著改善了模型的病态性。而最小二乘解其估计${{\mathit{\boldsymbol{\hat X}}}_{{\rm{LS}}}}$不在约束区间内，与先验信息明显不符，严重失真。这说明当平差模型出现严重病态时，加入区间约束可以显著改善其病态性。

从计算结果来看(表 6)，虽然最小二乘解的目标函数最小值最小，仅为0.003 3，但其误差平方和却达到147以上，严重偏离真值。在使用通常针对病态问题的解法(截断奇异值、岭估计)计算时，结果有明显的改善，其误差平方和得到极大降低，分别降低到1.312 0和1.181 8。但利用先验信息对其加以球约束后，从本文的算法解可以看出，本文解已经极其逼近真值，且残差平方和为1.064 4。此算例说明，利用参数的先验约束信息建立球约束平差模型，可以改善平差模型的病态性。因此，在建立平差模型时充分利用参数的先验信息，可以弥补观测不充分导致的病态问题。

4 结语

大地测量中，参数的先验信息往往反映了被观测目标的几何物理特征、测量精度以及参数相关性等。数据处理时，利用这些先验信息在一般的平差模型中对参数加以约束，可以改善模型的不适定性，以提高解的精确性和可靠性。本文两个实例均为病态实验，由于法方程的病态性导致了最小二乘解严重失真，但是在加入球约束后，解的精度有明显提高，说明本文所阐述的带球约束的平差算法是可行的。在大地测量中，通常会因为观测限制和观测成本高而造成数据不充分，所以本文算法对提高参数估计的效率有非常大的实际意义。其次，可以对近代测量平差的研究范围进行扩充，也有重要的理论意义。