随着GPS技术的发展,采用GPS观测数据后处理估计的天顶对流层延迟(ZTD)可达mm级精度,而各地区域GPS观测网的建立,也为区域对流层延迟的高精度建模奠定了基础。在区域对流层延迟的高精度建模中,如何利用参考站的对流层延迟得到待插值站的对流层延迟是一个关键问题。常规的内插算法主要有线性内插法(LIM)、线性组合法(LCM)、反距离加权插值法(IDW)、低阶趋势面法(LSM)和最小二乘配置算法(LSC)等,这些算法的内插效果没有明显的区别[1],且在地形起伏较大区域适应性较差,当高差达到1 km左右时,对流层延迟偏差可达9 cm[2]。文献[3]对比分析了不同的ZTD空间回归模型的内插效果,提出采用高差约束的方法减少高差较大造成的内插精度损失;文献[4]提出基于经验模型的移去-恢复法,该法一定程度上能够弥补传统内插方法的缺陷,但当高差较大时(如数km以上),其效果仍然不理想[5];文献[5]提出投影延拓法,该法能避免高差较大带来的空间结构上的畸形,在高差达到2 km时也有较优的改善效果,但该法的精度主要依赖于经验对流层模型在垂直方向上的分辨率误差,若其误差较大,则需要获取测区对流层垂直方向上的实时大气参数;文献[6]提出基于EGNOS模型的反距离加权插值法,该法通过对EGNOS模型中的ZTD计算公式求导得到ZTD随高程的变化率,并依据该变化率将ZTD在高程方向上投影延拓,在高差较大时内插精度得到明显改善。
本文通过对比分析数值天气模型(NWM)的ZTD垂直剖面的不同拟合形式,确定适用于GPS测站投影延拓模型的高精度垂直剖面函数。在此基础上,提出基于ZTD垂直剖面函数的对流层延迟插值算法。通过与传统内插算法的比较分析显示,该算法能够有效提高ZTD插值的精度。
1 基于垂直剖面函数的ZTD插值算法 1.1 空间回归模型空间回归模型[3]的主要思想是:将测站的ZTD表达为经度、纬度和大地高的多项式,根据参考站已知的ZTD、经纬度及大地高建立误差方程,再由最小二乘法拟合出多项式系数,最后根据拟合的系数计算出待插值站ZTD。空间回归模型的表达形式随着多项式阶数的不同而存在差异,本文选取内插精度较高、相对稳定且形式简单的空间回归模型与本文提出的算法进行对比分析,其表达形式为:
| $ \mathrm{ZTD}=a_{0} B+a_{1} L+a_{2} H+a_{3} $ | (1) |
式中,ai为回归系数,B、L、H分别为纬度、经度和大地高。
1.2 ZTD垂直剖面函数的最佳拟合ERA-Interim是欧洲中尺度天气预报中心(ECMWF)提供的最新的全球大气再分析产品,利用该产品提供的格网气象元素可以计算得到对流层延迟。ERA-Interim资料的气压分层数据集的平面分辨率为0.75°×0.75°,时间分辨率为6 h,每个格网点包括37个等压层下的位势高度、温度、比湿和相对湿度等气象元素,最顶层的高度接近50 km,高于此高度的大气中水蒸气含量很低,其对流层湿延迟的影响可以忽略。ECMWF提供的位势高度是位势与重力加速度的比值,而GPS测站得到的是大地高,为便于采用垂直剖面函数对GPS测站得到的对流层延迟进行投影延拓,需将位势高转化为大地高[7]。将位势高转换为大地高后,可利用各层气象参数计算大气折射率,再对各层大气折射率在垂直高度上积分,最终可以获得ZTD在每个格网点上的垂直剖面。为提高积分法得到的对流层延迟的精度,在计算各层大气折射率时,各层的气象参数应取相邻2个等压面气象参数的均值[7]。采用积分法计算格网点ZTD垂直剖面的公式为:
| $ N = {k_1}\frac{{P - e}}{T} + {k_2}\frac{e}{T} + {k_3}\frac{e}{{{T^2}}} $ | (2) |
| $ e = hP/0.622 $ | (3) |
| $ Z{\rm{T}}{{\rm{D}}_i} = {10^{ - 6}}\int_s N {\rm{d}}s = {10^{ - 6}}\sum\limits_1^i {{N_i}} \Delta {s_i} $ | (4) |
式中,k1=77.604 K/hPa,k2=64.79 K/hPa, k3=337 600 K2/hPa, N为总大气折射率,P为大气压(hPa),e为水汽压(hPa),T为温度,h为比湿,ZTDi为自顶层开始的第i层高度下的天顶对流层延迟,Ni、Δsi分别为第i层的折射率和高度差。此外,为降低积分计算的ZTD的误差,采用Saastamonienon模型计算气压分层数据顶层之上的对流层天顶干延迟(ZHD), 将顶层之上的ZHD与各层积分ZTDi相加,得到各层最终的ZTD。
为分析ZTD在垂直剖面上随高度变化的规律,基于上述方法,计算获得了2017-02北欧地区(35°~55°N,0°~25°E)1°×1°格网点上ZTD剖面的时间序列,时间分辨率为6 h,每个垂直剖面包括37层ZTD数据。传统的剖面函数形式有二阶多项式[8]和指数函数[9],能在一定程度上较好地反映出ZTD垂直方向上的变化特点,但在较大高程范围内采用单一的函数表示ZTD会引起最大约5 cm的系统偏差[10]。文献[10]采用分段函数描述ZTD在垂直方向上的变化规律,在不同的高程范围内均得到较高的精度,但由于近地面水汽变化的复杂性,其近地面的偏差依然较大。由于GPS参考站的高程大多小于5 km,故而研究近地面ZTD的高精度剖面函数对GPS参考站的ZTD精准垂直缩放有重要意义。
对流层顶的高度随纬度和季节的变化而变化,其在夏季高于冬季,在赤道附近为16~18 km,在中纬度地区为10~12 km,两极附近为8~9 km[11]。水汽在对流层内不同高度的下降速率不同,约有50%的水汽集中在地面附近1.5 km以内,而5 km以上的水汽含量不足10%[12]。文献[10]的分段剖面函数以5 km和17 km作为分段点将ERA-Interim资料覆盖的50 km大气分为3个高度区间,但其在近地面拟合ZTD的偏差仍然较大。因本文的实验数据取自中纬度地区,且为更好地拟合近地面ZTD随高度的变化,同时考虑到大气中水汽的上述变化规律,经过实验对比分析,确定以3 km和11 km作为分段点的50 km大气的3个高度区间。由于在对流层顶以下使用两个三次多项式,在对流层顶以上使用指数函数拟合ZTD的效果较好[10], 且高斯函数在拟合ZTD剖面时优于指数函数模型[13],故本文采用两个三次多项式和高斯函数构建适用于GPS参考站ZTD投影延拓的高精度分段剖面函数:
| $ \text { ZTD }=\left\{\begin{aligned} p_{1} H^{3}+p_{2} H^{2}+p_{3} H+p_{4} ,\\ H \leqslant 3 \mathrm{km} \\ m_{1} H^{3}+m_{2} H^{2}+m_{3} H+m_{4} ,\\ 3 \mathrm{km} <H \leqslant 11 \mathrm{km} \\ n_{1} \exp \left(-\left(\frac{H-n_{2}}{n_{3}}\right)^{2}\right), H>11 \mathrm{km} \end{aligned}\right. $ | (5) |
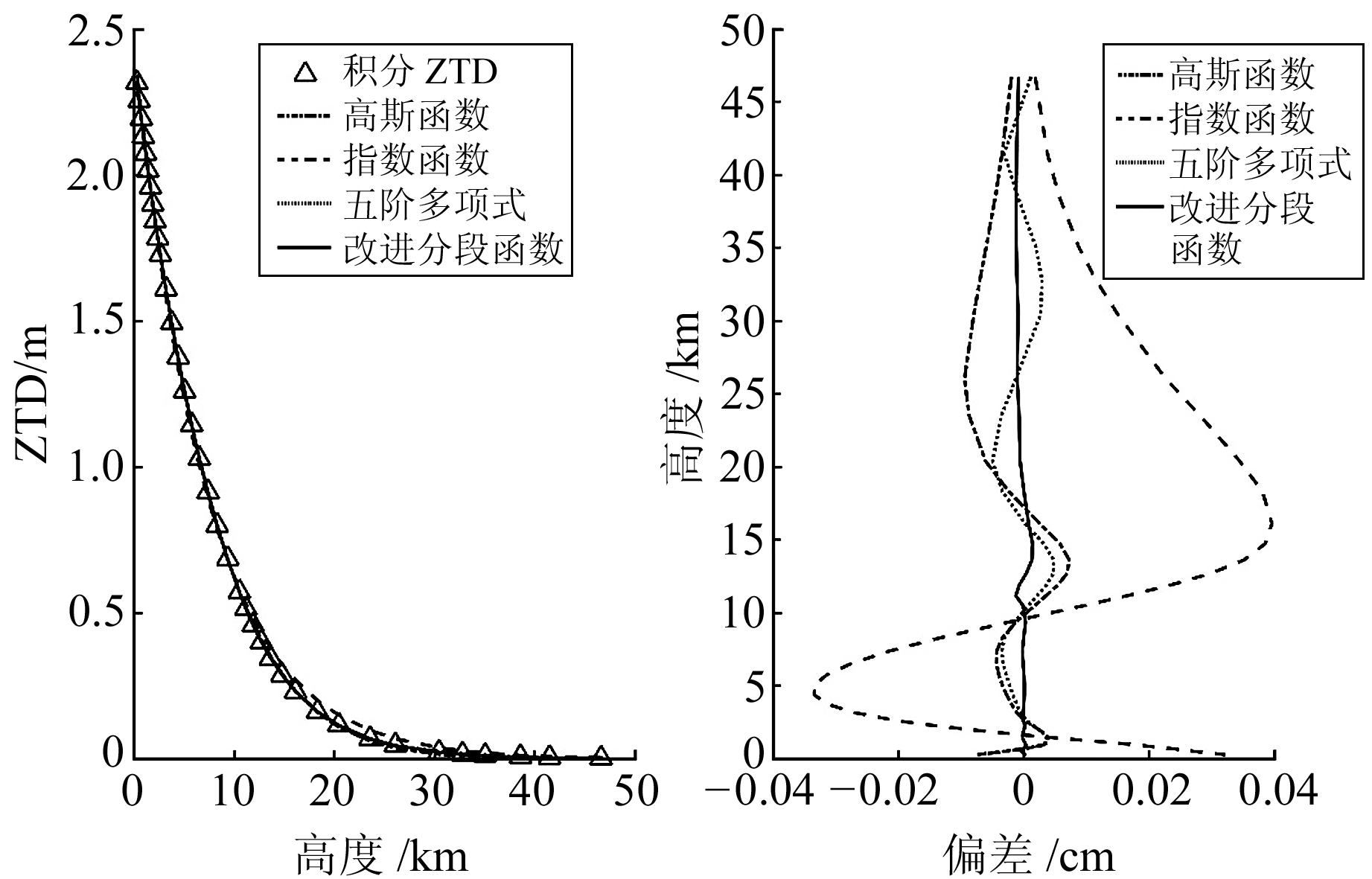
式中,pi、mi、ni(i=1, 2, 3, 4)为剖面函数的待求系数,H为大地高。该函数在近地面拟合的偏差为mm级,测区内所有格网点的平均RMS为0.6 mm。对比分析五阶多项式、指数函数、高斯函数[13]以及本文提出的分段函数的拟合效果,图 1为测区范围内随机选取的一个格网点的拟合结果和相对于积分ZTD的偏差。可以明显看出,分段剖面函数相对于其他3种函数形式具有明显的优势,且在不同的高度都有较好的一致性,尤其是在近地面也可满足mm级的内符合精度。
|
图 1 4种剖面函数拟合格网点(12°E, 45°N)ZTD的结果和偏差(2017-02-15 06:00 UTC) Fig. 1 Results and bias of grid point(12°E, 45°N) fitting by four profile functions(2017-02-15 06:00 UTC) |
传统的空间回归法形式简单、适应性强,但其在高差较大区域的插值精度较差,而高精度的ZTD垂直剖面函数能够为ZTD提供在高程方向上高精度的垂直缩放。结合两者的特点,本文提出基于垂直剖面函数的对流层插值算法。首先,通过式(2)~(4)积分得到各格网点的ZTD垂直剖面,再由式(5)拟合各格网点的剖面函数系数,参考站和待插值站的剖面函数系数可通过对其所在网格的4个角点采用双线性插值得到;然后,由参考站的ZTD剖面函数系数将参考站ZTD投影到平均高程面,再在平均高程面上采用空间回归法进行内插。由于平均高程面上各参考站的高程相同,故而空间回归模型可简化为:
| $ \mathrm{ZTD}=a_{0} B+a_{1} L+a_{2} B L+a_{3} $ | (6) |
最后,由待插值站的剖面函数系数将其在平均高程面上的ZTD延拓到目标高程面上,即得最终的ZTD。利用ZTD垂直剖面函数进行投影和延拓的表达式分别为:
| $ \mathrm{ZTD}_{r}^{m}=\mathrm{ZTD}_{r}·\\ \frac{\left(p_{1} H_{m}^{3}+p_{2} H_{m}^{2}+p_{3} H_{m}+p_{4}\right)}{\left(p_{1} H_{r}^{3}+p_{2} H_{r}^{2}+p_{3} H_{r}+p_{4}\right)} $ | (7) |
| $ Z \mathrm{TD}_{u}=Z \mathrm{TD}_{u}^{m}·\\ \frac{\left(p_{1} H_{u}^{3}+p_{2} H_{u}^{2}+p_{3} H_{u}+p_{4}\right)}{\left(p_{1} H_{m}^{3}+p_{2} H_{m}^{2}+p_{3} H_{m}+p_{4}\right)} $ | (8) |
式中,ZTDrm、ZTDum分别为参考站和待插值站投影到平均高程面上的天顶对流层延迟,ZTDr为参考站的天顶对流层延迟,ZTDu为延拓到待插值站高程面的最终天顶对流层延迟,pi同式(5),Hm、Hr、Hu分别为平均高程面高程、参考站高程和待插值站高程。限于篇幅,此处仅给出H≤3 km的投影延拓表达式,高于3 km的可依据式(5)、式(7)和式(8)同理推出。
本文插值算法的主要数据处理流程如图 2。

|
图 2 插值算法流程 Fig. 2 Interpolation algorithm flow |
算例采用欧洲40°~54°N、5°~13°E区域内IGS站提供的ZTD数据,选取的数据时间为2017-02-01~02-28,历元间隔为5 min。ECMWF数据集为2017-02的格网数据,格网密度为1°×1°,时间分辨率为6 h。为检验基于ZTD垂直剖面函数的对流层插值算法的实际效果,以待插值站高程与参考站平均高程面的高差大小为标准,选取3组IGS站(图 3)进行实验,并与反距离加权插值法和空间回归法(式(1))进行对比分析。

|
图 3 IGS测站的分布 Fig. 3 Distribution of IGS stations |
第1组IGS站以gras作为待插值测站,wab2、zimm、ieng、geno、ajac和mars为参考站,待插值站与参考站的平均高程面高差为1 011.22 m,删除IGS站ZTD数据缺失的864个历元后,共计7 200个历元;第2组IGS站以geno为待插值站,ieng、bzrg、medi、ajac和gras为参考站,待插值站与参考站的平均高程面高差为-285.74 m,删除IGS站ZTD数据缺失的288个历元后,共计7 776个历元;第3组IGS站以ffmj为待插值测站,wsrt、ptbb、leij、bzrg、hueg和wab2为参考站,待插值站与参考站的平均高程面高差为-90.6 m,删除IGS站ZTD数据缺失的864个历元后,共计7 200个历元。
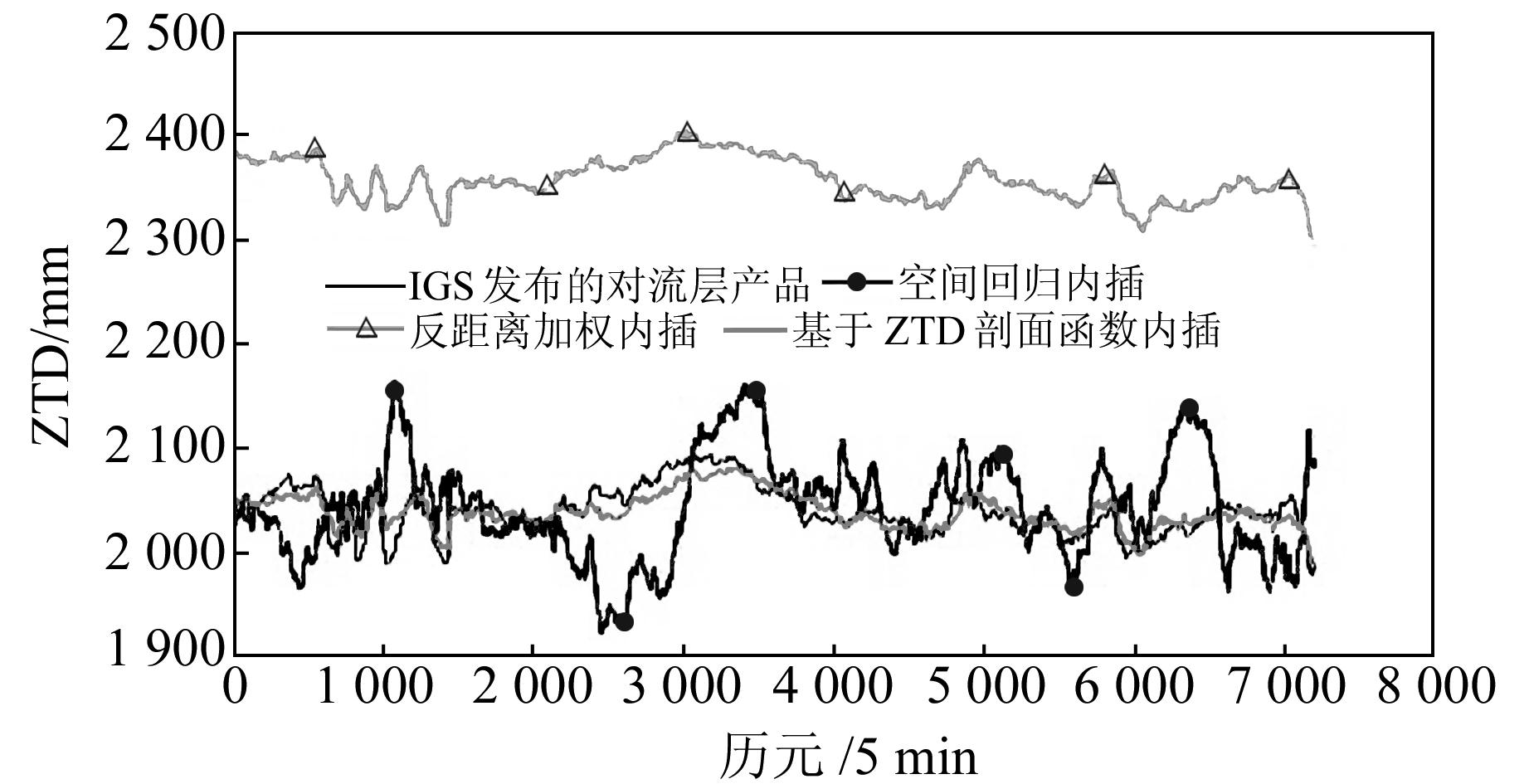
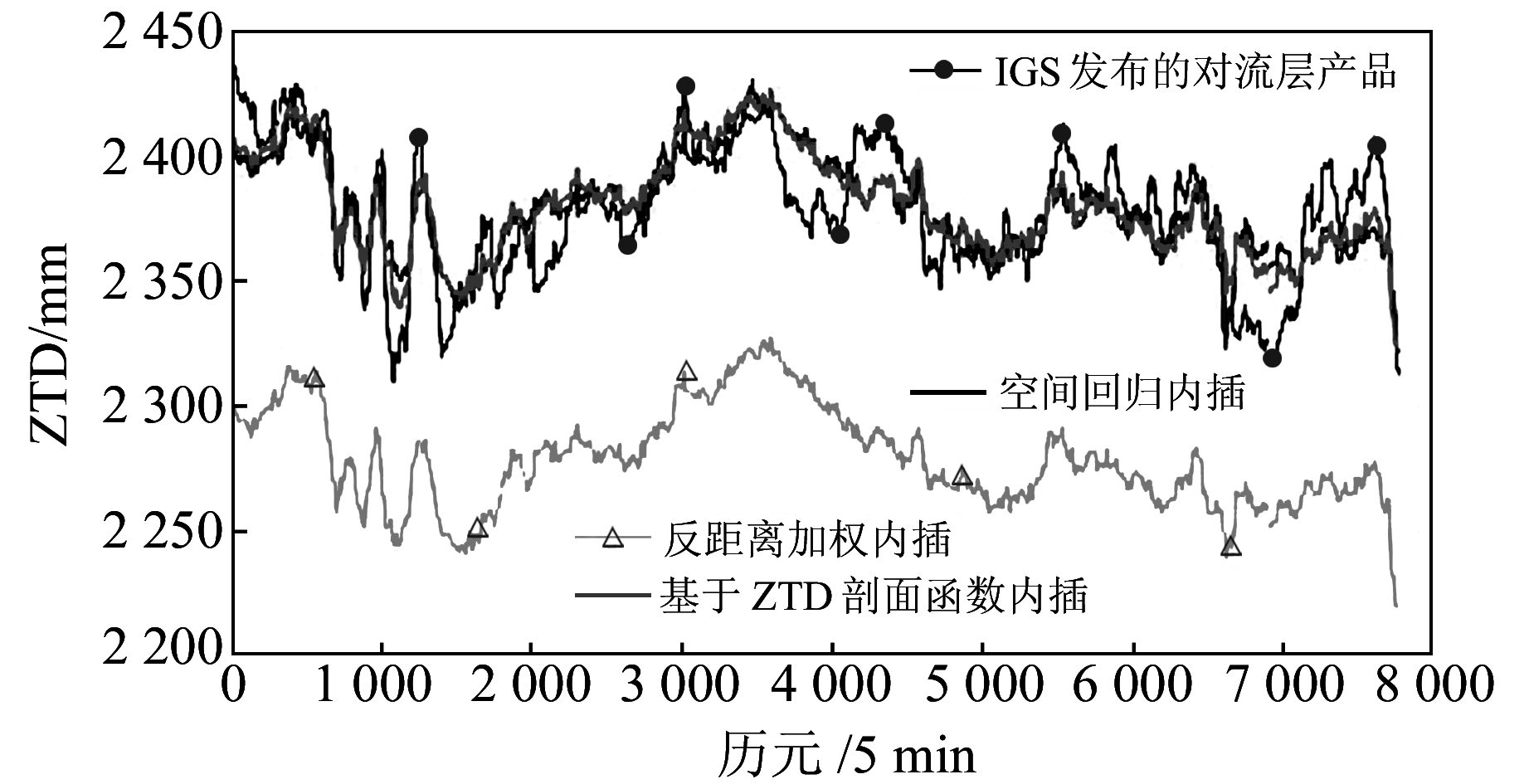
2.2 实验结果分析将解算得到的待插值站ZTD与IGS发布的最终对流层延迟产品进行比较,即可反映出内插的效果。图 4、图 5和图 6分别为gras、geno和ffmj的插值结果。可以明显看出,基于垂直剖面的ZTD插值改进算法相较于反距离加权内插法,两个测站的内插精度都有显著提高,尤其是高差较大的gras站,精度从dm级提升到cm级;空间回归法在3个测站的精度可以达到cm级甚至mm级;基于ZTD垂直剖面的插值算法虽然在高差相对较小的geno和ffmj测站的精度与空间回归法基本相当,但在高差较大的gras测站其结果更稳定,且精度要明显优于空间回归法。
|
图 4 测站gras的插值结果 Fig. 4 Interpolation results of station gras |
|
图 5 测站geno的插值结果 Fig. 5 Interpolation results of station geno |

|
图 6 测站ffmj的插值结果 Fig. 6 Interpolation results of station ffmj |
表 1罗列了3种方法计算的内插值相对于IGS对流层产品的均方根误差(RMS)。可以看出,反距离加权插值法的精度最差,在高差最大的gras站,RMS达到316.6 mm,难以满足高精度测量的要求;空间回归法在高差较小的测站精度较高,在高差小于100 m的ffmj测站RMS可达mm级,但随着高差的增大,精度下降明显,在高差超过1 km的gras测站RMS已达到53.7 mm;基于垂直剖面的ZTD插值改进算法能够有效克服高差过大带来的ZTD内插精度损失,在高差较小时能够获得和空间回归法相当的精度,在高差较大的gras测站,RMS为11.3 mm,该精度相对于反距离加权插值法提升了96%,相对于空间回归法提升了79%。
|
|
表 1 3种插值方法的精度比较 Tab. 1 Accuracy comparison of three interpolation methods |
本文针对在高差变化较大区域采用传统插值算法插值ZTD时精度下降、难以满足高精度定位需求的问题,基于ERA-Interim气压分层数据的ZTD垂直剖面函数,提出基于垂直剖面函数的ZTD插值算法。该算法依赖高精度的ZTD垂直剖面函数实现ZTD在高程方向上的准确缩放,通过将参考站ZTD投影到平均高程平面上进行插值,有效削弱了高差较大对ZTD插值的影响,相对于传统算法显著提高了插值精度,尤其在高差超过1 km时,精度相对于反距离加权插值法提高了96%,相对于空间回归法提升了79%。
目前,由于ERA-Interim数据的滞后性,使得本文算法仅适用于GNSS数据的后处理。但若对格网化的垂直剖面函数系数在时域建模,或者采用ECMWF的预测数据,可望实现本文算法在实时导航中的应用。此外,ECMWF在2016年已经开始发布最新的再分析资料(ERA5),目前其数据资料已涵盖1950年至今。作为ERA-Interim的替代产品,ERA5的显著优势是具有更高的时空分辨率,若采用ERA5再分析资料进行投影延拓,有望进一步提高本文算法的精度。
| [1] |
Dai L W. Augmentation of GPS with GLONASS and Pseudolite Signals for Carrier Phase Based Kinematic Positioning[D]. University of New South Wales, 2002
(  0) 0) |
| [2] |
邱蕾, 罗和平, 王泽民. GPS网络RTK流动站的对流层内插改正分析[J]. 测绘工程, 2011, 20(5): 70-73 (Qiu Lei, Luo Heping, Wang Zemin. The Analysis of Tropospheric Delay Model for GPS Net RTK[J]. Engineering of Surveying and Mapping, 2011, 20(5): 70-73 DOI:10.3969/j.issn.1006-7949.2011.05.019)
(  0) 0) |
| [3] |
张小红, 朱锋, 李盼, 等. 区域CORS网络增强PPP天顶对流层延迟内插建模[J]. 武汉大学学报:信息科学版, 2013, 38(6): 679-683 (Zhang Xiaohong, Zhu Feng, Li Pan, et al. Zenith Troposphere Delay Interpolation Model for Regional CORS Network Augmented PPP[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6): 679-683)
(  0) 0) |
| [4] |
Zheng Y, Feng Y M. Interpolating Residual Zenith Tropospheric Delays for Improved Regional Area Differential GPS Positioning[C]. ION GPS-2005, Long Beach, 2005
(  0) 0) |
| [5] |
王潜心, 许国昌, 陈正阳. 利用区域GPS网进行高海拔流动站的对流层延迟量内插[J]. 武汉大学学报:信息科学版, 2010, 35(12): 1 405-1 408 (Wang Qianxin, Xu Guochang, Chen Zhengyang. Interpolation Method of Tropospheric Delay of High Altitude Rover Based on Regional GPS Network[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1 405-1 408)
(  0) 0) |
| [6] |
王兴, 高井祥, 李增科, 等. EGNOS模型在对流层延迟插值方法改进中的应用[J]. 测绘科学技术学报, 2015, 32(4): 353-356 (Wang Xing, Gao Jingxiang, Li Zengke, et al. The Improved Interpolation Method of Tropospheric Delay Based on ENGOS Model[J]. Journal of Geomatics Science and Technology, 2015, 32(4): 353-356 DOI:10.3969/j.issn.1673-6338.2015.04.006)
(  0) 0) |
| [7] |
陈猛, 陈俊平, 胡丛玮.气象数值模型应用于GNSS精密单点定位[C].第七届中国卫星导航学术年会, 长沙, 2016 (Chen Meng, Chen Junping, Hu Congwei. Numerical Weather Models Applied in GNSS Precise Point Positioning[C]. The 7th China Satellite Navigation Conference, Changsha, 2016)
(  0) 0) |
| [8] |
陈钦明, 宋淑丽, 朱文耀.全球对流层延迟改正模型(SHAO-G)的初步建立[C].第二届中国卫星导航学术年会, 上海, 2011 (Chen Qinming, Song Shuli, Zhu Wenyao. Preliminary Establishment of the Global Model(SHAO-G) for the Zenith Tropospheric Delay[C]. The 2th China Satellite Navigation Conference, Shanghai, 2011)
(  0) 0) |
| [9] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2 218-2 227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2 218-2 227)
(  0) 0) |
| [10] |
赵静旸, 宋淑丽, 陈钦明, 等. 基于垂直剖面函数式的全球对流层天顶延迟模型的建立[J]. 地球物理学报, 2014, 57(10): 3 140-3 153 (Zhao Jingyang, Song Shuli, Chen Qinming, et al. Establishment of a New Global Model for Zenith Tropospheric Delay Based on Functional Expression for Its Vertical Profile[J]. Chinese Journal of Geophysics, 2014, 57(10): 3 140-3 153)
(  0) 0) |
| [11] |
陈猛.对流层模型上海地区适用性评估分析[D].上海: 同济大学, 2016 (Chen Meng. Performance Evaluation of Troposphere Models Application in Shanghai[D]. Shanghai: Tongji University, 2016)
(  0) 0) |
| [12] |
盛裴轩, 毛节泰, 李建国, 等. 大气物理学[M]. 北京: 北京大学出版社, 2003 (Sheng Peixuan, Mao Jietai, Li Jianguo, et al. Atmospheric Physics[M]. Beijing: Peking University Press, 2003)
(  0) 0) |
| [13] |
Hu Y F, Yao Y B. An Accurate Height Reduction Model for Zenith Tropospheric Delay Correction Using ECMWF Data[C]. The 8th China Satellite Navigation Conference, Shanghai, 2017)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


