对流层延迟作为一种重要的大气参数,是许多对地观测技术的重要误差源之一,国内外学者[1-7]在对流层延迟模型、对流层延迟估算方法和精度方面进行了大量研究。ERA-Interim数据时间分辨率较低,不能很好地反映天顶对流层延迟的日变化规律[8]。第五代再分析资料ERA5的时间和空间分辨率在ERA-Interim基础上有很大提升,但目前利用ERA5估计天顶对流层延迟精度方面研究较少。本文在利用再分析资料ERA5计算测站天顶对流层延迟的基础上,利用陆态网提供的2017年全年26个GNSS测站计算的ZTD对ERA5资料计算的天顶对流层延迟进行精度评估,为更好地使用ERA5资料提供参考。
1 基于ERA5再分析资料计算天顶对流层延迟的方法ERA5再分析资料不能直接提供天顶对流层延迟,且再分析资料的最高层距离地面高度为47 km左右,因此本文使用积分方式计算再分析资料高度范围内的对流层延迟ZTD1,使用Saastamoinen模型计算顶层以上部分的对流层延迟ZTD2,两者之和即为总的天顶对流层延迟[6]。
| $ \begin{array}{*{20}{c}} {Z{\rm{T}}{{\rm{D}}_1} = {{10}^{ - 6}}\int N {\rm{d}}s = }\\ {{{10}^{ - 6}}\sum\limits_i^{n - 1} {\left( {{N_i} + {N_{i + 1}}} \right)} \times \left( {{h_{i + 1}} - {h_i}} \right)/2} \end{array} $ | (1) |
| $ \begin{array}{l} {\rm{ZT}}{{\rm{D}}_2} = 0.0022793 \times \\ \left[ {\frac{{{P_1} + \left( {0.05 + \frac{{1255}}{T}} \right){e_1}}}{{f(\varphi , H)}}} \right] \end{array} $ | (2) |
其中,
| $ N = {k_1}(P - e)/T + {k_2} \times e/T + {k_3} \times e/{T^2} $ | (3) |
| $ e = q \times P/0.622 $ | (4) |
| $ \begin{array}{l} f(\varphi , h) = \\ 1 - 0.00266\cos (2\varphi ) - 2.8 \times {10^{ - 7}}H \end{array} $ | (5) |
式中,n为GNSS测站以上再分析资料中包含的总层数,k1=77.604 K/hPa,k2=64.79 K/hPa,k3=3 754 630 K2/hPa,P为气压(单位hPa),e为水汽分压(单位hPa),q为比湿(单位kg/kg),T为温度(单位K),φ为GNSS测站对应的纬度(单位°),P1、e1和H分别为站点上空在再分析资料顶层时对应的气压、水汽分压及距离海平面的高程(单位m)。
GNSS测站一般不与再分析资料的格网点重合,且站点高程也与资料模型层高程不相等,因此需要通过内插方式获取公式(1)~(4)中所需的气象参数,内插之前必须进行高程参考系统的统一。再分析资料采用的高程参考系统为位势高,而GNSS基准站的高程系统为大地高,在内插GNSS测站位置的气象数据之前必须将测站大地高转为位势高。利用EGM2008模型先将大地高转为正高,由于正高和位势高之间差异非常小,本文使用正高来近似代替位势高[9-10]。完成高程转换后,余下步骤为:
1) 根据站点近似坐标寻找距离站点最近的4个格网点,然后线性内插出4个格网点在高程等于GNSS测站高程时对应的气象参数;
2) 使用二维线性内插方法将步骤1)中的4个格网点的气象参数内插到GNSS测站位置;
3) 使用二维线性内插方法分别内插出GNSS测站以上各层经纬度坐标与站点坐标一致、高度等于各层高度时的气象参数;
4) 使用公式(1)和(2)分别计算ZTD1和ZTD2,并相加。
2 基于ERA5再分析资料计算天顶对流层延迟的精度评估本文选取26个测站在2017年全年的GNSS观测值及GPS和GLONASS系统观测数据,用来评价再分析资料ERA5计算对流层延迟的精度,GNSS测站位置如图 1所示。利用GAMIT/GLOBK软件解算天顶对流层延迟,对流层投影函数为GMF[11],卫星截止高度角为10°,每隔1 h估计一次天顶对流层延迟[10]。再分析资料ERA5选择水平方向格网分辨率为0.25°×0.25°、垂直方向上包含37层压力层、时间分辨率为1 h的数据,同时与使用水平方向格网分辨率为0.25°×0.25°、垂直方向上包含37层压力层、时间分辨率为6 h的ERA-Interim资料进行对比分析。考虑到GNSS天顶对流层延迟、ERA5和ERA-Interim的分辨率分别为1 h、1 h和6 h,全部GNSS对流层延迟数据可用来与ERA5进行比较,而在比较GNSS与ERA-Interim时只选用与ERA-Interim相同时刻的GNSS天顶对流层延迟数据。
|
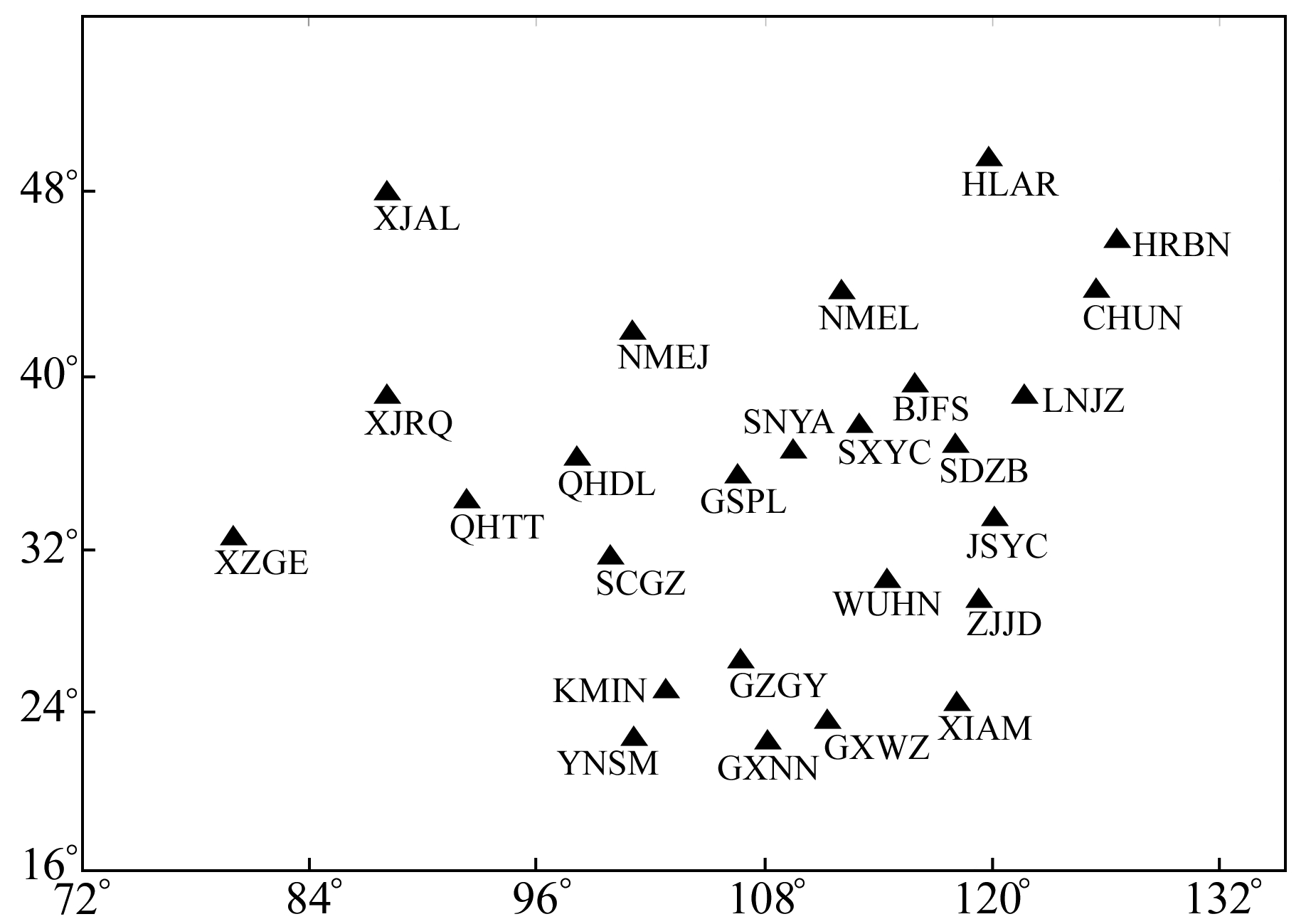
图 1 GNSS测站分布 Fig. 1 Distribution of selected GNSS stations |
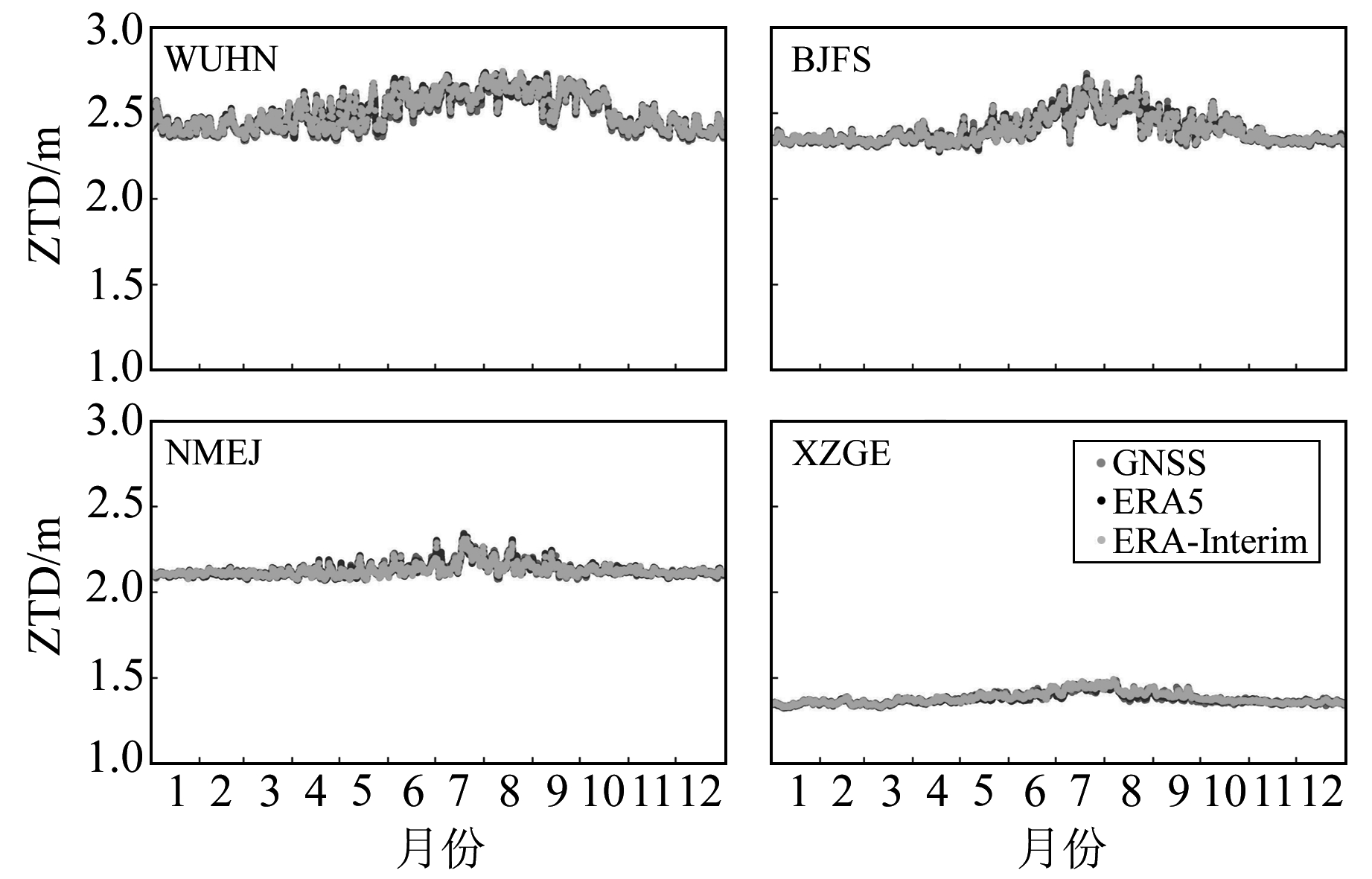
选择WUHN、BJFS、NMEJ、XZGE 4个测站,分析GNSS、ERA5和ERA-Interim计算的天顶对流层延迟全年变化。从图 1可以看出,这4个测站分别位于中国南方地区、北方地区、西北地区以及青藏高原,代表着各地不同的气候特征。图 2为上述4个测站分别使用ERA5、ERA-Interim及GNSS这3种方法计算的天顶对流层延迟的全年变化趋势。可以看出,对流层延迟呈现先上升后下降的变化趋势,3种方法获得的结果具有非常好的一致性。4个测站的对流层延迟变化范围都在1~3 m之间,位于海拔较低区域的WUHN和BJFS站的天顶对流层延迟明显大于另外两个测站,特别是海拔最高的XZGE站,全年的天顶对流层延迟比WUHN站小1 m左右。以GNSS计算的天顶对流层延迟作为参考,表 1(单位mm)为上述4个测站ERA5和ERA-Interim在每个月的RMS值。从表中可以看出,4个测站的RMS呈现先增大后减小的趋势,且在5~9月的偏差明显大于其他月份。该时段正处于中国的雨季,因此可能与大气中水汽含量增多和大气对流强烈而引起再分析资料误差增大有关。
|
图 2 WUHN、BJFS、NMEJ、XZGE站2017年全年对流层延迟变化趋势 Fig. 2 Zenith tropospheric delay derived from GNSS, ERA5 and ERA-Interim at WUHN, BJFS, NMEJ and XZGE stations in 2017 |
|
|
表 1 不同月份ERA5及ERA-Interim计算的对流层延迟偏差的RMS值统计 Tab. 1 Monthly RMS statistics of zenith tropospheric delay derived from ERA5 and ERA-Interim |
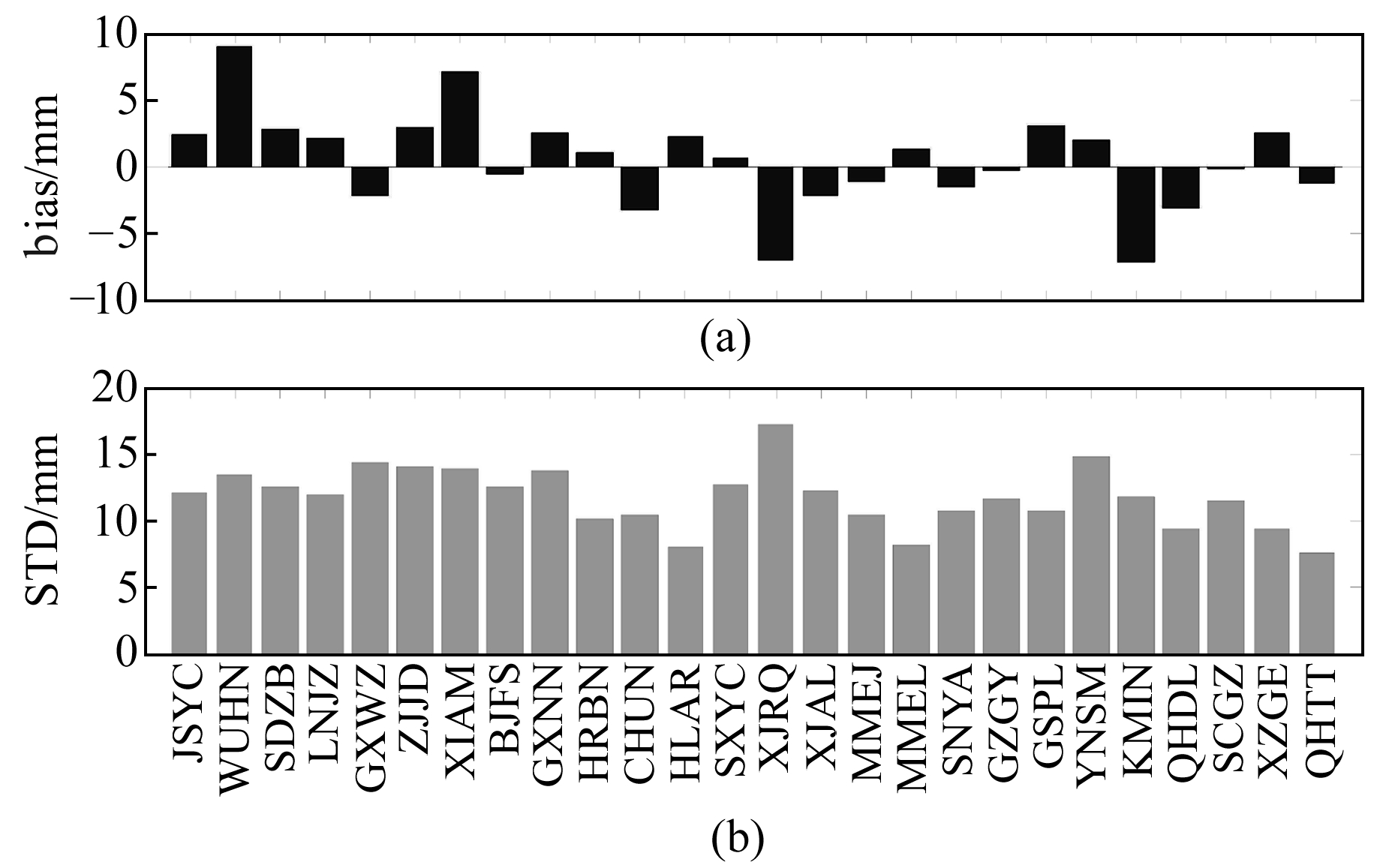
图 3为按高程由低到高顺序排列的各个测站全年ERA-Interim对流层延迟相较于GNSS的平均偏差(bias)和标准差(STD)。由图可见,偏差和STD值随高程增加并没有呈现出明显的函数关系,表明两者的误差并不是由高程变化引起的。同时,所有测站的平均偏差都在±10 mm以内,STD值都在20 mm以内。
|
图 3 所有测站ERA-Interim资料计算的对流层延迟平均偏差和STD值统计 Fig. 3 Mean bias and STD of ERA-Interim ZTD at different stations with height sorted from low to high |
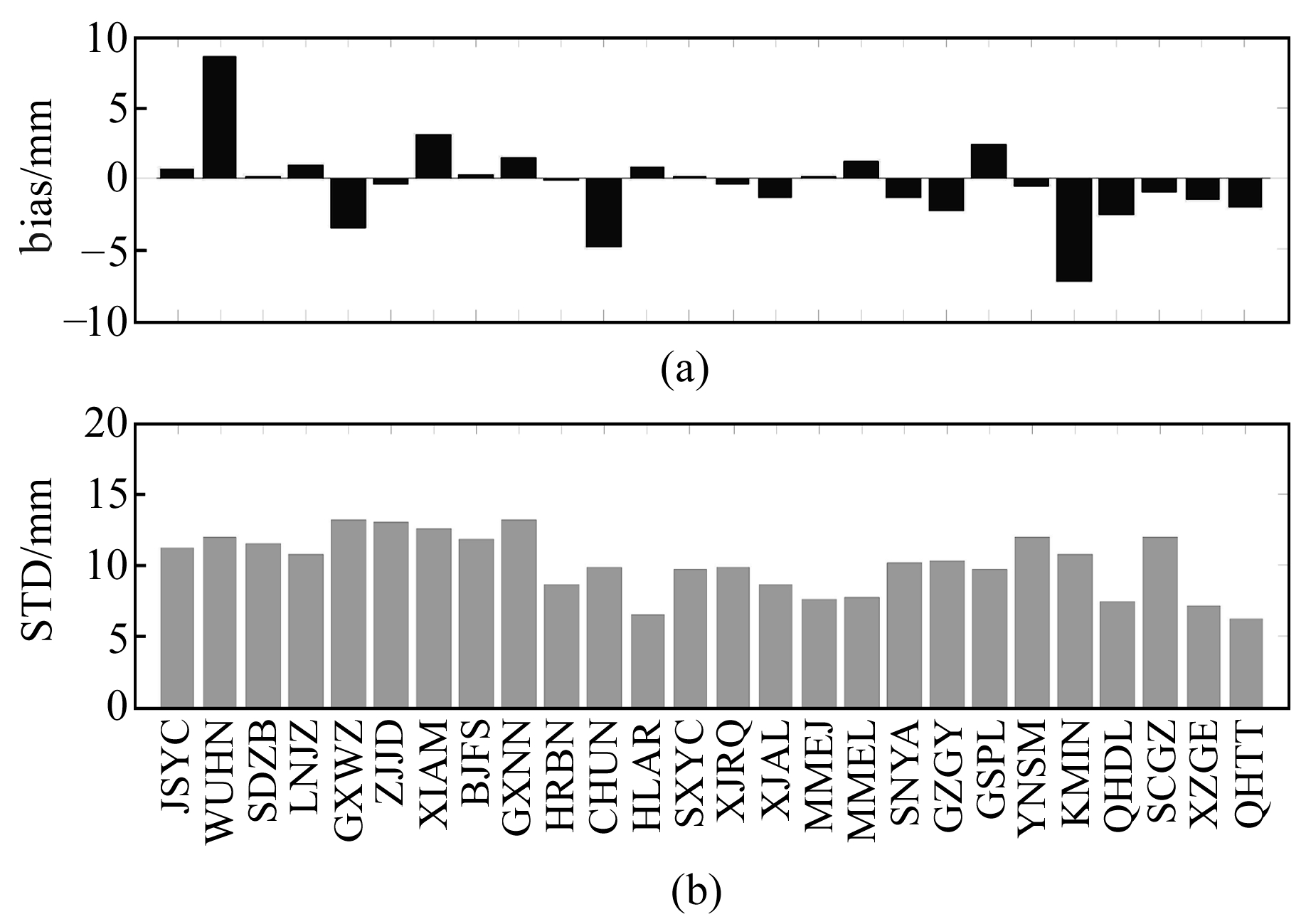
图 4为按高程由低到高依次排列的所有测站全年ERA5资料计算的天顶对流层延迟相对于GNSS的平均偏差和STD值变化情况。由图可见,平均偏差和STD值随高程的变化趋势与ERA-Interim类似,与高程没有明显的函数关系。ERA5资料与ERA-Interim资料的估算精度处于相同的范围,所有测站的平均偏差都在±10 mm以内,STD值都在20 mm以内。表 2(单位mm)为所有测站两种资料计算的天顶对流层延迟相对于GNSS的精度,由表可见,两种资料计算结果与GNSS之间的偏差非常接近于0,表明其与GNSS估计的对流层延迟都不存在明显的系统偏差。ERA5的偏差和RMS最大值都比ERA-Interim要小,ERA5的RMS平均值比ERA-Interim小约14%。
|
图 4 所有测站ERA5再分析资料计算的对流层延迟平均偏差和STD值统计 Fig. 4 Mean bias and STD of ERA5 ZTD at different stations with height sorted from low to high |
|
|
表 2 利用ERA-Interim、ERA5计算天顶对流层延迟的平均偏差和RMS值统计 Tab. 2 Totally mean bias and RMS statistics of ZTD derived from ERA-Interim and ERA5 |
为更好地分析ERA-Interim和ERA5资料计算的天顶对流层延迟在中国不同区域的精度情况,图 5为上述两种再分析资料估计对流层延迟的RMS值在地域上的分布情况,每个圆点代表一个GNSS测站。由图可见,这两种再分析资料在南方地区的RMS值要明显大于其他区域,可能与该地区海拔较低、气候湿润、降水丰沛等因素有关。总体来看,ERA5估计对流层延迟的精度要明显优于ERA-Interim。

|
图 5 由ERA-Interim和ERA5计算的天顶对流层延迟的RMS值分布 Fig. 5 RMS distribution of ZTD derived from ERA5 and ERA-Interim with respect to GNSS-derived ZTD |
1) 由ERA5计算的对流层延迟的平均偏差和RMS比ERA-Interim结果要小,并且两者的平均偏差非常接近于0,表明ERA5的精度比ERA-Interim要高。同时,用再分析资料计算的对流层延迟与GNSS计算的天顶对流层延迟之间不存在明显的系统偏差。
2) ERA5和ERA-Interim计算的天顶对流层延迟精度随测站高程的上升没有明显变化,但在不同季节和不同区域有着明显差异,夏季的误差要大于其他季节的误差,南方地区两种再分析资料的RMS值明显高于其他区域。
| [1] |
Böhm J, Möller G, Schindelegger M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere(GPT2w)[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [2] |
Yao Y B, Xu C Q, Shi J B, et al. ITG: A New Global GNSS Tropospheric Correction Model[J]. Scientific Reports, 2015(5): 10 273
(  0) 0) |
| [3] |
Lu C X, Zus F, Ge M, et al. Tropospheric Delay Parameters from Numerical Weather Models for Multi-GNSS Precise Positioning[J]. Atmospheric Measurement Techniques, 2016, 9(12): 5 965-5 973 DOI:10.5194/amt-9-5965-2016
(  0) 0) |
| [4] |
Lu C X, Li X X, Zus F, et al. Improving Beidou Real-Time Precise Point Positioning with Numerical Weather Models[J]. Journal of Geodesy, 2017, 91(9): 1 019-1 029 DOI:10.1007/s00190-017-1005-2
(  0) 0) |
| [5] |
Andrei C O, Chen R Z. Assessment of Time-Series of Troposphere Zenith Delays Derived from the Global Data Assimilation System Numerical Weather Model[J]. GPS Solutions, 2009, 13(2): 109-117 DOI:10.1007/s10291-008-0104-1
(  0) 0) |
| [6] |
Chen Q M, Song S L, Heise S, et al. Assessment of ZTD Derived from ECMWF/NCEP Data with GPS ZTD over China[J]. GPS Solutions, 2011, 15(4): 415-425 DOI:10.1007/s10291-010-0200-x
(  0) 0) |
| [7] |
马志泉, 陈钦明, 高德政. 用中国地区ERA-Interim资料计算ZTD和ZWD的精度分析[J]. 大地测量与地球动力学, 2012, 32(2): 100-104 (Ma Zhiquan, Chen Qinming, Gao Dezheng. Study on Accuracy of ZTD and ZWD Calculated from ERA-Interim Data over China[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 100-104)
(  0) 0) |
| [8] |
黄瑾芳, 楼益栋, 张卫星, 等. 再分析资料计算中国区域对流层延迟精度[J]. 测绘科学, 2018, 43(5): 13-17 (Huang Jinfang, Lou Yidong, Zhang Weixing, et al. The Assessment of ZTD Calculated from Reanalysis over China[J]. Science of Surveying and Mapping, 2018, 43(5): 13-17)
(  0) 0) |
| [9] |
章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 5-11 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 5-11)
(  0) 0) |
| [10] |
Jiang P, Ye S R, Chen D Z, et al. Retrieving Precipitable Water Vapor Data Using GPS Zenith Delays and Global Reanalysis Data in China[J]. Remote Sensing, 2016, 8(5): 389-409 DOI:10.3390/rs8050389
(  0) 0) |
| [11] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33: L07304
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40


