2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉市徐东大街340号, 430077;
3. 中国科学院大学, 北京市玉泉路甲19号, 100049
近年来,随着美国GPS、中国BDS、欧盟Galileo等系统的日趋完善,多系统多频率组合相对定位成为研究的热点[1-2],尤其在2012-12北斗系统开始为亚太及周边用户提供区域服务以及在2016-12 Galileo开始提供初始服务以来,基于GPS/BDS/Galileo数据的相对定位成为研究的热点。
已有研究表明,联合多系统数据可有效增加可见卫星数目,提高模糊度固定成功率和定位精度,其改善效果在高截止高度角情况下更加明显,从而在一些特定的环境(如城市中心等卫星遮挡比较严重的地区),多系统组合定位会比单系统定位更有优势[3-5]。为了进一步利用多系统联合相对定位中的有效信息提高定位性能,Odijk、张小红等[6-8]分别对GPS/Galileo、BDS/Galileo双系统间的重叠频率观测数据的接收机系统间偏差特性进行分析,结果表明,接收机系统间偏差具有长期的稳定性,而且使用双系统混合双差较单系统能有效提高定位的性能。而对不同频率的数据联合处理问题,楼益栋、Gao等[9-12]对GPS/BDS联合定位情形开展研究,提出GPS/BDS混合双差模型,分析结果表明,混合双差模型在高截止高度角情形下可有效提高模糊度首次固定的时间和成功率。
目前,由于GLONASS采用频分多址的信号体制,与其他系统采用的码分多址不同,所以很少有GLONASS与其他系统组合的混合差分定位研究,而对于GPS/BDS或BDS/Galileo双系统重叠频率上针对混合差分相对定位的研究较多。另外,对三系统混合双差的相对定位研究较少。对三系统组合混合差分定位的研究不仅能体现全球GNSS系统的互操作性,而且在高截止高度角的情况下,三系统组合能增加可见卫星数目,增加观测数量,提高定位性能。本文对单/双频GPS L1/L2-BDS B1/B2-Galileo E1/E5a混合双差相对定位模型算法进行研究,并选择短基线数据开展实验,对不同系统、频率及高度角情形下的模糊度首次固定速度和定位精度进行对比分析,可为多星座GNSS系统间的有效融合提供一定的参考。
1 混合双差相对定位数学模型在短基线相对定位中,通常通过星间/站间差分来消除卫星/接收机钟差、电离层延迟、对流层延迟等误差的影响。假设选择一颗GPS卫星作为参考星,以GPS/BDS/Galileo卫星为流动星,其相位/伪距观测方程可表示为:
| $ \left\{ \begin{array}{l} \varphi _{12, j}^{{1_{\rm{G}}}{\rm{s}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{s}}} + {\lambda _{{\varepsilon _j}}}N_{12, j}^{{1_{\rm{G}}}{\rm{s}}} + \varepsilon _{12, j}^{{1_{\rm{G}}}{\rm{s}}}\\ \varphi _{12, j}^{{1_{\rm{G}}}{\rm{k}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{k}}} + {\lambda _{{c_j}}}N_{12, {c_j}}^{\rm{k}} - {\lambda _{{g_j}}}N_{12 \cdot {\varepsilon _j}}^{{1_{\rm{G}}}} + \delta _{12}^{{\rm{GC}}} + \varepsilon _{12}^{{1_{\rm{G}}}{\rm{k}}}\\ \varphi _{12, j}^{{1_{\rm{G}}}{\rm{q}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{q}}} + {\lambda _{{e_j}}}N_{12, {e_j}}^{\rm{q}} - {\lambda _{{g_j}}}N_{12, {g_j}}^{{1_{\rm{G}}}} + \delta _{12}^{{\rm{GE}}} + \varepsilon _{12}^{{1_{\rm{G}}}{\rm{q}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{s}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{s}}} + e_{12, j}^{{1_{\rm{G}}}{\rm{s}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{k}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{k}}} + d_{12}^{{\rm{GC}}} + e_{12}^{{1_{\rm{G}}}{\rm{k}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{q}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{q}}} + d_{12}^{{\rm{GE}}} + e_{12}^{{1_{\rm{G}}}{\rm{q}}} \end{array} \right. $ | (1) |
式中,上标s、k、q分别表示GPS、BDS和Galileo卫星,上标G、C、E分别表示GPS、BDS、Galileo系统,δ12GC、d12GC和δ12GE、d12GE分别为BDS、Galileo相对于GPS的接收机相位、伪距系统间偏差,λj为对应信号频率的波长,φ、P分别表示相位和伪距观测值,ρ表示卫星到测站之间的几何距离,N为整周模糊度,ε、e分别表示相位、伪距观测噪声。
由于频率的不一致以及接收机端的硬件延迟的影响,GPS/BDS和GPS/Galileo系统间的载波相位双差观测不能形成具有整数特性的双差模糊度。这里将进行参数重组,引入BDS参考星和Galileo参考星,则BDS、Galileo的模糊度与系统间偏差项可以表示为:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\lambda _{{c_j}}}N_{12, {c_j}}^{\rm{k}} - {\lambda _{{g_j}}}N_{12, {g_j}}^{{1_{\rm{G}}}} + \delta _{12}^{{\rm{GC}}} = \left( {{\lambda _{{c_j}}}N_{12, {c_j}}^{\rm{k}} - } \right.}\\ {\left. {\quad {\lambda _{{c_j}}}N_{12 \cdot {c_j}}^{{1_{\rm{C}}}}} \right) + \left( {{\lambda _{{c_j}}}N_{12, {c_j}}^{{1_{\rm{C}}}} - {\lambda _{{g_j}}}N_{12, {g_j}}^1 + \delta _{12}^{{\rm{GC}}}} \right) = }\\ {{\lambda _{{c_j}}}N_{12, {c_j}}^{{1_{\rm{C}}}{\rm{k}}} + {\mathop{\rm DISB}\nolimits} _{L, j}^{{\rm{GC}}}} \end{array}\\ {\lambda _{{e_j}}}N_{12, {e_j}}^{\rm{q}} - {\lambda _{{\varepsilon _j}}}N_{12 \cdot {g_j}}^{{1_{\rm{G}}}} + \delta _{12}^{{\rm{GE}}} = \left( {{\lambda _{{e_j}}}N_{12, {e_j}}^{\rm{q}} - } \right.\\ \begin{array}{*{20}{l}} {\left. {{\lambda _{{e_j}}}N_{12, {e_j}}^{{1_{\rm{E}}}}} \right) + \left( {{\lambda _{{e_j}}}N_{12, {e_j}}^{1{\rm{F}}} - {\lambda _{{E_j}}}N_{12, {g_j}}^{{1_{\rm{G}}}} + \delta _{12}^{{\rm{GE}}}} \right) = }\\ {{\lambda _{{e_j}}}N_{12, {e_j}}^{{1_{\rm{E}}}{\rm{q}}} + {\rm{D}}{\mathop{\rm ISB}\nolimits} _{L, j}^{{\rm{GE}}}} \end{array} \end{array} \right. $ | (2) |
式中,
| $ \left\{ \begin{array}{l} \varphi _{12, j}^{{1_{\rm{G}}}{\rm{s}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{s}}} + {\lambda _j}N_{12, j}^{{1_{\rm{G}}}{\rm{s}}} + \varepsilon _{12, j}^{{1_{\rm{G}}}{\rm{s}}}\\ \varphi _{12, j}^{{1_{\rm{G}}}{\rm{k}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{k}}} + {\lambda _{{c_j}}}N_{12, {c_j}}^{{1_{\rm{C}}}{\rm{k}}} + {\rm{DISB}}_{L, j}^{{\rm{GC}}} + \varepsilon _{12}^{{1_{\rm{G}}}{\rm{k}}}\\ \varphi _{12, j}^{{1_{\rm{G}}}{\rm{q}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{q}}} + {\lambda _{{e_j}}}N_{12, {e_j}}^{{1_{\rm{E}}}{\rm{q}}} + {\rm{DISB}}_{L, j}^{{\rm{GE}}} + \varepsilon _{12}^{{1_{\rm{G}}}{\rm{q}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{s}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{s}}} + e_{12, j}^{{1_{\rm{G}}}{\rm{s}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{k}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{k}}} + {\rm{DISB}}_{P, j}^{{\rm{GC}}} + e_{12}^{{1_{\rm{G}}}{\rm{k}}}\\ P_{12, j}^{{1_{\rm{G}}}{\rm{q}}} = \rho _{12, j}^{{1_{\rm{G}}}{\rm{q}}} + {\rm{DISB}}_{P, j}^{{\rm{GE}}} + e_{12}^{{1_{\rm{G}}}{\rm{q}}} \end{array} \right. $ | (3) |
式中,DISBL, jGC、DISBP, jGC、DISBL, jGE、DISBP, jGE分别为参数重组后GPS/BDS、GPS/Galileo的相位、伪距接收机系统间偏差,其中j表示频率。
在数据处理中随机模型采用普通高度角模型:
| $ \sigma=\sigma_{0}\left(1+\alpha \cos ^{2} E\right) $ | (4) |
式中,σ表示观测值标准差,σ0表示天顶方向非差观测值的标准差,E表示卫星高度角,系数α取1.5。
2 算例分析 2.1 实验数据及处理策略选取澳大利亚Curtin大学两条短基线(CUT0-CUTA、CUT0-CUTB)2017-04-15~04-19共5 d的观测数据进行分析,数据采样间隔为30 s,解算模式使用GPS单系统、GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差和GPS/BDS/Galileo混合双差,解算时采用高度角定权方法,使用广播星历计算卫星位置。
数据处理中采用序贯最小二乘进行参数估计,在每个历元先计算模糊度浮点解,然后采用最小二乘模糊度降相关平差法(LAMBDA)尝试模糊度固定[12],并根据Ratio检验判断模糊度固定是否成功,其限差设置为3。若固定成功,将固定解作为虚拟观测方程列入参数估计中,得到基线固定解;否则,直接输出浮点解。
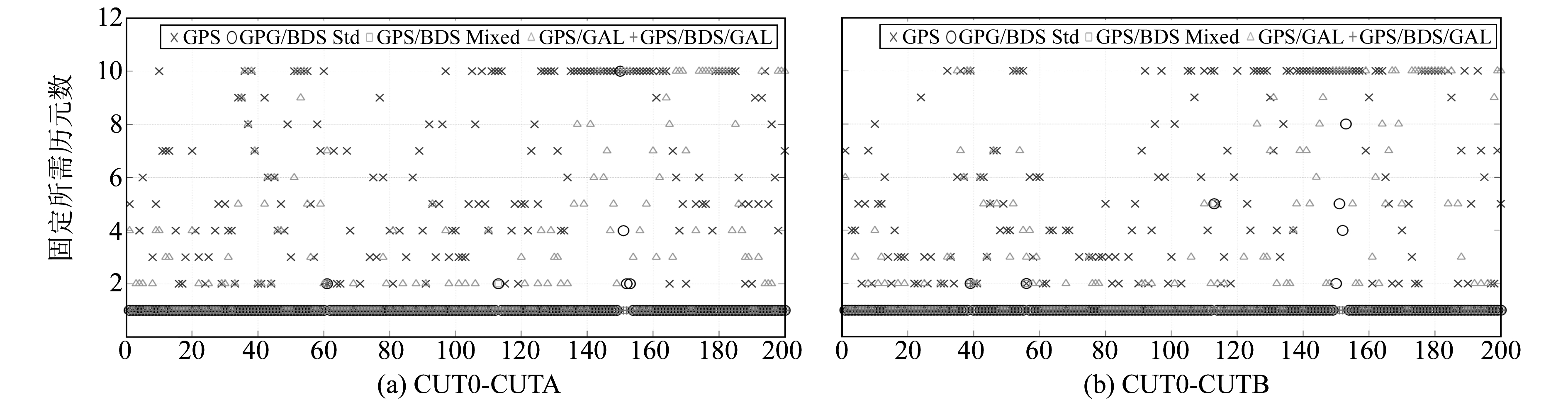
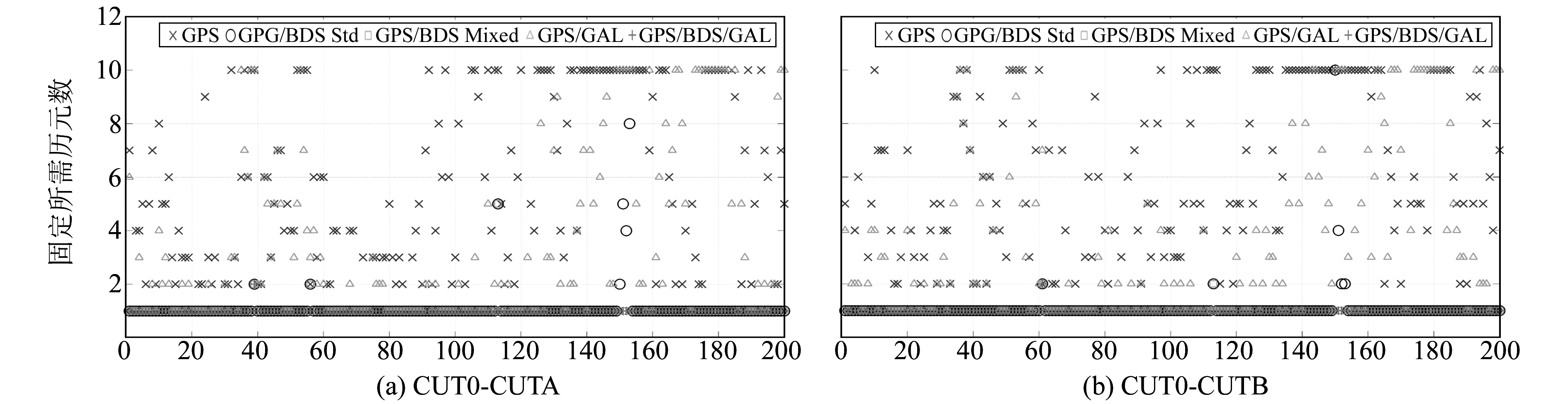
2.2 模糊度首次固定时间分析为了分析不同情形下模糊度首次固定所需的历元数目,将数据以5 min作为一个时段进行处理。为了清晰地显示结果,图 1~4为短基线CUT0-CUTA、CUT0-CUTB的5 d数据(一共1 440个时段)中前200个时段在不同解算模式下每个时间段实现模糊度固定所需历元数目的时间序列。同时为了节约篇幅,这里仅给出截止高度角为15°、25°的统计结果。
|
图 1 CUT0-CUTA、CUT0-CUTB基线单频截止高度角为15°时模糊度固定所需历元数的时间序列 Fig. 1 Time series of epochs required for fixed ambiguity of CUT0-CUTA, CUT0-CUTB baseline single-frequency at 15°cut-off angle |
|
图 2 CUT0-CUTA、CUT0-CUTB基线单频截止高度角为25°时模糊度固定所需历元数的时间序列 Fig. 2 Time series of epochs required for fixed ambiguity of CUT0-CUTA, CUT0-CUTB baseline single-frequency at 25°cut-off angle |

|
图 3 CUT0-CUTA、CUT0-CUTB基线双频截止高度角为15°时模糊度固定所需历元数的时间序列 Fig. 3 Time series of epochs required for fixed ambiguity of CUT0-CUTA, CUT0-CUTB baseline dual-frequency at 15°cut-off angle |

|
图 4 CUT0-CUTA、CUT0-CUTB基线双频截止高度角为25°时模糊度固定所需历元数的时间序列 Fig. 4 Time series of epochs required for fixed ambiguity of CUT0-CUTA, CUT0-CUTB baseline dual-frequency at 25°cut-off angle |
单频情况下,由图 1、图 2可以看出,两条基线的情况类似,随着截止高度角从15°增大至25°,两条基线GPS单系统模糊度首次固定所需历元数目随着截止高度角的升高而增加,GPS/Galileo较GPS单系统在所需历元数目上增长偏慢,但仍有显著增加;GPS/BDS标准双差随着高度角上升个别时间段所需历元数目会增加,但大部分时间段只需1个历元就能固定;GPS/BDS混合双差和GPS/BDS/Galileo混合双差情形下都只需要1个或2个历元即可实现模糊度固定,并且整个时间范围内较为稳定。
由图 3和图 4可以看出,相比之下,采用双频观测值时,由于增加了有效信息,在所有解算模式下模糊度首次固定所需历元数目均进一步减少;两条基线随着高度角升高,GPS单系统模糊度固定所需历元数目会随之增加,GPS/Galileo虽然增长不明显但仍有增加趋势,而GPS/BDS标准双差、GPS/BDS混合双差、GPS/BDS/Galileo在每个时间段上首次固定所需历元数依然只是1~2个。
处理所有观测数据,表 1统计了两条基线单/双频情形下,不同高度角和解算模式下模糊度首次固定所需历元数的平均值。由表 1可知,在单频情况下,截止高度角为5°、10°时,GPS单系统所需历元数的均值在1.92~2.67个,GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差、GPS/BDS/Galileo混合双差情形下所需历元数为1.00~1.35个。同时从表 1可以看出,当高度角分别为15°、20°、25°时,GPS单系统模糊度首次固定所需历元数的均值在3.65~6.39个,有不断增加的趋势;GPS/BDS标准双差在1.01~1.09个,也有微小增加的趋势;但是GPS/BDS混合双差和GPS/BDS/Galileo混合双差仍然保持在1.00~1.03个,较GPS单系统有大幅度的提升,较GPS/BDS标准双差也有微小的提升。另外,随着截止高度角上升,GPS/Galileo混合双差虽然比GPS/BDS标准双差、GPS/BDS混合双差或者GPS/BDS/Galileo混合双差固定所需历元数均值要多一些,但是较GPS单系统仍然有一定的提升。在双频情况下,从表 1可以看出,5种模式下模糊度首次固定所需历元数的均值整体较单频有所减少。截止高度角为5°、10°、15°时,GPS单系统模糊度首次固定所需历元数的均值在1.00~1.29个,其他模式下两条基线模糊度首次固定所需历元数的均值在1.00或1.01个;高度角上升至20°时,GPS单系统模糊度首次固定所需历元数的均值为2.12个,GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差以及GPS/BDS/Galileo平均1.00或1.05个历元就能固定;当高度角增加至25°时,GPS单系统平均需要3.45个历元才能固定,GPS/Galileo混合双差平均需要1.58个历元可以固定,而GPS/BDS标准双差、GPS/BDS混合双差以及GPS/BDS/Galileo混合双差较其他两种模式表现出更大的优势,平均仅需1.00个历元就能固定。
|
|
表 1 单、双频模糊度固定所需历元数均值的统计 Tab. 1 Single and dual-frequency statistics of epoch mean values required for fixed ambiguity |
为分析不同模式下的定位精度情况,连续处理所有观测数据,统计基线固定解精度。单/双频情形下的定位精度统计结果分别如表 2(单位mm)和表 3(单位mm)所示。
|
|
表 2 单频三维坐标固定解RMS统计 Tab. 2 Single-frequency statistics of fixed 3D coordinate RMS |
由表 2可见,在单频情况下,截止高度角为5°~15°时,在水平方向上,两条基线的5种解算模式的RMS均在4 mm以内,其中GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差、GPS/BDS/Galileo混合双差的精度分别比GPS单系统的精度提升了约25%、25%、15%、31%;在高程方向上,GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差和GPS/BDS/Galileo混合双差较GPS单系统的精度提高了约19%、19%、17%、26%。此外,GPS/BDS标准双差和其他组合系统混合双差无论在水平方向还是高程方向上精度均相当。当高度角增加到20°、25°时,在水平方向上,GPS单系统解算两条基线的RMS在约7 mm以内,GPS/Galileo混合双差解算的水平RMS在约3 mm以内,但相比之下,所有基线在GPS/BDS标准双差、GPS/BDS混合双差、GPS/BDS/Galileo混合双差下均保持在约2 mm以内,此时GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差、GPS/BDS/Galileo混合双差较GPS单系统精度分别提升了45%、45%、33%、50%。可以看出,组合系统精度提升效果显著,在高程方向上,GPS单系统RMS最大达到约1.1 cm,两条基线GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差以及GPS/BDS/Galileo混合双差较GPS单系统精度分别提升了32%、33%、23%、38%。同样,在此高度角情形下,其他组合系统混合双差较GPS/BDS标准双差无论在水平方向还是高程方向上的精度都大致相同。
表 3显示,相比之下,双频较单频提高了基线向量的精度,截止高度角为5°~20°时,在水平方向上,GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差、GPS/BDS/Galileo混合双差的精度较GPS单系统的精度分别提升了25%、25%、15%、33%,两系统或者三系统组合的精度较单GPS系统的精度有所提高,但是差距仅在mm或者亚mm级别;在高程方向上,随着截止高度角的增加,两条基线GPS单系统和GPS/Galileo的RMS呈下降趋势,GPS单系统最大达到8.8 mm,其他4种解算模式较GPS单系统的精度分别提高了23%、23%、17%、30%。当截止高度角上升至25°时,在水平方向上,多系统组合的精度较GPS单系统的精度分别提升61%、61%、47%、62%;在高程方向上,分别提高了37%、37%、26%、44%。另外,其他混合双差模式的精度较GPS/BDS标准双差的精度提升不是很明显,但总体可以看出在较高高度角情形下,多系统组合表现出更大的优势。
|
|
表 3 双频三维坐标固定解RMS统计 Tab. 3 Dual-frequency statistics of fixed 3D coordinate RMS |
本文对单/双频多系统联合相对定位性能展开研究,推导了GPS/BDS/Galileo混合双差相对定位模型,并选取短基线单/双频观测数据,设置不同高度角来模拟在卫星观测数不同的环境下进行实验,对比分析单GPS系统、GPS/BDS标准双差和多系统混合双差在模糊度首次固定时间以及基线定位精度方面的差异。
从分析结果可知,在模糊度首次固定时间方面,使用混合双差联合多系统、多频率数据可以有效加速模糊度固定,这一特点在高截止高度角时更加显著,例如当高度角达到25°时,采用GPS/BDS/Galileo混合双差时,单/双频情况下平均1~2个历元就能实现模糊度的首次固定,从而相比于单系统有着较大的优势。GPS/BDS混合双差也会随着高度角上升体现出模糊度固定速度快的优势,较GPS/BDS标准双差也有一定提升。在定位精度方面,低截止高度角时,由于GPS单系统和多系统组合可观测卫星数量充足,单/双频多系统组合较GPS单系统基线精度有一定的提升,但差别仅在mm级,效果不是很明显;在高截止高度角(25°)时,无论是单、双频,GPS/BDS/Galileo混合双差、GPS/BDS标准双差、GPS/BDS混合双差、GPS/Galileo混合双差分别较GPS单系统在水平和高程方向的精度都有明显提升,但是其他组合模式的混合双差与GPS/BDS标准双差精度相当,提升效果不明显。
| [1] |
杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253-259 (Yang Yuanxi, Lu Mingquan, Han Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253-259)
(  0) 0) |
| [2] |
李建文, 李作虎, 郝金明, 等. GNSS的兼容与互操作初步研究[J]. 测绘科学技术学报, 2009, 26(3): 177-180 (Li Jianwen, Li Zuohu, Hao Jinming, et al. A Preliminary Study on Compatibility and Interoperability of GNSS[J]. Journal of Geomatics Science and Technology, 2009, 26(3): 177-180 DOI:10.3969/j.issn.1673-6338.2009.03.006)
(  0) 0) |
| [3] |
He H, Li J, Yang Y, et al. Performance Assessment of Single- and Dual-Frequency Beidou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403 DOI:10.1007/s10291-013-0339-3
(  0) 0) |
| [4] |
Deng C, Tang W, Liu J, et al. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/Beidou System[J]. GPS Solutions, 2014, 18(3): 375-386 DOI:10.1007/s10291-013-0337-5
(  0) 0) |
| [5] |
宋志勇, 高晓, 石强, 等. GPS/BDS/Galileo多模单频单历元RTK定位算法[J]. 测绘科学技术学报, 2016, 33(3): 226-235 (Song Zhiyong, Gao Xiao, Shi Qiang, et al. Instantaneous Single-Frequency RTK Positioning Using Combined GPS/BDS/GALILEO System[J]. Journal of Geomatics Science and Technology, 2016, 33(3): 226-235)
(  0) 0) |
| [6] |
Odijk D, Teunissen P J. Characterization of Between-Receiver GPS-Galileo Inter-System Biases and Their Effect on Mixed Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 521-533 DOI:10.1007/s10291-012-0298-0
(  0) 0) |
| [7] |
Paziewski J, Wielgosz P. Accounting for Galileo-GPS Inter-System Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81-93 DOI:10.1007/s00190-014-0763-3
(  0) 0) |
| [8] |
张小红, 吴明魁, 刘万科. Beidou B2/Galileo E5b短基线紧组合相对定位模型及性能评估[J]. 测绘学报, 2016, 45(增2): 1-11 (Zhang Xiaohong, Wu Mingkui, Liu Wanke. Model and Performance Analysis of Tightly Combined Beidou B2 and Galileo E5b Relative Positioning for Short Baseline[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 1-11)
(  0) 0) |
| [9] |
楼益栋, 龚晓鹏, 辜声峰, 等. GPS/BDS混合双差RTK定位方法及结果分析[J]. 大地测量与地球动力学, 2016, 36(1): 1-5 (Lou Yidong, Gong Xiaopeng, Gu Shengfeng, et al. An Algorithm and Results Analysis for GPS/BDS Inter-System Mix Double-Difference RTK[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 1-5)
(  0) 0) |
| [10] |
隋心, 邹鑫慈, 徐爱功, 等. GPS/BDS接收机端系统偏差实时估计方法[J]. 测绘科学, 2016, 41(12): 106-109 (Sui Xin, Zou Xinci, Xu Aigong, et al. A Real-Time Estimation Algorithm for the GPS/BDS Inter-System Biases at the Receiver End[J]. Science of Surveying and Mapping, 2016, 41(12): 106-109)
(  0) 0) |
| [11] |
Gao W, Meng X, Gao C, et al. Combined GPS and BDS for Single-Frequency Continuous RTK Positioning through Real-Time Estimation of Differential Inter-System Biases[J]. GPS Solutions, 2018, 22(1): 20 DOI:10.1007/s10291-017-0687-5
(  0) 0) |
| [12] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2020, Vol. 40
2020, Vol. 40

