2. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079
在许多应用中,例如精准农业自动转向系统、汽车辅助驾驶中的路径规划系统等,都需要得到精确可靠的姿态信息。常见的测姿技术有GNSS测姿、惯性测姿以及多传感器组合测姿等。这些测姿技术中,双天线GNSS/MEMS组合测姿因为兼具MEMS惯性传感器低成本、低功耗、体积小以及双天线GNSS测向全天候、低成本、航向角精度高的优势,又可以避免惯性测姿误差随时间不断积累和GNSS测向连续性和可靠性不足的缺点,成为测姿技术中的研究热点[1-3]。在双天线GNSS/MEMS组合测姿中,陀螺得到的姿态信息具有短期精度较高的特点,一般作为姿态预报值。但随着时间推移,其误差会不断累积,因此需要利用加速度计调平得到的水平角和GNSS双天线测向得到的航向角对其进行校正。不过由于MEMS加速度计精度较低以及载体振动等的影响,加速度计输出会包含较大的噪声,导致最终调平得到的水平角误差较大,难以作为组合测姿的观测值对姿态预报值进行观测更新,因此有必要对这部分噪声进行精细的处理,以得到精确的组合测姿结果。
常用的降噪方法是在时域上对加速度计信号进行平滑,例如滑动平均滤波[4]、自适应滤波[5]、自回归滑动平均模型(ARIMA)[6]等,这些方法虽然较好地保留了载体运动的细节信息,但降噪效果有限。频域上的降噪方法包括窗函数滤波器、切比雪夫滤波器等,但截止频率相同时,两者的动态响应均较慢[4]。此外,还有小波变换降噪方法。小波分析具有多分辨率分析、降噪效果明显的特点,但其计算量大,不利于实时组合测姿系统的实现[4, 7]。
本文从频域的角度出发,对加速度计输出进行频谱分析,根据噪声主要分布在高频部分的特点,借助Butterworth滤波器,设计了一种滑动窗口的低通滤波器,用于加速度计噪声抑制。该滤波器计算量小,易于实现。经实际车载动态数据验证,该方法降噪效果明显,加速度计调平得到的水平角以及GNSS/MEMS组合测姿精度均有明显提高,因此在准确性和实时性要求较高的GNSS/MEMS组合测姿领域,具有很好的应用价值。
1 组合测姿原理 1.1 双天线GNSS/MEMS组合测姿双天线GNSS与MEMS组合可以解决GNSS测姿结果不连续的缺陷,两者融合通常使用扩展卡尔曼滤波实现。扩展卡尔曼滤波主要由状态模型和观测模型组成,常用于非线性系统。
本文的组合测姿算法为松组合,其中状态模型基于失准角误差模型建立,估计状态为地心地固坐标系(e系)下的失准角ϕ 。该线性方程可以作为一个子模块嵌入到GNSS/MEMS组合导航系统中,因此具有较好的兼容性。此外,因为MEMS陀螺通常含有较大的零偏和比例因子误差,会影响陀螺姿态信息的精度,所以状态也包括陀螺零偏bg以及比例因子Sg。
综上,状态模型如下:
| $ \left\{\begin{array}{l} {\boldsymbol{{\dot \phi }}=-\boldsymbol{R}_{b}^{e}\left(\boldsymbol{b}_{g}+\boldsymbol{S}_{g} \boldsymbol{\omega}_{b}^{b}\right)+\boldsymbol{\phi} \boldsymbol{\omega}_{i k}^{e}+\boldsymbol{\xi}_{j}} \\ {\dot{\boldsymbol{b}}_{g}=-1 / \tau_{g} \cdot \boldsymbol{b}_{g}+\boldsymbol{\xi}_{g}} \\ {\dot{\boldsymbol{S}}_{g}=-1 / \tau_{s_{c}} \cdot \boldsymbol{S}_{g}+\boldsymbol{\xi}_{s_{g}}} \end{array}\right. $ | (1) |
式中,Rbe是载体坐标系(b系)到e系的坐标转换矩阵;ωiee为地球自转角速度;零偏和比例因子误差可以通过一阶Gauss-Markov模型估计,τg和τsε是相应的相关时间;ξϕ、ξg和ξsg是估计状态的噪声谱密度,可通过Allan方差分析得到[8]。
状态模型反映状态随时间的变化情况,而观测模型则体现观测向量与状态之间的关系[9]。组合测姿模型中,估计的状态为e系下的,而姿态观测向量用欧拉角表示,它们之间的关系为:
| $ \boldsymbol{R}_{b}^{l}=\boldsymbol{R}_{e}^{l} \boldsymbol{R}_{b}^{e}=\boldsymbol{R}_{e}^{l}(\boldsymbol{I}+\boldsymbol{\phi} \times) \widetilde{\boldsymbol{R}}_{b}^{e} $ | (2) |
式中, Rbl是b系到l系(导航坐标系)的方向余弦矩阵,与欧拉角之间的关系可参考文献[9];
式(2)中姿态观测值与失准角ϕ之间的关系是非线性的,对其线性化后可以得到:
| $ \delta \mathit{\boldsymbol{z}} = \left[ {\begin{array}{*{20}{l}} {\delta \alpha }\\ {\delta \gamma }\\ {\delta \beta } \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\alpha - {\alpha _1}}\\ {\gamma - {\gamma _1}}\\ {\beta - {\beta _1}} \end{array}} \right] = \mathit{\boldsymbol{HX}} + {\mathit{\boldsymbol{w}}_m} $ | (3) |
式中,δz为姿态观测值与状态预测值之间的误差;下标I表示由陀螺得到的姿态信息;航向角观测值α来源于GNSS双天线测向,俯仰角γ和横滚角β来自加速度调平;H是设计矩阵,具体形式可由MATLAB代数计算工具得到;X为估计状态,其中包含失准角ϕ;wm为观测噪声。
1.2 水平角观测值获取双天线GNSS/MEMS组合时,航向角观测值通常由双天线GNSS测向得到,而水平角观测值使用加速度计调平。当载体静止时,重力是加速度的主要来源,此时水平角可以通过加速度计静态调平得到[10];当载体运动时,因载体运动产生的视向加速度、载体对地向心加速度等并不能直接忽略,此时载体加速度与重力之间的关系如下:
| $ {\mathit{\boldsymbol{f}}^l} = \mathit{\boldsymbol{\dot v}}_d^l + {\mathit{\boldsymbol{f}}_c} - {\mathit{\boldsymbol{g}}^l} $ | (4) |
式中,fl和gl分别是l系下的比力和重力加速度;
| $ {\mathit{\boldsymbol{f}}_c} = \left( {2\mathit{\boldsymbol{\omega }}_{ie}^l + \mathit{\boldsymbol{\omega }}_{el}^l} \right)\mathit{\boldsymbol{v}}_{el}^l $ | (5) |
式中,
实际上,加速度计输出一般为b系下的比力fb,它与fl的关系为:
| $ \boldsymbol{f}^{b}=\boldsymbol{R}_{l}^{b} \boldsymbol{f}^{l} $ | (6) |
在GNSS双天线测向得到航向角后,便可结合公式(4)~(6)计算得到水平角。
上述方法又称为加速度计动态调平,利用了GNSS位置、速度、航向角信息以及加速度计输出,解算误差不会随时间积累,因此可以作为姿态观测值去更新陀螺得到的姿态[6]。通常情况下,当模糊度固定后,GNSS位置和速度及航向角精度都比较高,因此该方法的解算精度主要受加速度计输出的影响。
2 Butterworth滤波器设计及效果分析 2.1 加速度计输出频谱分析载体运动时,MEMS加速度计的输出值除了包含其本身具有的噪声外,还包括因载体振动产生的噪声,导致水平角精度变差。由于这部分噪声来源复杂且为非平稳信号,一些基于时域的去噪方法,例如均值滤波、自适应滤波等降噪效果有限,使得水平角精度提升并不明显。因此本节将从频域角度对MEMS加速度计输出的频谱特性进行分析。
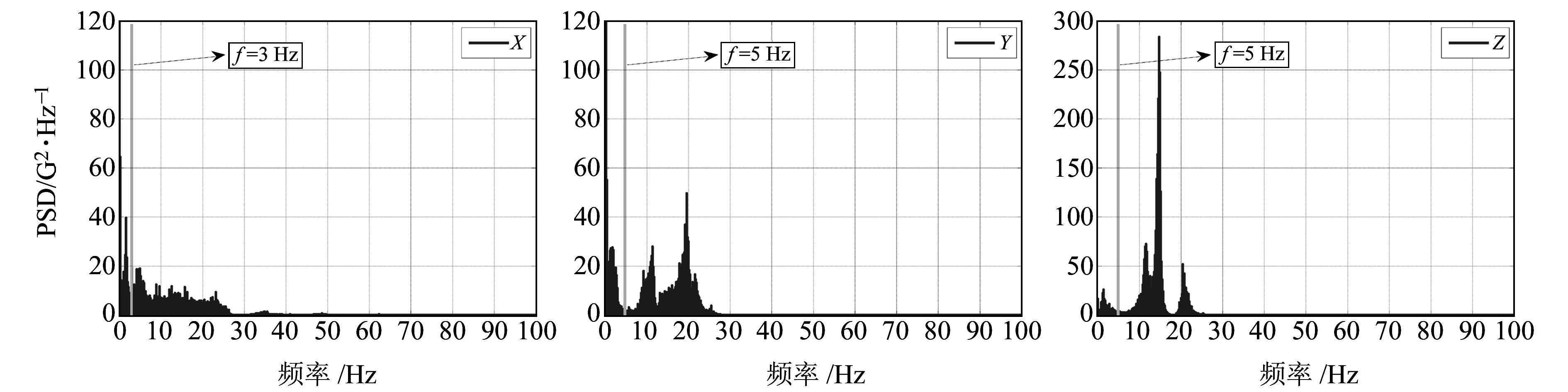
图 1是一组MEMS三轴加速度计的车载动态数据的功率谱密度,数据时长超过2 h。MEMS惯导为XSens-MTi-G-710,采样率200 Hz,其参数如表 1所示。数据采集时的设备安装情况等将在下一节详细描述。
|
图 1 三轴加速度计的功率谱密度 Fig. 1 Power spectral density of 3D-accelerometers |
|
|
表 1 SPAN-FSAS和XSens-MTi-G-710的主要性能指标 Tab. 1 Specifications of the SPAN-FSAS and XSens-MTi-G-710 |
根据图 1所示,三轴加速度计的频域分布可分为两个部分:低频部分(灰色直线左边)以及高频部分(灰色直线右边)。理论上,汽车运动时,加速度计输出仅由重力和汽车运动加速度导致,两者均属于幅度较小的低频信号,此时加速度计频谱与白噪声类似[11],因此图中的低频部分与汽车运动的加速度相关。而高频部分中,Y轴和Z轴在f=12 Hz和f=20 Hz附近有很明显的局部峰值。这是因为汽车运动时,由于特定的系统结构,车身和车辆悬架的振动会产生两组区分度比较明显且大小与汽车结构相关的固定频率[12]。这部分频率与载体实际运动的加速度无关,只是因汽车固有结构的振动而产生,所以应视为高频噪声剔除掉。至于X轴,因为是侧向轴,自由度很小,振动噪声产生的局部峰值并没有体现出来,但其在高频部分仍包含幅度较大的噪声。
2.2 Butterworth滤波器及参数设置根据§2.1分析,载体运动时加速度计的输出值包含与实际运动的加速度无关的高频振动噪声, 因此可以使用低通滤波器剔除掉。本文选择常用的Butterworth低通滤波器。
Butterworth滤波器最早由Butterworth[13]在1930提出,其具有在通带内频率响应最平滑的特性,常用于低通滤波。最基础的Butterworth低通滤波器可以被描述为:
| $ |H(w)|^{2}=\frac{1}{1+\left(\frac{w}{w_{c}}\right)^{N}} $ | (7) |
式中,w是频率,H(w)为振幅,wc为截止频率,N为滤波器的阶数。
从式(7)可以看出,其振幅特性是单调衰减。在滤波器设计时,通常先根据截止频率计算出阻带衰减,然后根据滤波器的振幅特性,计算出滤波器阶数N。通常N越大,通带内频率响应曲线越平坦,滤波器衰减速度越快[14]。
对于确定的移动载体,滤波器的截止频率可以根据信号频谱特性确定。例如图 1中,因为高频部分为振动噪声,加速度计输出的截止频率可以设置为(3 Hz,5 Hz,5 Hz),此时滤波器阶数N=4。
此外,在实时场景中,采用了滑动窗口的Butterworth低通滤波器。需要注意的是,滑动窗口长度应该适中。数据序列过短,去噪效果会变差;过长,水平角精度的提升效果则不明显,本文设置窗口长度为10 s。
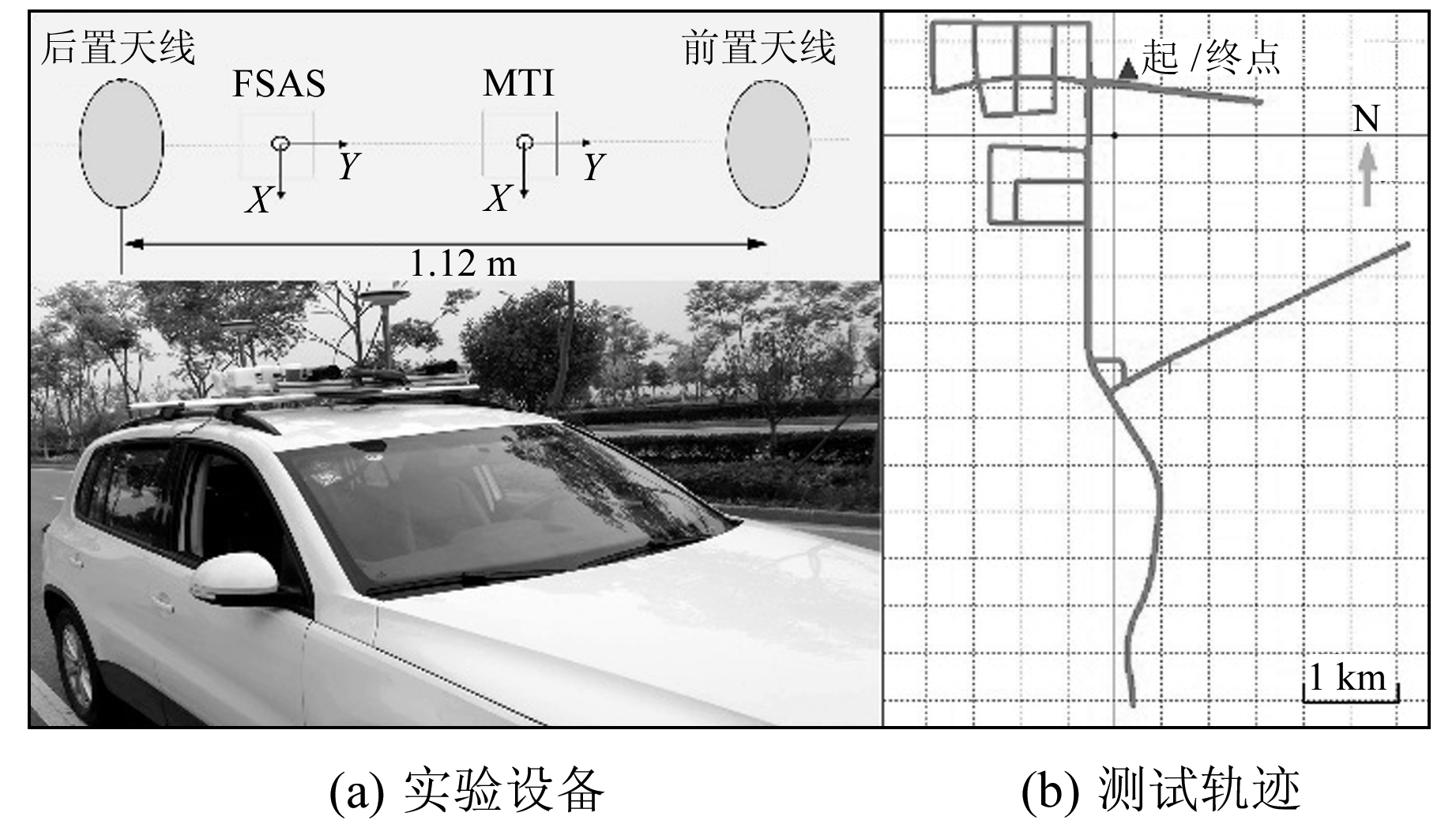
3 实验结果及分析为验证本文设计的Butterworth低通滤波器在水平角精度提升及双天线GNSS/MEMS组合测姿系统中的效果,选取一组动态车载数据进行分析。实验时使用的设备安装情况及测试轨迹如图 2所示,其中基线长度为1.12 m,GNSS采样率为1 Hz,观测条件良好。MEMS惯导为XSens-MTi-G-710,采样率为200 Hz。姿态精度评估时参考值为SPAN-FSAS/RTK松组合姿态结果,其中SPAN-FSAS是NovAtel公司生产的一款高精度惯导,其航向角标称精度0.012°,水平角0.008°。两款惯导的性能指标对比如表 1所示。
|
图 2 实验设备安装情况以及测试轨迹 Fig. 2 Equipment setup in the vehicular test and trajectory of the test |
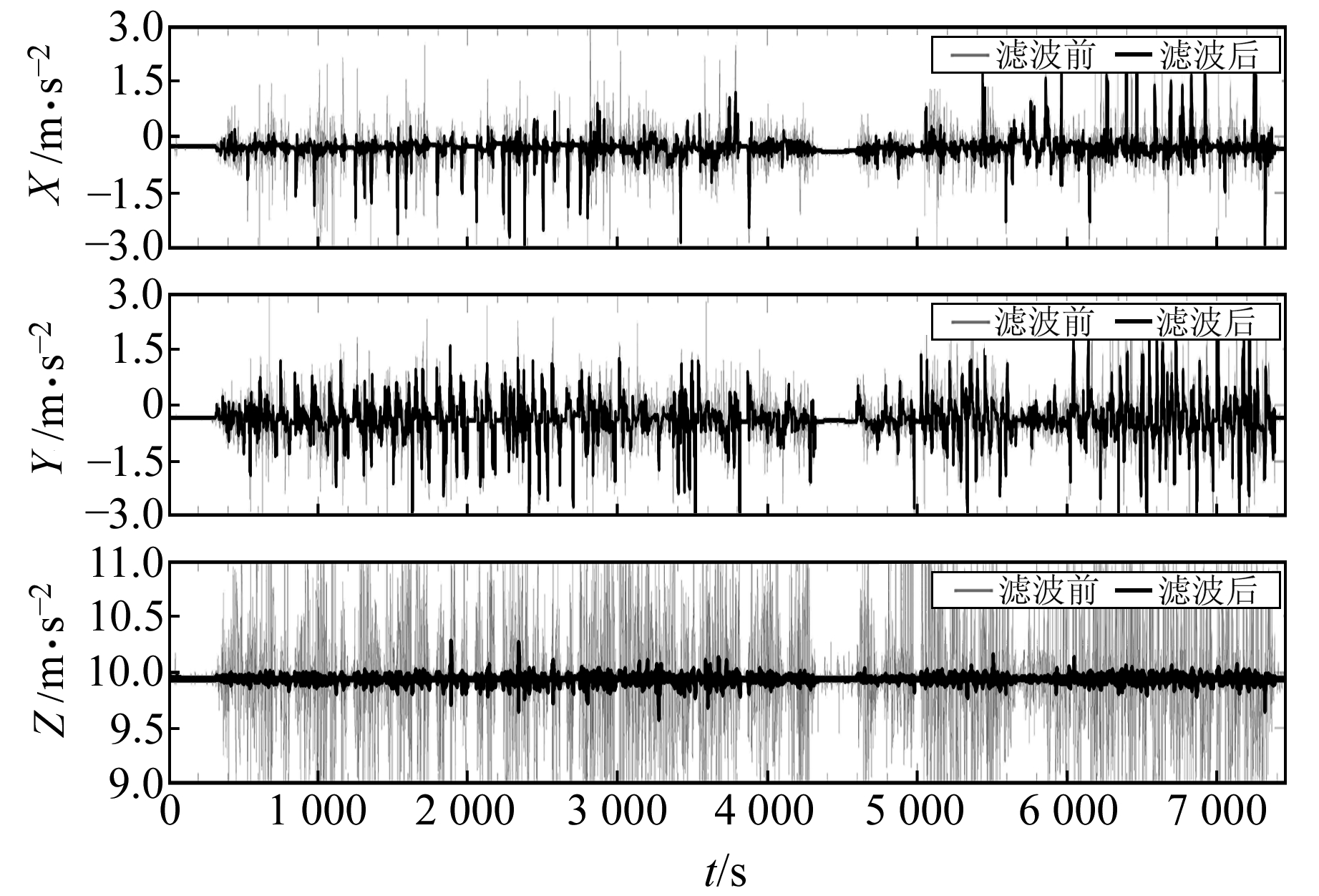
图 3是使用了§2.2中的滤波器参数后Butterworth低通滤波前后加速度计的输出序列。可以看出,与滤波前相比,滤波后的曲线更加平滑。以Z轴为例,滤波前的Z轴加速度幅值在重力加速度附近的波动超过2 m/s2,这与实际情况明显不符。这是因为,实验时汽车基本上在平整路面运动,Z轴的运动加速度输出理论上应接近重力加速度,且变化幅度很小。而经过Butterworth低通滤波后,Z轴波动明显变小,且基本上在重力加速度附近波动。以上结果说明,本文设计的Butterworth低通滤波器明显平滑了加速度计的输出结果,降噪效果显著。
|
图 3 Butterworth低通滤波前后加速度计的输出序列 Fig. 3 Time series of accelerometer measured with and without low pass filter (LF) |
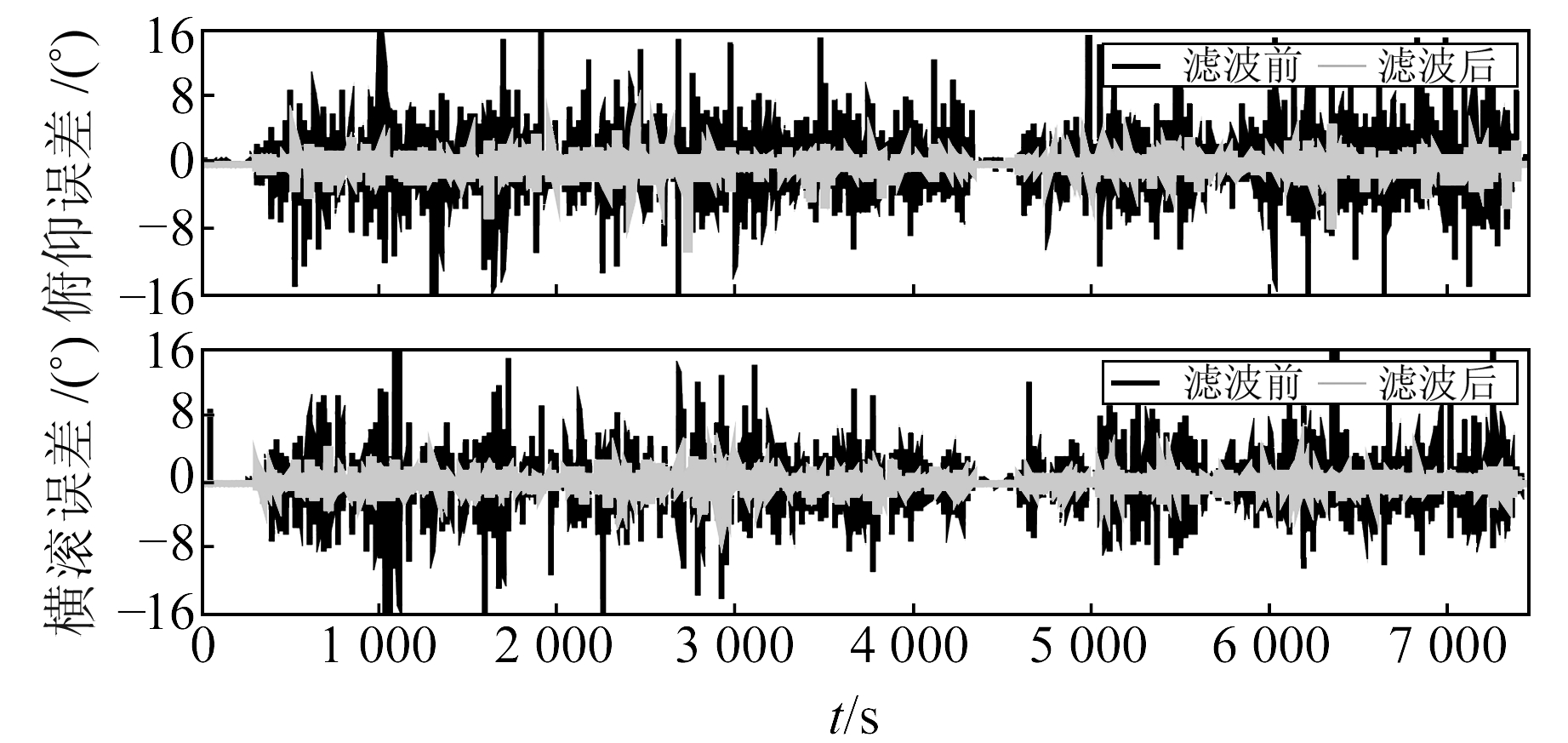
图 4是Butterworth低通滤波前后的水平角观测值误差序列。可以看出,滤波前水平角误差最大超过10°,这样大的误差会导致组合测姿结果不可靠,因此不能用于组合测姿观测更新。而滤波后大部分历元的误差都比较小,基本在4°以内。表 2(单位(°))中前两行是滤波前后水平角观测值精度的统计情况。可以得知,与滤波前相比,滤波后的水平角精度从(2.769°, 2.342°)提升到了(0.643°, 0.546°),俯仰角和横滚角精度至少提升了4倍。以上结果表明,本文设计的Butterworth低通滤波器在抑制MEMS加速度计高频振动噪声方面效果明显,水平角观测值的精度有了明显提升。
|
图 4 Butterworth低通滤波前后水平角误差序列 Fig. 4 Error series of accelerometers derived horizontal angles with and without low pass filter (LF) |
|
|
表 2 低通滤波前后姿态精度RMS统计结果 Tab. 2 Attitude solution RMS with and without low pass filter(LF) |
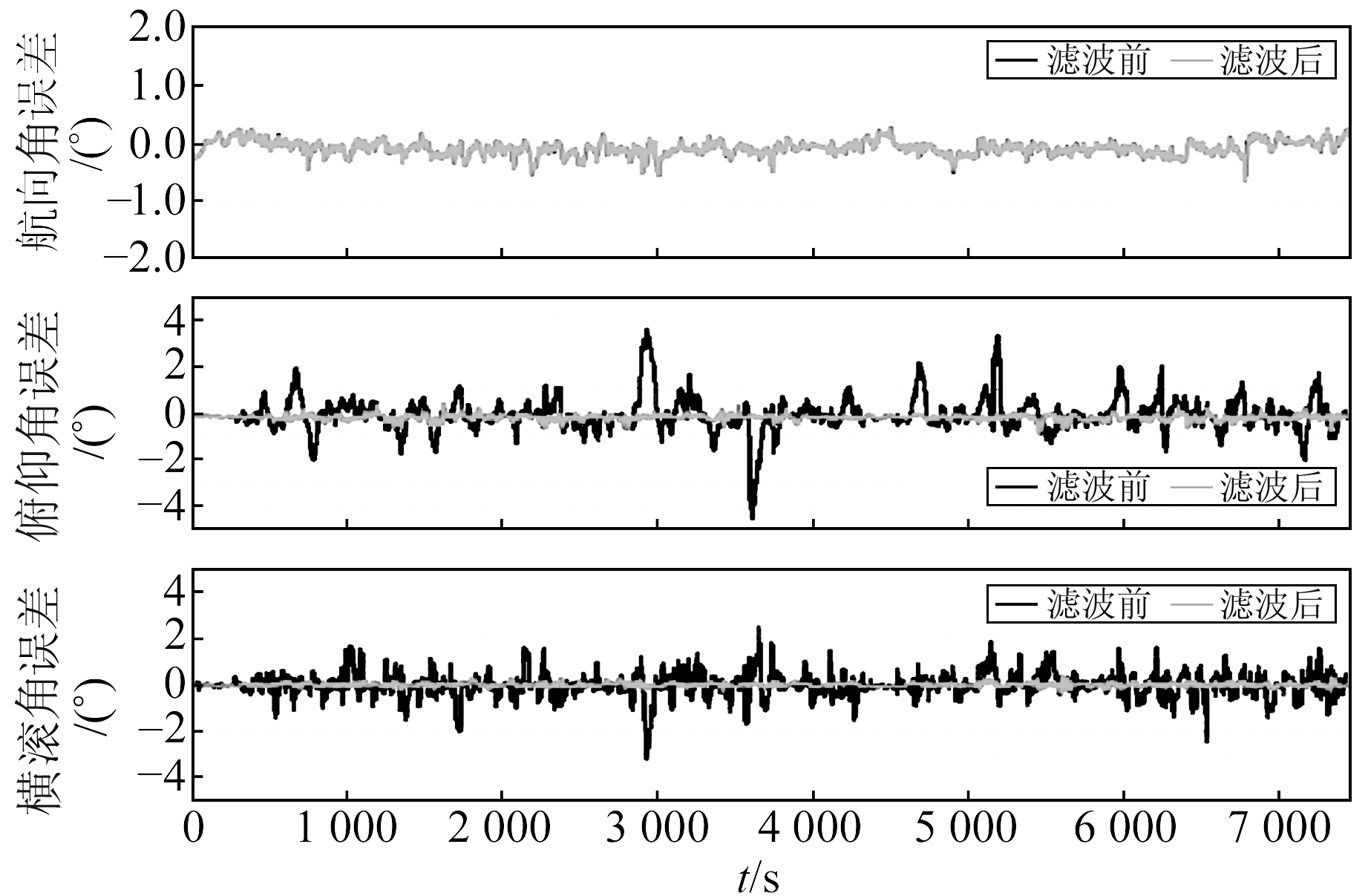
图 5是低通滤波前后双天线GNSS/MEMS组合测姿的结果。可以看出,除了航向角以外,滤波前组合测姿结果误差波动明显更大,误差最大时接近5°;滤波后组合测姿误差均在1°以内,波动也较小。因为Butterworth低通滤波提升的是水平角观测值的精度,航向角误差曲线变化并不明显。但水平角由于观测值精度的提升,使得滤波后组合测姿误差曲线明显比滤波前更平滑。表 2(单位(°))后两行统计了滤波前后组合测姿结果的精度。可以看到,滤波后姿态角误差RMS从(0.124°, 0.738°, 0.532°)下降到(0.122°, 0.074°, 0.052°)。虽然航向角提升不够明显,但使用Butterworth低通滤波后,组合测姿水平角精度明显提高,提升了大约一个数量级。
|
图 5 Butterworth低通滤波前后组合测姿结果 Fig. 5 Error series of GNSS/MEMS attitude with and without low pass filter (LF) |
本文通过对实际车载运动中加速度计输出进行频谱分析发现,其高频部分含有因汽车固有结构产生的高频振动噪声。基于此,借助滑动窗口的Butterworth低通滤波器,进行低精度、低成本的MEMS加速度计的振动噪声剔除,进而提高加速度计动态调平得到的水平角观测值的精度以及双天线GNSS/MEMS组合测姿的精度。车载实验结果表明,该滤波器降噪效果明显,滤波后水平角观测值的精度有了明显提升。与滤波前相比,俯仰角和横滚角精度至少提升了4倍。此外,组合测姿精度也从(0.122°, 0.738°, 0.532°)提升到(0.124°, 0.074°, 0.052°),其中水平角的精度提升了大约一个数量级。因此,采用Butterworth低通滤波器的双天线GNSS/MEMS组合测姿精度更高、结果更可靠。
| [1] |
Wu Z, Yao M, Ma H, et al. Low-Cost Attitude Estimation with MIMU and Two-Antenna GPS for Satcom-on-the-Move[J]. GPS Solutions, 2013, 17(1): 75-87 DOI:10.1007/s10291-012-0262-z
(  0) 0) |
| [2] |
Yang Y, Farrell J A. Two Antennas GPS-Aided INS for Attitude Determination[J]. IEEE Transactions on Control Systems Technology, 2003, 11(6): 905-918 DOI:10.1109/TCST.2003.815545
(  0) 0) |
| [3] |
Zhang L, Han D, Dezert J. Full-Dimension Attitude Determination Based on Two-Antenna GPS/SINS Integrated Navigation System[C]. International Conference on Information Fusion, 2017
(  0) 0) |
| [4] |
Jan R, Michal R, Karel D. Data Processing of Inertial Sensors in Strong-Vibration Environment[C]. IEEE International Conference on Intelligent Data Acquisition & Advanced Computing Systems, 2011
(  0) 0) |
| [5] |
秦国庆, 赖际舟, 陈驵, 等. 捷联航姿系统加速度计振动噪声平滑技术[J]. 电子测量技术, 2013, 36(4): 87-91 (Qin Guoqing, Lai Jizhou, Chen Zang, et al. Vibration Noise Smooth Technique for Accelerometers of AHRS[J]. Electronic Measurement Technology, 2013, 36(4): 87-91 DOI:10.3969/j.issn.1002-7300.2013.04.021)
(  0) 0) |
| [6] |
钱伟行.捷联惯导与组合导航系统高精度初始对准技术研究[D].南京: 南京航空航天大学, 2010 (Qian Weixing. Research on High-Precision Initial Alignment of Strap down Inertial and Integrated Navigation System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010)
(  0) 0) |
| [7] |
Wu P, Ge Y, Chen S, et al. Denoising Algorithm Based on Compression of Wavelet Coefficient for MEMS Accelerometer Signal[C]. IEEE International Conference on Information and Automation, 2010
(  0) 0) |
| [8] |
Yang L, Li Y, Wu Y, et al. An Enhanced MEMS-INS/GNSS Integrated System with Fault Detection and Exclusion Capability for Land Vehicle Navigation in Urban Areas[J]. GPS Solutions, 2014, 18(4): 593-603 DOI:10.1007/s10291-013-0357-1
(  0) 0) |
| [9] |
Groves P. GNSS与惯性及多传感器组合导航系统原理[M]. 第2版. 北京: 国防工业出版社, 2015 (Groves P. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. Edition 2. Beijing: National Defense Industry Press, 2015)
(  0) 0) |
| [10] |
Lai Y C, Jan S S. Attitude Estimation Based on Fusion of Gyroscopes and Single Antenna GPS for Small UAVs under the Influence of Vibration[J]. GPS Solutions, 2011, 15(1): 67-77 DOI:10.1007/s10291-010-0171-y
(  0) 0) |
| [11] |
Ramanandan A. High Accuracy Sensor Aided Inertial Navigation Systems[D]. Riverside: University of California Riverside, 2011
(  0) 0) |
| [12] |
Barbosa R S. Vehicle Vibration Response Subjected to Longwave Measured Pavement Irregularity[J]. Journal of Mechanical Engineering and Automation, 2012, 2(2): 17-24 DOI:10.5923/j.jmea.20120202.04
(  0) 0) |
| [13] |
Acharya A, Das S, Pan I, et al. Extending the Concept of Analog Butterworth Filter for Fractional Order Systems[J]. Signal Processing, 2014, 94: 409-420 DOI:10.1016/j.sigpro.2013.07.012
(  0) 0) |
| [14] |
王珂, 肖鹏峰, 冯学智, 等. 二维Log Butterworth滤波器全方向边缘检测的频域实现方法[J]. 测绘学报, 2013, 42(5): 682-690 (Wang Ke, Xiao Pengfeng, Feng Xuezhi, et al. Omnidirectional Edge Detection Using 2D Log Butterworth Filters in Frequency Domain[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 682-690)
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2020, Vol. 40
2020, Vol. 40

