在GPS数据处理中,接收机故障、粗差剔除以及其他未知原因会导致解算异常,从而使获得的GPS坐标时间序列数据缺失,特别是对于长期观测的GPS基准站,其数据缺失现象普遍存在[1]。若缺失数据比例过大,则在时间域上对坐标序列建模时必然影响参数(尤其是测站速度)估计的精度;而在频率域上对其进行谱分析时,则会导致混频现象。因此,在对GPS时间序列进行分析之前,必须要进行数据预处理,其中一个非常重要的过程就是插值,通过对缺失数据插补以获得均匀采样的时间序列[2]。
目前,已有众多学者对GPS坐标时间序列缺失数据插值进行了相关研究。武艳强等[3]提出多点三次样条插值方法,该方法可以在一定条件下解决时间序列处理中较多数据缺失的问题;田慧等[4]将正交多项式方法应用到GPS时间序列插值中,在数据缺失量增多特别是数据连续缺失较多时,此方法可以较好地保持原有序列的运动趋势。根据已有的研究成果,当GPS基准站坐标时间序列连续缺损数据不超过3个时,拉格朗日插值方法(Lagrange)是最适合的插值方法;当缺损数据不超过15个时,线性内插或者三次样条方法是最适合的插值方法;当连续缺损数据的数量更多时,可采用正交多项式拟合插值方法。然而,上述方法本身基于纯数学模型,没有考虑GPS坐标时间序列的物理背景,因而其在物理意义上是不充分的,特别是对于季节性信号比较明显的时间序列,在数据大量缺失时其插值效果会明显变差。这类插值方法可以将其归为基于数学模型的插值方法,简称模型驱动法(model-driven method)[5]。
本文将气象学中广泛应用的一种插值方法——调整最大似然法(regularized EM algorithm,RegEM)引入到GPS时间序列插值中来。该方法不依赖任何外部数学模型,也不引入任何外部先验信息,而是根据数据本身的特性进行插值,因此可以将其归为基于数据本身特性的插值方法,简称数据驱动法(date-driven method)。Mann等[6]曾利用该方法重建了1500年以来的全球温度序列。罗文等[7]应用RegEM等方法对西北太平洋区域海面变化进行了预测。本文首先对RegEM方法进行简要介绍,然后引入几项插值性能评价指标,并对比分析RegEM和传统插值方法对于模拟不同比例连续缺失数据与实测含缺失数据的插值性能与效果。
1 算法原理及评价指标 1.1 RegEM插值算法基本原理调整最大似然估计算法是由Schneider提出的用于气候数据缺失填补的一种迭代方法[8]。该方法以岭回归方法实现回归正则化及参数估计,利用交叉检验实现给定精度的时空矩阵插值。因此,该算法不仅能够估计缺失数据,还可以估计同时性和历时性的协方差阵,以分析其可能包含的空间协变、平稳时间协变或周期平稳的时间协变信息[7]。
RegEM插值算法基本原理如下:
设X为n×p维观测矩阵(列向量中包含缺失数据),n为观测历元数,p为变量个数(即测站个数),一般满足n>p。X的待估均值和协方差阵分别为μ ∈R1×p、Σ ∈Rp×p。设某一历元i所有测站的坐标向量为Xi:(Xi:表示X中第i行有数据缺失),历元i时刻pa个非缺失的测站坐标构成的向量为xa∈R1×pa,剩余pm个缺失的测站坐标构成的向量为xm∈R1×pm。进一步,设x a的均值为
| $ \boldsymbol{x}_{m}=\boldsymbol{\mu}_{m}+\left(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a}\right) \boldsymbol{B}+\boldsymbol{e} $ | (1) |
式中,矩阵
| $ \hat{\boldsymbol{x}}_{m}=\hat{\boldsymbol{\mu}}_{m}+\left(\boldsymbol{x}_{a}-\hat{\boldsymbol{\mu}}_{a}\right) \hat{\boldsymbol{B}} $ | (2) |
式中,
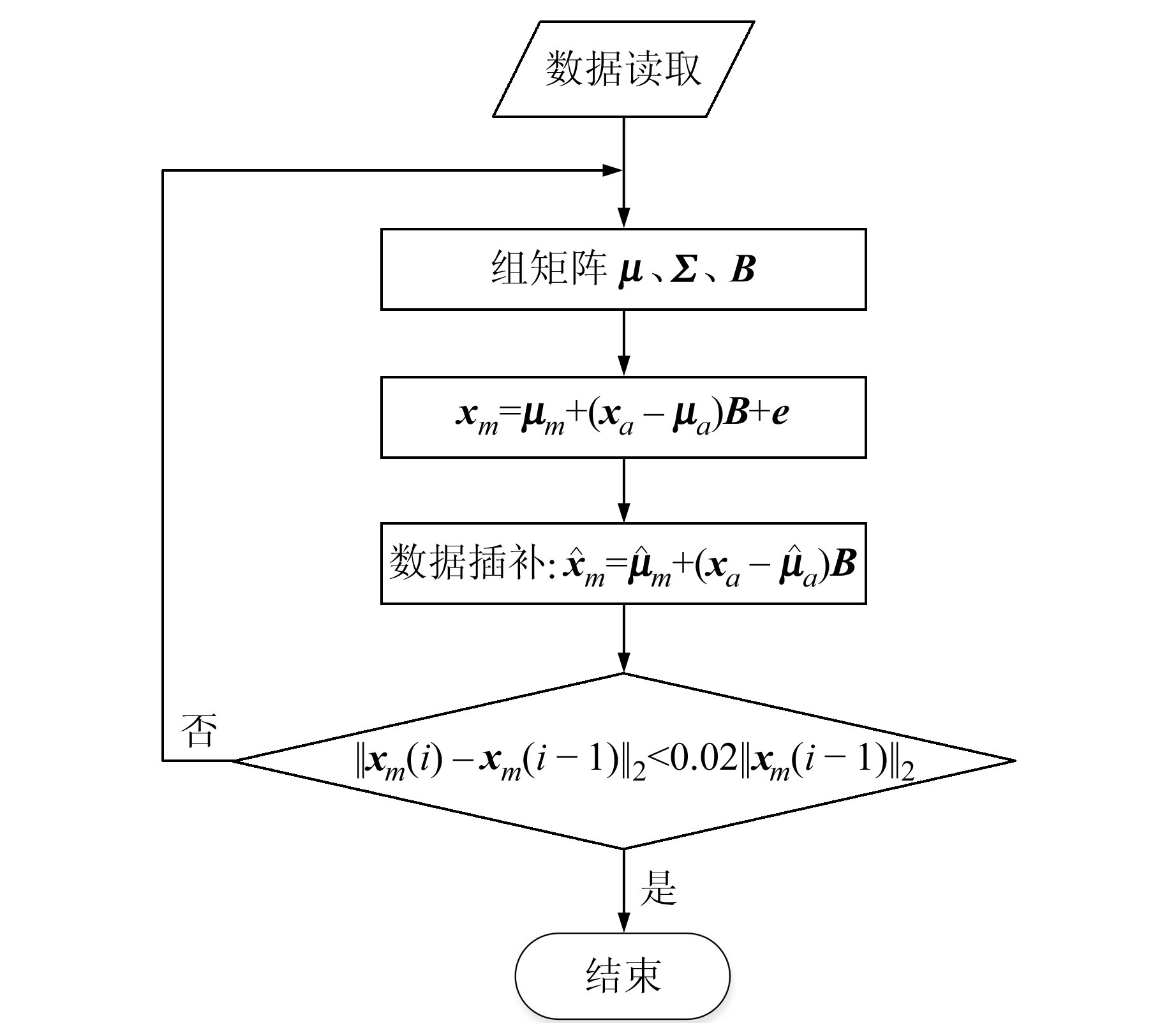
|
图 1 算法流程 Fig. 1 Algorithm flow |
需要指出的是,式(1)中回归系数B通过岭估计得到。在每一次迭代中,通过k阶交叉核实(k-fold cross-validation,KCV)对每一行观测值自适应地选择正则化参数(程序中省缺值k=5)。
1.2 评价指标为对比不同算法的插值效果,对于人为打断部分序列数据的情况,采用GPS坐标时间序列真实值和插补值之间的平均绝对值误差(mean absolute error,MAE)、Pearson相关系数以及Spearman相关系数3个指标进行评估。
1) MAE的计算公式为:
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{k=1}^{n} | \text { pred }_{k}-\text { obs }_{k} | $ | (3) |
式中,predk、obsk分别为第k个插补值和真实值(观测值)。MAE值越小,说明插值效果越好。
2) Pearson相关系数的计算公式为[9]:
| $ r_{\mathrm{p}}=\frac{n \sum\limits_{k=1}^{n} \operatorname{pred}_{k} \cdot \mathrm{obs}_{k}-\sum\limits_{k=1}^{n} \operatorname{pred}_{k} \sum\limits_{k=1}^{n} \mathrm{obs}_{k}}{\sqrt{n \sum\limits_{k=1}^{n} \operatorname{pred}_{k}^{2}-\left(\sum\limits_{k=1}^{n} \operatorname{pred}_{k}\right)^{2}} \sqrt{n \sum\limits_{k=1}^{n} \mathrm{obs}_{k}^{2}-\left(\sum\limits_{k=1}^{n} \mathrm{obs}_{k}\right)^{2}}} $ | (4) |
式中,rp表示Pearson相关系数,其绝对值越大,表示predk和obsk的相关性越强,则插值效果越好。
3) Spearman相关系数的计算公式为:
| $ {r_{\rm{s}}} = 1 - \frac{{6\sum\limits_{k = 1}^n {{{\left( {{{{\mathop{\rm pred}\nolimits} }_k} - {\rm{ob}}{{\rm{s}}_k}} \right)}^2}} }}{{n\left( {{n^2} - 1} \right)}} $ | (5) |
式中,rs表示Spearman相关系数,其取值在-1~1之间(与Pearson相关系数相同),其绝对值越大,表示predk和obsk的相关性越强,则插值效果越好。
对于实测数据中的序列值缺失,没有真实值作为参考,无法使用上述3种指标评价插值效果。本文参考文献[5]的方法,采用插值后的观测网时间序列投影到各主方向后的方差,评估各插值方法的效果。各主方向上的方差的计算公式为[10]:
| $ \boldsymbol{v}_{j}=\boldsymbol{w}_{j}^{\mathrm{T}} \boldsymbol{S} \boldsymbol{w}_{j} $ | (6) |
式中,wj为第j个主方向,
为了比较不同算法的插值效果,并在实验中保留时间序列数据本身的物理特性,实验采用SOPAC提供的ITRF2005框架下的IGS站单天解坐标时间序列,测站选取中国区域的BJFS、WUHN、URUM、KUNM等4个IGS站,时间跨度为1996.370~2018.780。为避免粗差、阶跃等因素的影响,采用去粗差后的残差时间序列。选取测站残差序列如图 2所示。

|
图 2 原始残差序列 Fig. 2 Original residual series |
为比较RegEM算法在不同数据缺失比例条件下的插值效果,人为模拟设置3种不同的数据缺失比例:方案1,缺失数据7个(7 d);方案2,缺失数据30个(30 d);方案3,缺失数据180个(180 d)。由于篇幅限制,本文仅给出KUNM站高程方向上残差序列的插值实验结果分析。
2.2.1 方案1此方案主要针对连续缺失数据较少的情况,人为打断2005年年积日169~176共计7 d的序列点(历元为2005.464~2005.485)。分别采用拉格朗日、三次样条、正交多项式与RegEM方法进行插值,分析对比插值性能与效果。
如图 3所示,缺失少量数据时,各种插值方法均能大致保持原始时间序列的运动趋势。但将图中插值部分放大后(图 4)可见,在序列较为平稳的阶段,各方法插值效果较好,随着序列发生较大的趋势变化,拉格朗日插值方法与其他方法相比效果最差;三次样条方法和正交多项式拟合插值方法效果基本保持一致,这也与已有的研究成果相符合;RegEM算法由于结合了序列本身数据的特性,同样能较好地保持序列的趋势性,且效果稍优于三次样条与正交多项式。由表 1可以看出,由于所选取缺失序列值数量级较小,对于MAE指标,RegEM算法明显优于其他方法;对于相关系数,则与其他方法差异不大。

|
图 3 插值后的GPS时间序列(缺失7 d数据) Fig. 3 GPS time series after interpolation (missing 7 d data) |
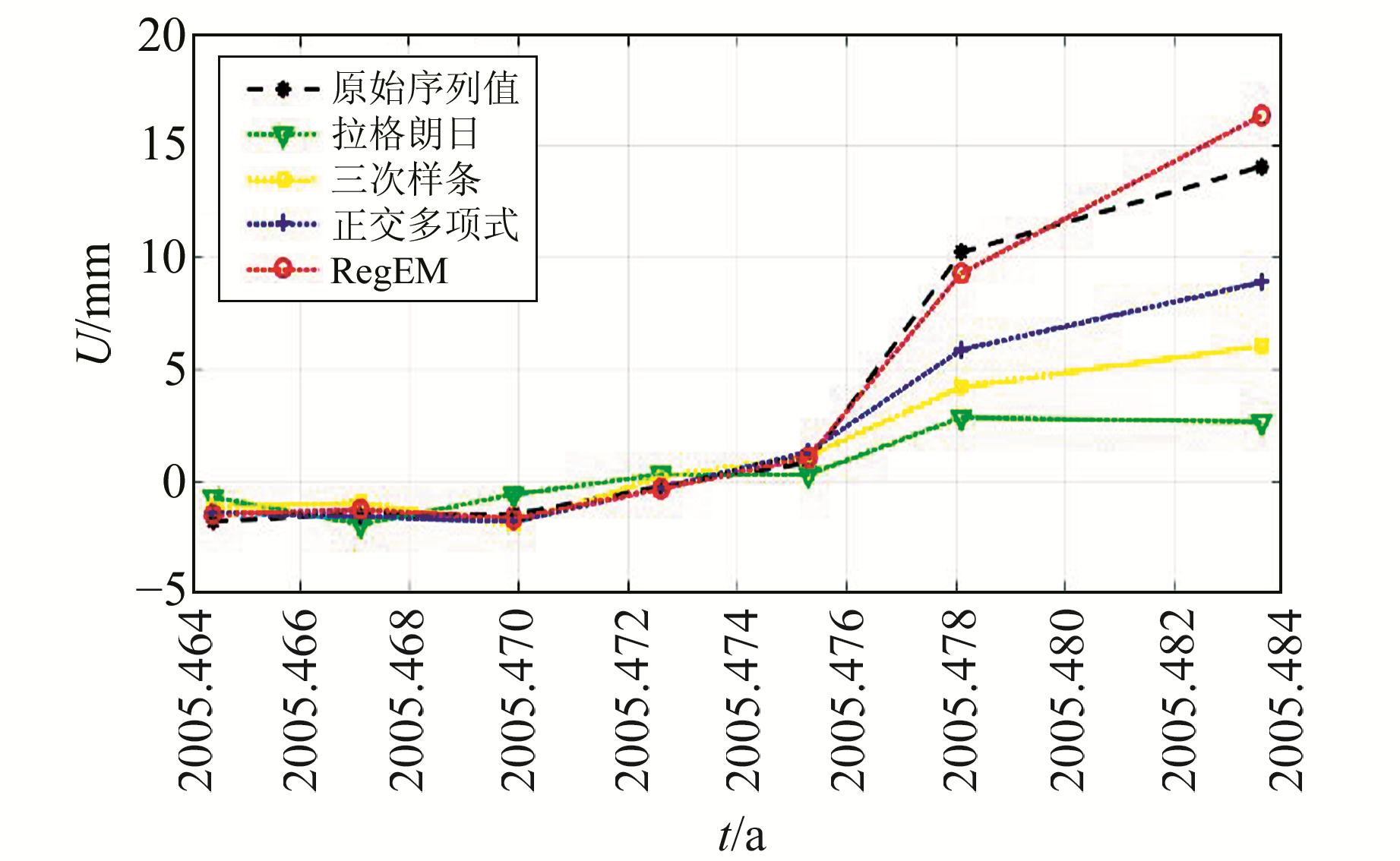
|
图 4 不同方法插值效果的对比(缺失7 d数据) Fig. 4 Comparison of interpolation effects of different methods(missing 7 d data) |
|
|
表 1 不同插值方法性能的对比(缺失7 d数据) Tab. 1 Performance comparison of different interpolation methods(missing 7 d data) |
此方案主要针对连续缺失数据较多的情况进行分析,人为打断2008年年积日336~365共计30 d的序列点(历元为2008.919~ 2008.998)。以往研究成果表明,在缺失数据较多时拉格朗日方法不再适用,故只采用三次样条、正交多项式和RegEM方法进行插值分析。
3种方法插值后的时间序列与原始序列的对比如图 5所示,在缺失30 d数据的情况下,3种插值方法仍然可以大致保持序列原有的运动趋势,但是可以看出,正交多项式方法使插补数据趋于线性化。放大插值部分后这种现象更加明显(图 6)。三次样条方法插补数据产生突变现象,与原始时间序列运动趋势有较大偏离;正交多项式方法插补数据较为平稳,但是使得整体趋势趋于线性化;RegEM算法插补数据与原始序列趋势符合较好,且没有产生突变现象。3个评价指标的量化比较见表 2,对于MAE指标,RegEM方法明显优于其他方法,三次样条方法与正交多项式方法则大致处于相同水平;对于相关系数,RegEM方法明显最优,三次样条方法次之,正交多项式方法由于插补数据过于平稳,相关系数值最小。
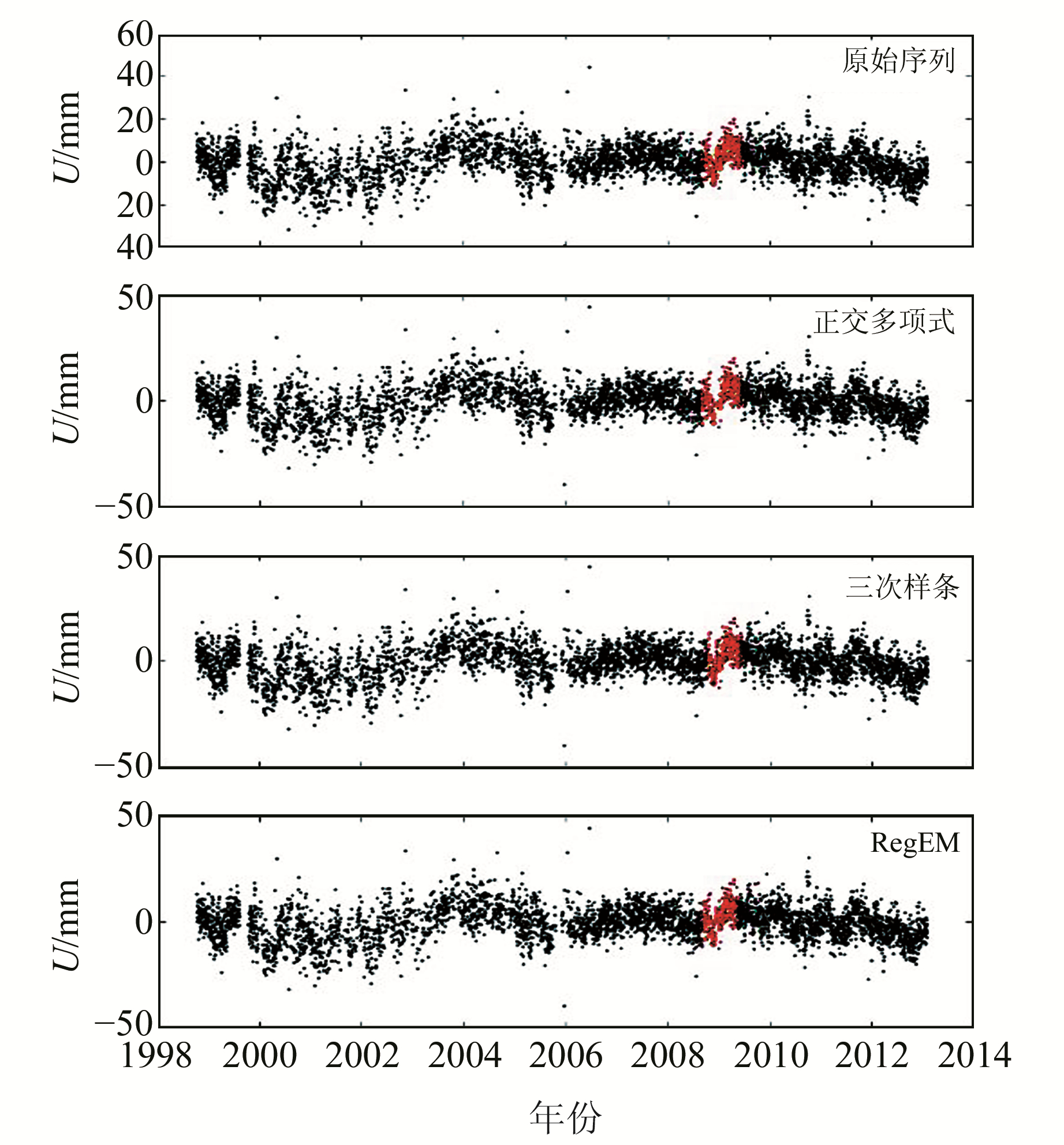
|
图 5 插值后的GPS时间序列(缺失30 d数据) Fig. 5 GPS time series after interpolation (missing 30 d data) |
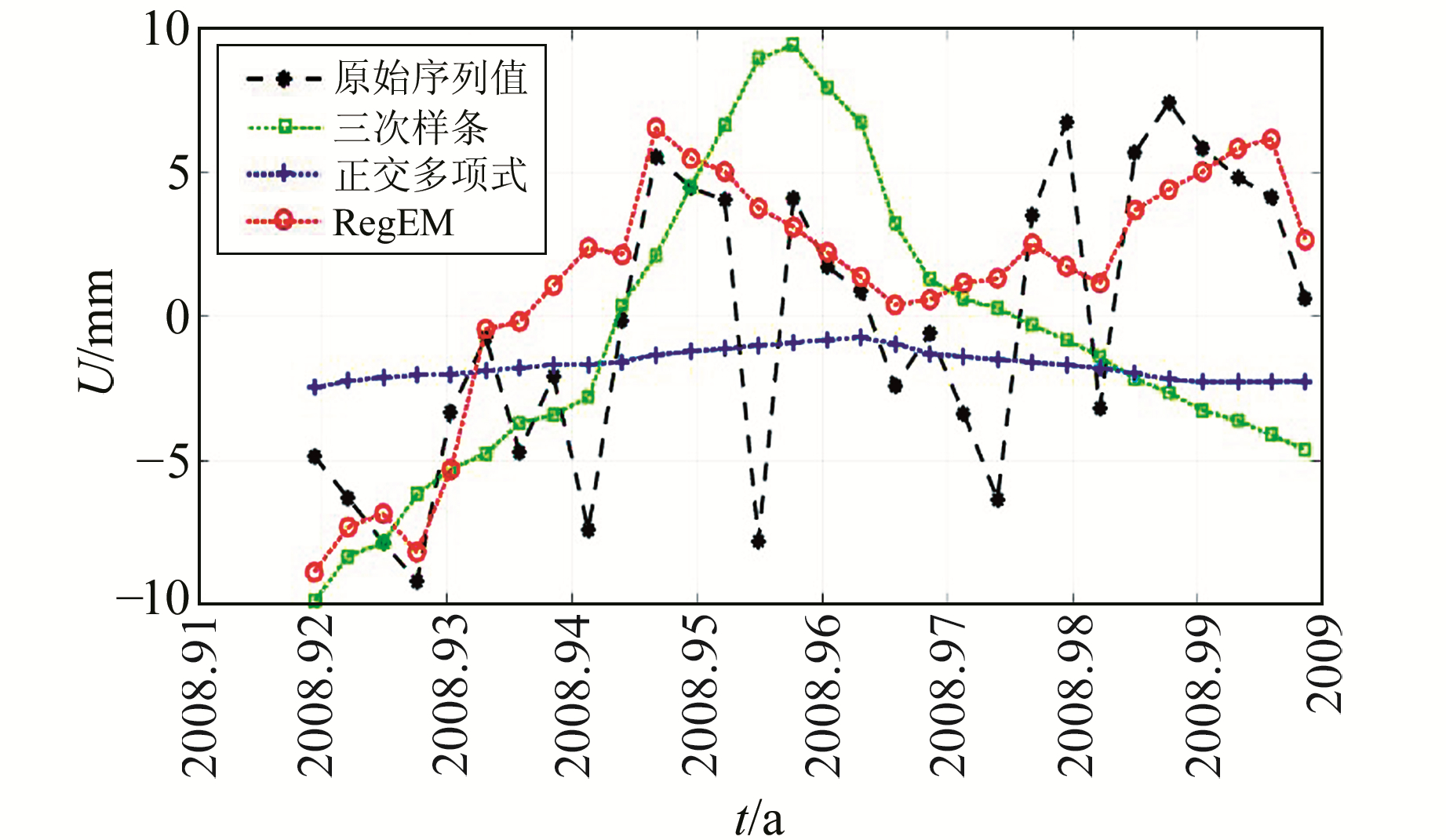
|
图 6 不同方法插值效果的对比(缺失30 d数据) Fig. 6 Comparison of interpolation effects of different methods(missing 30 d data) |
|
|
表 2 不同插值方法性能的对比(缺失30 d数据) Tab. 2 Performance comparison of different interpolation methods(missing 30 d data) |
此方案主要针对时间序列有大量连续缺失的情况进行分析,人为打断2009年年积日001~180共计180 d的序列点(历元为2009.001~2009.495),约占总数据量的5%。本方案仍然采用三次样条、正交多项式和RegEM方法进行插值分析。
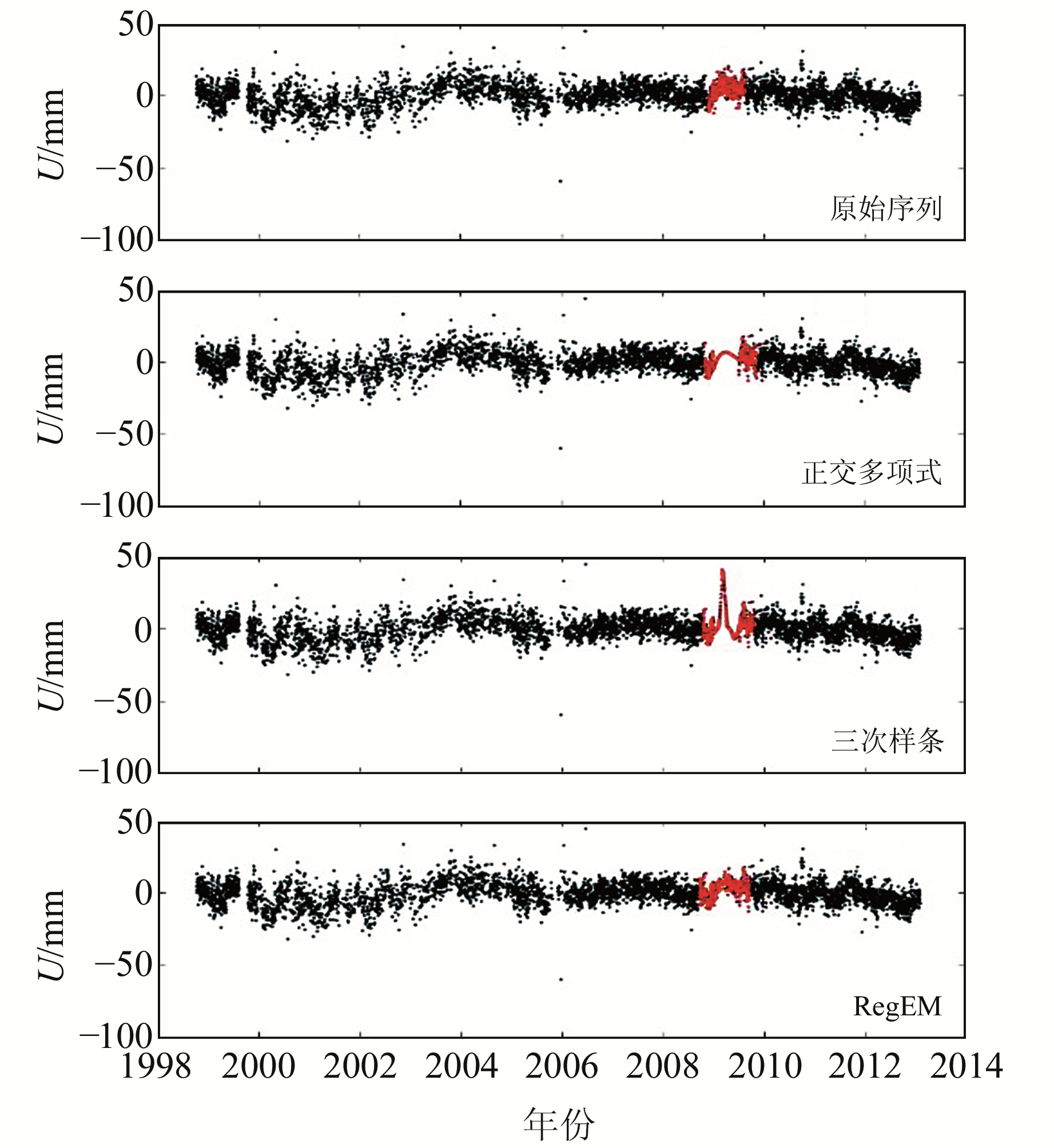
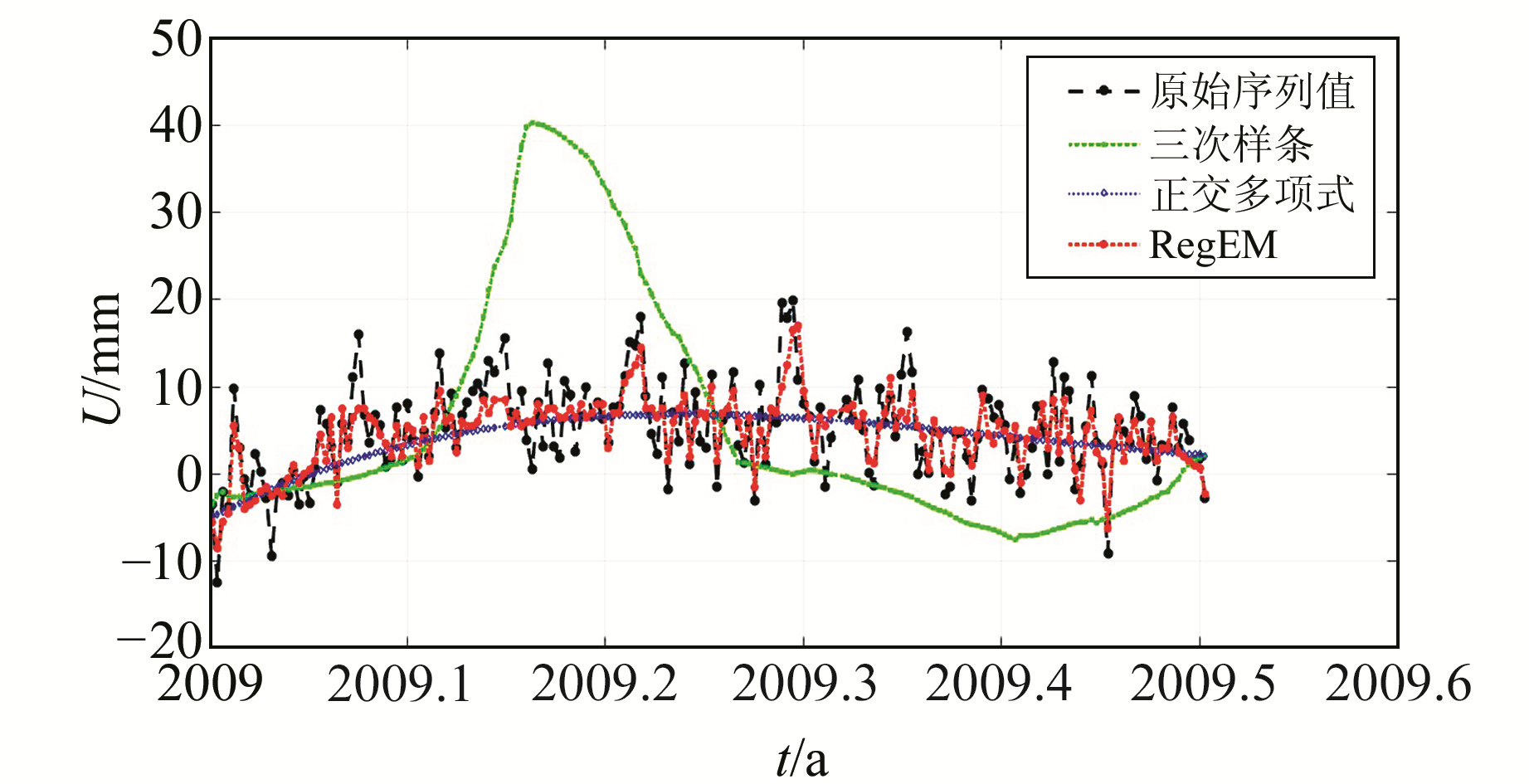
3种方法插值后时间序列与原始序列对比如图 7所示,在大量缺失数据时,3种插值方法插值效果有明显的差异。本次实验人为打断的序列呈现0.5 a的周期特性,三次样条方法所得插补值明显地产生了突变;而正交多项式插值方法使插补数据趋于光滑;RegEM方法由于是基于数据本身的协方差特性,对于此种具有0.5 a周期特性的缺失数据插补显然更有优势。放大插值部分后这种现象更加明显(图 8)。3个评价指标的量化对比方面,RegEM方法均优于三次样条方法和正交多项式插值方法。对比RegEM方法在不同数据缺失比例情况下的MAE、Pearson相关系数和Spearman相关系数可以发现,随着数据缺失比例变大,插值效果也逐渐变差(表 3)。
|
图 7 插值后的GPS时间序列(缺失180 d数据) Fig. 7 GPS time series after interpolation (missing 180 d data) |
|
图 8 不同方法插值效果的对比(缺失180 d数据) Fig. 8 Comparison of interpolation effects of different methods(missing 180 d data) |
|
|
表 3 不同插值方法性能对比(缺失180 d数据) Tab. 3 Performance comparison of different interpolation methods(missing 180 d data) |
选取的4个IGS站数据为去粗差后的残差时间序列(clean resid),由于仪器故障、粗差剔除以及阶跃变化等因素影响,序列中已经有部分数据缺失。经统计,4个站高程方向平均数据缺失率较大(约为24.7%),分析其原因,可能为早期IGS站仪器故障、数据质量等导致。采用三次样条、正交多项式以及RegEM方法分别对选取序列进行插值,计算插值后所得序列各方向上的方差,并统计各插值方法前3个主方向所占总方差的百分比(见表 4,单位%)。
|
|
表 4 不同插值方法前3个主成分方差占比 Tab. 4 Variance ratio of the first three principal components of different interpolation methods |
插值后的时间序列应该尽可能保持原有方差的最大化方向,对比表 4中各个方法插值后前3个主成分之和占总方差的百分比可以看出,RegEM方法插值所得序列保留方差最大,约为正交多项式方法的1.17倍、三次样条方法的1.38倍。值得提出的是,对于本次实验所选数据缺失率较大、数据历元总量较大的情况,RegEM方法由于需要计算X的协方差矩阵且循环迭代计算效率低,相对于其他方法有着明显的不足。
3 结语通过选取模拟不同比例连续缺失数据与实测含缺失数据进行实验,对比分析拉格朗日插值、三次样条插值、正交多项式拟合插值与RegEM方法的插值效果,得出以下几点结论:
1) 当数据缺失较少时,在数据变化较为平缓的阶段,拉格朗日、三次样条、正交多项式插值效果相当,这也与已有研究成果相符;但数据发生较大变化时,正交多项式插值与RegEM对数据变化较为敏感,能更好地反映序列的运动趋势。
2) 当数据缺失较多时,拉格朗日方法不再适用;三次样条方法会使序列值发生突变,偏离原有序列运动趋势;正交多项式方法则会使插值序列变得光滑且趋于线性化,能保持序列总体运动趋势,但细节方面效果较差;而RegEM方法则既能保持序列总体趋势,且在细节方面的插值效果优于正交多项式方法。
3) 当数据大量缺失时,特别是当缺失数据具有0.5 a周期性等季节性特性的情况下,三次样条插值会使数据严重突变并偏离原有序列运动趋势,正交多项式方法则使数据过于光滑。相较而言,RegEM方法在各方面均优于其他方法。
4) 对于实测含缺失数据,RegEM方法由于顾及了序列数据本身的物理特性,插值后的序列能更好地保持原有序列方差最大化方向,但计算效率方面有所不足。
| [1] |
占伟, 黄立人, 刘志广, 等. 数据缺失对GNSS时间序列分析的影响[J]. 大地测量与地球动力学, 2013, 33(2): 49-53 (Zhan Wei, Huang Liren, Liu Zhiguang, et al. Influence of Data Deficiency on GPS Time Series Analysis[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 49-53)
(  0) 0) |
| [2] |
Griffiths J, Ray J. Impacts of GPS Coordinate Offsets on Global Frame Stability[J]. Geophys J Int, 2016, 204: 480-487 DOI:10.1093/gji/ggv455
(  0) 0) |
| [3] |
武艳强, 黄立人. 时间序列处理的新插值方法[J]. 大地测量与地球动力学, 2004, 24(4): 43-47 (Wu Yanqiang, Huang Liren. A New Interpolation Method for Time Series Processing[J]. Journal of Geodesy and Geodynamics, 2004, 24(4): 43-47)
(  0) 0) |
| [4] |
田慧, 程鹏飞, 秘金钟. 不同插值方法对CORS高程时间序列的影响分析[J]. 测绘科学, 2013, 38(1): 16-17 (Tian Hui, Cheng Pengfei, Bei Jinzhong. Influence of Different Interpolation Methods on CORS Elevation Time Series[J]. Science of Surveying and Mapping, 2013, 38(1): 16-17)
(  0) 0) |
| [5] |
明锋, 曾安敏, 勾万祥, 等. 数据驱动插值法对GNSS坐标时间序列敏感性分析[J]. 测绘科学与工程, 2016(5): 4-9 (Ming Feng, Zeng Anmin, Gou Wanxiang, et al. Sensitivity Analysis of GNSS Coordinate Time Series Based on Data Driven Interpolation Method[J]. Journal of Surveying and Mapping Science and Engineering, 2016(5): 4-9)
(  0) 0) |
| [6] |
Mann M E, Zhang Z, Rutherford S, et al. Global Signatures and Dynamical Origins of the Little Ice Age and Medieval Climate Anomaly[J]. Science, 2009, 326: 1 256-1 260 DOI:10.1126/science.1177303
(  0) 0) |
| [7] |
罗文, 袁林旺, 易琳, 等. 基于验潮数据的西北太平洋区域海面变化预测[J]. 地理学报, 2011, 66(1): 111-122 (Luo Wen, Yuan Linwang, Yi Lin, et al. Prediction of Sea Surface Change in the Northwest Pacific Based on Tide Data[J]. Acta Geographica Sinica, 2011, 66(1): 111-122)
(  0) 0) |
| [8] |
Schneider T. Analysis of Incomplete Climate Data: Estimation of Mean Values and Covariance Matrices and Imputation of Missing Values[J]. Journal of Climate, 2001, 14(5): 853-871 DOI:10.1175/1520-0442(2001)014<0853:AOICDE>2.0.CO;2
(  0) 0) |
| [9] |
明锋, 杨元喜, 曾安敏. 共模误差PCA与ICA提取方法的比较[J]. 大地测量与地球动力学, 2017, 37(4): 385-389 (Ming Feng, Yang Yuanxi, Zeng Anmin. Comparison of PCA and ICA Extraction Methods for Common Mode Error[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 385-389)
(  0) 0) |
| [10] |
Tripathi S, Govindaraju R S. Engaging Uncertainty in Hydrologic Data Sets Using Principal Component Analysis: BaNPCA Algorithm[J]. Water Resour Res, 2008, 44: 1-15
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

