连续的GNSS坐标序列为大地测量学及地球动力学研究提供了宝贵的基础数据,被广泛应用于地壳运动状态监测、地震预测等领域。然而GNSS坐标序列中不仅存在线性变化,而且存在非线性运动,垂直方向尤为明显。一般认为,非线性变化是由技术系统误差、非构造形变以及随机因素(噪声)3个部分组成[1]。噪声和非构造形变使GNSS坐标序列产生较大的误差,无法获得真实的形变位移[2-3]。多位学者通过EMD以及EEMD法对时间序列进行处理,有效分离出了线性趋势项、周期项和噪声,能降低噪声并且估计形变速率[4-6]。然而EMD方法因存在模态混叠问题使得分解出来的序列物理意义不明确,分解的噪声层中含有少量的有效信息,直接除去会导致去噪后的数据精度降低,影响进一步的分析。
为了获得更为真实的GNSS垂向形变信息,本文提出利用ICEEMDAN法与最小二乘法对GNSS垂向序列进行噪声和非构造形变去除。拟采用一种改进的自适应噪声的ICEEMDAN方法对GNSS垂向序列进行分解,获得年周期项、半年周期项和趋势项,通过与小波变换以及经验模态分解等方法进行对比分析,择优选择GNSS垂向序列处理方法;对于GNSS垂向序列中的噪声,使用改进的小波阈值和排列熵值方法进行去噪重构处理;在去除噪声的基础上,通过与GNSS垂向序列中非构造形变的最小二乘数学模型拟合序列进行对比,获得真实的形变信息。
1 研究数据及研究方法 1.1 研究数据去除GNSS垂向序列噪声与非构造形变时,要求数据具有长时间的连续性,站点具有一定的分布性。基于以上考虑,选取中国大陆构造环境监测网络(COMONOC)6个站点(BJFS、BJSH、DLHA、LUZH、QION、YANC)1999~2013年的垂向序列进行分析。受地质灾害以及人为因素等影响,GNSS站点的位置时间序列难免会出现跃阶现象,如BJFS和BJSH站受日本仙台地震影响,QION站受2004年苏门答腊地震影响,LUZH站受2008年汶川地震影响等,都产生了不同程度的跃阶。在进行时间序列分析前要对出现的跃阶项进行修正,并剔除个别粗差点。图 1为6个GNSS站点的垂向序列,可以看出,GNSS垂向序列存在噪声,结合文献[2-3]提到的非构造形变,它们影响了GNSS垂向序列的进一步分析。因此,有必要对GNSS垂向序列开展噪声和非构造形变去除研究。

|
图 1 GNSS垂向序列 Fig. 1 Vertical time series of GNSS stations |
EMD算法假设时间序列可分解为若干有限的本征模态函数IMF和一个趋势项,趋势项代表该序列的变化趋势。EMD方法直观、简单,而且具有完备性、近似正交性、IMF分量的调制性以及良好的自适应性。但该方法存在着模态混叠的问题,模态混叠不仅导致信号的时频分布特性的混淆,还会使IMF分量的物理意义变得不明确[5]。为了解决该问题,许多学者提出EEMD、CEEMD等改进方法,但效果仍有待提高。
ICEEMDAN方法[7]的基本思想是在原始信号中加入EMD分解后的白噪声,再对每个混合信号进行EMD分解,利用每个信号的模态分量求平均得到剩余量,再解算模态分量,直到满足算法自身的停止准则。该方法在极大程度上解决了EMD分解后造成的模态混叠,以及会得到“虚假”的模态分量等问题。
GNSS坐标序列受到多种因素影响,其中GNSS观测得到的地壳形变通常包含有构造形变与非构造形变两类信息[2]。认知非构造形变对GNSS形变结果的影响,有必要探寻消除和修正非构造形变的方法。非构造形变对GNSS垂向序列的修正主要体现在年周期项上,对于半年周期项的修正幅度较小[8]。本文利用最小二乘法实现非构造形变序列的拟合,从而获得GNSS垂向序列的非构造形变特征[9]。
2 GNSS垂向序列分解方法选取对选取的6个站点的GNSS垂向序列分别用小波变换、EMD、EEMD以及ICEEMDAN方法分解并进行比对,其中小波变换的小波基函数为db8。为了研究不同比例白噪声对IMF分量的影响,EEMD法和ICEEMDAN法中加入的白噪声与原始信号的标准差之比分别取0.1、0.2、0.4[10]。
6个GNSS站点经过各个方法分解后可获得不同尺度的垂向坐标序列。由于篇幅原因,只列出由不同分解方法得到的BJFS站的年周期项、半年周期项和趋势项,并进行比对。
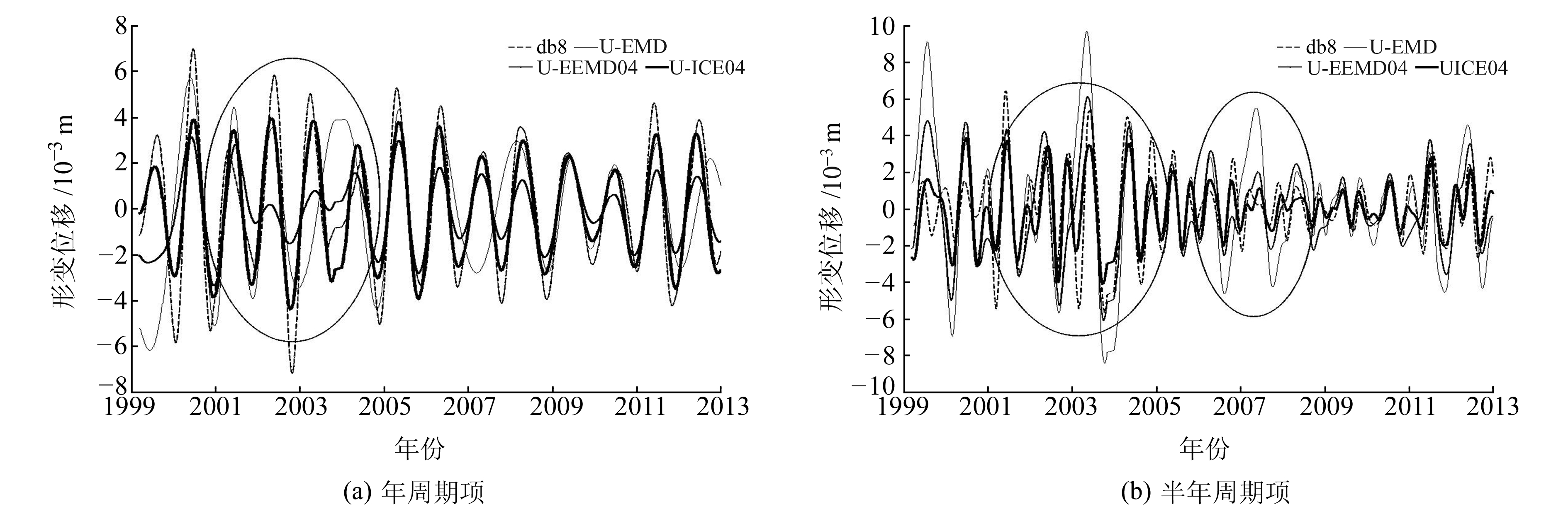
由图 2圆框处可看出,EEMD法和EMD法获得的年周期项在2003年附近的时间段存在明显的模态混叠现象;当标准差为0.1时,ICEEMDAN法也存在模态混叠现象,标准差为0.2和0.4时效果较好;和小波变换得到的年周期项相比,ICEEMDAN法曲线更加平滑,周期性更加明显,拟合效果更好。在半年周期项结果中,EEMD法和EMD法在2003年附近的时间段内周期为年周期,并不是半年周期,且EMD法分解后的序列在2007年附近表现异常,存在模态混叠现象。
|
图 2 BJFS站不同方法的年周期项与半年周期项对比 Fig. 2 Comparison of the anniversary and half-anniversary of BJFS station based on different methods |
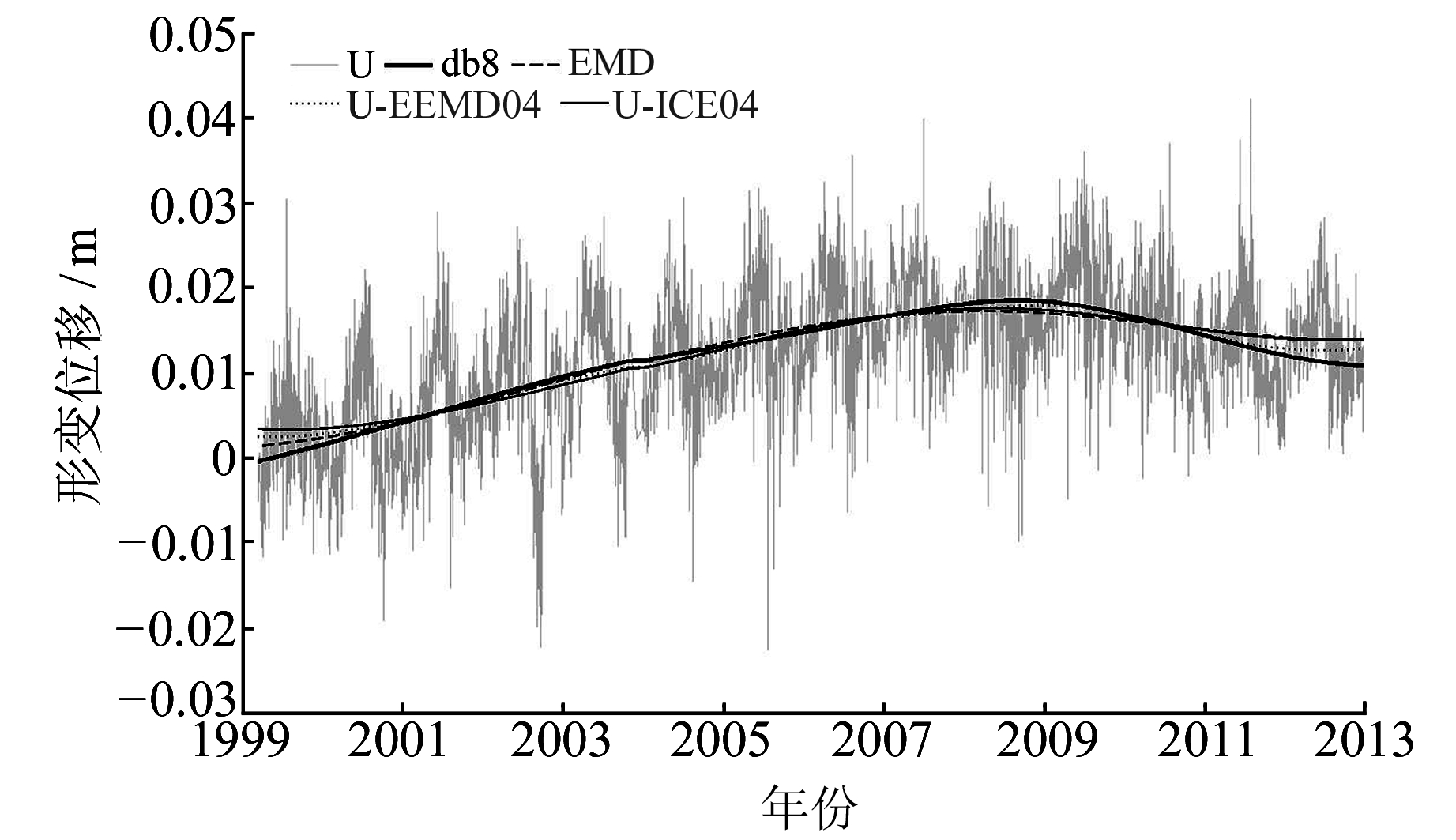
由图 3可知,各分解方法提取的趋势项与原始序列基本一致。BJFS站在1999~2009年高程方向有逐渐增高的趋势,并且上升速率在逐渐减小;2009~2013年呈缓慢下降的趋势,下沉速率逐渐减小。
|
图 3 BJFS站不同方法的趋势项对比 Fig. 3 Comparison of trend in different methods of BJFS station |
彭葳等[6]和Colominas等[7]分别通过互相关系数和Hurst指数获得分解后各个层数的值来确定噪声层数并直接去除。由于垂向序列的复杂性以及序列分解方法存在的计算问题,高频信号中也可能包含有效信息,因此不能直接去除。本文首先通过一种时间序列指标计算方法(排列熵算法(PE))计算分解后各分量的PE值,区分噪声层和非噪声层。以PE的值等于0.6为准,大于或等于0.6为噪声序列,小于0.6为真实形变序列,或者依据噪声层与非噪声层的PE值之间有一个较为明显的变化来进行分层;然后对噪声层使用一种改进的小波包阈值去噪方法[11]进行去噪,将去噪后的序列和非噪声层进行重构,从而获得去噪后的垂向序列。
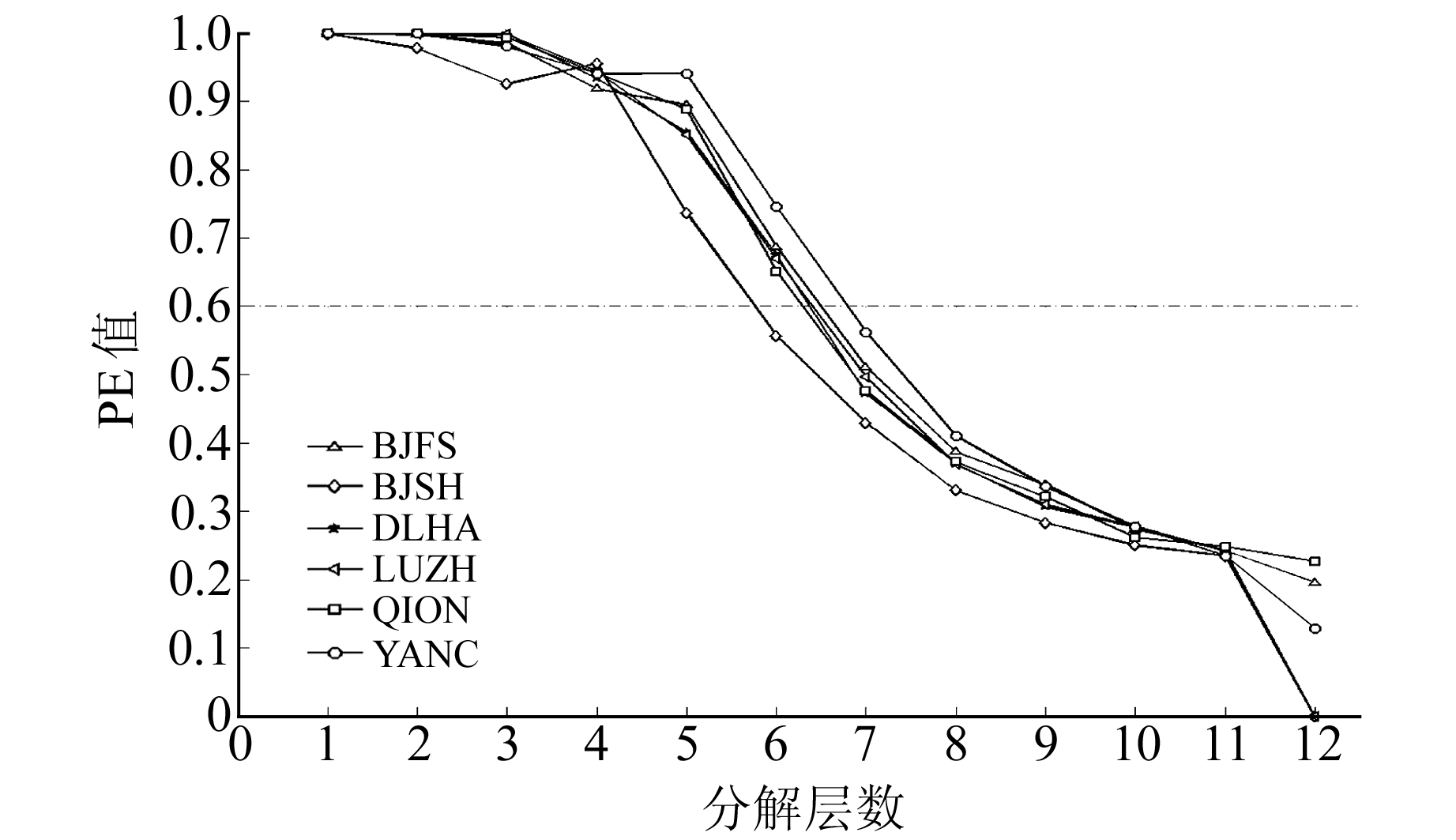
图 4是通过标准差为0.4的ICEEMDAN法对6个GNSS站点垂向序列分解后各个层数对应的排列熵值。
|
图 4 各站点对应层数的排列熵值 Fig. 4 The PE values of each layer of each station |
根据图 4,应将前6层作为噪声层进行去噪处理。为评定不同分解方法的去噪效果,各序列分解方法对应的信噪比值见表 1,信噪比越小说明去噪效果越好。
|
|
表 1 各序列分解方法对应的信噪比值 Tab. 1 The values of SNR corresponding to each series decomposition method |
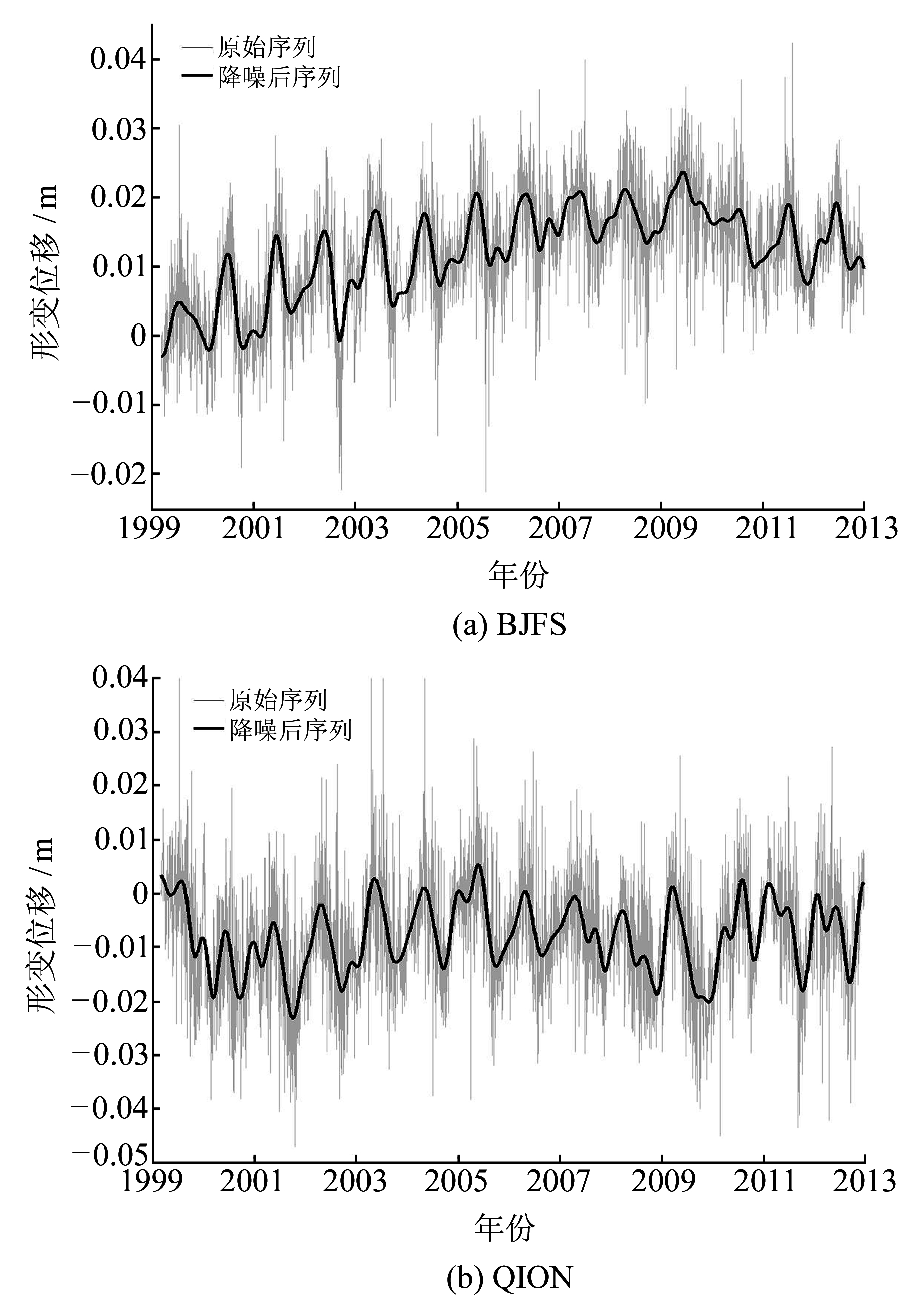
由表 1可知,本文采取的去噪方法的效果普遍优于其他方法;标准差为0.4时,ICEEMDAN法相比于其他的序列分析方法去噪效果更好。两种去噪方法对比中,虽然本文提出的方法有改进,但改进效果不明显,说明噪声层面中的有效信息较小,并且基于标准差为0.4时的ICEEMDAN法时,两种去噪方法的差距最小,说明噪声层面含有的有效信息最少,能很好地解决经验模态分解中的模态混叠问题。由于篇幅原因,只列出去噪后的两个站点的序列图(图 5)。可以看出,使用该方法去噪后得到的垂向序列能很好地反映GNSS垂向序列的位移变化,整体趋势更为清晰。
|
图 5 降噪前后GNSS垂向序列对比 Fig. 5 Comparison of GNSS vertical time series before and after noise reduction |
通过最小二乘法可拟合出GNSS垂向序列的非构造形变特征。在此只列出最小二乘法拟合的两个GNSS站点的非构造形变以及提取年周期项和年周期项加半年周期项3种时间序列的结果,见图 6。
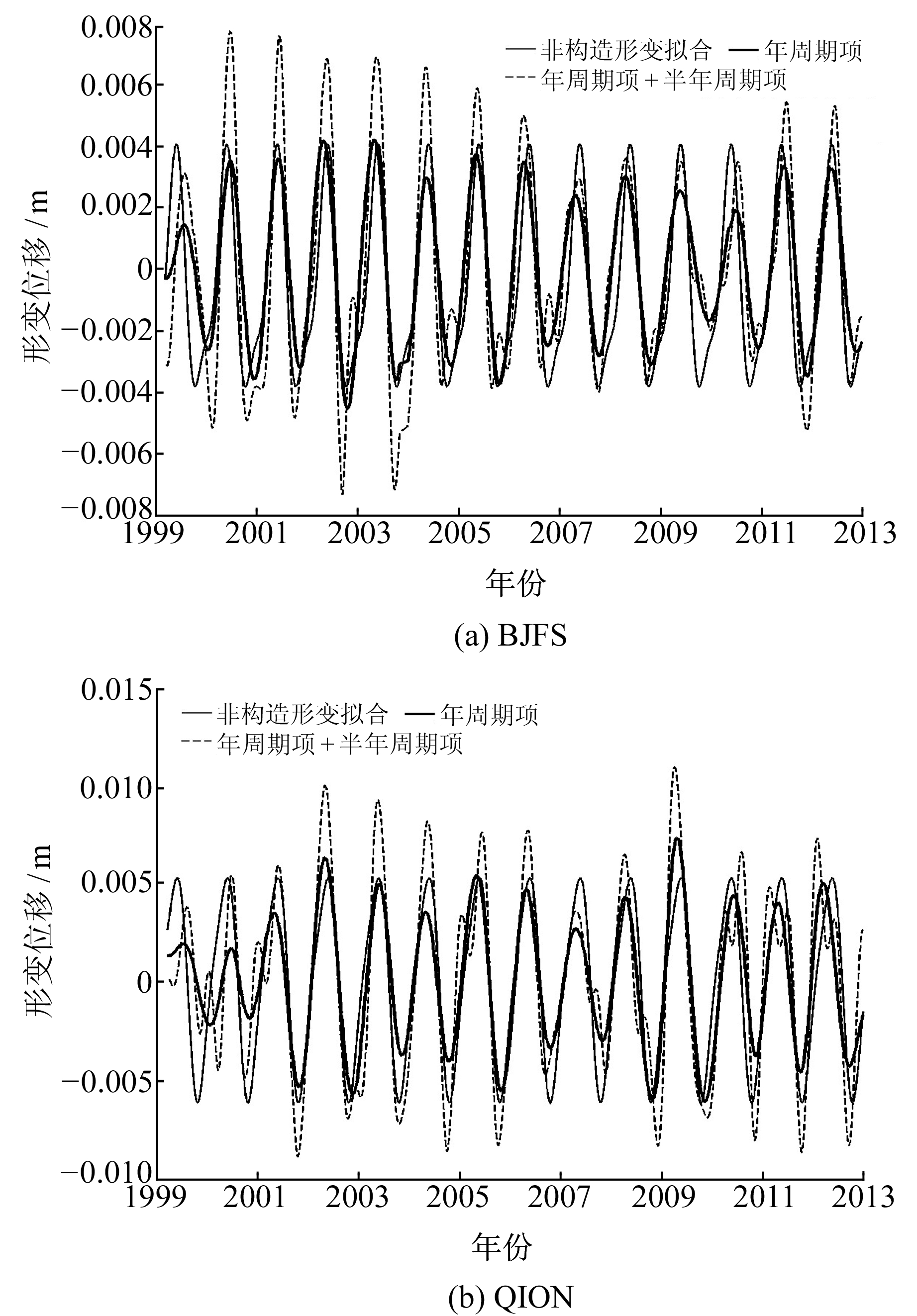
|
图 6 非构造形变序列对比 Fig. 6 Comparison of non-tectonic deformation series |
由图 6可以看出,年周期项序列和非构造形变序列最为接近。采用相关系数法计算6个站点年周期项以及年周期项加半年周期项与非构造形变序列的相关性,结果如表 2所示。
|
|
表 2 年周期项和年周期项+半年周期项与非构造形变序列的相关系数 Tab. 2 Correlation coefficient obtained by comparison with non-tectonic deformation sequences |
由表 2和图 6可知,年周期项序列和通过最小二乘法得到的非构造形变序列最为接近,半年周期项加年周期项的序列与非构造形变序列相差较大。并且由前文可知,非构造形变的修正结果对半年周期项的改正幅度很小,因此只选择年周期项的序列作为非构造形变序列进行修正。年周期项与得到的非构造形变序列仍存在一定的差异,主要是因为:1)地球物理效应引起的季节性变化可能不能很好地表现为正弦函数的形式;2)通过最小二乘法拟合的非构造形变序列虽然能得到形变特征及周期趋势,但在振幅方面过于模型化,与真实非构造形变位移有些差距。故将经过标准差为0.4的ICEEMDAN法分解后得到的年周期项作为非构造形变对去噪后的垂向序列加以修正,得到最终的结果。修正后序列的结果如图 7所示。

|
图 7 去除噪声和非构造形变的垂向序列与原始序列的对比 Fig. 7 Comparison of vertical series for noise removal and non-structural deformation and original series |
由图 7可见,经过修正后的垂向序列结果在振幅变化方面与原始序列相比降低了许多,并且能够反映形变的趋势。通过均方根(RMS)以及加权均方根(WRMS)差值[11]这一指标来衡量改正前后GNSS垂向序列的精度。本文研究与姜卫平等[12]研究的GNSS站点及垂向序列长度一致,两种方法计算的WRMS差值以及RMS值具有一定的可比性,计算后结果对比见表 3。
|
|
表 3 GNSS站点的WRMS差值和RMS值 Tab. 3 WRMS difference and RMS values of GNSS stations |
由表 3可知,RMS的值相较于姜卫平等[12]的结果普遍较小,可能是因为非构造形变中的大气荷载以及非海洋潮汐负荷对时间序列的影响大致呈现白噪声特征[13],在去噪阶段已经对其进行了处理,故RMS值较小;本文研究方法获得的WRMS差值高于姜卫平等[12]的研究结果,可能是因为姜卫平等[12]提取的环境负载序列并不能解释时间序列中全部的年周期项和半年周期项运动,而本文方法则将年周期项全部提出并去除,使得改正前后时间序列差值较大,故WRMS差值较大,改正效果较好。
5 结语本文对COMONC网络6个站点的垂向时间序列通过ICEEMDAN法进行处理,并与其他方法进行对比,然后进行去噪处理以及非构造形变的去除,获得以下结论:
1) ICEEMDAN法在GNSS垂向时间序列分析方面具有显著优势,可改进模态混叠问题,能正确地分离出年周期项、半年周期项以及趋势项。
2) 通过不同的去噪策略表明,噪声层中还含有少量的有效信息,并且通过ICEEMDAN法分解后直接去除噪声层和对噪声层进行去噪重构两种策略相差最小,进一步说明该方法对垂向时间序列的有效性。经过综合考虑,当标准差为0.4时,通过ICEEMDAN法对GNSS垂向时间序列进行分析能得到更好的结果。
3) 年周期项与最小二乘法拟合的非构造形变最为接近,可以直接进行改正;除QION站点外的RMS值普遍减小,平均为1.28 mm;除BJSH站点以外的WRMS值均有增大,平均为0.33 mm,改正效果明显。
致谢: 感谢中国地震局第一监测中心提供GNSS站点坐标时间序列。
| [1] |
钱闯, 刘晖, 丁志刚, 等. 顾及非构造形变的参考站长期稳定性分析[J]. 武汉大学学报:信息科学版, 2015, 40(9): 1 259-1 265 (Qian Chuang, Liu Hui, Ding Zhigang, et al. Long-Term Stability of Reference Stations by Taking Non-Tectonic Deformation into Account[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1 259-1 265)
(  0) 0) |
| [2] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1 045-1 052 (Wang Min, Shen Zhengkang, Dong Danan, et al. Effects of Non-Tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1 045-1 052)
(  0) 0) |
| [3] |
黄立人, 符养. GPS连续观测站的噪声分析[J]. 地震学报, 2007, 29(2): 197-202 (Huang Liren, Fu Yang. Analysis on the Noises from Continuously Monitoring GPS Sites[J]. Acta Seismologica Sinica, 2007, 29(2): 197-202 DOI:10.3321/j.issn:0253-3782.2007.02.009)
(  0) 0) |
| [4] |
张恒璟, 程鹏飞. 基于经验模式分解的CORS站高程时间序列分析[J]. 大地测量与地球动力学, 2012, 32(3): 129-134 (Zhang Hengjing, Cheng Pengfei. Analysis on Time Series of Two CORS Stations' Height Based on EMD[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 129-134)
(  0) 0) |
| [5] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1 248-1 252 (Zhang Shuangcheng, He Yuefan, Li Zhenyu, et al. EMD for Noise Reduction of GPS Time Series[J]. Journal of Geodesy and Geodynamics, 2017, 37(12): 1 248-1 252)
(  0) 0) |
| [6] |
彭葳, 戴吾蛟. 基于EEMD和Husrt指数的GNSS基准站的垂向速率估计[J]. 测绘工程, 2016, 25(4): 60-65 (Peng Wei, Dai Wujiao. Vertical Velocity Estimation of GNSS Reference Station Based on EEMD Method and Hurst Exponent[J]. Engineering of Surveying and Mapping, 2016, 25(4): 60-65 DOI:10.3969/j.issn.1006-7949.2016.04.014)
(  0) 0) |
| [7] |
Colominas M A, Schlotthauer G, Torres M E. Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing[J]. Biomedical Signal Processing and Control, 2014, 14: 19-29 DOI:10.1016/j.bspc.2014.06.009
(  0) 0) |
| [8] |
梁洪宝, 刘志广, 黄立人, 等. 非构造形变对中国大陆GNSS基准站垂向周期运动的影响[J]. 大地测量与地球动力学, 2015, 35(4): 589-593 (Liang Hongbao, Liu Zhiguang, Huang Liren, et al. Effects of Non-Tectonic Deformation on the Vertical Periodic Motion of GNSS Reference Stations in China[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 589-593)
(  0) 0) |
| [9] |
盛传贞.中国大陆非构造负荷地壳形变的区域性特征与改正模型[D].北京: 中国地震局地质研究所, 2013 (Sheng Chuanzhen. Characteristics of Non-Tectonic Crustal Deformation from Surface Loads around Chinese Mainland and Correction Model[D]. Beijing: Institute of Geology, CEA, 2013) http://www.cqvip.com/QK/92674X/201411/663324895.html
(  0) 0) |
| [10] |
施闯, 牛玉娇, 魏娜, 等. HHT-EEMD用于IGS站高程时间序列分析[J]. 大地测量与地球动力学, 2018, 38(7): 661-667 (Shi Chuang, Niu Yujiao, Wei Na, et al. Application of the HHT-EEMD Approach in Analysis of IGS Height Time Series[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 661-667)
(  0) 0) |
| [11] |
吴浩, 曹庭泉, 花向红, 等. GNSS时间序列中随机漫步消噪的改进半软阈值算法及其评估[J]. 测绘学报, 2016, 45(增2): 22-30 (Wu Hao, Cao Tingquan, Hua Xianghong, et al. An Improved Semisoft Threshold Algorithm and Its Evaluation for Denoising Random Walk in GNSS Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 22-30)
(  0) 0) |
| [12] |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014, 43(12): 1 217-1 223 (Jiang Weiping, Xia Chuanyi, Li Zhao, et al. Analysis of Environmental Loading Effects on Regional GPS Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1 217-1 223)
(  0) 0) |
| [13] |
贺小星. GPS台站时间序列分析及其地壳形变应用[D].南昌: 东华理工大学, 2013 (He Xiaoxing. Time Series Analysis of GPS Station and Its Application in Crustal Deformation[D]. Nanchang: East China University of Technology, 2013) http://cdmd.cnki.com.cn/Article/CDMD-10405-1013045663.htm
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

