2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
对建筑物进行长期观测所得到的变形监测数据,包含有真值和噪声(误差)两个部分,受仪器自身精度、周围环境中温度和湿度以及人为操作等因素的影响,噪声和真值会互相叠加在一起,使数据出现波动,因此有必要对变形监测数据进行去噪处理。如何有效地消除噪声,关系到建筑物变形预测的准确性。小波变换具有良好的时频特性,能够较好地反映信号的局部特征,被广泛应用于变形分析中[1-7]。影响小波去噪效果的因素有小波基的选择、阈值大小、分解层数以及阈值函数等几种。许多学者通过改进小波阈值函数和小波阈值,并应用到各种信号的去噪当中,都取得了良好的效果。本文基于众多学者的研究,提出一种新的小波阈值去噪函数。实验表明,新的小波阈值去噪函数对变形监测数据的去噪效果良好,在实际应用中有较大的发展前景。
1 小波阈值函数和阈值估计 1.1 传统阈值函数在小波去噪中,阈值函数的选择是一个关键问题,最常用的有软阈值函数和硬阈值函数,但这两种传统的阈值函数都存在缺陷。为此,很多学者对传统阈值函数进行优化和改进,提出各种改进的小波阈值去噪函数,取得了不错的效果。
软阈值函数的表达式为:
| $ \omega_{j, k}=\left\{\begin{array}{ll} {\operatorname{sign}(\omega)(|\omega|-T), } & {|\omega| \geqslant T} \\ {0, |\omega|<T} \end{array}\right. $ | (1) |
硬阈值函数的表达式为:
| $ \omega_{j, k}=\left\{\begin{array}{l} {\omega, |\omega| \geqslant T} \\ {0, |\omega|<T} \end{array}\right. $ | (2) |
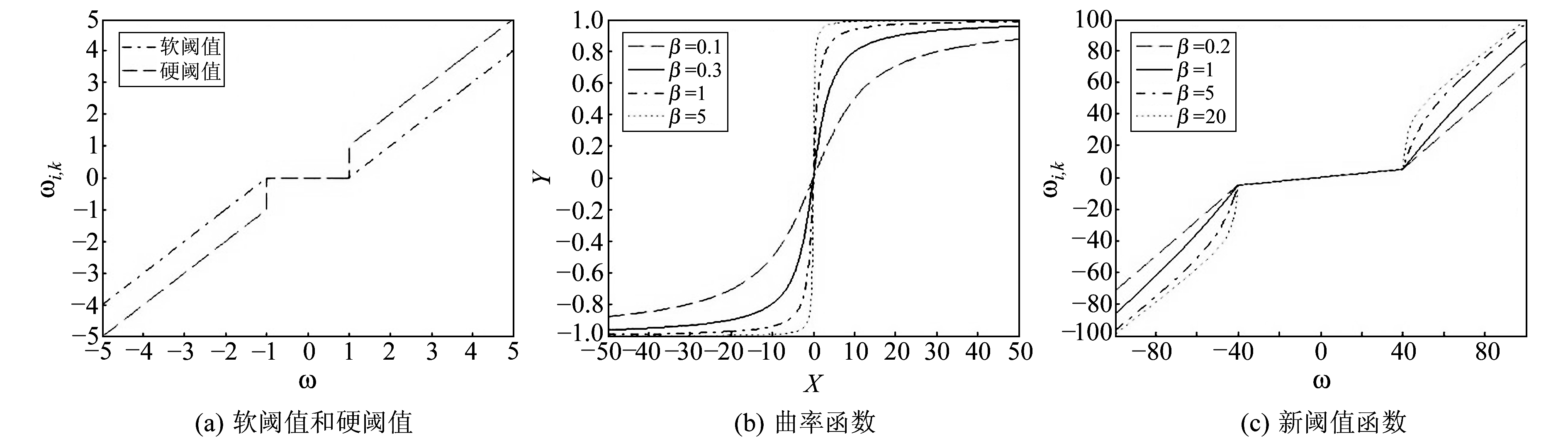
式中,ωj, k为去噪后输出的小波系数,ω为原始的小波系数,T为阈值向量。软阈值函数去噪后的小波系数与真实的小波系数之间存在着恒定的偏差T,会导致重构时信号精度降低、失真严重。而硬阈值函数由于在T和-T处的不连续性,导致重构后的信号可能出现不必要的震荡,即“伪吉布斯”现象。图 1(a)为硬阈值函数和软阈值函数的图像。
|
图 1 阈值函数 Fig. 1 Threshold function |
在小波阈值去噪中,阈值选取太大,会将部分有用的信号去除,引起偏差;若阈值选取太小,则导致信号去噪不完全。目前,最常用的阈值选取方法有通用阈值、自适应阈值、启发式阈值和极大极小阈值4种方法[8]。
1) 通用阈值:
| $ T=\sigma \sqrt{2 \ln (n)} $ | (3) |
式中,n为小波系数的个数,σ为噪声的方差,T为阈值向量。
2) 无偏风险原理的自适应阈值:
| $ T=\sigma \sqrt{\omega_{O}} $ | (4) |
式中,ωO为小波序列的平方向量,σ为噪声的方差。
3) 启发性原理的阈值估计:
设z为n个小波系数平方和,令x=(z-n)/n,y=(log2n)
| $ T=\left\{\begin{array}{l} {T_{1}, x \leqslant y} \\ {\min \left(T_{1}, T_{2}\right), x>y} \end{array}\right. $ | (5) |
4) 极大极小原理的阈值估计:
| $ T=\left\{\begin{array}{l} {\sigma\left(0.3936+0.1829 \log _{2} n\right), n>32} \\ {0, n \leqslant 32} \end{array}\right. $ | (6) |
式中,σ为噪声的方差,n为小波系数的个数。
从公式(3)~(6)可以看出,当小波分解的某一层信号中含有的噪声较多时,计算得到的阈值会变得较大。虽然噪声被全部去除,但信号系数小于阈值的部分也会被当成噪声去除,造成有用信号的缺失,出现失真现象,引起偏差。当小波分解的某一层信号中含有的噪声较少时,计算得到的阈值也会变小,这样噪声系数大于阈值的部分会保留下来,不能完全去除噪声,去噪的效果不理想。小波分解的每一层小波系数都有一个较为合适的阈值向量,因此,选取合适的阈值计算方法十分重要。为了能够准确地对变形监测数据进行去噪处理,本文采用了赵瑞珍等[4]基于通用阈值公式
| $ T=\frac{\sigma \sqrt{2 \log (N)}}{\log (j+1)} $ | (7) |
式中,σ2为噪声的标准差,N为各层采样信号系数的长度,j为小波的分解尺度。可以看出,随着小波分解尺度的变大,计算得到的阈值会逐渐减小,每一个分解尺度上选择的阈值都不相同,具有良好的自适应性,去噪效果更好。
在实际过程中,由于噪声的强度是未知的,因此不能运用噪声的标准差来直接计算噪声的大小,否则会影响信号去噪的精度。一般采用文献[3]中的噪声计算公式来计算噪声的大小:
| $ \sigma=\frac{1}{0.674} \frac{1}{N} \sum\limits_{K=1}^{N}|\omega| $ | (8) |
为克服软阈值函数的恒定偏差问题和硬阈值函数的不连续性,许多学者基于传统的阈值函数提出各种改进阈值函数,其中文献[4]提出的改进阈值函数为:
| $ \omega_{j, k}=\left\{\begin{array}{l} {\operatorname{sign}(\omega) \sqrt{\omega^{2}-T^{2}}, |\omega| \geqslant T} \\ {0, |\omega|<T} \end{array}\right. $ | (9) |
式中,ωj, k为去噪后输出的小波系数,ω为原始的小波系数,T为阈值向量。
文献[5]提出的改进阈值函数为:
| $ \omega_{j, k}=\left\{\begin{array}{ll} {\operatorname{sign}(\omega)} {\sqrt[j]{\omega^{j}-T^{j}}, |\omega| \geqslant T} \\ {0, |\omega|<T} \end{array}\right. $ | (10) |
式中,ωj, k为去噪后输出的小波系数,ω为原始的小波系数,T为阈值向量,j为分解尺度。
文献[6]提出的改进阈值函数为:
| $ \omega_{j \cdot k}=\left\{\begin{array}{l} {\omega-T \cdot \sin (\omega / T \cdot \pi / 2), |\omega| \geqslant T} \\ {0, |\omega|<T} \end{array}\right. $ | (11) |
式中,ωj, k为去噪后输出的小波系数,ω为原始的小波系数,T为阈值向量。
以上3种改进的小波阈值去噪函数都是在软阈值函数基础上改进而成,在一定程度上解决了恒定偏差问题,而且能保持软阈值函数的连续性,克服硬阈值函数存在的不连续性问题,去噪效果优于传统的阈值函数。但3种改进的阈值函数在|ω| < T处都是直接置零,这样会把部分真实信号也一并消除,去噪效果会产生一定的偏差。本文基于一种曲率函数,提出一种改进的小波阈值函数,这种曲率函数为:
| $ y=\frac{2}{\pi} \arctan (\beta x), \beta \in R $ | (12) |
该函数的变量x为X轴上的任何实数,而变量y为Y轴上[-1, 1]之间的任何实数。这个曲率函数是关于零对称的,可以通过参数β进行调整,图 1(b)显示了当参数β分别为0.1、0.3、1和5时的曲率函数图像。
基于上述曲率函数,本文提出的小波阈值函数为:
| $ V=\left\{\begin{array}{l} {\omega-T, \omega \geqslant T} \\ {\omega+T, \omega \leqslant-T} \end{array}\right. $ | (13) |
| $ \left\{\begin{array}{l} {V+\frac{2}{\pi} \arctan \left(\beta \frac{V}{T}+\operatorname{sign}(\omega) \alpha\right) T, |\omega| \geqslant T} \\ {\lambda \omega, |\omega|<T} \\ {0<\alpha<1, \beta>0, \lambda \in(0.05, 0.2)} \end{array}\right. $ | (14) |
式中,参数α用于实现不同程度的收缩率对高频系数的影响。在传统的硬阈值函数和软阈值函数当中,对于那些绝对值小于T的小波系数,总会被视为噪声并设置为零,这样将不可避免地会删除掉一些有用的信息,导致重构后的信号出现细节缺陷。在新的阈值函数中,小波的去噪过程通过引入3个参数而变得更加合理。当|ω|<T时,小波系数里面大部分是噪声,但是还有一小部分是有用的信号,去噪后的小波系数通过选择合适的参数λ来进行调整,而不是像以前的小波函数一样直接置零,但是要保证λ的值足够小,否则无法有效消除噪声。经算例表明,当λ∈(0.05, 0.2)时的效果较好[7];当|ω|≥T时,通过调整曲率函数中的参数β来改变去噪的过程,β→0时,去噪过程相当于软阈值函数,而β→∞时,去噪过程相当于硬阈值函数。图 1(c)显示了新阈值函数在不同参数的曲率函数下的变化图像,参数β的取值为0.2、1、5和20,阈值T取值为40,参数α取值为0.2。
1.4 去噪流程本次实验的去噪流程如图 2所示。

|
图 2 去噪流程 Fig. 2 Denoising flowchart |
为了验证本文阈值函数去噪的有效性,首先使用Matlab平台进行仿真实验。模拟一组变形监测数据的仿真信号S,信号S由长度为1 000、3个振幅频率不同的周期项和1个趋势项组成,步长设置为0.01,仿真信号S的表达式为[9]:
| $ \begin{array}{c} S = 3\sin (2\pi t/500){e^{ - t/1000}} + 2\sin (2\pi t/200) + \\ 2\sin (2\pi t/50) + t/1000 \end{array} $ | (15) |
变形监测数据中含有的噪声以白噪声为主,实验采用Matlab中自带的awgn函数为仿真信号S添加信噪比为db20的高斯白噪声,仿真信号S和仿真噪声信号S1如图 3所示。

|
图 3 仿真数据 Fig. 3 Simulation data |
使用6种小波阈值函数分别对仿真噪声信号S1进行去噪处理,采用分解能力较好的sym8小波基,分解层数选择为3。在本文阈值函数中,当α=0.2、β=5、λ=0.12时,去噪的效果良好(图 4)。

|
图 4 6种阈值函数的去噪效果 Fig. 4 Denoising effects of six threshold function |
从去噪的曲线看,6种去噪方法的区别不大。这是由于添加的高斯白噪声过于单一,容易被去除的缘故,因此需要从评价指标中进一步判断本文阈值函数去噪的有效性和可行性。
小波去噪的评价指标主要有信噪比、均方根误差和平滑度3种[10],本文用这3种评价指标对去噪效果进行对比分析。
信噪比指的是原始信号和噪声之间能量的比值,记为SNR,表达式为:
| $ {\rm{SNR}} = {\rm{10}} \times {\rm{l}}{{\rm{g}}_{10}}\left( {\frac{{\sum\limits_i^n {f_i^2} }}{{\sum\limits_i^n {{{({f_i} - {y_i})}^2}} }}} \right) $ | (16) |
式中,fi为去噪后的信号,yi为原始信号,n为信号长度。SNR值越大,去噪效果越好。
均方根误差指的是原始信号与去噪信号方差的平方根,主要体现出它们之间的差异,记为MSE,表达式为:
| $ {\rm{MSE}} = \sqrt {\frac{1}{n}\sum\limits_i^n {{{({f_i} - {y_i})}^2}} } $ | (17) |
式中,fi为去噪后的信号,yi为原始信号,n为信号长度。MSE值越小,去噪效果越好。
平滑度指的是去噪后信号的光滑度,即去噪信号和原始信号差分数的方差根之比,表达式为:
| $ R = \frac{{\sum\limits_{i = 1}^{n - 1} {{{[{f_1}(i + 1) - {f_1}(i)]}^2}} }}{{\sum\limits_{i = 1}^{n - 1} {{{[f(i + 1) - f(i)]}^2}} }} $ | (18) |
式中,f1(i)为去噪后的信号,f(i)为原始信号,n为信号长度。一般认为,信号越光滑,平滑度的指标越小,信号去噪的效果越好。但实际中由于信号过于光滑会去掉很多有用的信号,而且在真值未知的情况下平滑度没有极值,所以平滑度只能作为辅助的评价指标。表 1为6种阈值函数去噪后的评价指标。
|
|
表 1 6种阈值函数的去噪指标 Tab. 1 Denoising indicators of six threshold functions |
从表 1可知,软阈值去噪曲线除了平滑度占优外,信噪比最小,均方根误差最大,去噪效果较差。硬阈值去噪曲线由于不连续性,出现了部分震荡现象,导致平滑度最大,去噪曲线比较粗糙。其他3种改进的小波阈值去噪曲线与传统的阈值去噪曲线相比,克服了硬阈值函数的不连续性,一定程度上解决了软阈值函数存在的恒定偏差问题,去噪效果有了部分提升。本文阈值去噪曲线的信噪比最大,均方根误差最小,平滑度较小,与其他阈值去噪方法对比,效果要明显一些,说明本文阈值去噪算法是可行的。由于仿真实验添加的高斯白噪声过于单一,而变形监测数据含有的噪声较为复杂,因此需要从工程实例中进一步验证本文阈值函数去噪的有效性和可行性。
3 实例分析为进一步验证本文阈值函数去噪的可行性和有效性,本文对文献[11]中的某江岸有断裂的危岩上H监测点10 a的沉降监测数据进行实例分析,该信号如图 5所示。

|
图 5 监测点H的沉降监测变化曲线 Fig. 5 Subsidence monitoring curves at point H |
从图 5可以看出,该危岩H点的高程随着时间的增加呈现出下降的趋势。由于各种不确定的因素,该信号含有很多毛刺,严重影响到了变形监测的准确分析和预测,因此需要对其进行去噪处理。
使用6种小波阈值函数分别对该信号进行去噪处理。实验采用分解能力较好的sym8小波基,分解层数选为3。在本文阈值函数中,当α=0.2、β=5、λ=0.12时去噪的效果良好,去噪结果如图 6所示。

|
图 6 6种阈值函数的去噪效果 Fig. 6 Denoising effects of six threshold functions |
从图 6可以看出,软阈值函数去噪后的曲线太过平滑,失去了很多有用的信息。这是由于软阈值函数存在的恒定偏差问题,导致了重构后的信号失真比较严重。硬阈值函数去噪后的曲线在时间60~70月和时间110~120月附近出现的震荡现象比较严重,这是因为硬阈值函数在阈值处不连续而导致,即“伪吉布斯”现象。文献[4]阈值去噪后的曲线在时间60~70月处的震荡也比较严重,去噪效果较差。文献[5]和文献[6]阈值去噪后的曲线比较光滑,震荡不明显,从曲线上观察区别不大。本文阈值方法去噪后的曲线在时间60~100月之间的细节更加明显,曲线光滑,比其他阈值去噪方法的效果要明显一些。至于时间0~60月之间的曲线变化,6种阈值函数去噪的效果相差不大,需要从评价指标中进一步验证本文阈值函数去噪的有效性和可行性。表 2为6种阈值函数去噪后的评价指标。
|
|
表 2 6种阈值函数的去噪指标 Tab. 2 Denoising indicators of six threshold functions |
从表 2可知,软阈值去噪法除了平滑度占优外,均方根误差最大,信噪比最小,去噪的效果比较差,这是由于软阈值函数存在的恒定偏差问题,导致曲线的失真比较严重。硬阈值去噪法的信噪比不是很高,均方根误差比较大,由于不连续性,出现了很多震荡现象,导致平滑度最大,曲线较为粗糙,去噪效果较差。文献[4]和文献[5]阈值去噪法效果较好,均方根误差、信噪比以及平滑度相差不大。文献[6]阈值去噪方法信噪比较小,均方根误差较大,去噪效果不是很好,还可以继续进行优化和改进。本文阈值去噪方法的信噪比最大,均方根误差最小,平滑度较小,去噪的效果比其他阈值去噪方法更加明显,进一步说明本文阈值函数对变形监测数据的去噪是可行的。
结合图像分析和去噪评价指标的对比,本文阈值去噪法去噪后的曲线光滑,细节明显。与其他阈值去噪方法相比,信噪比有了较明显的提升,均方根误差和平滑度均有下降,说明本文阈值去噪方法是可行的,在变形监测数据处理方面有较大的参考价值。
4 结语本文通过构建新的小波阈值去噪函数,对模拟的仿真数据和真实的变形监测数据进行去噪处理,结果表明,新的小波阈值函数在一定程度上克服了软阈值函数存在恒定偏差、硬阈值函数不连续性的问题,重构后的信号细节更加明显,能够体现出建筑物变形的周期性变化,更加接近真实的变形情况,更好地反映了建筑物的变形规律,为后期的变形预测和分析提供了有效的参考。新阈值函数的去噪效果比传统的阈值算法和其他学者提出的阈值算法效果要明显,信噪比有较大的提升,均方根误差和平滑度均有所下降,在今后变形监测数据的处理中有较好的发展前景。
| [1] |
党星海, 赵丽洁, 孔令杰, 等. 小波分析在GPS振动监测数据中的应用[J]. 大地测量与地球动力学, 2013, 33(2): 147-150 (Dang Xinghai, Zhao Lijie, Kong Lingjie, et al. Application of Wavelet Analysis in GPS Vibration Monitoring Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 147-150)
(  0) 0) |
| [2] |
Donoho D L. De-Noising by Soft-Thresholding[J]. IEEE Translations on Information Theory, 1995, 41(3): 613-627 DOI:10.1109/18.382009
(  0) 0) |
| [3] |
Donoho D L, Johnstone J M. Ideal Spatial Adaptation by Wavelet Shrinkage[J]. Biometika, 1994, 81(2): 425-455
(  0) 0) |
| [4] |
赵瑞珍, 宋国乡, 王红. 小波系数阈值估计的改进模型[J]. 西北工业大学学报, 2001, 19(4): 625-628 (Zhao Ruizhen, Song Guoxiang, Wang Hong. Improved Model of Wavelet Coefficient Threshold Estimation[J]. Journal of Northwestern Polytechnical University, 2001, 19(4): 625-628 DOI:10.3969/j.issn.1000-2758.2001.04.031)
(  0) 0) |
| [5] |
朱伟华, 安伟, 尤丽华, 等. 基于改进阈值函数的小波阈值去噪算法[J]. 计算机系统应用, 2016, 25(6): 191-195 (Zhu Weihua, An Wei, You Lihua, et al. Wavelet Threshold Denoising Algorithm Based on Improved Threshold Function[J]. Computer Systems Applications, 2016, 25(6): 191-195)
(  0) 0) |
| [6] |
鲁道阳, 王泽民. 改进的小波阈值去噪算法研究[J]. 国外电子测量技术, 2018(2): 40-43 (Lu Daoyang, Wang Zemin. Research on Improved Wavelet Threshold Denoising Algorithm[J]. Foreign Electronic Measurement Technology, 2018(2): 40-43)
(  0) 0) |
| [7] |
易清明, 陈明敏, 石敏. 一种改进的小波去噪方法在红外图像中应用[J]. 计算机工程与应用, 2016, 52(1): 173-177 (Yi Qingming, Chen Mingmin, Shi Min. An Improved Wavelet Denoising Method for Infrared Image Application[J]. Computer Engineering & Applications, 2016, 52(1): 173-177 DOI:10.3778/j.issn.1002-8331.1401-0082)
(  0) 0) |
| [8] |
翟振兴.基于小波变换的信号去噪研究[D].重庆: 重庆大学, 2010 (Zhai Zhenxing. Signal Denoising Based on Wavelet Transform[D]. Chongqing: Chongqing University, 2010)) http://www.cnki.com.cn/Article/CJFDTotal-XALD200403016.htm
(  0) 0) |
| [9] |
罗甘, 梁月吉, 黄仪邦. 基于双树复小波的变形监测数据去噪分析[J]. 大地测量与地球动力学, 2018, 38(9): 82-87 (Luo Gan, Liang Yueji, Huang Yibang. Denoising Analysis of Deformation Monitoring Data Based on Double-Tree Complex Wavelet[J]. Journal of Geodesy and Geodynamics, 2018, 38(9): 82-87)
(  0) 0) |
| [10] |
陶珂.小波去噪质量评价方法研究[D].长沙: 中南大学, 2012 (Tao Ke. Research on Wavelet Denoising Quality Evaluation Method[D]. Changsha: Central South University, 2012) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2199960
(  0) 0) |
| [11] |
文鸿雁.基于小波理论的变形分析模型研究[D].武汉: 武汉大学, 2004 (Wen Hongyan. Research on Deformation Analysis Model Based on Wavelet Theory[D]. Wuhan: Wuhan University, 2004) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb200502018
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2020, Vol. 40
2020, Vol. 40


