形变观测数据不仅存在趋势变化,还存在非线性变化。低频趋势变化主要反映区域构造应力场控制下的继承性构造运动,而非线性变化主要受大气负载、地下水负载、非潮汐海洋负载、地表温度及地壳基岩的热胀冷缩等地球物理效应的共同作用[1-2]。大多数形变观测数据都呈现出显著的非线性运动趋势,尤其是季节变化带来的周期成分,主要表现为年周期震荡运动。此外,有些台站受观测环境变化、观测场地改造、仪器升级更换及构造运动等的影响,导致观测数据年周期形态发生改变,给年周期的正常拟合和去除带来困难。
在季节性信号提取的研究中,比较常用的年变拟合方法有最小二乘拟合、多项式拟合及傅里叶拟合周期分析等。最小二乘拟合是一种传统的经典拟合方法,常应用于GPS时间序列的拟合[3];傅里叶拟合是基于傅里叶变换的谐波拟合方法,对给定的频率可正确地拟合与其有关的谐波函数,最小二乘拟合和傅里叶拟合都是可以对固定周期进行拟合的方法。奇异谱分析是近年较热门的时间序列处理方法,可较好地从含噪声的有限尺度的时间序列中提取趋势和周期等信息[4-6],但传统奇异谱分析方法具有相移现象,不能有效分析不同形式的地球物理效应造成的非线性变化[7]。本文从实际应用角度出发,在介绍方法模型的基础上,分别利用最小二乘拟合及傅里叶拟合对形变观测数据进行年周期拟合分析。针对实际观测数据振幅非均匀变化的情况[8-10],引入F检验方法进行分段最小二乘拟合;傅里叶拟合则采用3 a窗长的滑动拟合方式,并通过实际观测数据检验各方法的优劣及适用性。
1 年变探测方法 1.1 最小二乘拟合在GPS坐标序列时变模型解算中,最常用的是最小二乘拟合法。形变观测数据时间序列与GPS坐标序列具有相似性,同样可以用该方法进行序列拟合。其模型如下:
| $ \begin{aligned} y(t)=& y_{0}+v t_{i}+a \sin \left(2 \pi f t_{i}\right)+\\ & b \cos \left(2 \pi f t_{i}\right)+\varepsilon\left(t_{i}\right) \end{aligned} $ | (1) |
式中,ti为时间(单位d),y0为截距常数,v为线性速率,a、b为周期项系数,f为年周期对应的频率,ε(t)为噪声项。长度为n的观测序列模型用矩阵表示为:
| $ \boldsymbol{y}=\boldsymbol{A x}+\boldsymbol{e}, D(\boldsymbol{y})=\sigma_{0}^{2} \boldsymbol{P}^{-1} $ | (2) |
其中的系数矩阵和参数向量分别为:
| $ \left\{\begin{array}{ll} {\boldsymbol{A}=\left[\begin{array}{cccc} {1} & {t_{1}} & {\sin \left(2 \pi f t_{1}\right)} & {\cos \left(2 \pi f t_{1}\right)} \\ {1} & {t_{2}} & {\sin \left(2 \pi f t_{2}\right)} & {\cos \left(2 \pi f t_{2}\right)} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ {1} & {t_{n}} & {\sin \left(2 \pi f t_{n}\right)} & {\cos \left(2 \pi f t_{n}\right)} \end{array}\right]} \\ {\boldsymbol{x}=\left[\begin{array}{cccc} {y_{0}} & {v} & {a} & {b} \end{array}\right]^{{\rm T}}} \end{array}\right. $ | (3) |
假设观测序列的振幅在tk时刻发生变化,则该时刻前后需设置不同参数进行描述,即在tk时刻以后增加一组跟振幅有关的参数,系数矩阵和参数向量变为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{A}}_k} = \left[ {\begin{array}{*{20}{c}} 1&{{t_1}}&{\sin (2{\rm{ \mathsf{ π} }}f{t_1})}&{\cos (2{\rm{ \mathsf{ π} }}f{t_1})}&0&0\\ 1&{{t_2}}&{\sin (2{\rm{ \mathsf{ π} }}f{t_2})}&{\cos (2{\rm{ \mathsf{ π} }}f{t_2})}&0&0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&{{t_k}}&{\sin (2{\rm{ \mathsf{ π} }}f{t_k})}&{\cos (2{\rm{ \mathsf{ π} }}f{t_k})}&0&0\\ 1&{{t_{k + 1}}}&0&0&{\sin (2{\rm{ \mathsf{ π} }}f{t_{k + 1}})}&{\cos (2{\rm{ \mathsf{ π} }}f{t_{k + 1}})}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&{{t_n}}&0&0&{\sin (2{\rm{ \mathsf{ π} }}f{t_n})}&{\cos (2{\rm{ \mathsf{ π} }}f{t_n})} \end{array}} \right]\\ {\mathit{\boldsymbol{x}}_k} = {\left[ {\begin{array}{*{20}{c}} {{y_0}}&v&{{a_1}}&{{b_1}}&{{a_2}}&{{b_2}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (4) |
后验单位权方差估值为:
| $ {\mathit{\boldsymbol{\hat \sigma }}} _k^2 = \frac{{{{\left( {{\mathit{\boldsymbol{y}}} - {{\mathit{\boldsymbol{A}}}_k}{{{\mathit{\boldsymbol{\hat x}}}}_k}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}}\left( {{\mathit{\boldsymbol{y}}} - {{\mathit{\boldsymbol{A}}}_k}{{{\mathit{\boldsymbol{\hat x}}}}_k}} \right)}}{{n - {m_k}}} $ | (5) |
式中,mk为参数个数。
对观测序列振幅变化较大的点进行搜索。首先假设分段点k(k=2, 3, …, n-1)对应的方差为
| $ F = \frac{{{\mathit{\boldsymbol{\hat \sigma }}} _0^2}}{{{\mathit{\boldsymbol{\hat \sigma }}} _p^2}}\sim{F_\alpha }\left( {n - m, n - {m_p}} \right) $ | (6) |
根据经验数据显著水平α=0.2,单边检验中F≥Fα,表明分段点振幅变化显著。此时,将原数据时间序列分成2个区间,按照前述过程分别对2个区间进行新分段点搜索与显著性检验,直到找到所有的分段点[9]。
1.3 滑动傅里叶法滑动傅里叶法的原理[10]为:设观测数据的时间序列为{yn}(n=1, 2, …,N),N为有限长度,年变化周期为T,即1 a中有T个等时间间隔的年变化成分观测值,序列{x}={x1, x2, …, xN}为{y}中的年变化成分。使用三角级数公式,由序列{y}中的T个数据组成的长度为T的子序列{yn-T+1, yn-T+2, yn-T+3, …, yn}拟合出年变化成分(即基波)的第n个值xn,再由{yn-T+2, yn-T+3, yn-T+4, …, yn+1}拟合出xn+1,依此类推。年变化计算公式为:
| $ \begin{array}{c} {x_n} = {a_n}\cos \frac{{2{\rm{ \mathsf{ π} }}\left( {j - n + T} \right)}}{T} + \\ {b_n}\sin \frac{{2{\rm{ \mathsf{ π} }}\left( {j - n + T} \right)}}{T}\\ n = T, T + 1, \cdots , N;j = \\ n - T + 1, n - T + 2, \cdots , n \end{array} $ | (7) |
其中,
| $ {a_n} = \frac{2}{T}\sum\limits_{j = n - T + 1}^n {{y_i}\cos \frac{{2{\rm{ \mathsf{ π} }}\left( {j - n + T} \right)}}{T}} $ | (8a) |
| $ {b_n} = \frac{2}{T}\sum\limits_{j = n - T + 1}^n {{y_i}\sin \frac{{2{\rm{ \mathsf{ π} }}\left( {j - n + T} \right)}}{T}} $ | (8b) |
在具体操作过程中发现,由于每个台站测项年变形态差异较大,有些台站经历过改造或更换仪器等,再加上一些环境干扰和构造运动,年变振幅并非保持稳定不变。用傅氏滑动拟合标准年变时选取T=365为周期、3T为窗长进行滑动,可避免年变幅度异常造成的拟合结果的不稳定。
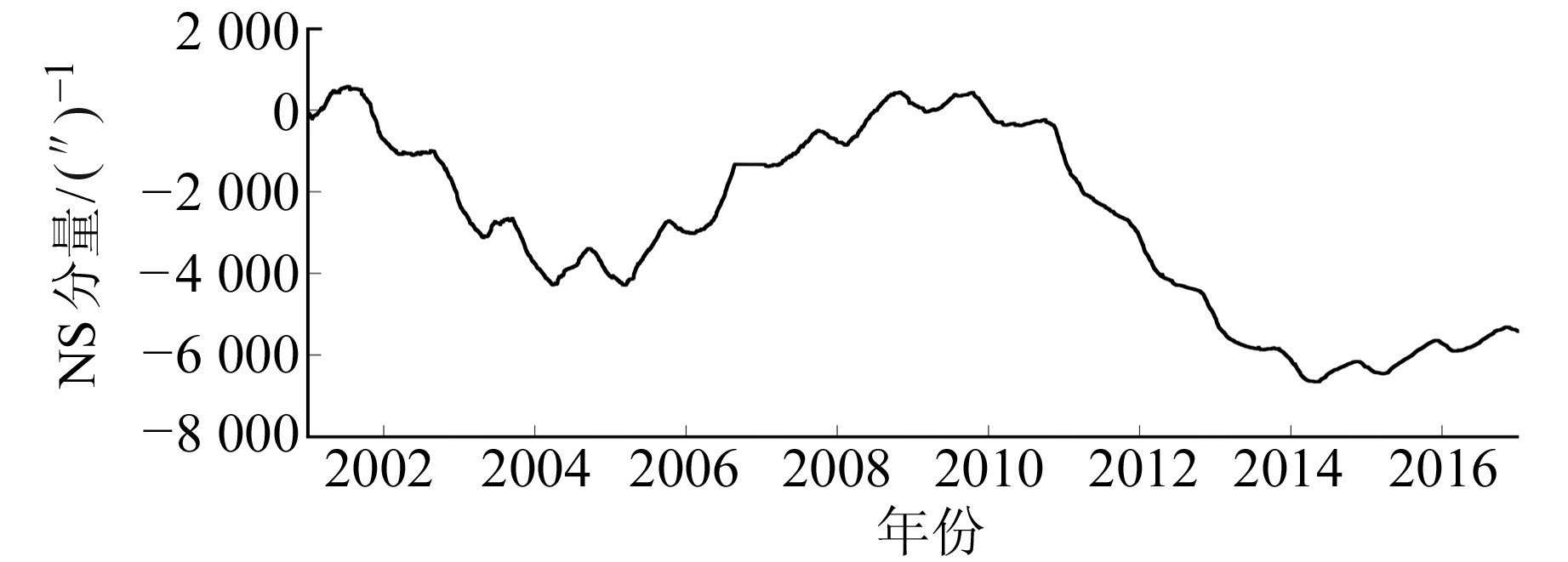
2 数据分析 2.1 原始数据预处理由于前兆数据的复杂性,观测数据包含复杂的周期成分,对年周期成分干扰较大,在数据处理之前需对原始数据进行预处理,包括数据质量检查、去除低频长期趋势项等,最终保留较“干净”的年周期成分。以库尔勒水平摆倾斜仪NS分量观测曲线为例(图 1),该仪器安置于霍拉山南坡山洞内,在构造上位于南天山褶皱带与塔里木地台的交界部位,山洞内有一条走向为NE-NEE的活动断裂,断裂上的元古界灰色黑云母片麻岩和大理岩逆冲于上新统砂砾岩层之上。洞内湿度小于80%,温度在15 ℃左右,年温差小于0.5 ℃,摆墩为预埋的整块花岗岩,用水泥与台基基岩粘合[11]。
|
图 1 库尔勒水平摆倾斜仪NS分量日值曲线 Fig. 1 The curve of daily observation of Korla horizontal pendulum tiltmeter |
从图 1可以看出,库尔勒水平摆倾斜仪NS分量2001~2017年曲线存在准5 a周期、1 a周期及高频波动。低频趋势变化明显,对1 a周期形态的拟合存在很大干扰,因此需对原始数据进行预处理。本文选用日值数据,利用小波9阶分解,去掉512 d以上周期的低频趋势项,保留约1.5 a以内尺度的周期成分。同时,顾及到年周期拟合不需要高频信息,滤波平滑了16 d以内的高频成分,得到比较“干净”的年周期变化曲线,为后续年周期拟合及年周期异常形态提取提供了有利条件。
2.2 变振幅年周期信号提取选取不同数据长度、不同年周期变化形态的3列地倾斜观测数据进行年周期拟合对比分析。温泉水平摆倾斜仪EW分量数据存在6个完整的年周期,年周期幅度变化较小,周期成分形态比较稳定,2015年底以来的年周期存在幅度变小的情况;库尔勒水平摆倾斜仪NS分量数据长度超过13 a,年周期振幅变化无明确规律,每年变化量均不相同,2004~2013年有一定的大小年现象,除此之外整段数据还存在相位改变的情况;精河水平摆倾斜仪EW分量数据长度达到24 a,观测数据的连续性和稳定性较高,年周期清晰,年周期振幅变化较平缓,年周期相位比较稳定,相位改变的情况少。
参与计算的3种方法均以365 d为周期,最小二乘法和分段最小二乘法中采用的频率即为1/365,滑动傅里叶法选取3T(T=365)作为窗长。分段最小二乘法通过F检验判断分段点的显著性,显著水平取经验数据α=0.2。当显著水平小于0.2时,数据前后变化较小的分段点不易找出。α的值可根据不同数据源进行调整。
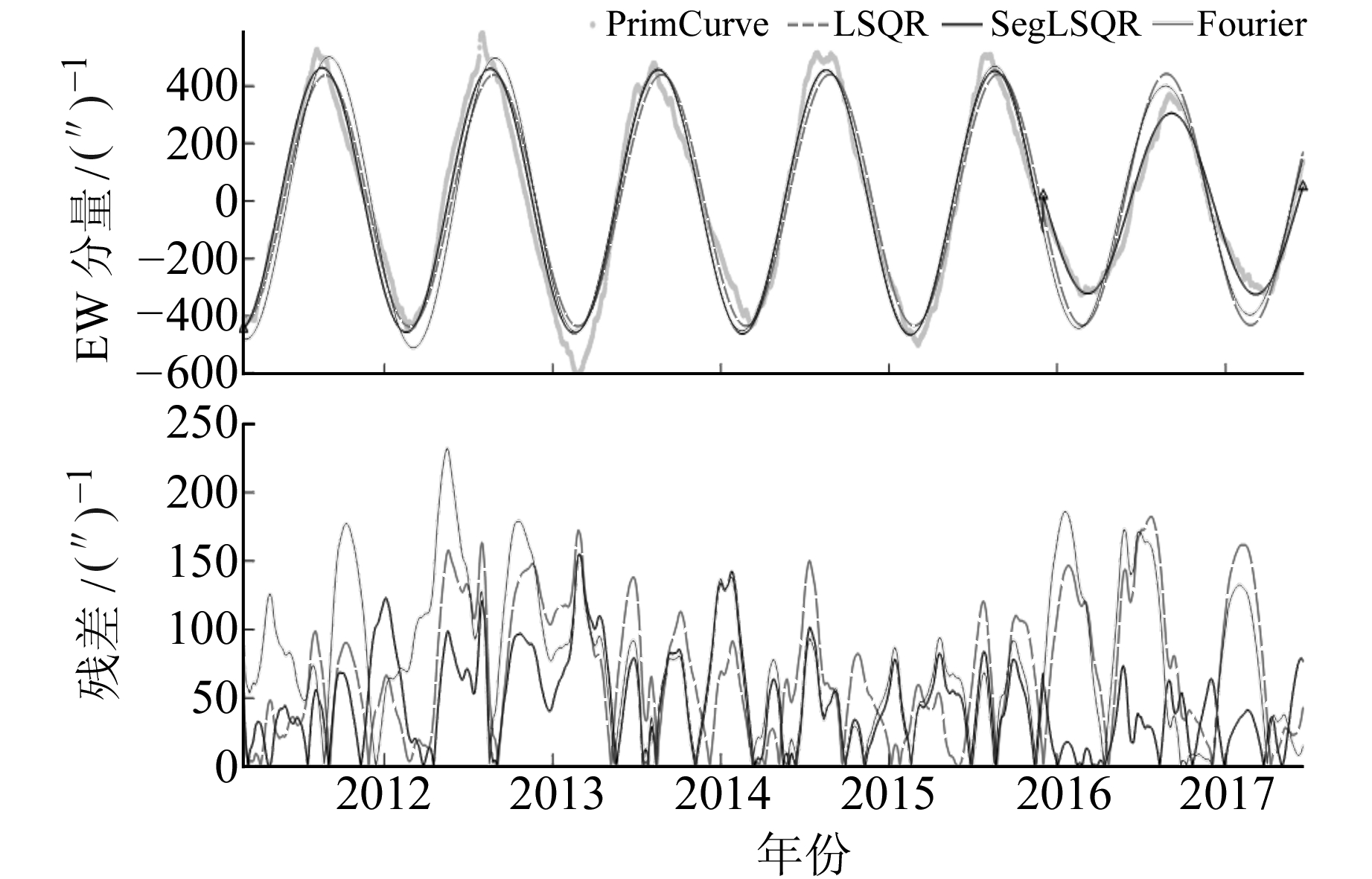
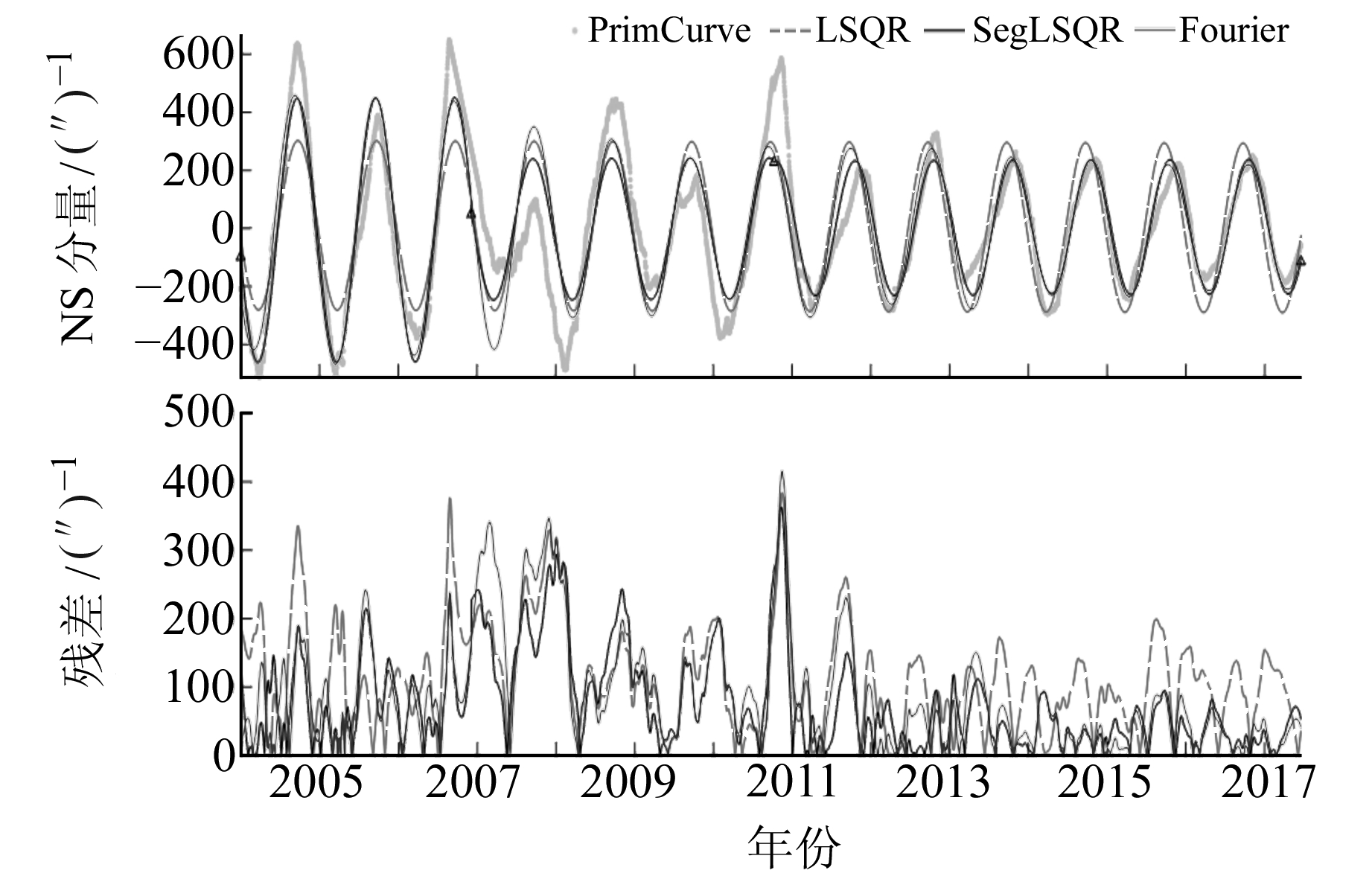
拟合结果见图 2~4,其中,灰色散点为预处理后的观测数据,虚线为最小二乘法拟合结果,黑色曲线为分段最小二乘法拟合结果,黑色三角为分段点,深灰色曲线为滑动傅里叶法拟合结果,图中各曲线为观测值与拟合值的残差绝对值曲线。由图 2可知,3种方法都能较好地拟合观测数据,且残差均小于100/(″),分段最小二乘法对振幅改变的周期进行了分段拟合,新的拟合周期成功拟合了相位改变后的数据,但也在分段点产生不连续台阶。图 3中的观测数据形态比较复杂,振幅变化频繁,每年都有振幅改变的情况且改变量正负交替。2006~2011年,3种方法的拟合残差都有所增加,非规律性的振幅改变很难用模型进行完美拟合。总的来说,分段最小二乘法拟合残差最小,拟合结果更接近观测数据。图 4中的观测数据长度超过20 a,年周期振幅经历多次改变,但不同于图 3每年改变一次振幅的情况,振幅的缓慢变化使得滑动傅里叶法能充分发挥模型优势,但限制了分段最小二乘法分段探测的敏感性,因此滑动傅里叶法拟合残差最小,分段最小二乘法与最小二乘法结果基本一致。
|
图 2 温泉水平摆倾斜仪EW分量拟合和残差曲线 Fig. 2 The fitting curves and theresiduals of Wenquan horizontal pendulum tiltmeter(EW) |
|
图 3 库尔勒水平摆倾斜仪NS分量拟合和残差曲线 Fig. 3 The fitting curves and theresiduals of Korla horizontal pendulum tiltmeter(NS) |

|
图 4 精河水平摆倾斜仪EW分量拟合和残差曲线 Fig. 4 The fitting curves and theresiduals of Jinghe horizontal pendulum tiltmeter(EW) |
由表 1可知,分段最小二乘法拟合结果标准差要优于其他两种方法,但当观测数据较长且年周期振幅缓慢变化时,分段最小二乘法无法进行分段,其结果与最小二乘法结果基本一致。因此,对于振幅变化的情况,滑动傅里叶法适用性更好一些。
|
|
表 1 3种方法拟合结果标准差 Tab. 1 The standard deviations of the three methods |
功率谱分析可找出时间序列中的优势频段,通过谱分析方法能够检验拟合残差中年频率谱是否仍然显著,从而判断年周期拟合的效果。图 5分别给出去趋势后的观测序列功率谱及3种方法拟合残差序列的功率谱。对于年周期365 d来说,其频率的对数为-2.6。由图 5(a)可明显看到,年频率的功率谱最大,说明观测序列中年周期显著存在。图 5(b)显示,年频率能量虽然不是最大值,但仍然较高,说明传统最小二乘拟合法没有完全去除年周期成分。图 5(c)和5(d)显示,年频率能量明显下降,说明分段最小二乘法和滑动傅里叶法拟合效果较好,年周期成分得以较成功地去除。

|
图 5 功率谱分析 Fig. 5 Spectrum analysis |
通过对3种方法年周期的拟合结果进行比较,可以看出:
1) 最小二乘法受模型限制,仅能拟合出固定振幅、固定相位的年周期信号,对年周期变化比较规律的曲线拟合程度高、残差小,但对变振幅年周期的拟合效果较差。
2) 基于F检验的分段最小二乘法,在最小二乘基础上增加分段点的自动搜索,可自适应振幅改变的情况。该方法既继承了最小二乘法的优点,又顾及到观测数据年周期形态的复杂多样性,从3个测项年周期拟合残差的标准差也能看出,该方法拟合效果最好。对于个别相位改变的年周期,分段最小二乘法也能较好地拟合出来,但分段点不连续,存在分段台阶或周期不连续现象。
3) 滑动傅里叶法在数据较长、振幅改变的情况下拟合效果最优。该方法可通过前3 a数据调整拟合参数,年周期振幅缓慢持续改变的拟合结果明显优于年周期振幅突变的拟合结果。与最小二乘法一样,滑动傅里叶法以365 d为拟合周期,且未考虑相位参数,因此对于相位改变的拟合结果与原始数据序列存在相位差。
目前常用的等振幅年周期拟合方法与变振幅滑动年周期拟合方法均存在一定局限性,对于历史资料变化较复杂的观测数据,如何更好、更合理地拟合年周期仍需进一步研究。
| [1] |
Dong D, Fang P, Bock Y, et al. Anatomy of Apparent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4)
(  0) 0) |
| [2] |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014, 43(12): 1217-1223 (Jiang Weiping, Xia Chuanyi, Li Zhao, et al. Analysis of Environmental Loading Effects on Regional GPS Coordinate Time Series[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1217-1223)
(  0) 0) |
| [3] |
Davis J L, Wernicke B P, Tamisiea M E. On Seasonal Signals in Geodetic Time Series[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B1)
(  0) 0) |
| [4] |
黄立人. GPS基准站坐标分量时间序列的噪声特征分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [5] |
江在森, 张希, 祝意青, 等. 昆仑山口西MS8.1级地震前区域构造变形背景[J]. 中国科学D辑, 2003, 33(增1): 163-172 (Jiang Zaisen, Zhang Xi, Zhu Yiqing, et al. Regional Tectonic Deformation Background before the MS8.1 Earthquake in the West of Kunlun Pass[J]. Science in China Series D, 2003, 33(S1): 163-172)
(  0) 0) |
| [6] |
王解先, 连丽珍, 沈云中. 奇异谱分析在GPS站坐标监测序列分析中的应用[J]. 同济大学学报:自然科学版, 2013, 41(2): 282-288 (Wang Jiexian, Lian Lizhen, Shen Yunzhong. Application of Singular Spectral Analysis to GPS Station Coordinate Monitoring Series[J]. Journal of Tongji University:Natural Science, 2013, 41(2): 282-288)
(  0) 0) |
| [7] |
张旺, 尹磊, 徐韶光, 等. 改进奇异谱分析方法的GPS时间序列分析[J]. 测绘科学, 2019, 44(3): 28-33 (Zhang Wang, Yin Lei, Xu Shaoguang, et al. An Improved Singular Spectrum Analysis Method for Analysis of GPS Time Series[J]. Science of Surveying and Mapping, 2019, 44(3): 28-33)
(  0) 0) |
| [8] |
卢辰龙, 匡翠林, 戴吾蛟, 等. 采用变系数回归模型提取GPS坐标序列季节性信号[J]. 大地测量与地球动力学, 2014, 34(5): 94-100 (Lu Chenlong, Kuang Cuilin, Dai Wujiao, et al. Extracting Seasonal Signals from Continuous GPS Time Series Based on Varying-Coefficient Regression Models[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 94-100)
(  0) 0) |
| [9] |
李伟伟, 沈云中. GNSS站坐标序列速度和振幅变化的探测与分析[J]. 同济大学学报:自然科学版, 2014, 42(4): 604-610 (Li Weiwei, Shen Yunzhong. Detection and Analysis of Velocity and Amplitude Changes in GNSS Coordinate Series[J]. Journal of Tongji University: Natural Science, 2014, 42(4): 604-610)
(  0) 0) |
| [10] |
杜学斌, 孙君嵩, 陈军营. 地震预测中的地电阻率数据处理方法[J]. 地震学报, 2017, 39(4): 531-548 (Du Xuebin, Sun Junsong, Chen Junying. Processing Methods for the Observation Data of Georesistivity in Earthquake Prediction[J]. Acta Seismologica Sinica, 2017, 39(4): 531-548)
(  0) 0) |
| [11] |
邢喜民, 张涛. 分段回归在剔除精河、库尔勒水平摆气象因素影响的探索[J]. 地震工程学报, 2015(2): 623-628 (Xing Ximin, Zhang Tao. Subsection Regression Method for Removing Meteorological Factors in the Jinghe, Korla Horizontal Pendulum[J]. China Earthquake Engineering Journal, 2015(2): 623-628)
(  0) 0) |
 2020, Vol. 40
2020, Vol. 40

