病态问题广泛存在于卫星定位、大地测量反演及重力场向下延拓等大地测量解算模型中，当病态模型的设计阵存在误差时，该模型即演变为病态总体最小二乘模型。目前，关于病态总体最小二乘模型的解算有众多方法，如截断奇异值法、正则化法、虚拟观测值解法及谱修正迭代法等。在大地测量的很多领域，利用参数间一些精确已知的先验约束信息可显著提高解的准确性和精度^[1]，因此在病态总体最小二乘问题中，附加正确的等式约束也应当能够提高其解的准确性和精度^[2-3]。本文通过建立等式约束病态总体最小二乘模型，给出约束病态总体最小二乘模型的正则化准则，根据拉格朗日极值法导出约束病态总体最小二乘模型的正则化解及其精度评定公式，并以数值算例和病态测边网算例验证公式的正确性。

1 病态总体最小二乘模型的正则化解

总体最小二乘问题的函数模型为:

$ \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}} = \left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{E}}_A}} \right)\mathit{\boldsymbol{X}} $

(1)

式中，L、e∈R^m分别为观测值及误差向量，A、E_A∈R^m×n分别为系数矩阵及误差矩阵，且rank(A)=n < m，X∈Rⁿ为待估参数。假设观测值和系数矩阵元素的权阵均为单位阵，则其随机模型为：

$ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{e}}\\ {{\mathit{\boldsymbol{e}}_A}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{e}}\\ {{\rm{vec}}\left( {{\mathit{\boldsymbol{E}}_A}} \right)} \end{array}} \right] \sim N\left( {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {\sigma _0^2{\mathit{\boldsymbol{I}}_m}}&{}\\ {}&{\sigma _0^2{\mathit{\boldsymbol{I}}_{m \times n}}} \end{array}} \right]} \right) $

(2)

式中，e_A= vec (E_A), vec(·)为矩阵向量化算子，σ₀为先验单位权中误差，I为单位阵。

根据总体最小二乘平差准则求解式(1), 得：

$ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e = e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} = \min $

(3)

当法矩阵N=A^TA病态时，由式(3)求得的总体最小二乘解不可靠。袁振超等^[4]基于Tikhonov正则化原理导出病态总体最小二乘模型的正则化解，引入正则化因子α, 构建如下的病态总体最小二乘正则化准则：

$ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e = e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} = \min $

(4)

根据准则构造拉格朗日极值函数：

$ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( {\mathit{\boldsymbol{e}},{\mathit{\boldsymbol{e}}_A},\lambda ,{\bf{X}}} \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} + \mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} + }\\ {2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{AX}} + {\mathit{\boldsymbol{E}}_A}\mathit{\boldsymbol{X}}} \right)} \end{array} $

(5)

式中，λ∈R^m为拉格朗日因子。将函数Φ分别对e、e_A、λ、X求偏导，并令其为0，可得病态总体最小二乘问题的正则化迭代解：

$ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + b{\mathit{\boldsymbol{I}}_n}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

(6)

式中，$b=\alpha\left(1+\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)-\frac{(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})^{\mathrm{T}}(\boldsymbol{L}-\boldsymbol{A} \boldsymbol{X})}{\left(1+\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)}$, 具体的迭代解算过程见文献[4]。

2 等式约束病态总体最小二乘模型 2.1 等式约束病态总体最小二乘模型的正则化解

考虑等式约束病态总体最小二乘模型：

$ \begin{array}{l} \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}}\left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{E}}_A}} \right)\mathit{\boldsymbol{X}}\\ \mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{K}}_0} \end{array} $

(7)

式中, K∈R^l×n为约束阵，且rank(K)=l < m，K₀∈R^l为约束常数项。根据式(4)并顾及等式约束条件构建拉格朗日函数：

$ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( {\mathit{\boldsymbol{e}},{\mathit{\boldsymbol{e}}_A},\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }},\mathit{\boldsymbol{X}}} \right) = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} + \mathit{\boldsymbol{e}}_A^{\rm{T}}{\mathit{\boldsymbol{e}}_A} + \alpha {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} + }\\ {2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{AX}} + {\mathit{\boldsymbol{E}}_A}\mathit{\boldsymbol{X}}} \right) + 2{\mathit{\boldsymbol{\mu }}^{\rm{T}}}\left( {\mathit{\boldsymbol{KX}} - {\mathit{\boldsymbol{K}}_0}} \right)} \end{array} $

(8)

式中，μ∈R^l为约束因子, E_AX=(X^T⊗I_m)·e_A, ⊗为Kronecker积算子。将式(8)分别对e、e_A、λ、μ、X求偏导，并令其为0, 得：

$ \frac{1}{2} \cdot \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{e}}}} = \mathit{\boldsymbol{\hat e}} - \mathit{\boldsymbol{\hat \lambda }} = 0 $

(9a)

$ \frac{1}{2} \cdot \frac{{\partial \mathit{\Phi }}}{{\partial {\mathit{\boldsymbol{e}}_A}}} = {{\mathit{\boldsymbol{\hat e}}}_A} + \left( {\mathit{\boldsymbol{\hat X}} \otimes {\mathit{\boldsymbol{I}}_m}} \right)\mathit{\boldsymbol{\hat \lambda }} = 0 $

(9b)

$ \frac{1}{2} \cdot \frac{{\partial \mathit{\Phi }}}{{\partial \lambda }} = \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{\hat e}} - \mathit{\boldsymbol{A\hat X}} + {{\mathit{\boldsymbol{\hat E}}}_A}\mathit{\boldsymbol{\hat X}} = 0 $

(9c)

$ \frac{1}{2} \cdot \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{\mu }}}} = \mathit{\boldsymbol{K\hat X}} - {\mathit{\boldsymbol{K}}_0} = 0 $

(9d)

$ \frac{1}{2} \cdot \frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{X}}}} = \alpha \mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} + \mathit{\boldsymbol{\hat E}}_A^{\rm{T}}\mathit{\boldsymbol{\hat \lambda }} + {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }} = 0 $

(9e)

由式(9a)和式(9b)得：

$ \mathit{\boldsymbol{\hat e}} = \mathit{\boldsymbol{\hat \lambda }},{{\mathit{\boldsymbol{\hat e}}}_A} = - \left( {\mathit{\boldsymbol{\hat X}} \otimes {\mathit{\boldsymbol{I}}_m}} \right)\mathit{\boldsymbol{\hat \lambda }},{{\mathit{\boldsymbol{\hat E}}}_A} = - \mathit{\boldsymbol{\hat \lambda }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}} $

(10)

将其代入式(9c)得：

$ \mathit{\boldsymbol{\hat \lambda }} = \left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)^{ - 1}} $

(11)

由式(9e)得：

$ - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} = - \mathit{\boldsymbol{\hat E}}_A^{\rm{T}}\mathit{\boldsymbol{\hat \lambda }} - {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }} - \alpha \mathit{\boldsymbol{\hat X}} $

(12)

根据式(10)~(12)可得：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A\hat X}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} = - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) = }\\ { - \mathit{\boldsymbol{\hat E}}_A^{\rm{T}}\mathit{\boldsymbol{\hat \lambda }}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) - {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) - }\\ {\alpha \mathit{\boldsymbol{\hat X}}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) = {{\mathit{\boldsymbol{\hat \lambda }}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)\mathit{\boldsymbol{\hat X}} - }\\ {{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) - \alpha \mathit{\boldsymbol{\hat X}}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) = }\\ {\mathit{\boldsymbol{\hat X}}v - {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) - \alpha \mathit{\boldsymbol{\hat X}}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)} \end{array} $

(13)

式(13)可改写为：

$ \begin{array}{*{20}{c}} {\left[ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \alpha \left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right){\mathit{\boldsymbol{I}}_n}} \right]\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} + }\\ {{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }}\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) = \mathit{\boldsymbol{\hat Xv}}} \end{array} $

(14)

式中，

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}} = {{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right){{\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}^{ - 1}} = }\\ {\left( {{{\mathit{\boldsymbol{\hat \lambda }}}^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }}} \right)\left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) = {{\mathit{\boldsymbol{\hat e}}}^{\rm{T}}}\mathit{\boldsymbol{\hat e}} + \mathit{\boldsymbol{\hat e}}_A^{\rm{T}}{{\mathit{\boldsymbol{\hat e}}}_A} = }\\ {\left[ {{\mathit{\boldsymbol{L}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right) - {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right)} \right]{{\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}^{ - 1}} = }\\ {\left[ {{\mathit{\boldsymbol{L}}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat X}}} \right) + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat Xv}}} \right]{{\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}^{ - 1}} - }\\ {{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{\hat \mu }} - \alpha {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \end{array} $

(15)

将式(15)两端同乘$\left(1+\hat{\boldsymbol{X}}^{\mathrm{T}} \hat{\boldsymbol{X}}\right)$并变形得：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}} - {{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\hat X}} - \mathit{\boldsymbol{K}}_0^{\rm{T}}\mathit{\boldsymbol{\hat \mu }}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right) - }\\ {\alpha {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)} \end{array} $

(16)

组合式(9d)、式(14)和式(16)，将其改写成矩阵形式得:

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \alpha \left( {1\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right){\mathit{\boldsymbol{I}}_n}}&{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}}&{{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}\\ {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{A}}}&{{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}} - \alpha {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}&{\mathit{\boldsymbol{K}}_0^{\rm{T}}\left( {1 + {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}} \right)}\\ \mathit{\boldsymbol{K}}&{{\mathit{\boldsymbol{K}}_0}}&{\hat v{\mathit{\boldsymbol{I}}_l}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ { - 1}\\ {\mathit{\boldsymbol{\hat \mu }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ { - 1}\\ {\mathit{\boldsymbol{\hat \mu }}} \end{array}} \right]\dot v $

(17)

可以看出，参数解即为最小特征值对应的特征向量的一部分。考虑到式(17)中系数阵及特征向量均存在参数，因此需要迭代求解，具体迭代步骤为：

1)  $i=0, \hat{\boldsymbol{X}}^{(0)}$取普通最小二乘解；

2)  $\hat{v}^{(i)}=\left(\boldsymbol{L}-\boldsymbol{A} \hat{\boldsymbol{X}}^{(i)}\right)^{\mathrm{T}}\left(\boldsymbol{L}-\boldsymbol{A} \hat{\bf{X}}^{(i)}\right)(1+\left.\left(\hat{\boldsymbol{X}}^{(i)}\right)^{\mathrm{T}} \hat{\boldsymbol{X}}^{(i)}\right)^{-1}$，$p^{(i)}=1+\left(\hat{\boldsymbol{X}}^{(i)}\right)^{\mathrm{T}} \hat{\boldsymbol{X}}^{(i)}$；

3)  $\left[\begin{array}{l}{\hat{\boldsymbol{X}}} \\ {\hat{\boldsymbol{\mu}}}\end{array}\right]^{(i+1)}=\left[\begin{array}{cc}{\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\alpha p^{(i)} \boldsymbol{I}_{n}} & {\boldsymbol{K}^{\mathrm{T}} p^{(i)}} \\ {\boldsymbol{K}} & {0}\end{array}\right]^{-1}\left[\begin{array}{c}{\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}+\hat{\boldsymbol{X}}^{(i)} \hat{v}^{(i)}} \\ {\boldsymbol{K}_{0}}\end{array}\right]$；

4)  当$\left\|\hat{\boldsymbol{X}}^{(i+1)}-\hat{\boldsymbol{X}}^{(i)}\right\| < \varepsilon$时，迭代结束；否则，令i=i+1，并转至第2)步。

本文导出的迭代公式同时考虑法矩阵的病态性、系数阵的误差及等式约束，当不考虑等式约束条件时，与文献[4]的公式等价；法矩阵良态即正则化因子α取0时，与文献[3]的公式等价。

2.2 约束正则化解的精度评定

病态总体最小二乘模型约束正则化解的单位权方差的计算式为^[3]：

$ \hat \sigma _0^2 = \frac{{{{\mathit{\boldsymbol{\hat e}}}^{\rm{T}}}\mathit{\boldsymbol{\hat e}} + \mathit{\boldsymbol{\hat e}}_A^{\rm{T}}{{\mathit{\boldsymbol{\hat e}}}_A}}}{{m - {\rm{rank}}\left( \mathit{\boldsymbol{A}} \right) + {\rm{rank}}\left( \mathit{\boldsymbol{K}} \right)}} = \frac{{\hat v}}{{m - n + l}} $

(18)

需要指出的是，由于非线性模型的影响及引入正则化因子破坏了观测方程的等式结构，所求的参数解及其残差均是有偏的，利用有偏残差估计的单位权方差显然也是有偏的，即根据式(18)获得的单位权方差是有偏的。沈云中等^[5]和Xu等^[6]分别使用2种方法导出病态方程正则化解的无偏单位权方差计算公式，但在附有等式约束的病态总体最小二乘问题中，由于参数需迭代求解，与观测量无法显示分离，加上设计阵本身也是随机量，其单位权方差无偏估计相当复杂。

将迭代步骤3)中的公式进行适当变换得：

$ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ {\mathit{\boldsymbol{\hat \mu }}} \end{array}} \right]}^{\left( {i + 1} \right)}} = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \left( {\alpha {p^{(i)}} - \hat v} \right){\mathit{\boldsymbol{I}}_n}}&{{\mathit{\boldsymbol{K}}^{\rm{T}}}{p^{\left( i \right)}}}\\ \mathit{\boldsymbol{K}}&0 \end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}}\\ {{\mathit{\boldsymbol{K}}_0}} \end{array}} \right]} \end{array} $

(19)

其中，$D\left\{\left[\begin{array}{c}{\boldsymbol{A}^{\mathrm{T}} \boldsymbol{L}} \\ {\boldsymbol{K}_{0}}\end{array}\right]\right\}=\hat{\sigma}_{0}^{2}\left[\begin{array}{cc}{\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}} & {0} \\ {0} & {0}\end{array}\right]$，根据协方差传播定律，参数的协方差矩阵为：

$ D\left\{ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}}\\ {\mathit{\boldsymbol{\hat \mu }}} \end{array}} \right]} \right\} \approx \hat \sigma _0^2\mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}}&0\\ 0&0 \end{array}} \right]{\mathit{\boldsymbol{B}}^{\rm{T}}} $

(20)

式中，$\boldsymbol{B}=\left[\begin{array}{cc}{\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+(\alpha p-\hat{v}) \boldsymbol{I}_{n}} & {\boldsymbol{K}^{\mathrm{T}} \boldsymbol{p}} \\ {\boldsymbol{K}} & {0}\end{array}\right]^{-1}$。根据分块矩阵求逆公式，式(20)的分块矩阵形式为：

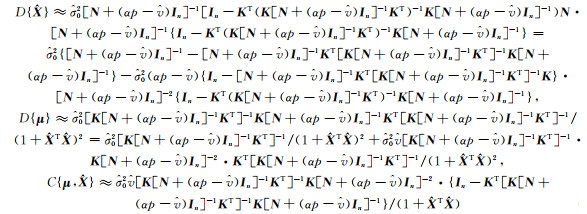
(21)

2.3 正则化参数的确定

本文采用与L曲线法类似的U曲线法^[7]来确定正则化参数α。L曲线法是根据不同的α值得到若干组$\|\boldsymbol{A} \hat{\boldsymbol{X}}-\boldsymbol{L}\|^{2}$和$\|\hat{\boldsymbol{X}}\|^{2}$值，并以$\|\boldsymbol{A} \hat{\boldsymbol{X}}-\boldsymbol{L}\|^{2}$为横坐标、$\|\hat{\boldsymbol{X}}\|^{2}$为纵坐标，经曲线拟合后得到的曲线上曲率最大的点对应的α即为所求的正则化参数。显然，L曲线法的精度受限于$\|\boldsymbol{A} \hat{\boldsymbol{X}}-\boldsymbol{L}\|^{2}$和$\|\hat{\boldsymbol{X}}\|^{2}$数据之间的拟合程度。

U曲线法与L曲线法类似，给定一组α, 计算U(α)为：

$ U\left( \alpha \right) = \frac{1}{{x\left( \alpha \right)}} + \frac{1}{{y\left( \alpha \right)}} = \frac{1}{{{{\left\| {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right\|}^2}}} + \frac{1}{{{{\left\| {\mathit{\boldsymbol{\hat X}}} \right\|}^2}}} $

(22)

式中，$\|{\boldsymbol{A}} \hat{\boldsymbol{X}}-{\boldsymbol{L}}\|^{2}=\sum\limits_{i=1}^{r} \frac{\alpha^{4} f_{i}^{2}}{\left(\lambda_{i}^{2}+\alpha\right)^{2}}$，$\|\hat{\boldsymbol{X}}\|^{2}=\sum\limits_{i=1}^{r} \frac{\lambda_{i}^{2} f_{i}^{2}}{\left(\lambda_{i}^{2}+\alpha\right)^{2}}$，f=U^TL，U为A经过奇异值分解后的左侧矩阵，λ₁≥λ₂≥…≥λ_r>0为A的r个从大到小排列的非零奇异值。所求的正则化参数即为曲线U(α)上曲率最大点对应的α^[8]，曲率的计算式为：

$ K = \frac{{\left| {{U^{\prime \prime }}(\alpha )} \right|}}{{{{\left[ {1 + {{\left( {{U^\prime }(\alpha )} \right)}^2}} \right]}^{3/2}}}} $

(23)

式中，U′(α)和U″(α)分别为U(α)的一阶导数和二阶导数，且

$ \begin{array}{l} {U^\prime }(\alpha ) = - \frac{{x'\left( \alpha \right)}}{{x{{\left( \alpha \right)}^2}}} - \frac{{y'\left( \alpha \right)}}{{y{{\left( \alpha \right)}^2}}},\\ {U^{\prime \prime }}(\alpha ) = {\left( {{U^\prime }(\alpha )} \right)^\prime } = \\ - \frac{{x\left( \alpha \right)x''\left( \alpha \right) - 2{{\left( {x'\left( \alpha \right)} \right)}^2}}}{{x{{\left( \alpha \right)}^3}}} - \\ \frac{{y\left( \alpha \right){y^{\prime \prime }}\left( \alpha \right) - 2{{\left( {{y^\prime }\left( \alpha \right)} \right)}^2}}}{{y{{\left( \alpha \right)}^3}}} \end{array} $

(24)

式中，x′(α)、x″(α)和y′(α)、y″(α)分别为x(α)和y(α)的一阶和二阶导数，其计算式见文献[9]。

3 算例与分析 3.1 数值算例

采用文献[10]中的算例1，该算例中有10个观测值和5个未知参数，其设计矩阵与观测值真值分别为：

$ \mathit{\boldsymbol{\tilde A = }}\left[ {\begin{array}{*{20}{c}} {2.00}&{ - 5.00}&{1.00}&{1.00}&{ - 9.50}\\ { - 2.00}&{4.00}&{1.00}&{ - 1.05}&{8.50}\\ { - 2.00}&{1.00}&{1.00}&{ - 1.00}&{2.40}\\ { - 1.00}&{2.50}&{4.00}&{ - 0.50}&{7.00}\\ { - 1.00}&{3.20}&{4.00}&{ - 0.50}&{8.40}\\ {1.00}&{1.00}&{ - 3.00}&{0.40}&{0.49}\\ {3.00}&{7.00}&{ - 3.00}&{1.50}&{12.70}\\ {5.00}&{ - 1.00}&{ - 2.00}&{2.50}&{ - 3.00}\\ {4.00}&{2.00}&{ - 2.00}&{2.00}&{5.00}\\ {4.00}&{3.00}&{ - 2.00}&{2.00}&{5.00} \end{array}} \right],\mathit{\boldsymbol{\tilde L}} = \left[ \begin{array}{l} - 10.50\\ 10.45\\ 1.40\\ 12.00\\ 14.10\\ - 0.11\\ 21.20\\ 1.50\\ 9.01\\ 12.00 \end{array} \right] $

参数真值$\tilde{\boldsymbol{X}}$=[1 1 1 1 1]^T。分别对观测真值$\tilde{\boldsymbol{L}}$和设计矩阵Ã模拟误差e和e_A, 其中e~N(0, σ₀²I₁₀), e_A=vec(E_A)~N(0, σ₀²I₁₀⊗I₅), σ₀为单位权中误差，取0.1，I为单位阵。

加入随机误差后的新设计矩阵和观测向量为^[10]：

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {1.8812}&{ - 5.1186}&{1.0129}&{1.0806}&{ - 9.5331}\\ { - 2.2202}&{3.8944}&{1.0656}&{ - 1.0268}&{8.4156}\\ { - 1.9014}&{1.1472}&{0.8832}&{ - 1.0990}&{2.4498}\\ { - 1.0519}&{2.5056}&{3.9539}&{ - 0.3660}&{7.1488}\\ { - 0.9673}&{3.0783}&{3.9738}&{ - 0.4710}&{8.3454}\\ {1.0234}&{0.9959}&{ - 3.1213}&{0.5479}&{0.4053}\\ {3.0021}&{6.8872}&{ - 3.1319}&{1.6138}&{12.6750}\\ {4.8996}&{ - 1.1349}&{ - 1.9069}&{2.4316}&{ - 2.9337}\\ {3.9053}&{1.9739}&{ - 1.9989}&{1.8808}&{2.9146}\\ {3.9626}&{3.0953}&{ - 2.0645}&{1.9927}&{4.8799} \end{array}} \right],\mathit{\boldsymbol{L}} = \left[ \begin{array}{l} - 10.5120\\ 10.4430\\ 1.4485\\ 11.9400\\ 14.0850\\ - 0.1535\\ 21.1920\\ 1.6535\\ 8.9454\\ 11.8650 \end{array} \right] $

法矩阵A^TA的条件数为2.083 7×10⁴，严重病态。分别使用最小二乘法(LS)、总体最小二乘法(TLS)、病态总体最小二乘正则化算法^[4](简称袁振超法)、混合正则化法^[10]、约束总体最小二乘法^[3](CTLS)和本文提出的约束病态总体最小二乘正则化算法进行解算，其中等式约束条件为：

$ {\mathit{\boldsymbol{X}}_i} + {\mathit{\boldsymbol{X}}_{i + 1}} = 2,i = 1,2,3,4 $

图 1为使用U曲线法确定正则化参数的示意图。比较不同算法获得的参数估值$\hat{\boldsymbol{X}}$与真值X的差值范数$\|\hat{\boldsymbol{X}}-\boldsymbol{X}\|$和相对偏差范数$\kappa=\|\hat{\boldsymbol{X}}-\boldsymbol{X}\| /\|\hat{\boldsymbol{X}}\|$‖，结果见表 1。表 2为参数估值的单位权方差及其方差-协方差阵估值。

3.2 病态测边网算例

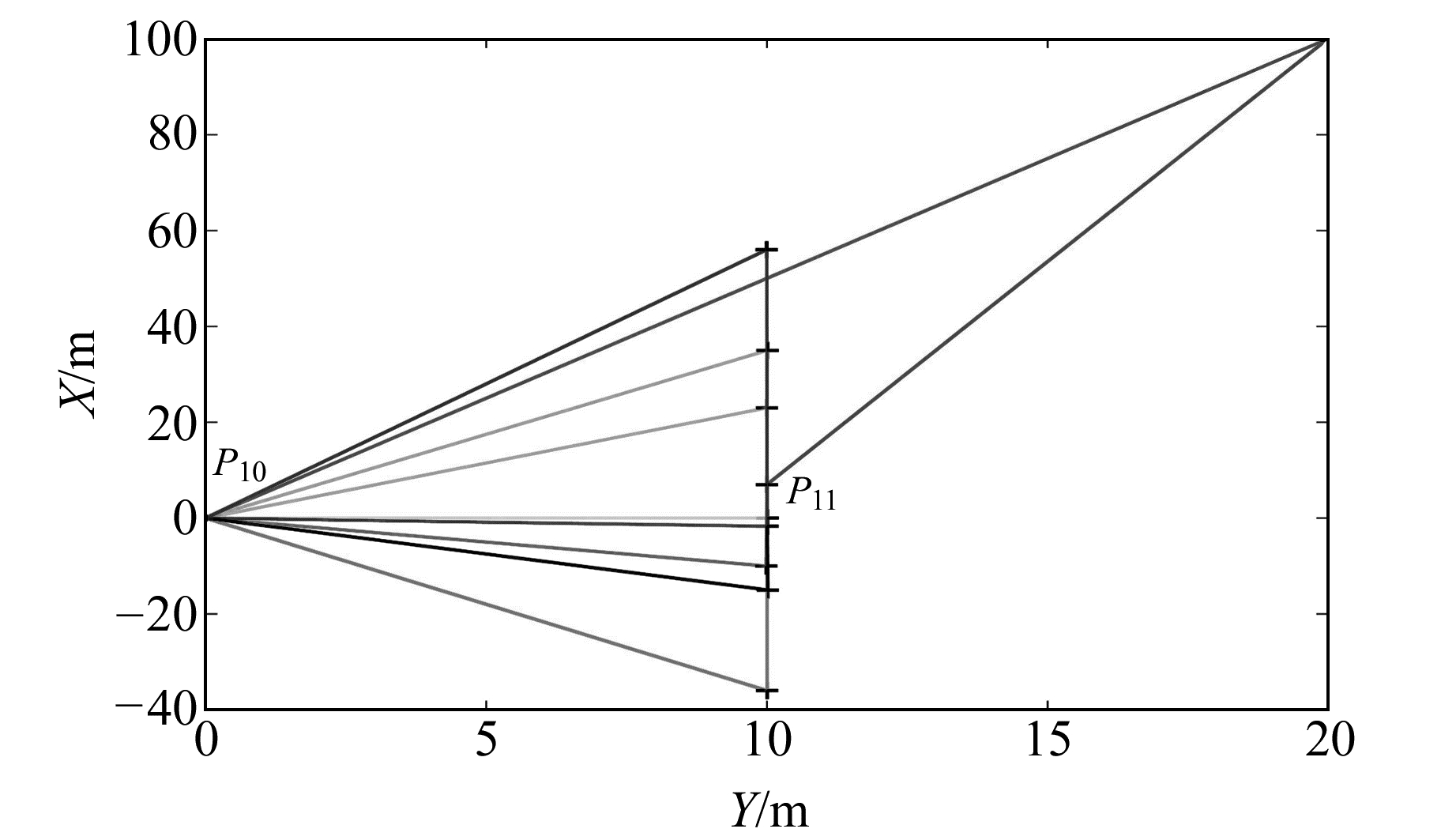
采用文献[11]中的病态测边网算例，该算例中有9个已知点(P₁, P₂, …, P₉)和2个未知点(P₁₀, P₁₁), 其点位平面分布见图 2。表 3为已知点坐标及其到未知点的距离观测值, P₁₀和P₁₁的真实坐标分别为(0, 0, 0)和(7, 10, -5), 其观测距离d_10，11=13.107 8 m, 各观测距离均为等精度观测, 可根据19个距离观测值组建误差方程，平差解算2个未知点坐标。

该算例中，法矩阵A^TA的条件数为4.585 1×10³，存在病态。同样的数值算例分别采用5种算法进行解算，其中等式约束条件为：

$ \begin{array}{*{20}{c}} {\left( {{{\hat X}_{10}}\quad {{\hat Y}_{10}}\quad {{\hat Z}_{10}}} \right) + \left( {{{\hat X}_{11}}\quad {{\hat Y}_{11}}\quad {{\hat Z}_{11}}} \right) = }\\ {(7\quad 10\quad - 5)} \end{array} $

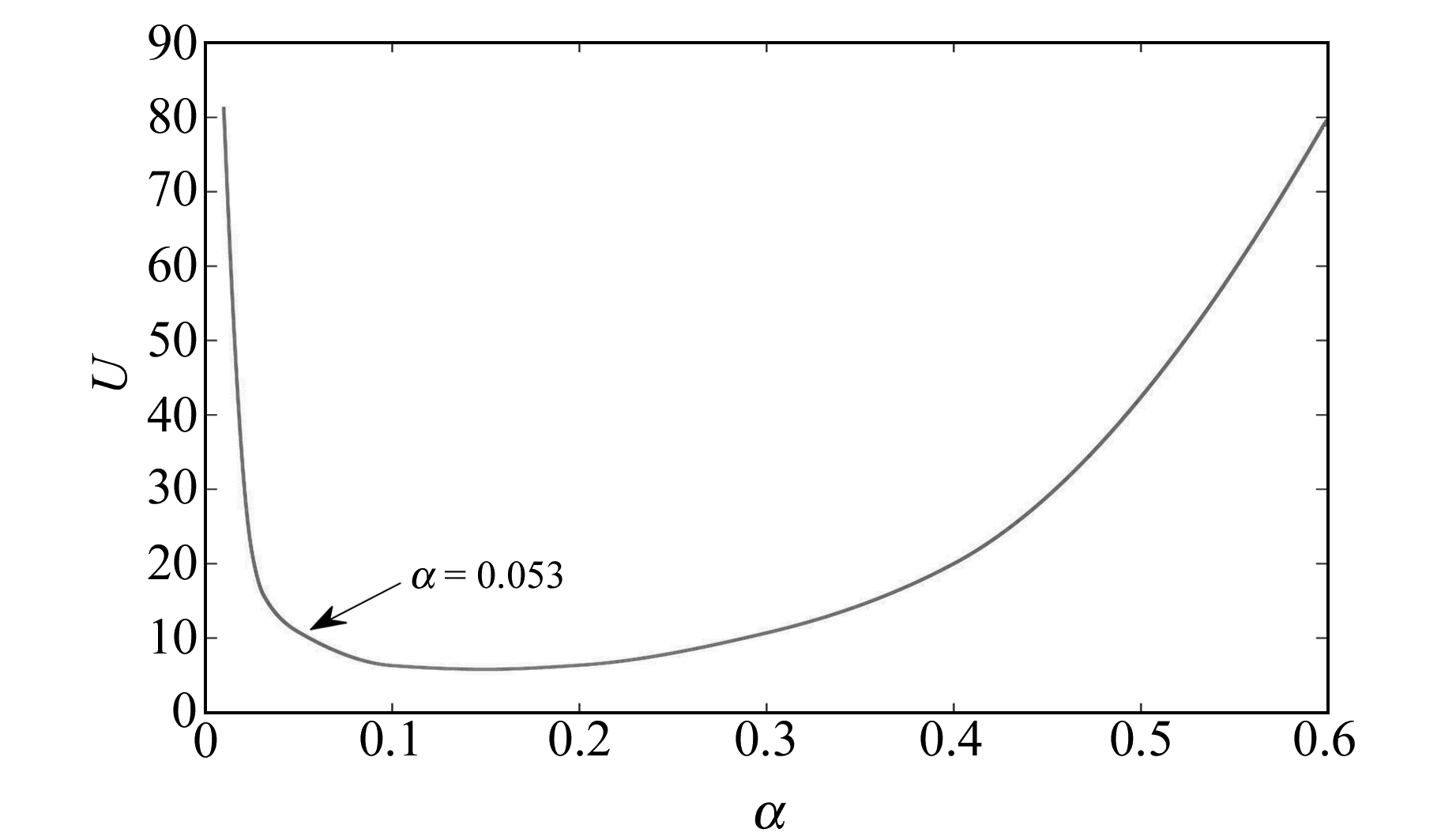
图 3为使用U曲线法确定正则化参数的示意图。比较不同算法获得的参数估值$\hat{\boldsymbol{X}}$与真值X的差值范数和相对偏差范数，结果见表 4，参数估值的单位权方差及方差-协方差阵估值见表 5。

3.3 算例分析

1) 由表 1和4可知，由于法矩阵病态性的影响，最小二乘解和总体最小二乘解严重偏离真值，数值算例中与真值的差值范数分别为1.308 8和6.719 0，病态测边网算例中与真值的差值范数分别为11.259 4和21.353 2。从结果来看，病态性对总体最小二乘解的影响远大于最小二乘，这也印证了孙同贺等^[10]的观点。

2) 袁振超法基于Tikhonov正则化原理，通过引入岭参数改善法矩阵的病态性，其解的精度较最小二乘解和总体最小二乘解有较大的提升, 与真值的差值范数分别为0.835 0和0.709 9；混合正则化法将Tikhonov正则化和TV正则化有效结合，克服了单一的Tikhonov正则化法造成解过度平滑的不足，精度相比袁振超法有所提升，与真值的差值范数分别为0.128 3和0.117 1。

3) 由表 1和4可知，加入正确的等式约束条件后，尽管法矩阵仍然病态，但约束总体最小二乘解的精度仍然有大幅度的提高；而本文提出的附加等式约束病态总体最小二乘正则化算法，既通过正则化改善了法矩阵的病态性，又顾及系数阵存在的误差，同时还考虑了正确的先验信息，其解的精度最高，与真值的差值范数分别为0.025 8和0.004 7。

4 结语

本文基于病态总体最小二乘模型，引入等式约束条件，建立了等式约束病态总体最小二乘模型，通过拉格朗日极值法导出约束病态总体最小二乘模型的正则化解迭代公式和精度评定公式。分别采用模拟的数值算例和病态测边网算例进行计算，比较最小二乘法(LS)、总体最小二乘法(TLS)、正则化算法(袁振超法)、混合正则化法、约束总体最小二乘法(CTLS)和约束总体最小二乘正则化算法(本文方法)的解，结果表明，本文方法解的精度最高。关于观测值和系数阵不等精度的情形和无偏单位权方差的估计，将是下一步的研究工作。