自20世纪80年代自主导航概念首次被提出后,多个卫星导航系统争相开始对这一技术展开研究[1-6]。目前,自主导航的数据处理模式主要分为集中式、分布式及分组式。其中,集中式是将所有的卫星观测数据都交给中心卫星统一处理,然后再将解算结果分发给各卫星[7]。相较于其他2种模式,集中式处理模式定轨精度高且不需要多颗卫星均具备数据处理功能。本文将采用集中式来进行自主导航。
由于星间链路数据的保密性以及我国北斗系统自主导航实验起步晚,大多数关于星间链路技术以及自主导航的研究都是基于仿真数据展开的[8]。为探讨不同特性的观测误差对北斗系统3类卫星自主导航精度影响的差异,本文采用参数分解滤波模型实现北斗系统的集中式自主导航。以北斗仿真星座为对象,采用自编软件对北斗系统的自主导航进行仿真验算,分别探讨观测噪声及残余系统误差对北斗系统3类卫星自主导航精度的影响,所得结论有益于北斗系统自主导航数据处理方法的研究及精度改进。
1 滤波模型及观测值仿真本文采用参数分解滤波模型来实现北斗系统的自主导航,在保证解算精度的情况下,其具有较高的解算效率[9]。
星间观测值仿真包括星间距离观测值的计算和观测误差的生成。星间距离观测值的仿真是按照一定的星间链路测距体制,利用精密星历信息结合星间链路拓扑构型原则计算出建链卫星间的几何距离,然后再加入信号发射卫星与信号接收卫星的钟差影响,最后加入相对论效应、观测噪声和残余系统误差而生成[9-10]。
2 仿真实验与分析利用自主研制开发的集中式实时自主导航软件,通过对北斗仿真星座进行60 d自主导航解算,验证分析观测噪声及残余系统误差对北斗系统3类卫星自主导航精度的影响。仿真过程及解算策略可参见文献[9-10]。
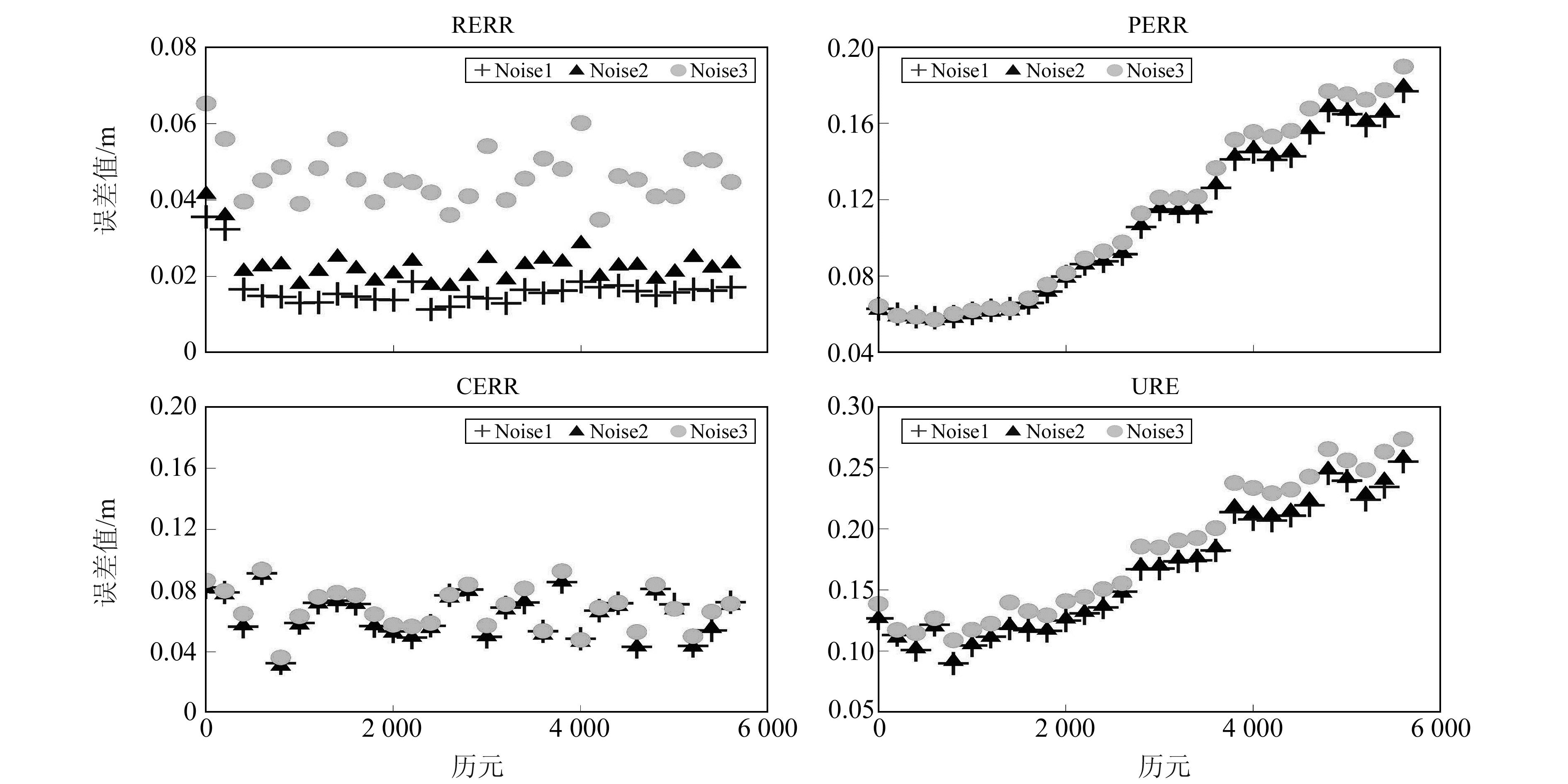
2.1 观测噪声对自主导航精度的影响分析分别采用观测噪声为10 cm、30 cm及75 cm的星间链路观测值对北斗仿真星座进行60 d集中式实时自主导航。仿真时未加入残余系统误差,星间链路波束角统一采用GEO:15°~75°,IGSO:15°~75°,MEO:30°~75°。图 1给出不同观测噪声方案下60 d自主导航全星座RMS历元偏差时序。图中RERR、PERR、CERR及URE分别表示径向误差、水平方向误差、相对钟差投影至距离的误差及用户距离误差,其中URE是前3种误差的综合反映,其具体解算公式可参照文献[1]。图中Noise1、Noise2及Noise3分别表示观测噪声为10 cm、30 cm及75 cm的解算结果。
|
图 1 不同观测噪声情况下60 d自主导航全星座RMS历元偏差时序 Fig. 1 Time series of RMS of 60 days' autonomous navigation calculation in different cases of observation noises |
由图可见,Noise1、Noise2及Noise3的RERR分别约为0.02 m、0.03 m及0.05 m,不随时间发散。由于自主导航缺少地面基准,星座整体旋转无法观测,故PERR将随时间延长逐渐增大。在自主导航第60天,Noise1、Noise2及Noise3的PERR分别约为1.51 m、1.52 m及1.55 m;对于CERR来说,其反映的是星座内部的相对钟差,故不随时间发散。3种方案下的CERR结果无明显差异,均约为0.08 m;对于URE而言,在自主导航第60天,3种观测噪声方案下结果分别约为0.22 m、0.22 m及0.23 m。通过以上分析可以看出,观测噪声对自主导航结果精度影响不大,仅为cm级。这是由于观测噪声的统计特性呈现白噪声,在滤波解算的过程中能够得到很好的改正。
为了比较GEO、IGSO及MEO卫星的结果差异,图 2给出在3种不同观测噪声情况下各卫星60 d历元平均URE统计结果。其中,PRN1~3为GEO卫星,PRN4~6为IGSO卫星,PRN7~30为MEO卫星。由图 2可见,对于大部分卫星而言,其60 d平均URE均随观测噪声的增大而增大,变化量级约为cm级。对于3类不同的卫星而言,观测噪声对结果的影响不存在显著差别。图中各卫星之间的结果差异是因为待估参数先验信息精度的不同,不会对本文结果分析产生影响。

|
图 2 不同观测噪声情况下各卫星60 d历元平均URE统计结果 Fig. 2 The epoch mean RMS for 60 days' autonomous navigation of each satellite in the different cases of observation noises |
分别采用5种不同残余系统误差方案下的仿真观测值对北斗仿真星座进行60 d集中式实时自主导航。仿真时观测噪声的均方差均取10 cm,星间链路的波束角仍采用§2.1中的方案,残余系统误差方案描述如表 1所示。
|
|
表 1 残余系统误差方案 Tab. 1 Schemes for residual system error |
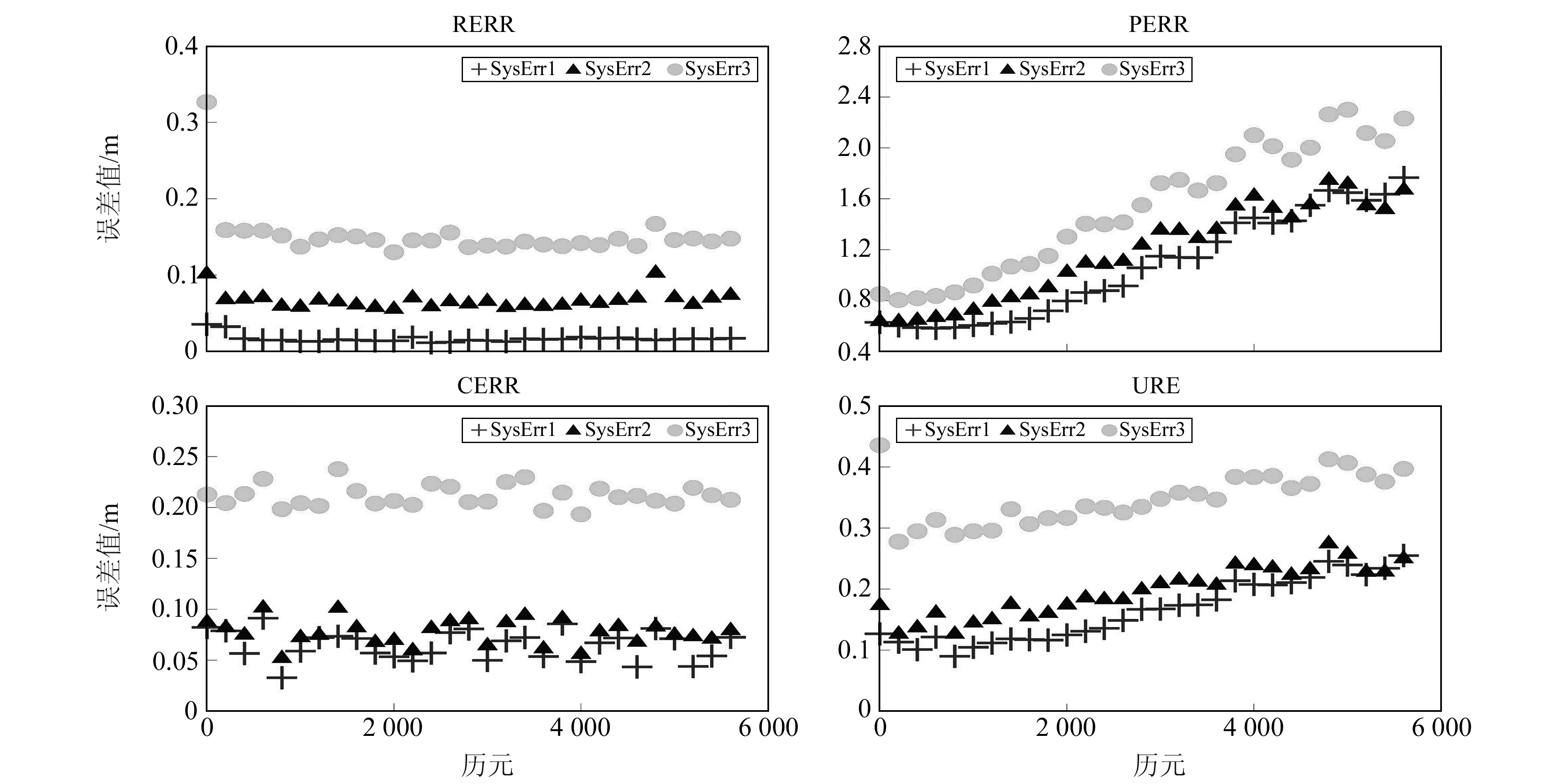
图 3给出SysErr1~3方案下60 d自主导航全星座RMS历元偏差时序。在这3种方案中,残余系统误差的固定项与周期项均同步增大。随着残余系统误差的增大,RERR、PERR、CERR及URE均逐渐增大。对于RERR,在SysErr1、SysErr2及SysErr3方案下,其结果分别约为0.02 m、0.07 m及0.14 m;CERR对应结果分别约为0.07 m、0.08 m及0.21 m;对于PERR,在3种方案下,其自主导航第60天结果分别约为1.51 m、1.65 m及2.24 m;URE对应结果分别约为0.23 m、0.25 m及0.40 m。从以上分析可以看出,残余系统误差对自主导航的影响显著,其影响量级约为dm级。观测值中若存在较大的残余系统误差,将严重影响自主导航精度。因此,在自主导航过程中,需要尽量改正观测值中的残余系统误差。
|
图 3 SysErr1~3方案下60 d自主导航全星座RMS历元偏差时序 Fig. 3 Time series of RMS of 60 days' autonomous navigation calculation in cases of SysErr1 to SysErr3 |
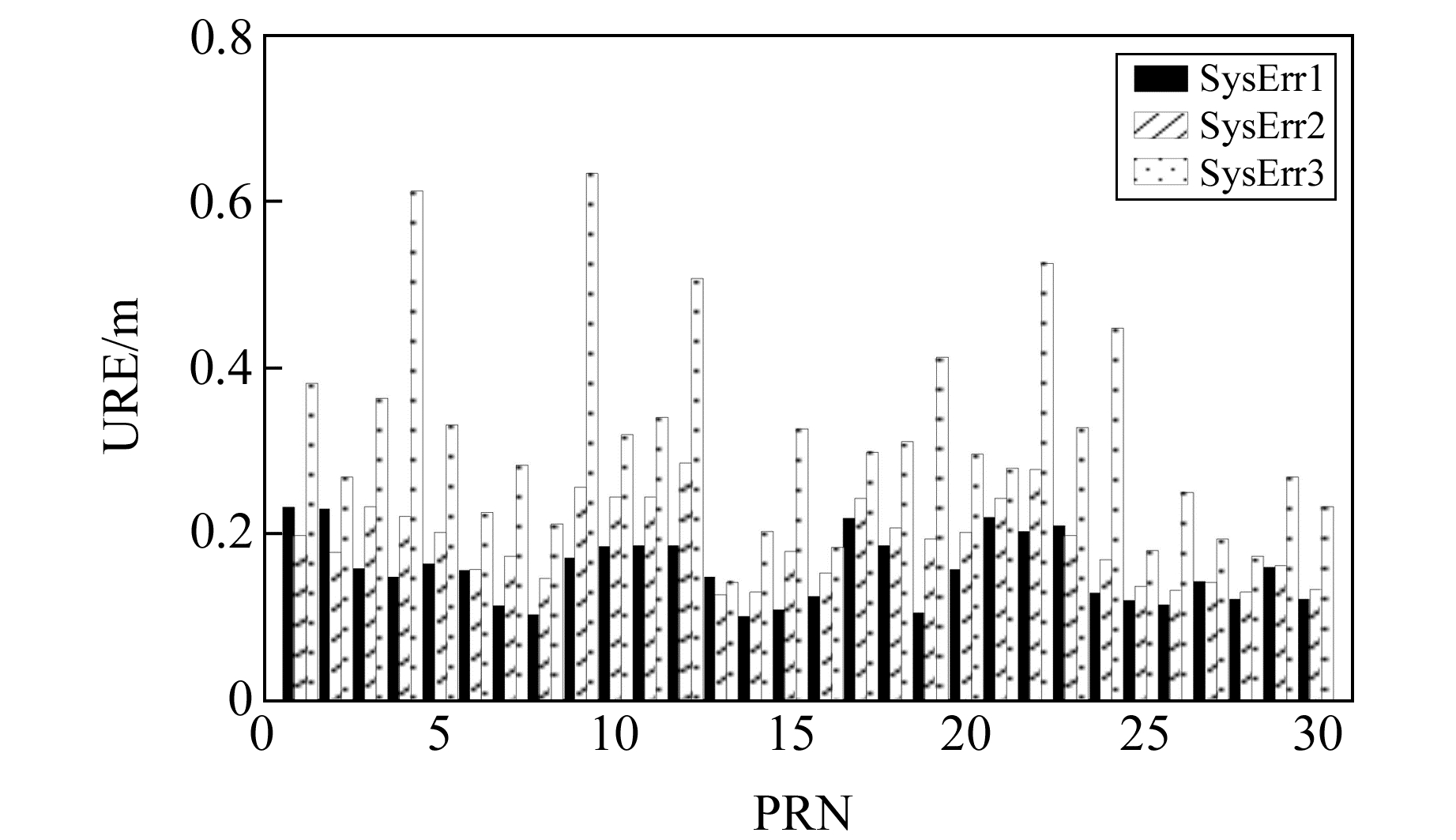
图 4给出SysErr1~3方案下各卫星60 d历元平均URE统计结果。由图可见,残余系统误差对3类卫星的自主导航结果均存在显著影响。当残余系统误差显著增大时(对应SysErr3方案的情况),各卫星的60 d平均URE亦显著增大。但对于3类不同的卫星而言,残余系统误差对其结果的影响同样不存在显著差别。
|
图 4 SysErr1~3方案下各卫星60 d历元平均URE统计结果 Fig. 4 The epoch mean RMS for 60 days' autonomous navigation of each satellite in cases of SysErr1 to SysErr3 |
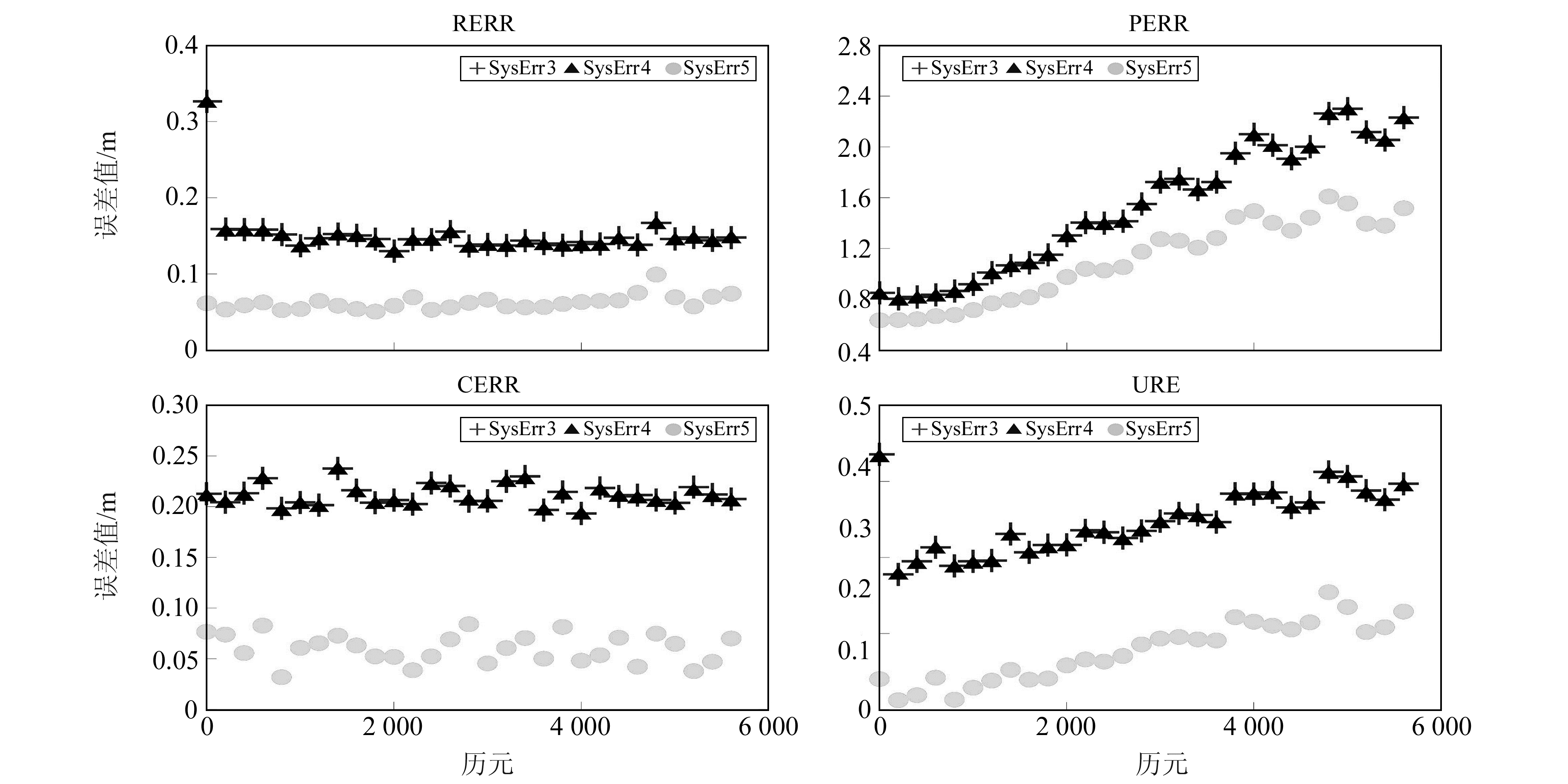
为了进一步探讨残余系统误差的固定项及周期项对自主导航解算结果的影响,图 5给出SysErr3~5方案下60 d自主导航全星座RMS历元偏差时序,其分别表示同时包含固定项及周期项系统误差、仅包含固定项系统误差、仅包含周期项系统误差的情况。由图可见,在定轨解算60 d中,SysErr3与SysErr4方案下的解算结果表现一致,这表明残余系统误差中的固定偏差为影响定轨精度的主要成分;而仅包含周期项系统误差的SysErr5与图 3中无系统误差的SysErr1解算结果表现一致,表明残余系统误差中的周期项能够在滤波解算中得到很好的改正。残余系统误差中的固定偏差主要来自信号收发设备的内部时延,在自主导航时需对此项进行认真检校。
|
图 5 SysErr3~5方案下60 d自主导航全星座RMS历元偏差时序 Fig. 5 Time series of RMS of 60 days' autonomous navigation calculation in cases of SysErr3 to SysErr5 |
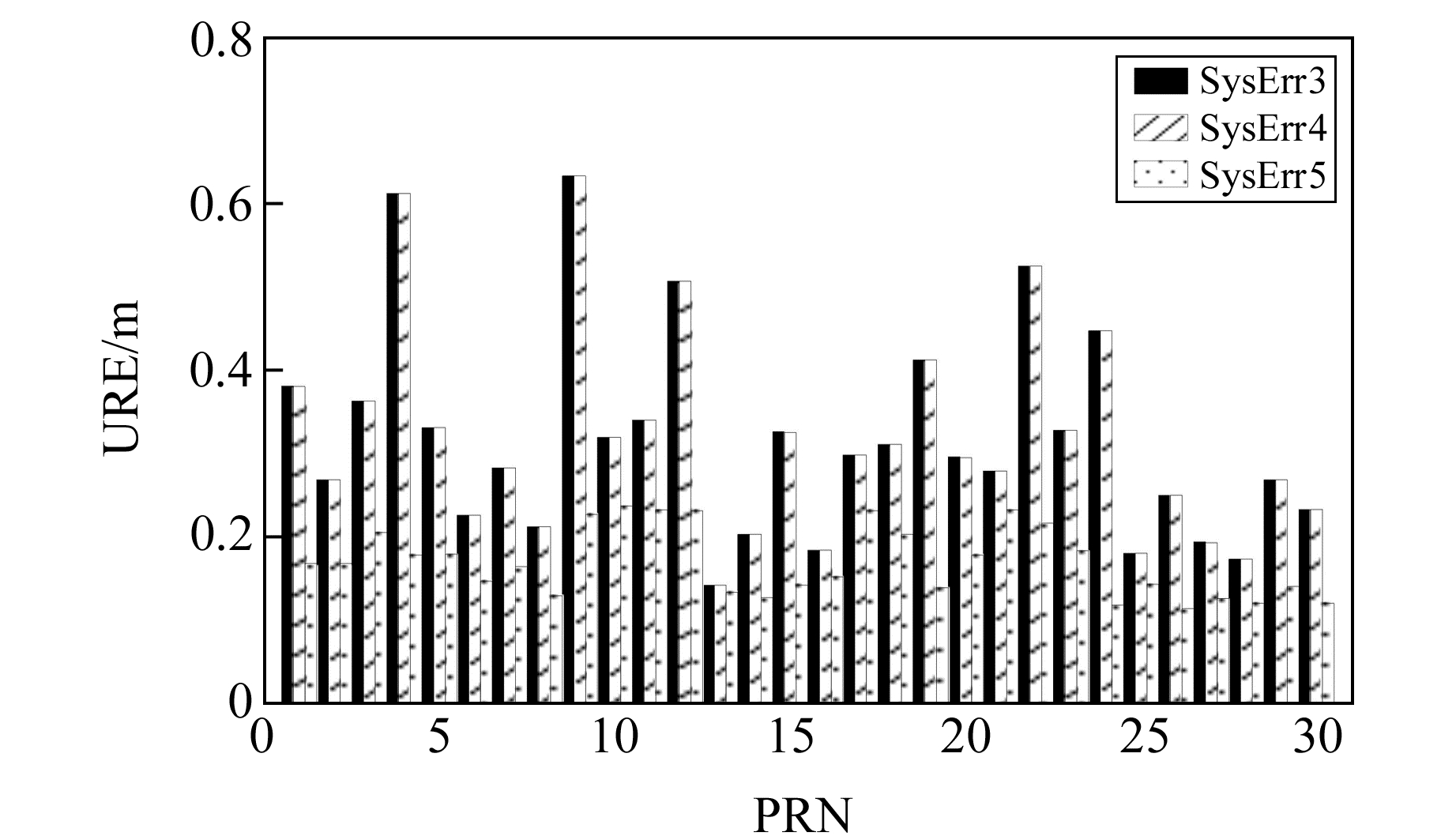
图 6给出SysErr3~5方案下各卫星60 d历元平均URE的统计结果。由图可见,SysErr3与SysErr4方案下3类卫星的解算结果一致,说明残余系统误差中的固定偏差为影响定轨精度的主要成分,这与图 5中的结论相互印证。
|
图 6 SysErr3~5方案下各卫星60 d历元平均URE统计结果 Fig. 6 The epoch mean RMS for 60 days'autonomous navigation of each satellite in cases of SysErr3 to SysErr5 |
本文采用集中式实时自主导航参数分解滤波算法,基于仿真数据进行60 d集中式实时自主导航解算,分析观测噪声及残余系统误差对北斗系统3类卫星自主导航精度的影响。在本文特定的仿真条件下,得到以下结论:
1) 观测噪声由于具有白噪声的特性,在滤波解算过程中能够得到很好的改正,其对自主导航解算没有显著影响。
2) 残余系统误差对自主导航的影响大小与其本身量级呈线性递增关系,当残余系统误差为dm级时,自主导航精度会明显降低。残余系统误差中的固定偏差为影响定轨精度的主要成分,因此在自主导航时,需要对残余系统误差中的固定偏差项(主要来源于观测信号收发设备的内部时延)进行认真检校。
3) 观测噪声及残余系统误差的变化对北斗系统3类卫星自主导航精度的影响无显著差异。
| [1] |
Ananda M P, Berstein H, Cunningham K E, et al. Global Positioning System Autonomous Navigation[J]. IEEE Position Location and Navigation Symposium, 2002, 27(1): 497-508
(  0) 0) |
| [2] |
李龙龙, 耿国桐, 李作虎. 国外卫星导航系统星间链路发展研究[J]. 测绘科学技术学报, 2016, 33(2): 133-138 (Li Longlong, Geng Guotong, Li Zuohu. Study of Development of the Inter-Satellite Links in Foreign GNSS[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 133-138)
(  0) 0) |
| [3] |
王冬霞. GNSS星间链路自主导航技术研究进展及展望[J]. 宇航学报, 2016, 37(11): 1279-1288 (Wang Dongxia. Development and Prospect of GNSS Autonomous Navigation Based on Inter-Satellite Link[J]. Journal of Astronautics, 2016, 37(11): 1279-1288 DOI:10.3873/j.issn.1000-1328.2016.11.001)
(  0) 0) |
| [4] |
宋小勇, 毛悦, 冯来平, 等. BD卫星星间链路定轨结果及分析[J]. 测绘学报, 2017, 46(5): 547-553 (Song Xiaoyong, Mao Yue, Feng Laiping, et al. The Preliminary Result and Analysis for BD Orbit Determination with Inter-Satellite Link Data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 547-553)
(  0) 0) |
| [5] |
郑坤, 董绪荣, 杨洋, 等. 一种基于GEO星间链路的导航系统时间同步新体制[J]. 武汉大学学报:信息科学版, 2014, 39(10): 1163-1167 (Zheng Kun, Dong Xurong, Yang Yang, et al. A New Time Synchronization System Based on the GEO ISLs[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1163-1167)
(  0) 0) |
| [6] |
陈金平, 胡小工, 唐成盼, 等. 北斗新一代试验卫星星钟及轨道精度初步分析[J]. 中国科学:物理学力学天文学, 2016, 46(11) (Chen Jinping, Hu Xiaogong, Tang Chengpan, et al. Orbit Determination and Time Synchronization for New-Generation Beidou Satellites: Preliminary Results[J]. Sci Sin Phys Mech Astron, 2016, 46(11) DOI:10.1360/SSPMA2016-00281)
(  0) 0) |
| [7] |
李征航, 龚晓颖, 刘万科. 误差与先验信息对导航卫星自主定轨的影响研究[J]. 武汉大学学报:信息科学版, 2011, 36(7): 44-48 (Li Zhenghang, Gong Xiaoying, Liu Wanke. Influence of Error and Prior Information to AOD of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 44-48)
(  0) 0) |
| [8] |
唐成盼, 胡小工, 周善石, 等. 利用星间双向测距数据进行北斗卫星集中式自主定轨的初步结果分析[J]. 中国科学:物理学力学天文学, 2017, 47(2) (Tang Chengpan, Hu Xiaogong, Zhou Shanshi, et al. Centralized Autonomous Orbit Determination of Beidou Navigation Satellites with Inter-Satellite Link Measurements: Preliminary Results[J]. Sci Sin Phys Mech Astron, 2017, 47(2))
(  0) 0) |
| [9] |
Gong X Y. Parameter Integration Filter and Parameter Decomposition Filter for Autonomous Navigation of BDS[J]. GPS Solutions, 2017, 21(3): 1405-1416 DOI:10.1007/s10291-017-0640-7
(  0) 0) |
| [10] |
龚晓颖, 徐韶光, 冯威. 星间链路构型对自主导航精度的影响分析[J]. 大地测量与地球动力学, 2017, 37(11): 1161-1165 (Gong Xiaoying, Xu Shaoguang, Feng Wei. Influence of Cross-Link Configuration to Auto-Navigation's Precision[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1161-1165)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

