大地震(M>7)的破裂尺度大,且持续时间长[1-2],会产生丰富的低频信号(如10 s以上周期)。低频及永久位移信号对于地震研究十分重要,是准确计算地震震级、滑动分布和地震矩张量反演等研究的基础[3-8]。然而,利用传统地震仪器(如强震仪)难以准确获取地震位移信号,尤其是低频位移信号。
目前力平衡式加速度计的频带响应范围一般为DC到50~200 Hz。理论上,加速度计的频带范围是从零频开始,但在实际观测中易受仪器噪声、背景噪声的影响而产生低频误差,因而无法获取准确的长周期地震动信息[9-11]。同时,近场强震动条件下,加速度计易受强烈地震波的影响产生倾斜或旋转,导致重力投影到仪器水平方向上,使恢复的速度或位移中产生显著的基线漂移现象[4, 7, 10, 12-14]。
削弱低频误差和基线漂移常用的方法是对加速度观测值进行高通滤波,但高通滤波方法会导致重要的低频地震信号及永久位移信号缺失,阻碍完整地震信号的准确获取,且在高通滤波截止频率的设置方面也没有统一的定论。Tolis等[15]将低频截止频率直接设置为固定值,如0.05 Hz,其缺点是舍弃了低于截止频率的有效信号;Bommer等[16]使用交互方法,即先设置0.1 Hz截止频率,然后逐步减小截止频率直至加速度积分速度和位移时间序列合乎物理实际(地震波离开后,速度趋于0,位移趋于常值),但该处理过程较为主观。
另一种方法是采用GNSS测量来削弱加速度计低频误差和基线漂移。GNSS测量能够获取绝对位置,利用高采样GNSS与加速度计进行数据融合,能够获取较为准确的低频乃至永久位移信号[7, 13, 17]。融合方法按照数据处理方法的不同可分为松组合和紧组合两类,松组合利用GNSS独立解算的位移同加速度数据融合,采用卡尔曼滤波和平滑算法获取宽频带位移;紧组合将加速度数据作为观测方程加入到GNSS精密单点定位解算中,通过实时或模拟实时的方法获取地震宽频带位移[7]。
振动台系统是振动传感器测试、检校和地震信号模拟的重要平台。国内外在振动台地震模拟方面进行了大量研究,研制了一系列不同尺寸、多自由度的振动台,主要应用于结构抗震的研究[18]。GNSS观测需要户外开阔的环境,户外振动台能够提供开阔的观测条件,而在地震监测研究中,采用大型振动台实验成本高、周期长,操作难度大,因而利用小型振动台系统进行相关研究是一种简便、可行的方式。
综上所述,针对加速度计低频测量特性和高通滤波截止频率难以确定的问题,本文利用小型振动台系统,通过一系列振动实验,从时域(加速度获取位移)和频域(信号功率谱分析)2个方面对加速度计低频测量特性进行研究。在此基础上, 针对加速度计低频测量能力不足的缺陷,并置GNSS与加速度计,并使用加速度计和GNSS数据融合方法,以期在时域和频域上准确恢复低频位移信号。
1 方法 1.1 时间系统的统一时间系统和时标的统一是数据融合处理与分析的基础。GPS测量的时间系统为GPS时(GPST);加速度计采用GPS天线授时;强震加速度计直接采用北京时;振动台实验系统由计算机控制,计算机时间采用北京时。本文将加速度计测量值时、GNSS测量值时、振动台测量值时统一为GPS时。
1.2 加速度功率谱分析及积分方法利用Welch功率谱分析方法对加速度计原始数据进行功率谱分析,求取各频率信号下的功率谱密度(power spectral density,PSD)。如式(1)所示,定义表征加速度计原始加速度数据的功率谱密度与振动台加速度参考值的功率谱密度比值关系Ratio(记作R)为衡量加速度计原始数据信号频率准确度的量化指标:
| $R=10 \log \left(\frac{P_{\mathrm{acc}}}{P_{\mathrm{ref}}}\right) $ | (1) |
式中,Pacc为加速度计在该振动信号频率下的功率谱密度,Pref为振动台参考加速度在同振动信号频率下的功率谱密度,单位均为(m/s2)2/Hz。
加速度数据处理步骤为:1)去除振动前20 s零偏并进行高通滤波;2)对加速度数据积分得到速度;3)扣除振动前20 s速度均值,进行高通滤波后积分得到位移时间序列。其中,高通滤波利用3阶巴特沃斯高通滤波器,并使用零相位滤波方法,采用高低不同的截止频率对不同频率振动信号进行处理。
1.3 GNSS与加速度计数据融合方法采用短基线双差方法处理GNSS数据,GNSS流动站的坐标解算精度为平面2~4 mm,高程3~8 mm。
采用卡尔曼滤波及平滑方法对GNSS与加速度计数据进行融合[14],即利用GNSS独立解算的坐标时间序列和加速度计原始测量数据建立卡尔曼滤波状态方程和观测方程,采用正向滤波及反向平滑方法解算得到GNSS与加速度计融合的位移和速度时间序列结果。
2 实验数据及处理为了研究加速度计在低频振动条件下的测量特性,进行一系列低频振动实验。实验采用Quanser公司ShakeTable Ⅱ单轴振动台系统、珠海泰德TDA-33M力平衡式加速度计以及Trimble NetR9 GNSS接收机和天线。仪器设备的主要参数如表 1所示。
|
|
表 1 低频振动实验仪器设备主要参数 Tab. 1 Main parameters of experiment instruments |
加速度计是高精度、高灵敏度传感器,使用时需要保证仪器安装平稳,并尽可能减少外界环境噪声的干扰。因此,设计重达260 kg的移动式钢板基座和可水平调节的台面,将振动台固定在水平台面上。之后,将加速度计和GNSS流动站天线固定安装在振动台面上。通过定向测量,将振动台坐标系与地理坐标系对齐。GNSS基准站架设在振动台附近5 m。
2018-02-01在武汉大学信息学部操场进行实验,加速度计采样率设置为100 Hz,GNSS数据采样率设置为5 Hz,振动台正弦波振动信号振幅设置为5 cm,频率和振动时长如表 2所示。
|
|
表 2 振动实验正弦信号频率 Tab. 2 Sinusoidal signal frequencies of vibration experiment |
振动台上具有高精度的电机和编码器,位移精度为μm级。振动台记录数据包括振动位移、速度和加速度,其中,速度和加速度通过振动台由位移微分处理得到的。利用上文方法对数据进行处理和分析。
3 结果与分析为了在时域和频域上充分展示加速度计低频信号测量特性,利用上述方法对实验数据进行处理,包括加速度功率谱分析、加速度积分位移分析以及GNSS与加速度计数据融合。
3.1 噪声评估对加速度计进行静置测试和低频振动测试,包括:1)静置加速度计测试,时长1 000 s;2)极低频振动测试(振幅5 cm,周期1 000 s的正弦信号)。静置加速度计测试直接评估环境背景噪声的大小;极低频测试与静置测试形成对照,评估低频振动条件下的环境噪声。
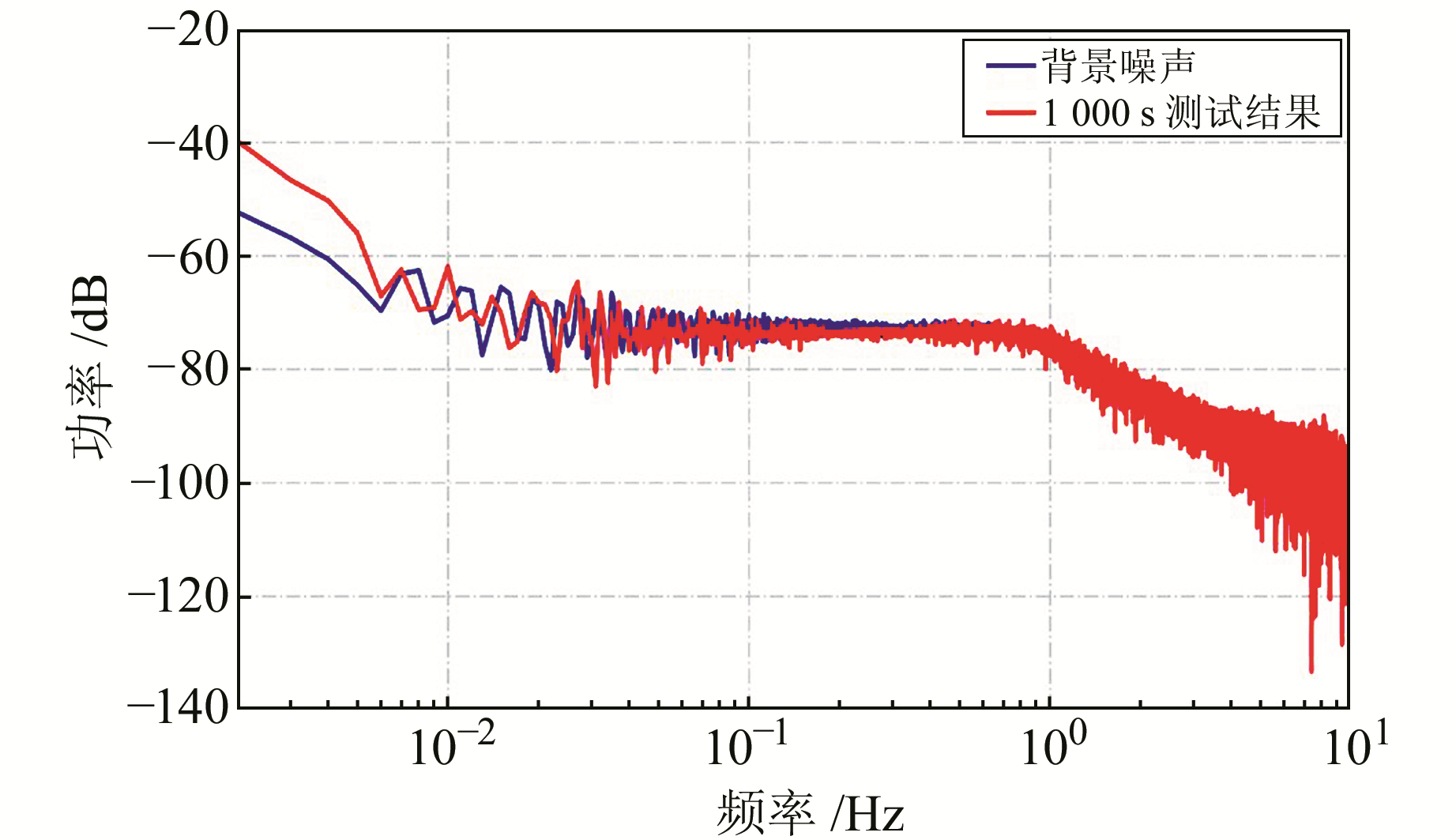
本文主要研究频率在1 Hz以下的低频信号,对2组数据进行截止频率为1 Hz的低通滤波,并进行功率谱分析,结果如图 1所示。
|
图 1 加速度计静止噪声与低频振动噪声对比 Fig. 1 Accelerometer power spectrum of static test and slow-shaking test |
由静置时的功率谱密度(蓝线)可以看出,在0.005 Hz以上,信号功率在-60 dB以下,低频环境噪声并不显著;与1 000 s低频振动测试结果对比可以发现,在0.007 Hz以上时,二者差异不显著。因此,在本文研究频段内,背景噪声影响十分微弱。
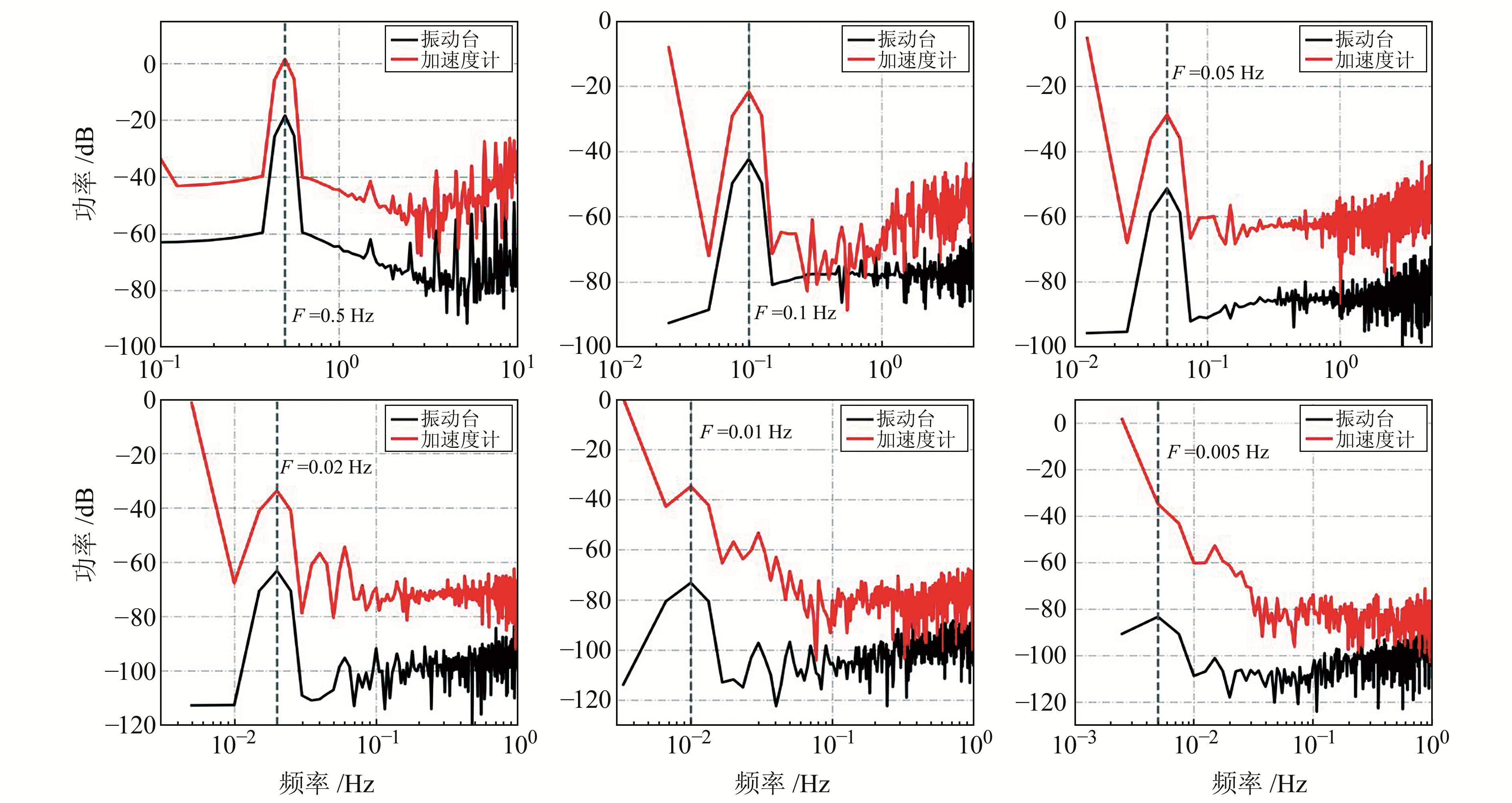
3.2 功率谱分析利用表 2中的信号频率进行振动测试,选取整数周期时长的数据,功率谱结果如图 2所示。对加速度计功率谱密度(红线)和振动台参考加速度值的功率谱密度(黑线)进行对比,展示0.005~0.5 Hz间部分频率振动信号下二者的加速度功率谱密度。可以看出,振动台PSD与加速度计PSD之间存在系统性偏差,且这种系统性偏差是普遍存在的,这是由于振动台系统与加速度计传感器差异造成的。加速度计原始测量值包含多种测量噪声,如振动台机械结构噪声;而振动台加速度是由振动台位移微分得到的,其位移是由高精度位移编码器记录的,振动台采样率高达2 000 Hz,高精度编码器位移精度为μm级,微分误差可以忽略不计。由图 2可以看出,随着振动信号频率的减小,振动台加速度参考值PSD与加速度测量值PSD之间的差异越来越大,表明随着被测信号频率的降低,加速度计信噪比降低。
|
图 2 不同振动频率加速度信号功率谱分析 Fig. 2 Acceleration PSD of different vibration frequencies |
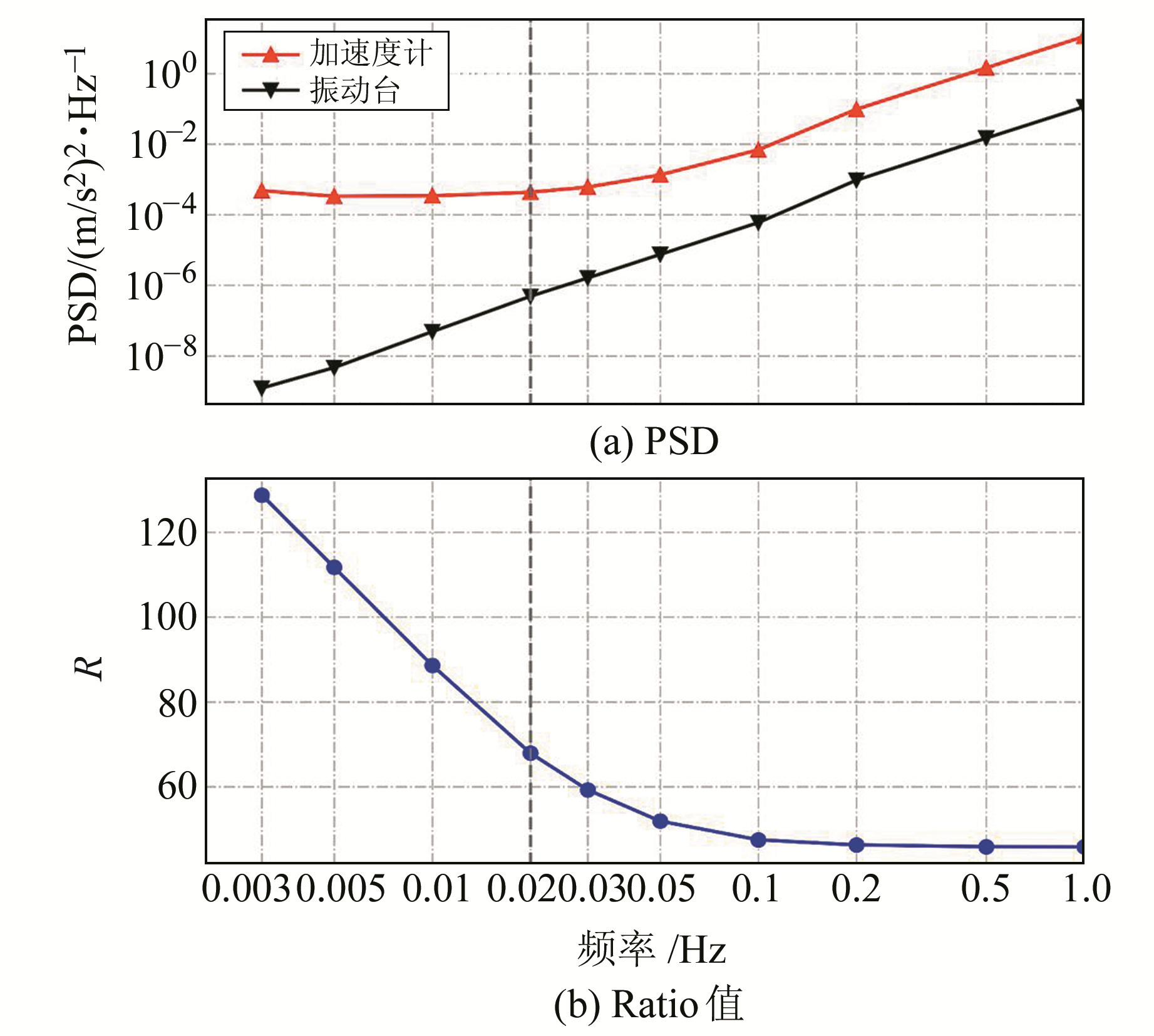
为了更好地表征加速度计噪声随频率的变化关系,利用式(2)所述方法计算不同振动信号频率下的加速度计测量值和振动台参考值PSD及对应的Ratio值。如图 3所示,红色线和黑色线分别表示加速度计观测值及振动台加速度参考值PSD随频率的分布,蓝色线表示Ratio值随频率的分布。可以看出,振动台参考值的PSD与频率近似呈比例关系,这也符合信号功率谱的规律。在频率大于0.02 Hz时,加速度计的PSD与频率也近似呈比例关系,且此时Ratio值较小;反之,在频率小于0.02 Hz时,随着振动信号频率的减小,加速度计观测值的PSD不再如参考值规律减小,且Ratio值随着频率的减小而显著增大。从功率谱分析可以看出,信号频率越低,加速度计低频误差越显著,测量值可靠性随之下降。
|
图 3 加速度计和振动台参考值PSD及Ratio值对比 Fig. 3 PSD/Ratio comparison between accelerometer and reference values |
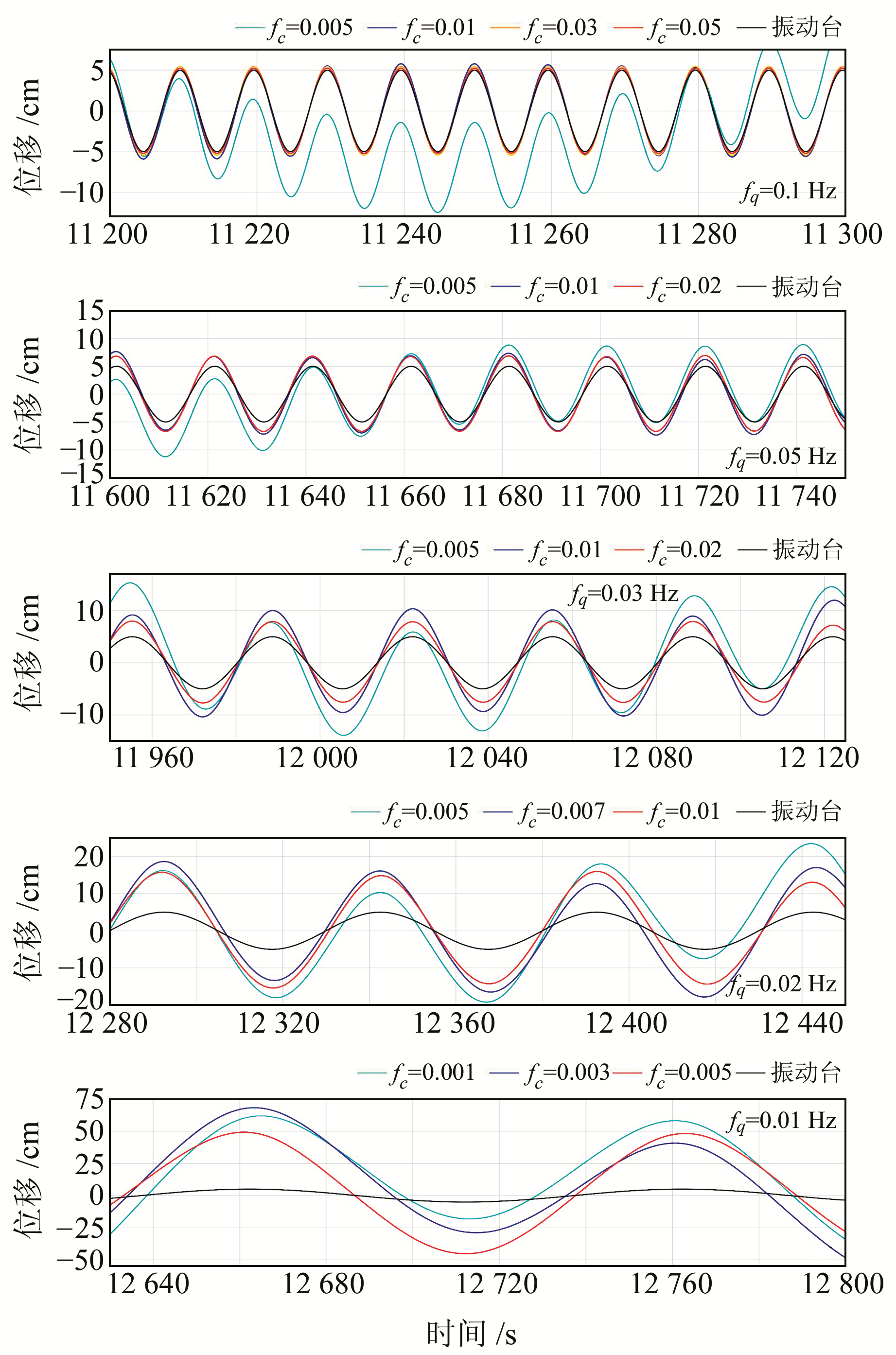
对加速度数据进行积分,位移时间序列结果如图 4所示,从上至下表示不同频率振动信号(0.1~0.01 Hz),fq表示振动信号频率,fc表示高通滤波截止频率。整体来看,位移信号序列的频率准确,且随着振动信号频率的降低,位移积分误差呈增大趋势。0.1 Hz振动信号的积分位移精度较高,fc为0.01 Hz时就能恢复出较为精确的位移,增加fc对信号幅度影响不显著;信号频率在0.05 Hz,fc为0.01 Hz时,位移幅值误差在1.6 cm左右;信号频率在0.03 Hz,fc为0.01 Hz时,位移幅值误差在5 cm左右;信号频率在0.02 Hz,fc为0.007 Hz时,位移幅值误差在10 cm左右;小于0.02 Hz信号时,加速度计积分位移与参考位移偏差显著,表明加速度误差随着振动信号频率的降低变得显著,这也与功率谱分析的结果一致。从积分位移上来说,加速度计容易受到多种误差的影响,无法准确获取低频信号位移,尤其当信号在0.05 Hz以下时,随着信号频率的降低,恢复的位移误差将显著增大。
|
图 4 不同频率信号下加速度计积分位移、振动台参考位移对比 Fig. 4 Displacement comparison between acceleration integration and reference values |
通过上述分析可知,加速度计在测量时会受到低频误差的影响,导致无法准确恢复振动位移信号。在此引入GNSS测量,利用上文方法,对GNSS与加速度计进行数据融合,位移结果如图 5所示。

|
图 5 GNSS位移、加速度计积分位移、GNSS与加速度计融合位移、振动台参考位移功率谱密度对比 Fig. 5 Displacement comparison among GNSS, GNSS accelerometer data fusion and reference values |
图 5(a)、(b)分别是振动信号频率为0.01 Hz及0.005 Hz时对应的GNSS位移、振动台真实位移及GNSS与加速度计融合位移对比图。可以看出,利用GNSS与加速度计融合后,在振动信号频率为0.005 Hz时仍然能够获得2 mm左右的位移精度,且平滑结果略优于仅滤波的结果。
为进一步研究GNSS与加速度计融合位移的频率特性,对上述振动台参考位移(shake table truth)、加速度计积分位移(acc)、GNSS位移(GPS)、GNSS与加速度计数据融合位移(GPS+acc)进行功率谱分析,功率谱密度结果如图 6所示。其中,在振动信号上,加速度计积分位移PSD值比振动台参考值大,表明加速度计积分成位移的结果中包含较多低频误差;GNSS位移在低频段较为准确,高频段噪声较大,融合位移在高频部分优于GNSS位移,在低频部分基本一致,且与参考位移一致。结果表明,利用高采样GNSS与加速度计融合方法能够有效弥补加速度计低频测量能力不足的缺点,使低频位移更加准确可靠。

|
图 6 GNSS、GNSS加速度计数据融合、振动台参考值位移对比 Fig. 6 Displacement PSD comparison among GNSS, acceleration integration, data fusion and reference values |
本文搭建的振动台系统能够为加速度计测试提供一种简易、可行的方法,可作为地震相关研究的基础平台。采用该系统对加速度计进行测试,结果表明,当信号频率高于0.05 Hz时,对加速度计信号进行高通滤波后积分能够恢复出较为准确的振动位移;随着振动信号频率的降低,加速度计恢复出的位移信号误差显著增大。该结论从功率谱分析中也得到验证,即Ratio值随着频率降低而显著变大,表明加速度计低频信号测量可靠性下降。研究结果为用户合理选择加速度计可用频带提供了一定的参考。
此外,GNSS与加速度计进行数据融合,能有效弥补加速度计低频测量可靠性不足的缺点,成功地恢复了低至0.005 Hz(周期为200 s)的振动信号位移,标准差在2 mm左右。时域及频域分析结果表明,利用GNSS与加速度计融合是解决加速度计低频测量能力不足、准确获取宽频带乃至永久位移的有效方法。
| [1] |
Wells D L, Coppersmith K J. New Empirical Relationships Among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement[J]. Bulletin of the Seismological Society of America, 1994, 84(4): 974-1 DOI:10.1007/BF00808290
(  0) 0) |
| [2] |
孙银涛, 徐国栋, 龙海云, 等. 震级与破裂长度统计关系研究[J]. 地震学报, 2016, 38(5): 803-806 (Sun Yintao, Xu Guodong, Long Haiyun, et al. Relationship between Magnitude and Rupture Length[J]. Acta Seismologica Sinica, 2016, 38(5): 803-806)
(  0) 0) |
| [3] |
Allen R M, Ziv A. Application of Real-Time GPS to Earthquake Early Warning[J]. Geophysical Research Letters, 2011, 38(16)
(  0) 0) |
| [4] |
Wang R J, Schurr B, Milkereit C, et al. An Improved Automatic Scheme for Empirical Baseline Correction of Digital Strong-Motion Records[J]. Bulletin of the Seismological Society of America, 2011, 101(5): 2029-2044 DOI:10.1785/0120110039
(  0) 0) |
| [5] |
Wang R J, Parolai S, Ge M, et al. The 2011 MW9.0 Tohoku Earthquake: Comparison of GPS and Strong-Motion Data[J]. Bulletin of the Seismological Society of America, 2013, 103(2B): 1336-1347 DOI:10.1785/0120110264
(  0) 0) |
| [6] |
Melgar D, Crowell B W, Geng J, et al. Earthquake Magnitude Calculation without Saturation from the Scaling of Peak Ground Displacement[J]. Geophysical Research Letters, 2015, 42(13): 5197-5205 DOI:10.1002/2015GL064278
(  0) 0) |
| [7] |
Geng J, Bock Y, Melgar D, et al. A New Seismogeodetic Approach Applied to GPS and Accelerometer Observations of the 2012 Brawley Seismic Swarm: Implications for Earthquake Early Warning[J]. Geochemistry Geophysics Geosystems, 2013, 14(7): 2124-2142 DOI:10.1002/ggge.20144
(  0) 0) |
| [8] |
Fang R X, Shi C, Song W W, et al. Determination of Earthquake Magnitude Using GPS Displacement Waveforms from Real-Time Precise Point Positioning[J]. Geophysical Journal International, 2014, 196(1): 461-472 DOI:10.1093/gji/ggt378
(  0) 0) |
| [9] |
Chiu H C. Stable Baseline Correction of Digital Strong-motion Data[J]. Bulletin of the Seismological Society of America, 1997, 87(4): 932-844
(  0) 0) |
| [10] |
于海英, 江汶乡, 解全才, 等. 近场数字强震仪记录误差分析与零线校正方法[J]. 地震工程与工程振动, 2009, 29(6): 1-12 (Yu Haiying, Jiang Wenxiang, Xie Quancai, et al. Baseline Correction of Digital Strong-Motion Records in Near-Field[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 1-12)
(  0) 0) |
| [11] |
周雍年. 强震动观测技术[M]. 北京: 地震出版社, 2011 (Zhou Yongnian. Strong Motion Observation Technique[M]. Beijing: Seismological Press, 2011)
(  0) 0) |
| [12] |
Boore D M. Effect of Baseline Corrections on Displacements and Response Spectra for Several Recordings of the 1999 Chi-Chi, Taiwan, Earthquake[J]. Bulletin of the Seismological Society of America, 2001, 91(5): 1199-1211
(  0) 0) |
| [13] |
Bock Y, Melgar D, Crowell B W. Real-Time Strong-Motion Broadband Displacements from Collocated GPS and Accelerometers[J]. Bulletin of the Seismological Society of America, 2011, 101(6): 2904-2925 DOI:10.1785/0120110007
(  0) 0) |
| [14] |
Melgar D, Bock Y, Sanchez D, et al. On Robust and Reliable Automated Baseline Corrections for Strong Motion Seismology[J]. Journal of Geophysical Research: Solid Earth, 2013, 118(3): 1177-1187 DOI:10.1002/jgrb.50135
(  0) 0) |
| [15] |
Tolis S V, Faccioli E. Displacement Design Spectra[J]. Journal of Earthquake Engineering, 1999, 3(1): 107-125
(  0) 0) |
| [16] |
Bommer J J, Elnashai A S. Displacement Spectra for Seismic Design[J]. Journal of Earthquake Engineering, 1999, 3(1): 1-32
(  0) 0) |
| [17] |
Saunders J K, Goldberg D E, Haase J S, et al. Seismogeodesy Using GPS and Low-Cost MEMS Accelerometers: Perspectives for Earthquake Early Warning and Rapid Response[J]. Bulletin of the Seismological Society of America, 2016, 106(6): 2469-2489 DOI:10.1785/0120160062
(  0) 0) |
| [18] |
王燕华, 程文瀼, 陆飞, 等. 地震模拟振动台的发展[J]. 工程抗震与加固改造, 2007, 29(5): 53-56 (Wang Yanhua, Cheng Wenrang, Lu Fei, et al. Development of the Shaking Table[J]. Earthquake Resistant Engineering and Retrofitting, 2007, 29(5): 53-56 DOI:10.3969/j.issn.1002-8412.2007.05.011)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

