利用GNSS建立电离层模型已比较成熟,但针对其参数估计随机模型的探讨并不多,即如何更合理设计观测权还有待深入研究。在实际数据处理中,权的确定方法主要有2种:经验定权方法(又称主观定权方法)和客观定权方法[1]。GNSS卫星的硬件延迟(differential code bias, DCB)通常采用主观定权方法,即等精度定权和高度角定权。等精度定权认为各卫星观测间噪声水平相同,且不随时间变化,这显然与实际不符[2]。事实上,卫星观测精度与接收机类型、卫星高度角、观测环境等息息相关。高度角定权是根据卫星的高度角来确定观测量的先验方差,其在参数估计和稳定性方面优于等精度定权。高度角定权虽然能在一定程度上降低高度角较大对观测误差的影响,但在选取截止高度角时,存在较大的主观性和不确定性[3]。
等精度定权和高度角定权等经验定权法虽然简单易行,但主观性强,往往忽略了观测值其他随机因素对参数估计的影响[4]。本文基于实时去噪和码、相位观测数据的实时加权联合处理的思想,提出一种更客观的观测权分配方法,即变异系数赋权法,顾及观测值多种随机影响因素,提高GPS-DCB解算精度及稳定性。
1 GNSS硬件延迟计算模型双频组合观测值不但能消除电离层延迟对不同频率观测值的影响,还能测定电离层天顶方向总电子含量值VTEC(vertical total electron content)[5]。
| $ \begin{array}{*{20}{c}} {\rho = P - \frac{{0.4028}}{{{f^2}}} \times F\left( z \right) \times }\\ {{\rm{VTEC}} + c\left( {{\rm{d}}s - {\rm{d}}r} \right) + \varepsilon } \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {\rho = \lambda \left( {N + \phi } \right) + \frac{{0.4028}}{{{f^2}}} \times F\left( z \right) \times }\\ {{\rm{VTEC}} + c\left( {{\rm{d}}s - {\rm{d}}r} \right) + \varepsilon } \end{array} $ | (2) |
式(1)和式(2)为仅考虑频率引起的弥散误差时的伪距和载波相位观测值表达式,P为伪距观测值,f为GPS工作频率,(ds-dr)为GNSS系统的硬件延迟,其中ds和dr分别为卫星硬件延迟和接收机硬件延迟,λ为波长,ϕ和N分别为整周模糊度和相位观测量,c为光速,ε为改正项,包括接收机、卫星钟差、对流层延迟改正等,F(z)为电离层投影函数,z为卫星天顶距。利用式(1)和式(2)得VTEC计算公式:
| $ {\rm{VTEC}} = k\left( {{P_2} - {P_1}} \right) + ck\left( {{\rm{d}}s - {\rm{d}}r} \right) $ | (3) |
| $ {\rm{VTEC}} = k\left( {{L_1} - {L_2}} \right) + ck\left( {{\rm{d}}s - {\rm{d}}r} \right) $ | (4) |
式中,$k=\frac{f_{1}^{2} f_{2}^{2}}{0.402\; 8\left(f_{1}^{2}-f_{2}^{2}\right)}$。由于载波相位本身存在模糊度参数,不适合构建模型,因此常用伪距观测值建立求解模型。为提高伪距观测值的精度,利用GNSS相位平滑伪距代替原始伪距观测值[6],则式(3)变为:
| $ {\rm{VTEC}} = k\left( {{{\bar P}_2} - {{\bar P}_1}} \right) + ck({\rm{d}}s - {\rm{d}}r) $ | (5) |
式中,Pi=1, 2为平滑后的伪距观测值。
本文基于4阶球谐函数模型,联合相位平滑伪距观测模型构建电离层模型[7]。4阶球谐函数模型为:
| $ \begin{array}{*{20}{c}} {{\rm{VTEC}} = \sum\limits_{i = 0}^4 {\sum\limits_{m = 0}^i {\left( {A_n^m\cos m{\lambda ^\prime } + } \right.} } }\\ {\left. {B_n^m\sin m{\lambda ^\prime }} \right) \times P_n^m\sin \varphi } \end{array} $ | (6) |
式中,Pnmcosφ为正则化的缔合勒让德函数[8],φ为穿刺点的地理纬度,λ′为穿刺点经线与过地心-太阳连线的经线之间的夹角,Anm、Bnm为未知的球谐函数系数。由式(5)和式(6)得:
| $ \begin{array}{*{20}{c}} {k\left( {{{\bar P}_2} - {{\bar P}_1}} \right) + ck({\rm{d}}s - {\rm{d}}r) = }\\ {\sum\limits_{i = 0}^4 {\sum\limits_{m = 0}^i {\left( {A_n^m\cos m{\lambda ^\prime } + B_n^m\sin m{\lambda ^\prime }} \right)} } \times P_n^m\sin \varphi } \end{array} $ | (7) |
对式(7)各项展开,构建误差方程:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat x}} - \mathit{\boldsymbol{l}} $ | (8) |
式中,B为系数矩阵,$\hat{\boldsymbol{x}}$为待求参数,l为相位平滑差分值。随机模型为:
| $ \mathit{\boldsymbol{P}} = \sigma _0^2{\mathit{\boldsymbol{D}}_0} = {\mathit{\boldsymbol{Q}}^{ - 1}} $ | (9) |
式中,σ02为单位权方差,D0、Q分别为观测值的方差阵和协因数阵。由于解算中将测站和卫星的硬件延迟分别设置为独立的参数进行平差解算,构建法方程系数矩阵秩亏,需引入一个约束条件。目前普遍采用的约束条件为:
| $ \sum\limits_{i = 1}^n {{d_i}} = 0 $ | (10) |
式中,n为观测到的卫星个数,di为第i颗卫星的硬件延迟。
权阵P可考虑采用以下2种经验权函数:
1) 等精度定权。当某一历元观测的卫星个数为n时,可以组成(n-1)个双差观测值。若不考虑观测值卫星间及历元间的任何相关性,并认为原始观测值的精度相同,即近似认为各系统观测值为等权观测值,将权矩阵看成是单位阵[9]。
2) 高度角定权。高度角随机模型是利用观测值的高度角为变量构成高度角的函数,即
| $ \sigma = f\left( {{\rm{elv}}} \right) $ | (11) |
式中, elv为卫星高度角。这类高度角函数主要有指数函数模型、正弦函数模型及正切函数模型等,其中最常用的为正弦函数模型[10-11],即
| $ {\sigma ^2} = 1/{\sin ^2}\left( {{\rm{elv}}} \right) $ | (12) |
权的基本定义为:
| $ P = \frac{{\sigma _0^2}}{{{\sigma ^2}}} $ | (13) |
式中,σ02为任意常数,目前常取σ02=1,则可推导出高度角定权基本表达式为:
| $ P = {\sin ^2}\left( {{\rm{elv}}} \right) $ | (14) |
大地测量数据处理中用绝对精度指标和相对精度指标来衡量观测值或参数估计的不确定性。其中,方差和中误差能够表征待估参数的离散程度,是误差随机波动性的度量,可以反映观测值或参数估值的不确定性。但在实际中,由于真值未知,方差(中误差)本身在计算中就存在不确定性。在数量统计中,变异系数也称为标准差率,是标准差与平均值的比值,也是衡量数据离散程度大小的绝对值,能够用来描述和度量随机变量的不确定性[12-13]。此外,变异系数在描述随机变量的不确定性时,具有不依赖于任何先验主观假设的明显优势[14-15]。经典测量数据理论针对不同的观测条件给定不同的定权方法,这些方法实际上都是以式(13)为依据,即利用表征精度绝对数字指标之一的方差来确定表征相对精度的数字指标。考虑到变异系数与标准差的关系,本文提出变异系数赋权法来构造相对精度的数值指标,即观测权重。
设观测值个数为n,影响参数估计的质量指标个数为m,则构造指标矩阵X=[xij]m×n(i=1, 2, …, n;j=1, 2, …, m),则变异系数计算公式为:
| $ V = \frac{{{\sigma ^2}}}{{\bar x}} $ | (15) |
式中,V为指标的变异系数,也称为标准差系数,σ2为指标的标准差,x为指标的平均值。标准差与平均值具体算式为:
| $ \begin{array}{*{20}{c}} {\bar x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} }\\ {{\sigma _j} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} } ,i = 1,2, \cdots ,n} \end{array} $ | (16) |
定义各项指标的权重w为:
| $ w = \frac{V}{{\mathit{\Sigma }{V_i}}} $ | (17) |
计算观测值的权重值:
| $ \mathit{\boldsymbol{H}} = b\mathop {\mathit{\boldsymbol{q}}}\limits_{n \times m} \times \mathop {\mathit{\boldsymbol{w}}}\limits_{m \times 1} ,\mathit{\boldsymbol{P}} = {\rm{diag}}\left( \mathit{\boldsymbol{H}} \right) $ | (18) |
式中,H为观测值对应的权重值,n为观测值的个数,b为选取的基数值。指标矩阵中各个元素出现的概率公式为:
| $ {q_{ij}} = \frac{{{x_{ij}}}}{{\sum\limits_{j = 1}^m {{x_{ij}}} }} $ | (19) |
由式(7)可知,相位平滑值、卫星高度角都能影响参数估计的质量,称为参数估计的质量指标。本文将高度角(单位rad)的平方和相位平滑值联合构造指标矩阵,通过变异系数赋权法获取观测值的权。图 1为变异系数赋权法计算观测值权的流程。

|
图 1 变异系数赋权计算观测值权的流程 Fig. 1 Flowchart of calculating the weight of observing values by variation coefficient weighting |
高度角定权法和变异系数赋权法实质上都是基于表征绝对精度的指标来确定表征相对精度的指标“权”,不同的是,高度角定权法是根据卫星的高度角来确定观测量的先验方差,而变异系数赋权法则是通过参数估计的质量指标,即卫星高度角、相位平滑值来确定观测量的先验方差。从定权的先决条件而言,高度角定权法是一种主观定权方法,即高度角越高,权重越高;而变异系数赋权法是一种客观定权方法,获取指标的概率分布后,联合变异系数来确定观测值的权。变异系数赋权法相对于高度角定权法而言,顾及观测值多种随机影响因素,具有较强的数学理论基础,在一定程度上排除了专家意见等主观因素的影响。
3 实验分析本实验选取2016-07-02~08(doy184~190)中国境内的IGS站双频观测数据。为避免多路径影响,卫星截止高度角选择15°,数据采样间隔为30 s,电离层单层模型高度选为H=350 km,区域模型选择4阶球谐函数模型。基于实时平滑处理相位平滑数据,分别选取高度角定权法和变异系数赋权法参与平差解算,统计每颗卫星的内符合精度、外符合精度和7 d内的标准差来评估模型的拟合精度、参数估计精度和稳定性。
设4阶球谐函数模型计算天顶方向的总电子含量为VTEC1,相位平滑伪距模型计算天顶方向的总电子含量为VTEC2,则拟合残差Δ=VTEC1-VTEC2,统计卫星的拟合残差作为检验的内符合精度:
| $ \gamma = \sqrt {\frac{{\left[ {\Delta \Delta } \right]}}{n}} $ | (20) |
式中,n为卫星的观测历元数。
表 1(单位TECu)给出BJFS、CHAN和WUHN站的内符合精度统计,其中PIN为卫星编号,G-P为高度角定权法,B-P为变异系数赋权法。由表 1可知,采用变异系数赋权法计算的模型拟合精度优于高度角定权法,而模型拟合精度与测站位置和观测数据有关,同一时刻采用相同数据对于同颗卫星的拟合仅与测站位置有关。换言之,电离层周日变化越平稳的地区,其拟合精度越好,即WUHN站低于BJFS站低于CHAN站。其原因是地球的高、中和低纬度的电离层周日变化都有不同的特点,特别是在赤道附近和两极地区,电离层周日变化剧烈,电离层区域模型拟合精度受其影响较大。同一纬度同一测站相比而言,数据越充足模型拟合精度越好。
|
|
表 1 BJFS、CHAN和WUHN站内符合精度统计 Tab. 1 Comparison of accuracy at BJFS, CHAN and WUHN stations |
选取IGS网站提供的硬件延迟作为真值,评价2种定权方法参数估计的精度。设IGS提供的硬件延迟值为dŝ,计算残差为v=dŝ-ds,则定义外符合精度为:
| $ {\sigma _{外}} = \sqrt {\frac{{\left[ {vv} \right]}}{r}} $ | (21) |
式中,r为卫星的个数。
图 2为高度角定权法和变异系数赋权法计算的GNSS-DCB残差对比。由图可知,采用高度角定权法计算残差最高为-5.777 4 ns,采用变异系数赋权法计算残差最高为-4.450 9 ns,其主要原因是区域测站少且分布不均匀。采用稀疏站建模过程中由于部分观测数据较少,2种定权方法在估计参数精度时个别卫星结果恰好与原先猜想相反,即高度角定权法的PIN-07、PIN-09、PIN-15、PIN-20和PIN-30单天解残差低于变异系数赋权法。但总体而言,变异系数赋权法参数估计精度优于高度角定权法。为更方便地比较2种定权方法参数估计的精度,分别求取残差的最大值、最小值、平均值、中数和外符合精度进行分析,结果见表 2(单位ns)。
|
|
表 2 2种方法的GNSS-DCB残差精度对比 Tab. 2 Comparison of GNSS-DCB residual accuracy of the two methods |
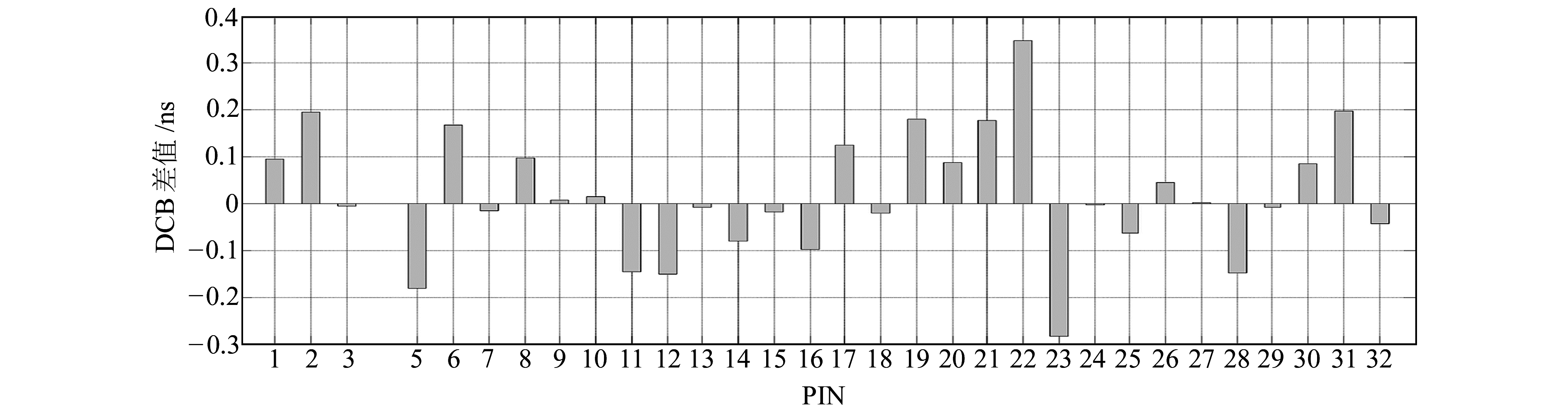
由表 2可知,高度角定权法参数估计残差最小值为0.037 0 ns,平均残差为0.256 6 ns,残差中数为0.037 0 ns;变异系数赋权法参数估计残差最小为0.032 3 ns,平均残差为0.199 1 ns,残差中数为0.032 3 ns。结果表明,2种定权方法及其电离层建模时所涉及的相关参数选取是可靠的。经计算可知,高度角定权法外符合精度为0.286 8 ns,变异系数赋权法外符合精度为0.222 8 ns,变异系数赋权法外符合精度低于高度角定权法。通过残差最大值、最小值、平均值和中数及其外符合精度的对比可知,变异系数赋权法在参数估计的精度方面优于高度角定权法。图 3为变异系数赋权法与高度角定权法的差值对比。由图可知,单天数据采用变异系数赋权法和高度角定权法参与平差解算的GNSS-DCB最大差异为0.25 ns。由图 2、3和表 2综合分析可知,单天数据采用变异系数赋权法相对于高度角定权法参数估计精度最大能提高0.2 ns。

|
图 2 2种方法的GNSS-DCB残差对比 Fig. 2 Comparison of GNSS-DCB residual difference of the two methods |
统计一个周内的标准差来作为稳定性评估的指标。公式如下:
| $ {\rm{ST}}{{\rm{D}}^j} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{\rm{d}}{s^{i,j}} - {\rm{d}}{{\bar s}^{i,j}}} \right)}^2}} }}{{n - 1}}} ,i = 1,2, \cdots ,n $ | (22) |
式中,STDj为第j颗卫星DCB估值的稳定性,dsi, j为第i天计算得到的第j颗卫星DCB的日估值,dsi, j为第j颗卫星DCB的周均值,n为统计的总天数。
|
图 3 2种方法差值对比 Fig. 3 Comparison of difference of the two methods |
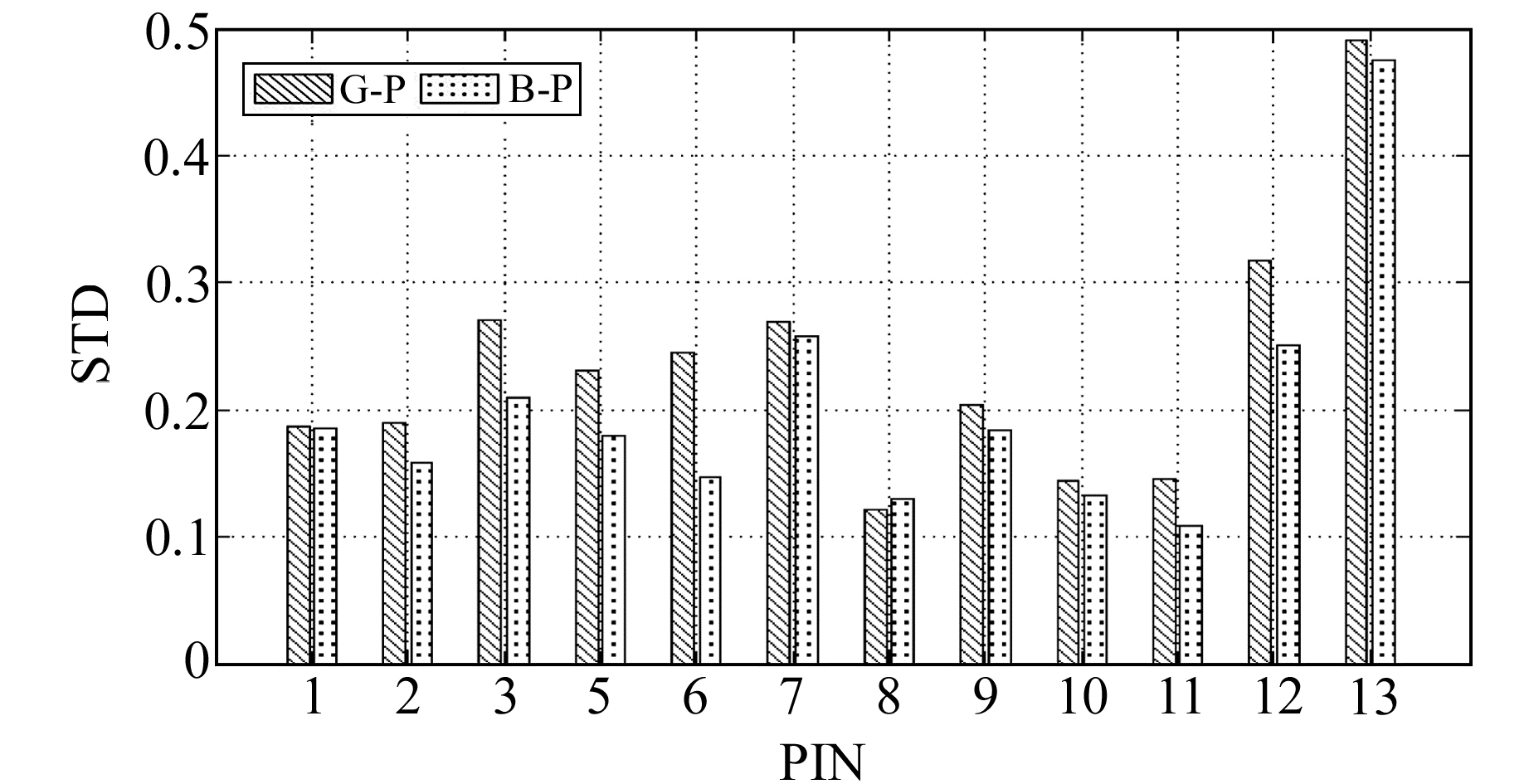
由图 4可知,PIN-13卫星7 d内的稳定性最差,原因是采用区域测站少且分布不均匀。但总体而言,各卫星的拟合精度较好,且变异系数赋权法在参数估计的稳定性方面优于高度角定权法。为进一步分析参数估计的有效性,统计单位权方差(后验方差)并进行分析,结果见表 3。可以看出,2种定权方法平差精度相差不大,变异系数赋权法的平差精度总体优于高度角定权法。
|
图 4 2种方法2016年doy 184~190GNSS-DCB的稳定性 Fig. 4 Stability of GNSS-DCB of the two methods during doy 184 to 190 of 2016 |
|
|
表 3 不同测站不同卫星2种方法平差精度统计 Tab. 3 Comparison of the adjustment accuracy of the two methods for different satellites and different measuring stations |
本文针对目前经验定权随机模型的不足,基于实时去噪和码、相位观测数据的实时加权联合处理思想,提出一种更客观的观测权分配方法,即变异系数赋权法。该方法具有较严密的数学理论基础,能够顾及观测值多种随机因素的影响,提高GNSS-DCB的解算精度。实验结果表明,采用变异系数赋权法计算的模型拟合精度优于高度角定权法;模型的拟合精度与测站位置和观测数据有关,测站位置电离层7 d变化越平稳,观测数据越充足,则模型拟合精度越好。变异系数赋权法在参数估计的精度和稳定性方面优于高度角定权法,单天GNSS-DCB的计算精度提高0.2 ns;不同随机模型对参数估计的影响精度在0.25 ns以内。本文验证变异系数赋权法针对小区域范围内估计GNSS-DCB的效果较好,但较大区域范围的适用性仍需进一步研究。另外,该方法对于GNSS高精度导航定位随机模型的探讨也有很好的参考价值。
| [1] |
叶晓舟, 陈鹏, 吴寒. 不同定权方式对VTEC计算结果的影响[J]. 大地测量与地球动力学, 2010, 30(6): 105-107 (Ye Xiaozhou, Chen Peng, Wu Han. Results of VTEC Influenced by Different Weighting Methods[J]. Journal of Geodesy and Geodynamics, 2010, 30(6): 105-107)
(  0) 0) |
| [2] |
王永弟, 许承权. 熵权理论在测量平差中的应用[J]. 测绘通报, 2012(11): 52-54 (Wang Yongdi, Xu Chengquan. Application of Enteopy Theory in Measurement Adjustment[J]. Bulletin of Surveying and Mapping, 2012(11): 52-54)
(  0) 0) |
| [3] |
张小红, 何锡扬, 李星星. TriP软件非差几何法精密定轨精度分析[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1327-1330 (Zhang Xiaohong, He Xiyang, Li Xingxing. Analysis of Undifferenced Kinematic POD for LEOs Using TriP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1327-1330)
(  0) 0) |
| [4] |
王永弟, 许承权, 范千. 熵权、变异系数及模糊多准则决策在测量平差中的综合应用[J]. 工程勘察, 2012, 40(9): 58-61 (Wang Yongdi, Xu Chengquan, Fan Qian. Integrated Application of Entropy Theory, Variation Coefficient and Fuzzy Multi-Criteria Decision Making in Surveying Adjustment[J]. Geotechnical Investigation and Surveying, 2012, 40(9): 58-61)
(  0) 0) |
| [5] |
舒宝, 刘晖, 张明, 等. 北斗系统硬件延迟解算及精度分析[J]. 武汉大学学报:信息科学版, 2016, 41(2): 279-284 (Shu Bao, Liu Hui, Zhang Ming, et al. Evaluation and Analysis of BDS Instrumental Biases[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 279-284)
(  0) 0) |
| [6] |
Jiao W H, Geng C J, Ma Y H, et al. A Method to Estimate DCB of COMPASS Satellites Based on Global Ionosphere Map[C]. China Satellite Navigation Conference, Guangzhou, 2012
(  0) 0) |
| [7] |
谢益炳, 陈俊平, 伍吉仓, 等. 不同约束条件对电离层电子含量和硬件延迟的影响[J]. 武汉大学学报:信息科学版, 2014, 39(7): 799-803 (Xie Yibing, Chen Junping, Wu Jicang, et al. Ionospheric Electron Content and Hardware Delay Analysis Based on Different Constraints[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 799-803)
(  0) 0) |
| [8] |
雷伟伟, 张捍卫, 李凯. 完全规格化缔合勒让德函数常用递推算法的适用性[J]. 大地测量与地球动力学, 2016, 36(5): 386-390 (Lei Weiwei, Zhang Hanwei, Li Kai. Applicability Analysis for the Common Recursive Algorithms of Fully Normalized Associated Legendre Function[J]. Journal of Geodesy and Geodynamics, 2016, 36(5): 386-390)
(  0) 0) |
| [9] |
高成发, 赵毅, 万德钧. GPS载波定位中双差观测值权的合理确定[J]. 测绘科学, 2005, 30(3): 28-32 (Gao Chengfa, Zhao Yi, Wan Dejun. The Weight Determination of the Double Difference Observation in GPS Carrier Phase Positioning[J]. Science of Surveying and Mapping, 2005, 30(3): 28-32 DOI:10.3771/j.issn.1009-2307.2005.03.007)
(  0) 0) |
| [10] |
何海波, 杨元喜. GPS观测量先验方差-协方差矩阵实时估计[J]. 测绘学报, 2001, 30(1): 42-47 (He Haibo, Yang Yuanxi. Real-Time Estimation of a Prior Variance-Covariance for GPS Observations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 42-47 DOI:10.3321/j.issn:1001-1595.2001.01.009)
(  0) 0) |
| [11] |
张守建, 李建成, 邹贤才, 等. GRACE卫星精密定轨随机模型精化[J]. 地球物理学报, 2010, 53(7): 1554-1561 (Zhang Shoujian, Li Jiancheng, Zou Xiancai, et al. The Stochastic Model Refinement for Precise Orbit Determination of GRACE[J]. Chinese Journal of Geophysics, 2010, 53(7): 1554-1561 DOI:10.3969/j.issn.0001-5733.2010.07.006)
(  0) 0) |
| [12] |
周访滨.测量数据误差分布的熵及其应用研究[D].长沙: 中南大学, 2014 (Zhou Fangbin. Entropy of Surveying Data Error Distribution and Application[D]. Changsha: Central South University, 2014)
(  0) 0) |
| [13] |
白礼虎.基于模糊互补判断矩阵和直觉模糊熵的决策研究[D].合肥: 安徽大学, 2013 (Bai Lihu. The Decision-Making Research Based on the Fuzzy Complementary Judgment Matrix and Intuitionistic Fuzzy Entropy[D]. Hefei: Anhui University, 2013)
(  0) 0) |
| [14] |
门宝辉, 赵燮京, 梁川. 基于变异系数权重的水质评价属性识别模型[J]. 郑州大学学报:理学版, 2003, 35(3): 86-89 (Men Baohui, Zhao Xiejing, Liang Chuan. Attribute Recognition Model for Evaluating Water Quality[J]. Journal of Zhengzhou University: Natural Science Edition, 2003, 35(3): 86-89)
(  0) 0) |
| [15] |
石宝峰, 程砚秋, 王静. 变异系数加权的组合赋权模型及科技评价实证[J]. 科研管理, 2016, 37(5): 122-131 (Shi Baofeng, Cheng Yanqiu, Wang Jing. A Combination Empowerment Model Based on Variation Coefficient Weighted and Its Empirical Study of S&T Evaluation[J]. Science Research Management, 2016, 37(5): 122-131)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39

