2. 武汉大学卫星导航定位技术研究中心, 武汉市珞喻路129号,430079
基于GNSS技术探测大气的方法可以分为地基GNSS网层析技术、单站地基GNSS反演技术和空基GNSS掩星技术。地基单站GNSS接收机在定位中能够获取电磁波传播路径的对流层延迟信息,因此可以用来反演对流层大气折射率剖面。与地基GNSS网层析和空基GNSS掩星技术相比,地基单站GNSS技术具有观测成本低、操作简单、可移动性较强等优点[1]。
Lowry等[2]首次提出基于地基单GNSS测站获得的斜路径延迟来反演对流层大气折射率剖面。随后,林乐科等[3-6]对单站地基GNSS探测大气折射率剖面进行深入研究,实现了基于对流层天顶延迟的折射率剖面反演,并在广东东南沿海地区开展单站地基GNSS探测大气的大型观测实验。目前,单站地基GNSS反演大气折射率的模型仍需进一步改进,以提高大气折射率的反演精度。本文提出一种新的利用天顶对流层延迟反演大气折射率的模型,并选用中国及周边区域8个IGS测站的观测数据进行试算。将测站附近探空产品获取的大气折射率作为真值,统计结果显示,与传统的反演模型相比,新的反演模型提高了大气折射率的反演精度。
1 传统的基于天顶对流层延迟的模型参数反演利用平差模型,通过GNSS接收机接收到的电磁波信号可以估算出测站的坐标、天顶对流层延迟(ZTD)、接收机钟差等信息。天顶对流层延迟在导航和定位中是一种主要的误差源,而在GNSS气象学中,它却是一种探测对流层大气的信号源[7-8],根据是否含有水汽,可划分为天顶对流层干延迟(ZHD)和天顶对流层湿延迟(ZWD)[9]。实际的反演中,根据不同的模型利用ZHD和ZWD分别反演出大气干折射率NT和大气湿折射率NW。
1.1 干项模型参数估计干项大气折射率比较稳定,近似认为满足大气静力平衡,Hopfield[10]推导获得满足大气静力平衡时的干项大气折射率为:
| $ N_T^h \approx N_T^{{h_0}}{\left( {\frac{{{T_0} + \beta h}}{{{T_0}}}} \right)^{ - \left( {1 + \frac{g}{{\beta {R_d}}}} \right)}} $ | (1) |
式中, NTh0为地面折射率静力项,T0为地面温度(K),h为相对于地面站的高度,β为高度方向的温度梯度,g为重力加速度(一般变化不大),Rd为干空气的比气体常数。
ZHD可表示为干项折射率的积分[11]:
| $ {\rm{ZHD}} = {10^{ - 6}}\int_{{h_0}}^{{H_h}} {N_T^h} (h){\rm{d}}h $ | (2) |
由式(2)便可估算出折射率干项在对流层HTro内的积分[11]:
| $ \begin{array}{*{20}{c}} {{\rm{ZH}}{{\rm{D}}^{{\rm{Tro}}}} = {{10}^{ - 6}}\int_0^{{H_{{\rm{Tro}}}}} {N_T^h} (h){\rm{d}}h = }\\ {{{10}^{ - 6}}N_T^{{h_0}}\frac{{{{\left( {{T_0} + \beta {H_{{\rm{Tro}}}}} \right)}^{\eta + 1}} - T_\delta ^{\eta + 1}}}{{(\eta + 1)T_0^\eta \beta }}} \end{array} $ | (3) |
式中,
由式(3)可以估算出β,将其代入式(1)便可得到不同高度层的大气折射率干项。
1.2 湿项模型参数估计从ZTD中剔除ZHD便可得到ZWD[10]:
| $ Z{\rm{WD}} = Z{\rm{TD}} - Z{\rm{HD}} $ | (4) |
ZWD可表示为湿项折射率Nw的积分:
| $ Z{\rm{WD}} = {10^{ - 6}}\int_0^\infty {{N_w}} (h){\rm{d}}h $ | (5) |
Nw随高程呈现近似指数形式的分布[11]:
| $ {N_w}\left( h \right) = N_w^0\exp \left( {\frac{{ - h}}{{{H_{we}}}}} \right) $ | (6) |
式中,Hwe为湿项的特征高度,Nw0为起始高度处的湿项折射率。
根据式(5)和式(6)可知[11]:
| $ Z{\rm{WD}} = {10^{ - 6}}{H_{we}}N_w^0 $ | (7) |
通过式(7)可估算出Hwe,将其代入式(6)可计算出不同高程处的湿折射率。
2 新的基于天顶对流层延迟的模型参数反演 2.1 新的干项模型参数估计干项折射率随高程的变化比较平稳,根据式(1)和式(3),在获取ZHD和HTro后,利用搜索的方法便可计算出β,将其代入式(1)便可获得不同高度层的NTh。通常情况下,GNSS测站会配置气象观测文件,能够提供压强、温度和相对湿度。基于压强信息,利用Saastamoinen模型可以精确地估算出ZHD。HTro随区域和季节的变化不断改变,而传统上HTro通常取一个经验值60 km。本文试图基于Era-Interim产品估算HTro。
ERA-Intrim提供了不同高程上的压强、温度、湿度等气象产品,利用这些产品可以计算出不同高程上的大气干项折射率及ZHD:
| $ N_T^h = 77.6 \cdot \frac{{{P_h}}}{{{T_h}}} $ | (8) |
| $ {\rm{ZH}}{{\rm{D}}_h} = \frac{{{{10}^{ - 6}} \cdot \sum\limits_{i = 0}^{i = n - 1} {\left( {N_T^{{h_i}} + N_T^{{h_{i + 1}}}} \right)} }}{2} $ | (9) |
将起始高度的ZHDh(即ZHD1)视为总的天顶干延迟,而不同高程h上估算的ZHDh占ZHD1的比例为RZHD:
| $ {\rm{RZH}}{{\rm{D}}_h} = \frac{{{\rm{ZH}}{{\rm{D}}_h}}}{{{\rm{ZH}}{{\rm{D}}_1}}} $ | (10) |
若高程h上RZHD小于等于0.01,则定义h所对应的高度为HTro。
2.2 新的湿项模型参数估计研究无线探空、无线掩星等高垂直分辨率、高精度的气象观测值发现,Nhw与Pwh之间的关系可近似表示为:
| $ \left( {\frac{{N_h^w}}{{N_{{h_0}}^w}}} \right) = {\left( {\frac{{P_w^h}}{{P_w^{{h_0}}}}} \right)^\gamma } = {\left( {\frac{{{T_0} + \beta \left( {h - {h_0}} \right)}}{{{T_0}}}} \right)^{\frac{{\gamma {g_0}}}{{\beta {R_d}}}}} $ | (11) |
式中,γ为大气混合比指数。
通过式(5)可知:
| $ \begin{array}{*{20}{c}} {Z{\rm{WD}} = {{10}^{ - 6}} \cdot N_{{h_0}}^w\int_0^\infty {{{\left( {\frac{{{T_0} + \beta \left( {h - {h_0}} \right)}}{{{T_0}}}} \right)}^\gamma }} {\rm{d}}h = }\\ {{{10}^{ - 6}} \cdot N_{{h_0}}^w \cdot \frac{{{T_0}\left( {E + 1} \right)}}{\beta } \cdot }\\ {\left[ {1 - {{\left[ {\frac{{{T_0} + \beta \left( {{H_{{\rm{top}}}} - {h_0}} \right)}}{{{T_0}}}} \right]}^{\left( {E + 1} \right)}}} \right]} \end{array} $ | (12) |
式中,
选择中国及周边区域8个IGS站(图 1)2016-07的观测数据及气象观测值,使用Bernese5.2软件及IGS事后轨道产品和钟差产品,卫星截止高度角设置为7°,然后选用精密单点定位的计算模型估算ZTD。基于Saastamoinen模型可以获得ZHD[12],然后从ZTD中分离出ZWD。
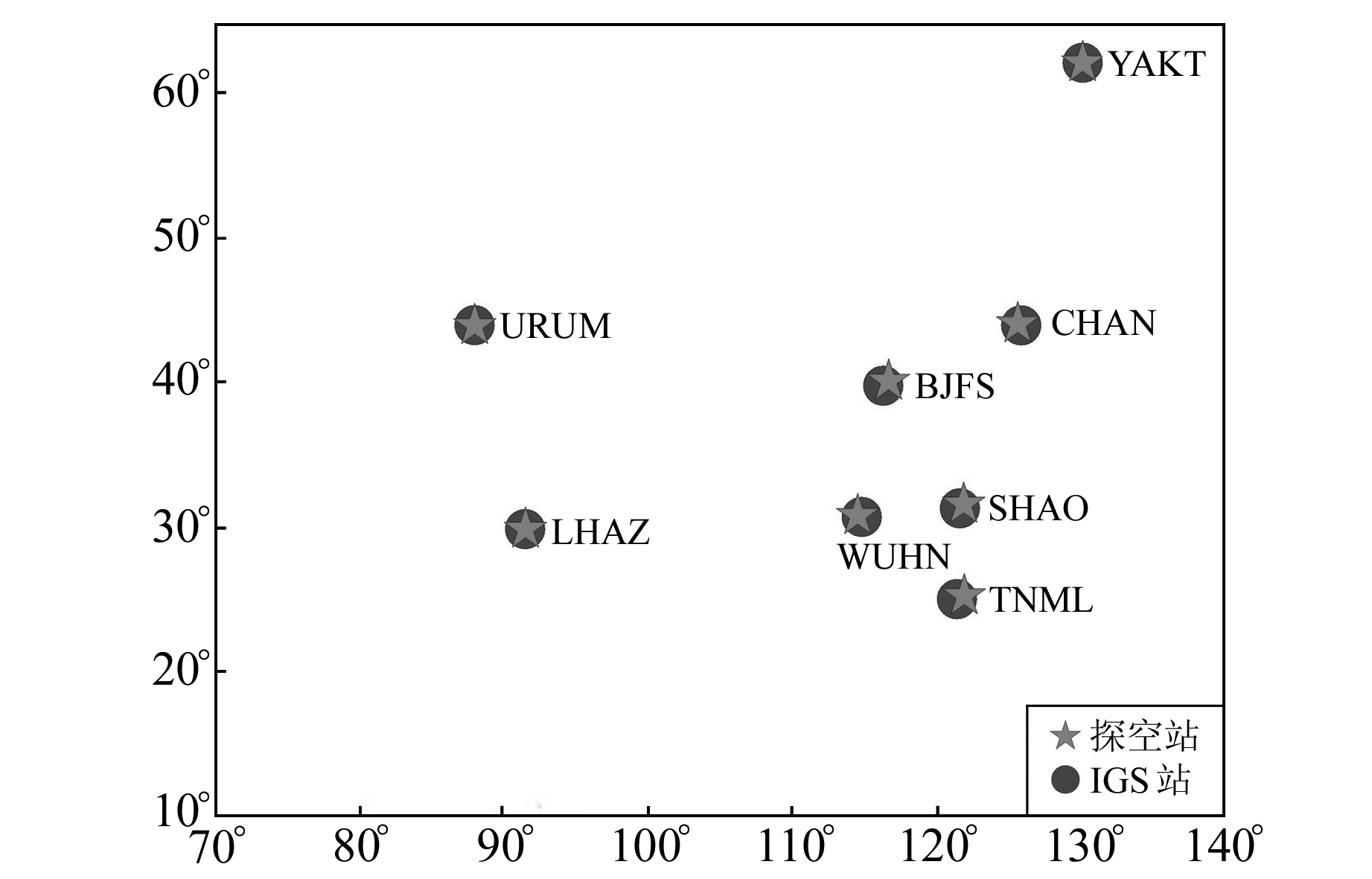
|
图 1 所选取的8个IGS测站及附近探空测站分布 Fig. 1 Distribution of the selected eight IGS stations and nearby radiosonde stations |
Era-Interim提供高垂直分辨率的大气压强、大气温度和湿度等大气产品,可从网站http://apps.ecmwf.int/datasets/data/interim-full-daily/下载。选择中国地区2006~2016-07的Era-Interim产品,分别利用式(10)和MWO方法估算出HTro和Htop,最后分别利用传统和新的模型参数反演出大气折射率。表 1给出中国及周边区域8个IGS测站2016-07的HTro和Htop。
|
|
表 1 8个IGS测站2016-07的HTro和Htop Tab. 1 HTro and Htop of eight IGS staions in July, 2016 |
从表 1看出,不同地区的HTro最大差距为16 km,而Htop的最大差距为5.09 km;LHAZ和URUM站等偏干旱区域的HTro和Htop要小于偏湿润的TNML站。
3.3 反演结果与探空数据的比较从图 1中可以看出,每一个IGS测站附近都有一个探空测站,每天提供2次探测结果。探空数据可以提供高精度的、随高程变化的大气参数,如温度、压强、相对湿度和混合比等。利用探空产品获得的对流层折射率作为真值来检验本文方法获得的结果。图 2和图 3分别给出URUM和WUHN站单个反演剖面的结果。
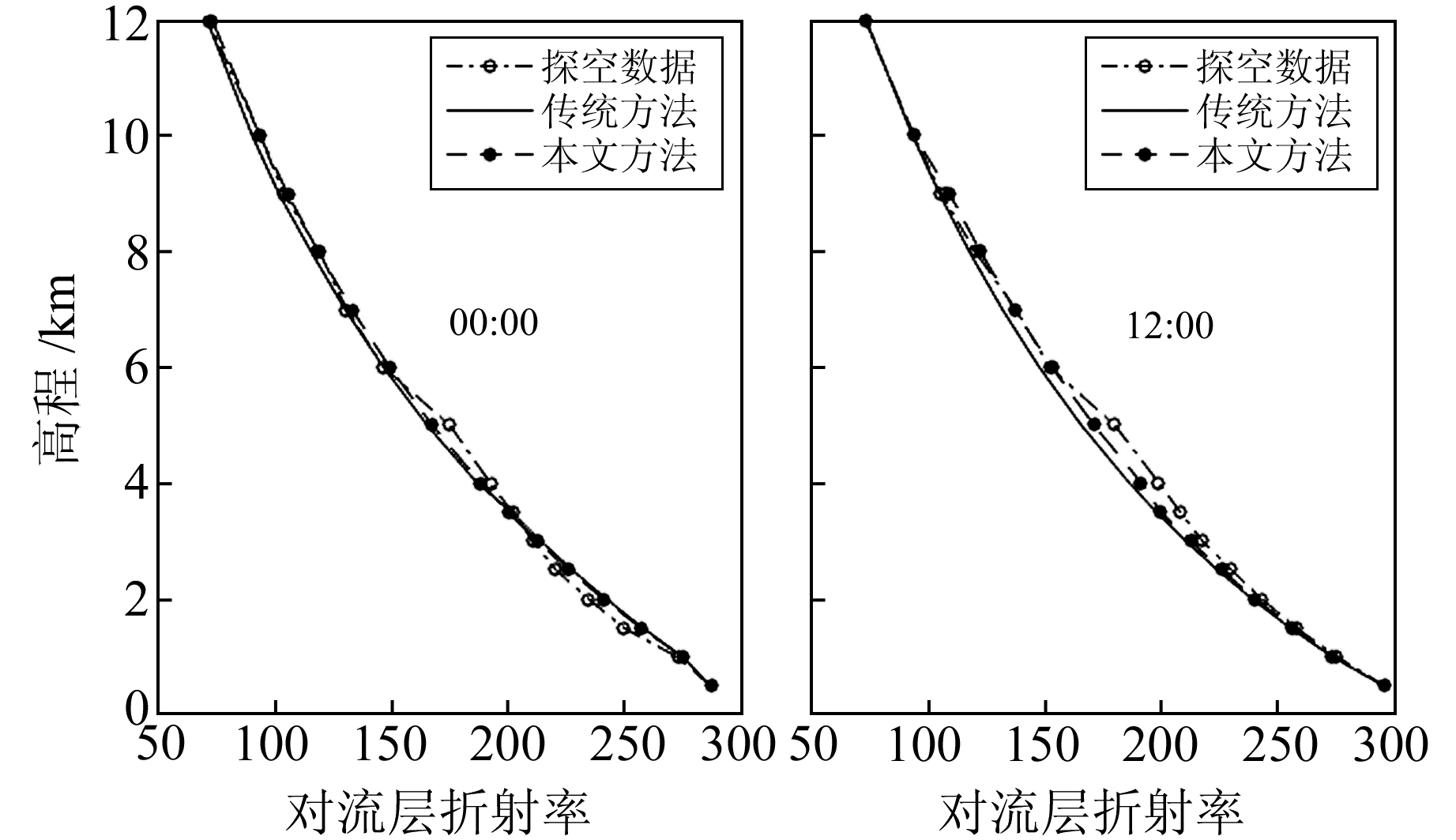
|
图 2 URUM站2016年第183天反演结果 Fig. 2 The inversion at URUM station on doy 183 of 2016 |
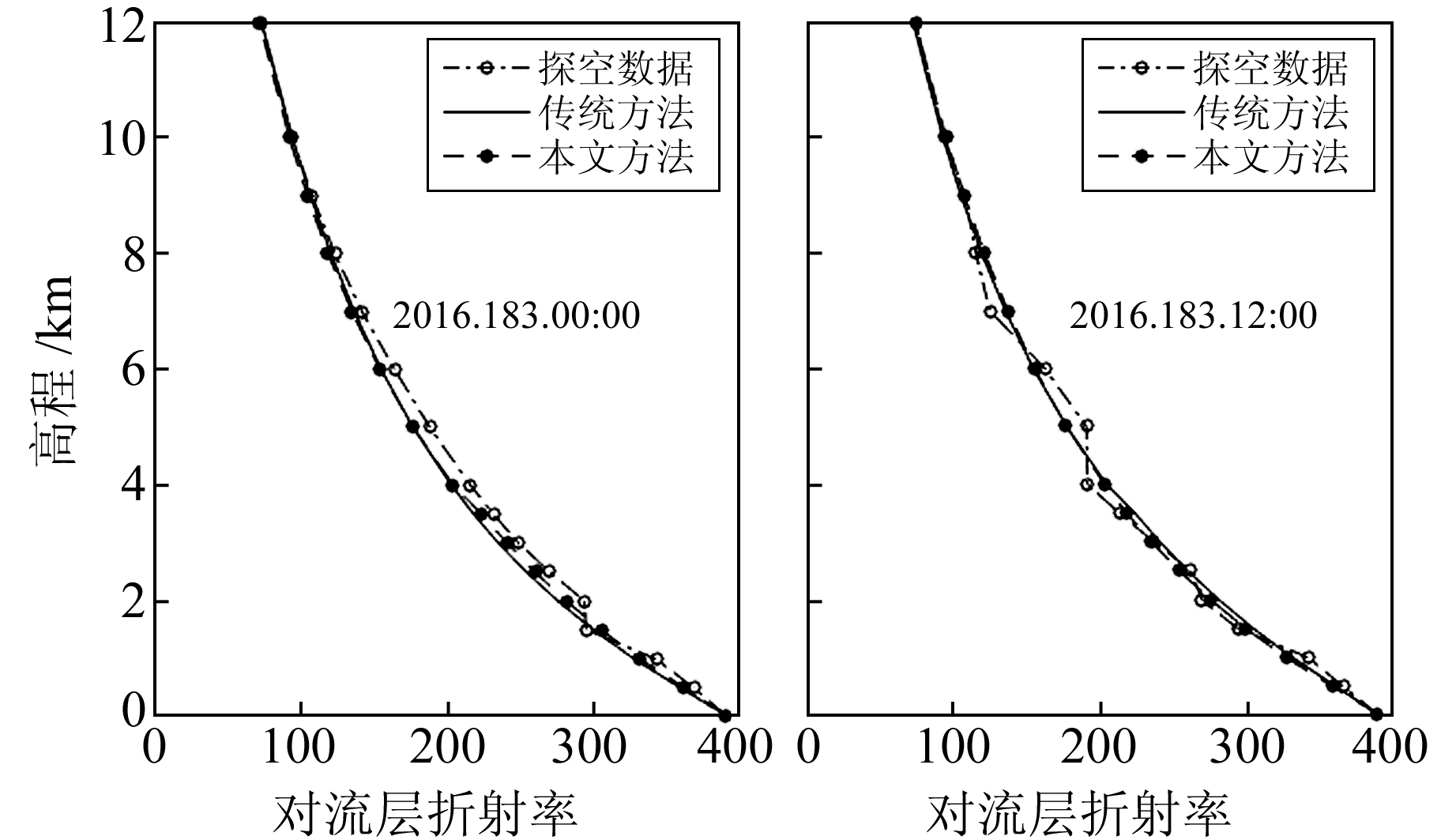
|
图 3 WUHN站2016年第183天反演结果 Fig. 3 The inversion at WUHN station on doy 183 of 2016 |
从图 2和图 3可以看出,与传统的模型参数法反演的大气折射率相比,新的模型参数法反演的大气折射率更接近真值。当大气折射率在空间分布中存在“逆增层”现象时,新的模型参数法及传统的模型参数法反演的结果与真值存在较大的偏差。此外,给出2个测站模型参数法获得的结果与真值之间1个月的偏差分布图(图 4、5)。
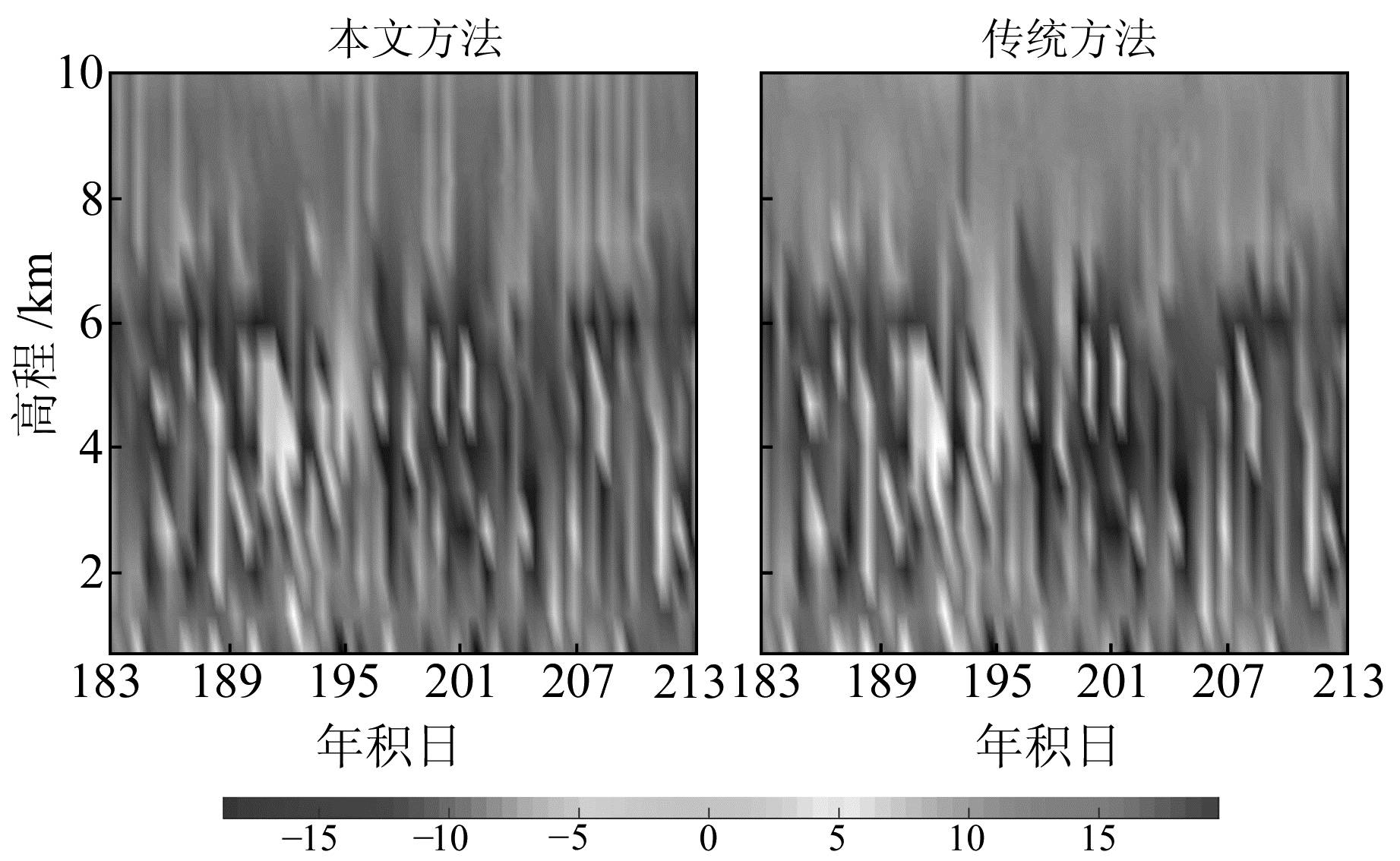
|
图 4 URUM站2016-07模型参数反演结果与真值的偏差 Fig. 4 The deviation of inversion between model-derived and true values at URUM station in July 2016 |
|
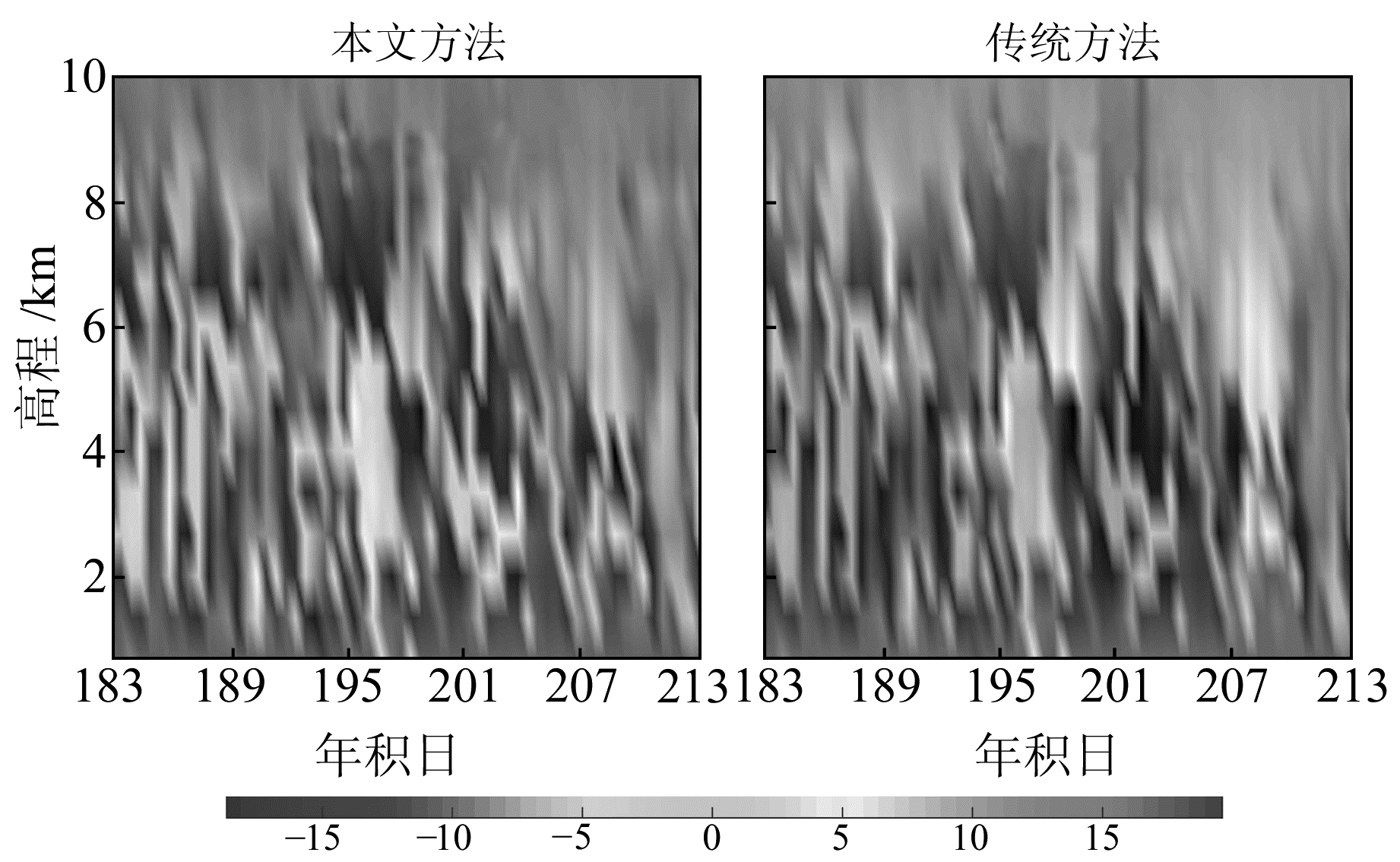
图 5 WUHN站2016-07模型参数反演结果与真值的偏差 Fig. 5 The deviation of inversion between model-derived and true values in WUHN station in July 2016 |
图 4、5显示,大部分情况下新的模型参数法反演得到的大气折射率更接近真值。此外,统计8个测站模型参数法获得的结果与真值之间的偏差(表 2)。
|
|
表 2 8个IGS测站模型参数反演的结果与真值之间的偏差 Tab. 2 The statistical values of deviation between model-derived and true values at the eight IGS stations |
从表 2可以看出,新的模型参数法获得的结果更接近真值,从而证实了其有效性。
4 结语GNSS气象学使得对流层延迟成为反演大气参数的有效信号源。本文利用天顶对流层延迟值,基于模型参数法反演不同高程处的大气折射率,并利用探测产品获得的大气折射率作为真值来评估新的模型参数法的可行性。选择中国及周边地区8个IGS测站2016-07的观测数据进行试算,结果显示,与传统的模型参数法反演的结果相比,新的模型参数法反演的大气折射率更接近真值。然而,当大气折射率的空间分布中存在“逆增层”现象时,2种模型参数法获得的结果都与真值存在较大的偏差。如何反演大气折射率“逆增层”现象将是下一步重点研究的内容。
| [1] |
林乐科, 张业荣, 赵振维, 等. 基于支持向量机的地基单站GPS反演大气剖面[J]. 南京邮电大学学报:自然科学版, 2009, 29(4): 64-68 (Lin Leke, Zhang Yerong, Zhao Zhenwei, et al. Retrieving Atmospheric Profiles Based on Support Vector Machine and Singular Ground-Based GPS Receiver[J]. Journal of Nanjing University of Posts and Telecommunications:Natural Science, 2009, 29(4): 64-68)
(  0) 0) |
| [2] |
Lowry A R, Rocken C, Sokolovskiy S V, et al. Vertical Profiling of Atmospheric Refractivity from Ground-Based GPS[J]. Radio Science, 2002, 37(3): 1-21
(  0) 0) |
| [3] |
林乐科, 张业荣, 赵振维, 等. 基于天顶湿延迟的GPS大气折射率剖面反演研究[J]. 全球定位系统, 2007, 32(3): 1-4 (Lin Leke, Zhang Yerong, Zhao Zhenwei, et al. Study on Retrieving Atmosphere Refractivity Profiles Using Zenith Wet Delay (ZWD) of GPS[J]. GNSS World of China, 2007, 32(3): 1-4 DOI:10.3969/j.issn.1008-9268.2007.03.001)
(  0) 0) |
| [4] |
林乐科, 赵振维, 张业荣, 等. 利用BP-ANN和地基单站GPS数据反演大气折射率剖面[J]. 微波学报, 2008, 24(6): 39-42 (Lin Leke, Zhao Zhenwei, Zhang Yerong, et al. Retrieving Atmospheric Refractivity Profiles Based on Singular Ground-Based GPS Receiver and BP-ANN Network[J]. Journal of Microwaves, 2008, 24(6): 39-42)
(  0) 0) |
| [5] |
林乐科, 张业荣, 赵振维, 等.一种GPS大气折射率剖面统计反演方法[C].第9届全国电波传播学术讨论会, 西安, 2007 (Lin Leke, Zhang Yerong, Zhao Zhenwei, et al. A GPS Method for Statistical Inversion of Atmospheric Refractive Profile[C].The 9th Chinese National Symposium on Radio Propagation, Xi'an, 2007)
(  0) 0) |
| [6] |
Lin L K, Zhao Z W, Zhang Y R, et al. Tropospheric Refractivity Profiling Based on Single Ground-Based GPS[C]. International Conference on Microwave and Millimeter Wave Technology, Nanjing, 2008
(  0) 0) |
| [7] |
夏朋飞, 蔡昌盛, 戴吾蛟, 等. 地基GPS联合COSMIC掩星数据的水汽三维层析研究[J]. 武汉大学学报:信息科学版, 2013, 38(8): 892-896 (Xia Pengfei, Cai Changsheng, Dai Wujiao, et al. Three-Dimensional Water Vapor Tomography Using Ground-Based GPS and COSMIC Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 892-896)
(  0) 0) |
| [8] |
夏朋飞, 叶世榕. 一种基于组合重构算法的对流层层析技术[J]. 大地测量与地球动力学, 2017, 37(9): 928-932 (Xia Pengfei, Ye Shirong. A Troposphere Tomography Technique Based on Combined Reconstruction Algorithm[J]. Journal of Geodesy and Geodynamics, 2017, 37(9): 928-932 DOI:10.14075/j.jgg.2017.09.011)
(  0) 0) |
| [9] |
叶世榕, 江鹏, 刘炎炎. 地基GPS网层析水汽三维分布数值积分方法[J]. 测绘学报, 2013, 42(5): 654-660 (Ye Shirong, Jiang Peng, Liu Yanyan. A Water Vapor Tomographic Numerical Quadrature Approach with Ground-Based GPS Network[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 654-660)
(  0) 0) |
| [10] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical research, 1969, 74(18): 4487-4499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [11] |
林乐科.利用GNSS信号的地基大气折射率剖面反演技术研究[D].南京: 南京邮电大学, 2011 (Lin Leke. Profiling Tropospheric Refractivity Based on Single Ground-Based GPS Receiver[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2011)
(  0) 0) |
| [12] |
Saatamoinen J. Atmospheric Correction for Troposphere and Stratosphere in Radio Ranging of Satellites[J]. Geophys Monogr Ser, 1972, 15: 247-251 DOI:10.1029/GM015p0247
(  0) 0) |
| [13] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1973, 107(1): 13-34 DOI:10.1007/BF02522083
(  0) 0) |
2. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39


