快速沉降区域(如采矿塌陷区)不同于大坝等沉降缓慢、稳定的区域,其运动情形很难用统一的动力学模型进行描述,而过分依赖于有误差的动力学模型会导致滤波结果出现较大的误差,甚至滤波发散。同时,在设备自动化采集数据过程中,难免会产生各种粗差,这些粗差会对滤波结果造成毁灭性的影响,滤波结果将严重偏离真实值。有学者提出多种自适应滤波与抗差滤波的方法,如方差补偿自适应滤波[1]、多衰减因子自适应滤波[2]、移动开窗估计滤波[3]等自适应滤波,将抗差理论与卡尔曼滤波相结合的抗差卡尔曼滤波[4]和秩亏观测模型的抗差卡尔曼滤波[5],以及三段函数模型[6]、选权函数模型[7]等抗差自适应卡尔曼滤波方案,这些滤波方案能较好地平衡动力学模型预测向量与观测向量对滤波结果的贡献,但在观测对象的状态发生快速变化时,滤波结果会出现较大的误差。
本文针对快速沉降区域所具有的沉降量大、突发性强、局部时间稳定沉降等动力学特点及观测过程存在粗差等情况,设计一种抗差自适应卡尔曼滤波模型,能识别稳定沉降与快速沉降2种状态,采用抗差估计对观测向量中的粗差进行有效削弱,并采用自适应因子调整动力学模型对滤波值的影响,以减少状态模型的误差,提高滤波结果的精度。通过实例验证,该模型能有效减弱模型误差与观测异常对滤波结果的影响,并在发生快速沉降时保持较高的精度。
1 地表快速沉降动力学模型与测量方程的建立地表快速沉降区域的运动状态一般分为2种:1)短时间内地表突发大量沉陷;2)长时间、稳定的沉陷。动力学模型的建立基于稳定沉降状态,地表沉降的程度较小、动态性不大时,可以采用常速度模型,将地表监测点的沉降位移和沉降速度作为状态向量, 则运动状态可以表示为:
| $ \left[ {\begin{array}{*{20}{c}} {{X_k}}\\ {X_k^\prime } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\Delta {t_{k,k - 1}}}\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{k - 1}}}\\ {X_{k - 1}^\prime } \end{array}} \right] + {\mathit{\boldsymbol{\omega }}_k} $ | (1) |
式中,Xk、X′k分别为tk时刻的位移和位移速率,Δtk, k-1为tk至tk-1的时间间隔,ωk为状态模型输入噪声向量。如果将变形加速度Ωk作为随机干扰,则:
| $ {\mathit{\boldsymbol{\omega }}_k} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\Delta t_{k,k - 1}^2}\\ {\Delta {t_{k,k - 1}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{k - 1}} $ | (2) |
监测点的位置信息通过直接测量获得,则观测方程为:
| $ L\left( {{t_k}} \right) = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{X_k}}\\ {X_k^\prime } \end{array}} \right] + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_k} $ | (3) |
如果取Δtk, k-1为单位时间间隔,且系统为线性,则状态转移矩阵Φk, k-1、观测矩阵Ak、状态模型输入噪声矩阵Wk都为定常矩阵,分别为:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,t - 1}} = \left[ {\begin{array}{*{20}{l}} 1&1\\ 0&1 \end{array}} \right],{\mathit{\boldsymbol{A}}_k} = \left[ {\begin{array}{*{20}{l}} 1&0 \end{array}} \right],{\mathit{\boldsymbol{W}}_k} = \left[ {\begin{array}{*{20}{c}} {0.5}\\ 1 \end{array}} \right] $ | (4) |
标准卡尔曼滤波实际为最小二乘滤波解,其要求观测向量与状态预测向量都为高斯白噪声序列。但在实际应用时,观测向量中不可避免地会包含粗差,动力学模型会出现异常,若在数据处理过程中不对这些粗差与异常进行处理,会使卡尔曼滤波估值极不可靠。
2.1 对观测量进行抗差处理 2.1.1 稳定沉降状态采用抗差M估计M估计由极大似然估计推出,Huber将其定义广义化[8],最终得到:
| $ \sum\limits_{i = 1}^n {\frac{{\partial \rho \left( {{\mathit{\boldsymbol{l}}_i},\mathit{\boldsymbol{\hat X}}} \right)}}{{\partial \mathit{\boldsymbol{\hat X}}}}} = 0 $ | (5) |
式中, ρ为任意适当选取的函数。
在测量平差中,观测量L的残差为V,权为P,M估计的ρ函数可取ρ(υi),误差方程为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}} $ | (6) |
则:
| $ {\mathit{\boldsymbol{v}}_i} = {\mathit{\boldsymbol{a}}_i}\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{l}}_i} $ | (7) |
式中,ai为A的第i行向量。
根据式(5)可得:
| $ \sum\limits_{i = 1}^n {\mathit{\boldsymbol{a}}_i^{\rm{T}}} {\mathit{\boldsymbol{P}}_i}\frac{{\rho \left( {{\mathit{\boldsymbol{v}}_i}} \right)}}{{{\mathit{\boldsymbol{v}}_i}}}{\mathit{\boldsymbol{v}}_i} = 0 $ | (8) |
令
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar PV}} = 0 $ | (9) |
由此可以解出参数的M估计:
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\bar PL}} $ | (10) |
式中,P为等价权矩阵,可采用多种方法得到。因IGG法的抗粗差效果更好,且易实现,本文采用IGG法求取权函数,权因子为:
| $ \omega \left( v \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{\left| \mathit{\boldsymbol{v}} \right| < 1.5\sigma }\\ {\frac{1}{{\left| \mathit{\boldsymbol{v}} \right| + k}},}&{1.5\sigma < \left| \mathit{\boldsymbol{v}} \right| < 2.5\sigma }\\ {0,}&{\left| \mathit{\boldsymbol{v}} \right| \le 2.5\sigma } \end{array}} \right. $ | (11) |
在地表快速沉降的观测中,GNSS技术是一种常见的高程监测方法,实际应用中认为各观测历元之间相互独立,则等价权函数为:
| $ {{\mathit{\boldsymbol{\bar P}}}_i} = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\left| \mathit{\boldsymbol{v}} \right| < 1.5\sigma \\ {\mathit{\boldsymbol{P}}_i} \cdot \frac{1}{{\left| \mathit{\boldsymbol{v}} \right| + k}},\;\;\;\;\;1.5\sigma \le \left| \mathit{\boldsymbol{v}} \right| < 2.5\sigma \\ 0,\;\;\;\left| \mathit{\boldsymbol{v}} \right| \ge 2.5\sigma \end{array} \right. $ | (12) |
式中,k为一个相对|v|很小的量,只要在一定范围内,则对估计的效果没有影响[9],本文取0.001。
由式(12)得出等价权矩阵P,代入式(10)得出参数估计值。选定一个微小量ε进行迭代计算,直到第k次与第k-1次迭代所得的参数估计值之差小于ε,即
| $ \left| {{{\mathit{\boldsymbol{\hat X}}}^k} - {{\mathit{\boldsymbol{\hat X}}}^{k - 1}}} \right| \le \varepsilon $ | (13) |
经过多次迭代,能使异常观测的权函数趋于0,最终得到可靠的参数估计
在利用GNSS技术进行沉降监测时,1个监测点上只有1台GNSS设备,即1个历元只能获得1个沉降量,没有多余观测。但因地表处于稳定沉降时,沉降量波动不大,故本文取当前监测期数的沉降量及前1期和后1期沉降量共3期数据进行抗差M估计,所得结果作为当期的沉降量,从而极大削弱了观测误差带来的影响。
2.1.2 快速沉降状态检测与处理在地表处于稳定沉降时,对3期数据进行抗差M估计获得每期的沉降量,但当地表由稳定沉降突入快速沉降时,若依然采用该方法,将会把真实沉降值当作测量粗差, 从而出现误差。因此需要判断每期时刻地表沉降的状态,即判断每期沉降观测量是粗差还是真实快速变形。因监测数据为平稳时间序列,且沉降量存在趋势性变化,本文采用Pettitt检验法[10]进行状态检测并获得状态突变时刻。在突变时刻沉降量不进行抗差估计,直接采用该时刻GNSS监测设备获得的沉降观测量。
假设一长度为n的时间序列xi,i=1, 2, …, n,定义统计量为:
| $ U\left( t \right) = \sum\limits_{i = 1}^t {\sum\limits_{j = t + 1}^n {\rm{sgn}} } \left( {{x_j} - {x_i}} \right),1 \le t \le n $ | (14) |
式中,sgn为符号函数。若时刻t满足:
| $ K = \max \left| {U\left( t \right)} \right| $ | (15) |
则t时刻为突变时刻,同时计算统计量:
| $ P \approx 2\exp \left( {\frac{{ - 6{K^2}}}{{{n^3} + {n^2}}}} \right) $ | (16) |
如果P≤0.5,则认为检测出的突变时刻在统计意义上是显著的。
需要注意的是,Pettitt检验法只能检测到开始突变的时刻,即从稳定沉降状态突入快速沉降状态的时刻,而不能检测到从快速沉降状态回归到稳定沉降状态的时刻,因此需要将时间序列值前后顺序颠倒用于检测从快速沉降状态回归到稳定沉降状态的时刻。
2.2 对状态模型采用自适应因子调节地表快速沉降区域大部分时间都处于稳定沉降的状态,这种状态采用式(1)进行描述即可。但当某一时刻发生大幅度沉降时,之前建立的动力学模型已经无法准确描述当前时刻的状态,状态预测值会出现较大偏差,导致滤波值失真。本文通过选取一个自适应因子,当检测到动力学模型出现较大的误差时,使用自适应因子降低动力学模型预测值对参数估计值的贡献,使滤波结果更多地依赖观测值,从而提高滤波精度。
采用三段自适应因子函数获取自适应因子ak,采用状态不符值统计量
| $ \begin{array}{*{20}{c}} {{a_k} = }\\ {\left\{ {\begin{array}{*{20}{l}} {1,\left| {\Delta {{\mathit{\boldsymbol{\tilde X}}}_k}} \right| \le {c_0}}\\ {\frac{{{c_0}}}{{\left| {\Delta {{\mathit{\boldsymbol{\tilde X}}}_k}} \right|}}{{\left( {\frac{{{c_1} - \left| {\Delta {{\mathit{\boldsymbol{\tilde X}}}_k}} \right|}}{{{c_1} - {c_0}}}} \right)}^2},{c_0} < \left| {\Delta {{\mathit{\boldsymbol{\tilde X}}}_k}} \right| \le {c_1}}\\ {0,\left| {\Delta {{\mathit{\boldsymbol{\tilde X}}}_k}} \right| > {c_1}} \end{array}} \right.} \end{array} $ | (17) |
状态不符值统计量为:
| $ \Delta {{\mathit{\boldsymbol{\tilde X}}}_k} = \left\| {{{\mathit{\boldsymbol{\tilde X}}}_k} - {{\mathit{\boldsymbol{\bar X}}}_k}} \right\|/\sqrt {\rm{tr}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\bar X}_k}}}} \right)} $ | (18) |
式中,
设状态预测向量的误差方程为:
| $ {\mathit{\boldsymbol{V}}_{{{\bar X}_k}}} = {{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} $ | (19) |
观测向量L的误差方程为:
| $ {\mathit{\boldsymbol{V}}_k} = {\mathit{\boldsymbol{A}}_k}{{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{L}}_k} $ | (20) |
为控制预测向量与观测向量的误差并使其最小,构造如下方程:
| $ \mathit{\boldsymbol{V}}_k^{\rm{T}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{V}}_k} + {a_k}\mathit{\boldsymbol{V}}_{{{\bar X}_k}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{{{\bar X}_k}}}{\mathit{\boldsymbol{V}}_{{{\bar X}_k}}} = \min $ | (21) |
对式(21)求极值,并将式(19)和式(20)代入,即可得到状态参数的抗差自适应滤波解:
| $ \mathit{\boldsymbol{\hat X}} = {\left( {\mathit{\boldsymbol{A}}_k^{\rm{T}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{A}}_k} + {a_k}{\mathit{\boldsymbol{P}}_{{{\bar X}_k}}}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{A}}_k^{\rm{T}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{L}}_k} + {a_k}{\mathit{\boldsymbol{P}}_{{{\bar X}_k}}}{{\mathit{\boldsymbol{\bar X}}}_k}} \right) $ | (22) |
式中,PXk为状态预测向量Xk的权矩阵,ak为自适应因子αk,PXk=ΣXk-1。
抗差自适应卡尔曼滤波解算流程见图 1。

|
图 1 滤波解算流程 Fig. 1 Flow chart of filtering solution |
某采煤矿区每日产出的煤绝大部分依靠铁路进行运输,部分铁路线铺设在开采区之上。因矿区不断开采,地下逐渐形成空洞,地表会发生较大的沉降,对于铁路运输来说极其危险,需要对铁路沿线地表进行沉降监测。受火车运行的影响,铁路沿线地表沉降波动较为频繁,且沉降量较大,之前多使用水准仪进行沉降观测,工作量大且观测周期较长。现采用GNSS动态实时测量方法对铁路沿线监测点进行观测,但因动态测量较静态测量的精度低,且观测历元中容易出现粗差,在对数据进行处理时需要采用抗差自适应卡尔曼滤波方法对观测数据进行滤波,以提高精度。
3.1 实验数据及滤波初始值的确定在矿区信号楼楼顶布置1个GNSS基站,在铁路沿线布设4个GNSS自动化监测点(图 2),并进行连续数据采集。将1号自动化监测点采集的数据与水准仪观测计算的数据进行比较,验证设计的抗差自适应卡尔曼滤波在塌陷区数据处理中的可行性。

|
图 2 自动化监测点位置示意图 Fig. 2 Position sketch map of the automatic monitoring points |
为直观地展示设计的抗差自适应卡尔曼滤波的效果,仅选取一段监测期间发生较大沉降的数据进行滤波处理,数据起止时间为2017-07-24~08-08,共15期,取1号自动化监测点每天10:00~11:00的点位高程平均值作为当期监测点的高程,同时将水准仪每日在相同时段观测的沉降位移量作为真值。
取2017-07-20~24水准测量获得的5期沉降位移量作为观测值,设观测为等间隔,位移与位移速率为状态,组成方程进行动态平差,得到初始状态协方差矩阵
分别采用抗差卡尔曼滤波方法与本文方法对15期数据进行滤波处理,得到每期沉降量的滤波值,结果见表 1(单位mm)。
|
|
表 1 2种滤波结果与真值的比较 Tab. 1 Comparison between two filtering results and true values |
抗差卡尔曼滤波能有效抵抗测量误差对滤波估计值的影响,由图 3可以看出,滤波值在前6期沉降相对稳定时,与真值非常吻合;但在第7、8期快速沉降期间,因抗差估计的影响,滤波模型将真实沉降值当作测量误差,导致该时期滤波值与真值差距较大;第10期之后沉降再次回到相对稳定状态,受运动学模型的影响,二者之间也存在较大的误差。滤波值与真值相差最大时超过13 mm,验后中误差为σ=5.47 mm。

|
图 3 抗差卡尔曼滤波值与测量值及真值的比较 Fig. 3 Comparison of robust Kalman filtering values with measured value and true values |
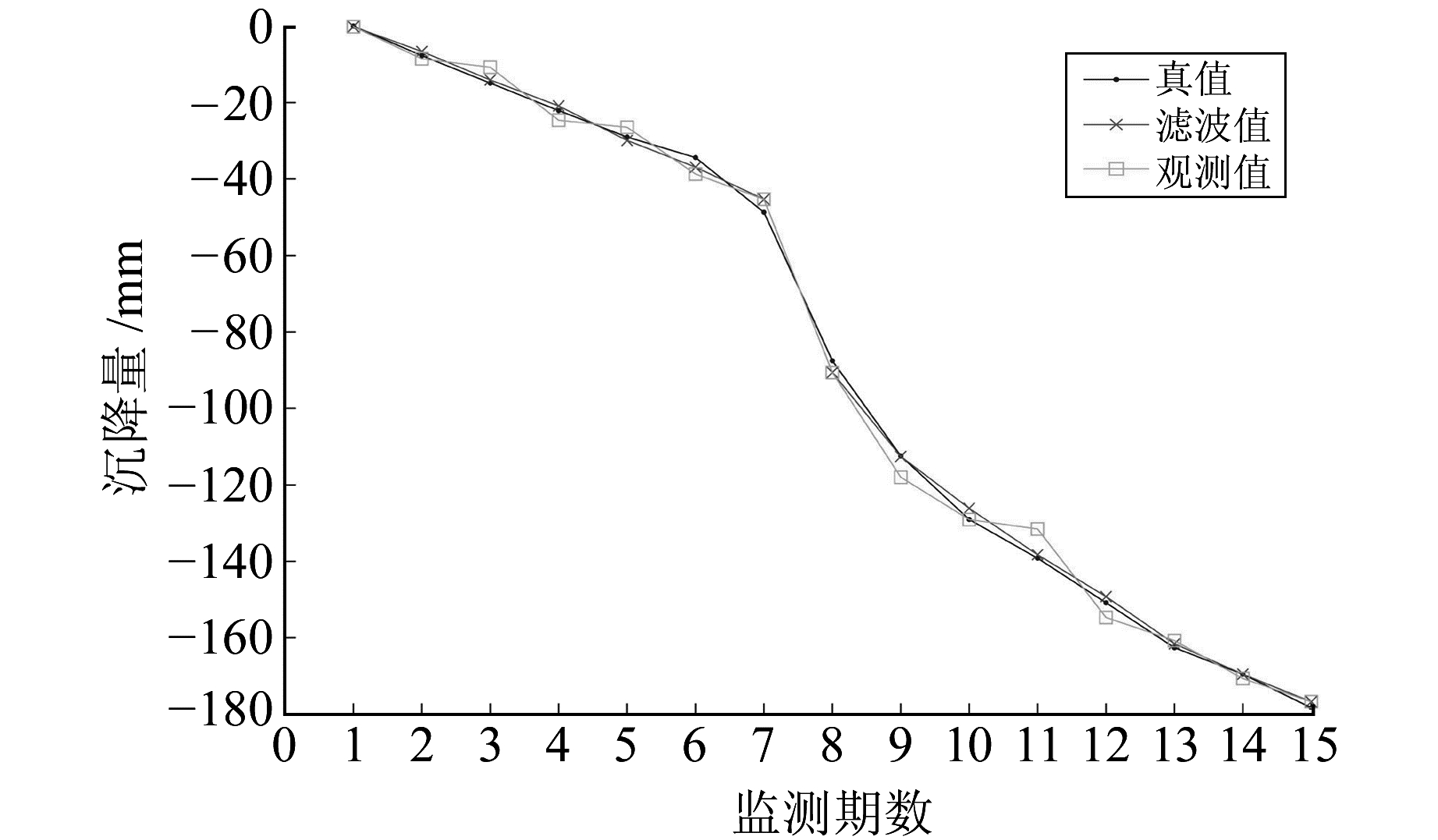
本文设计的抗差自适应卡尔曼滤波不仅能有效抵抗粗差的影响,前6期滤波值贴合真值,第7期快速沉降时也能有效识别出沉降状态的变化,避免抗差估计带来的影响,第10期进入稳定沉降状态时,能够很好地平衡动力学模型预报值与观测值对最终滤波结果的贡献。由图 4可以看出,在稳定沉降期间,以状态模型预报值为主导,控制观测值的影响;在快速沉降期间,加强观测值对滤波结果的影响,有效提高了滤波精度。滤波值与真值相差最大时超过3.5 mm,验后中误差为σ=1.80 mm。
|
图 4 抗差自适应卡尔曼滤波值与测量值及真值的比较 Fig. 4 Comparison of adaptive robust Kalman filtering values with measured values and true values |
塌陷区等地表快速沉降区域如果在快速沉降期间过分依赖有误差的动力学模型,会导致滤波结果出现较大的误差,且在地表快速沉降监测数据的采集过程中,受各种因素的影响,观测值中含有粗差,若单纯使用抗差估计会导致观测值在快速沉降期出现较大的偏差。本文采用的抗差自适应滤波方法不仅能有效识别2种沉降状态,较好地削弱观测异常对滤波的影响,还能较好地抵抗模型带来的误差,得到较为精确的滤波结果。
本文目的在于组建一种抗差自适应滤波方法,对快速沉降区域自动化监测数据进行滤波处理,有效克服观测值的粗差和状态模型对滤波结果的影响。相对于水准测量,该方法能够在较短周期内获得较为准确的沉降信息。另外,单历元观测精度受制于仪器的观测精度,可通过融合多传感器数据以提高每个历元的观测精度。该问题有待进一步研究。
| [1] |
容静, 刘立龙, 康昊华, 等. 基于方差补偿自适应Kalman滤波的ARMA与PSO-SVM模型变形预测[J]. 大地测量与地球动力学, 2018, 38(7): 689-694 (Rong Jing, Liu Lilong, Kang Haohua, et al. The Deformation Prediction of ARMA and PSO-SVM Model Based on Variance Compensation Adaptive Kalman Filter[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 689-694)
(  0) 0) |
| [2] |
Geng Y R, Wang J L. Adaptive Estimation of Multiple Fading Factors in Kalman Filter for Navigation Applications[J]. GPS Solutions, 2008, 12(4): 273-279
(  0) 0) |
| [3] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报:信息科学版, 2003, 28(6): 714-718 (Yang Yuanxi, Xu Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718)
(  0) 0) |
| [4] |
彭月. 一种高效抗差卡尔曼滤波的导航应用[J]. 导航定位学报, 2016, 4(4): 104-107 (Peng Yue. Application of an Efficient Robust Kalman Filtering in Navigation[J]. Journal of Navigation and Positioning, 2016, 4(4): 104-107)
(  0) 0) |
| [5] |
Koch K R, Yang Y. Robust Kalman Filter for Rank Deficient Observation Models[J]. Journal of Geodesy, 1998, 72(7-8): 436-441
(  0) 0) |
| [6] |
Yang Y, He H, Xu G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116
(  0) 0) |
| [7] |
欧吉坤, 柴艳菊, 袁运斌.自适应选权滤波[C].2004年重力学与固体潮学术研讨会暨祝贺许厚泽院士70寿辰研讨会, 武汉, 2004 (Ou Jikun, Chai Yanju, Yuan Yunbin. Adaptive Filtering for Kinematic Positioning by Selection of the Parameter Weights[C]. 2004 Academic Symposium on Gravity and Solid Tide and Symposium on Academician Xu Houze's 70th Birthday, Wuhan, 2004)
(  0) 0) |
| [8] |
张勤, 张菊清, 岳东杰, 等. 近代测量数据处理与应用[M]. 北京: 测绘出版社, 2011 (Zhang Qin, Zhang Juqing, Yue Dongjie, et al. Advanced Theory and Application of Surveying Data[M]. Beijing: Surveying and Mapping Press, 2011)
(  0) 0) |
| [9] |
陈西强, 黄张裕. 抗差估计的选权迭代法分析与比较[J]. 测绘工程, 2010, 19(4): 8-11 (Chen Xiqiang, Huang Zhangyu. Analysis and Comparison of the Selecting Weight Iteration Method in Resistance Robust Estimation[J]. Engineering of Surveying and Mapping, 2010, 19(4): 8-11)
(  0) 0) |
| [10] |
李文文, 傅旭东, 吴文强, 等. 黄河下游水沙突变特征分析[J]. 水力发电学报, 2014, 33(1): 108-113 (Li Wenwen, Fu Xudong, Wu Wenqiang, et al. Study on Runoff and Sediment Process Variation in the Lower Yellow River[J]. Journal of Hydroelectric Engineering, 2014, 33(1): 108-113)
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


