2. 北京市勘察设计研究院有限公司,北京市羊坊店路15号,100038;
3. 济南市勘察测绘研究院,济南市舜华路2000号,250101
高频GNSS可以用来计算地震位移波形[1],也能为地震参数确定、震源过程反演等应用提供一种新的数据源[2-3]。但利用高频GNSS定量确定地震震级精度水平的研究较少。本文基于实测地震的高频GNSS地震波信息快速估计地震震级,并定量评估GNSS地震波测量精度对震级估计的影响。
1 高频GNSS观测及数据处理 1.1 GNSS地震数据2016-11-13新西兰南岛中部地区发生7.8级地震,震中位置为42.53°S、173.05°E,震源深度15 km。此次地震产生多条地表破裂,其中主要破裂从震中开始向北东方向延伸[4-7]。地震发生后不久,新西兰有关机构将地震期间的1 Hz高频GNSS数据发布到互联网上,笔者选取41个GNSS测站数据用于分析研究。站点分布如图 1所示,其中红色五角星为震中的位置,红色矩形为USGS公布的破裂区域。

|
图 1 测站分布 Fig. 1 Distribution map of GNSS stations |
目前,高频GNSS动态定位解算主要有2种方法,即PPP和差分相对定位[8]。差分相对定位方法用于地震地表动态监测时,需要选择一个或多个参考站,而在大地震监测过程中,参考站往往也会受地震影响,从而无法真正准确地获得地震位移波形。而PPP采用单站作业,无需参考站即可获得准确的地震位移波形,因此本文的高频GNSS数据处理采用PPP方法。
利用武汉大学自主研发的PANDA软件进行GNSS定位解算获得地震位移波形[9]。PPP采用IGS提供的精密轨道和CODE提供的5 s钟差产品,利用双频无电离层组合消除电离层延迟误差,采用Saastamoinen模型结合GMF投影函数改正对流层延迟,残余对流层延迟误差采用随机游走估计方式,每2 h估计1次;采用MW组合和LG组合进行周跳探测并且剔除粗差;最后采用滤波或者最小二乘方法进行参数估计,模糊度采用浮点解。为便于分析与比较,将获得的PPP定位时间序列由三维地心坐标(X,Y,Z)转化为当地坐标(E,N,U)。
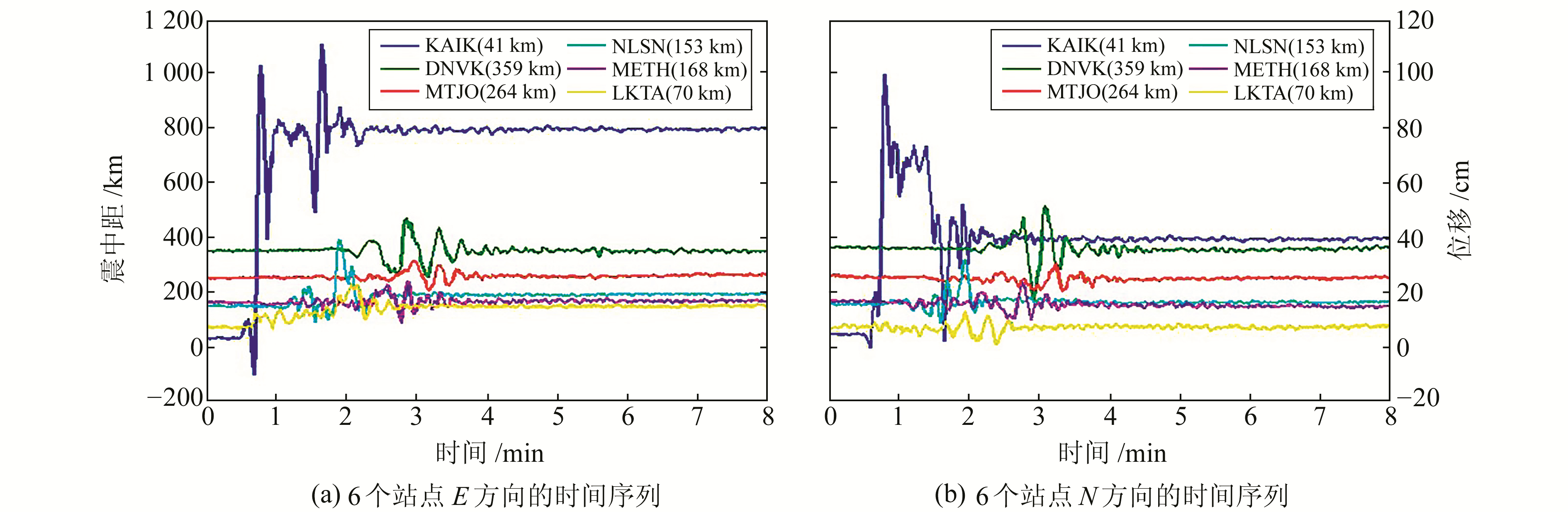
2 地表形变监测分析首先选择6个测站具体分析地震造成的位移变化,分别为震源东北部的DNVK、NLSN、KAIK,震源西南部的MTJO、METH、LKTA。图 2为用GNSS测得的6个测站的水平方向的地震位移波形,其中横轴为时间,零点为GPS时间的发震时刻,左侧纵轴为震中距,右侧纵轴为位移。
|
图 2 GNSS测得的水平方向地震位移波形 Fig. 2 The horizontal displacement waveforms from GNSS stations |
由图 2可见,震源东北部的DNVK站的震源距大于西南部的MTJO站,但是DNVK站水平方向的的位移振幅更大。在震中距相似的情况下,东北部的NLSN站水平方向位移振幅大于西南部的METH站。在震中距较小时,东北部的KAIK站受地震影响较大,出现永久性形变,但西南部的LKTA站形变相对较小。综上,震源东北部的3个测站的瞬时位移比西南部的3个测站都大,这与地震的破裂方向是东北方向的结果相吻合。地震发生时,距离震中较近的KAIK站最先感知到,然后地震波再传到其他各站,震动强度随距离震中的距离及破裂方向的变化而有所变化。该结果也表明高频GNSS可以用于地震地表位移的监测。
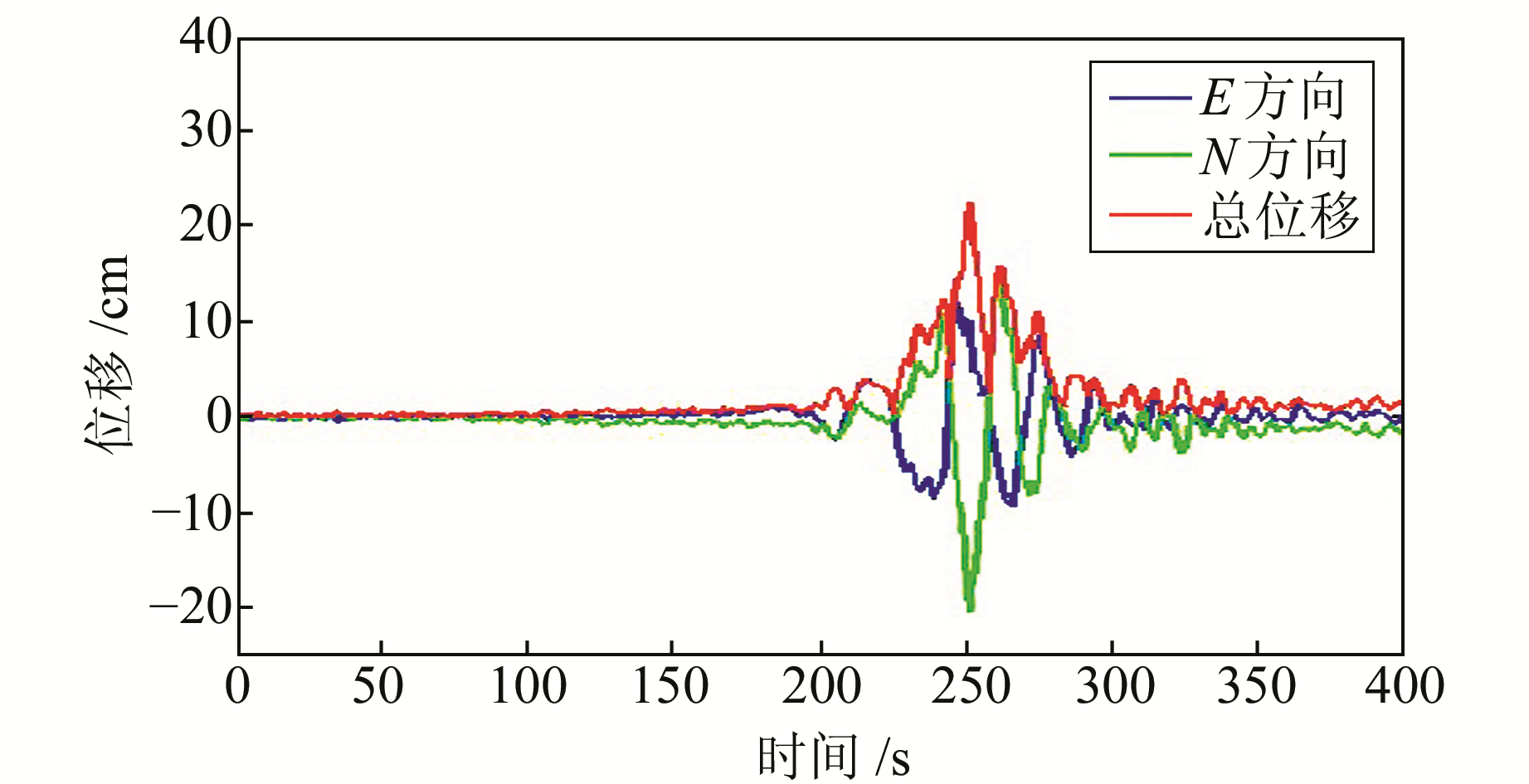
3 峰值地面位移快速确定震级的精度分析 3.1 峰值地面位移的计算根据Gutenberg经验震级公式,为了得到测站的震级,首先需要提取测站水平方向上地震发生前后产生的最大振幅,即峰值地面位移(PGD)。计算方程采用
|
图 3 DNVK站水平方向的地面位移 Fig. 3 Ground displacement in horizontal direction of DNVK station |
一般根据高频GNSS观测到的水平方向最大位移的峰值来确定震级。方荣新等[10]利用3次强震的高频GNSS数据,根据Gutenberg经验震级公式反演强震面波震级:
| $ M=\lg A+1.66 \lg D+2.0 $ |
式中,A为水平方向的峰值地面位移PGD, 计算方法见§3.1,D为震中距,D=arccos(sinBsinB0+cosBcosB0cos(L-L0))R,B和L分别为纬度和经度,B0和L0为震源位置,R为地球平均半径。为快速估计震级,选取初始破裂点进行计算,目的是在地震发生后1~2 min内获取地震的震级信息,为指导抗震救灾提供信息支持。表 1为根据6个测站计算得到的震级结果。
|
|
表 1 利用Gutenberg经验震级公式计算的地震震级 Tab. 1 The magnitudes calculated by the Gutenberg empirical magnitude formula |
由表 1可以看出,震源东北方向的测站计算的震级比震源西南方向的大,说明在地震传播方向上估计的震级较大。为了削弱地震传播方向、测站地质构造条件、观测墩稳定性等因素的影响,可以尽量采用更多可用的测站数据。因此,本研究计算所有41个测站的震级,取平均以获得更准确的结果。
如图 4,所有测站计算的震级分布在6.65~8.7之间,平均值为7.87,在震中距小于100 km时,测站震级小于7.87级;在震中距大于650 km时,测站震级大于7.87级。其原因可能为,当震中距太小时不能把震源看作点源,计算震级容易出现误差;地震波在传播过程中,地球介质会使高频地震波信号逐渐衰减,当震中距太大时,地震波主要表现为低频部分,而低频能量所引起的地表震动位移与高频能量引起的位移不成比例关系。因此,震中距和峰值地面位移的比例关系也会发生变化,最终震级计算经验公式可能不完全适用,所以本文的计算公式有一定的适用范围。另外,测站周围的地质构造条件如岩石土壤等有所差异,测站观测墩高度也不尽相同,由此计算的震级与实际震级会有一定的偏差。

|
图 4 高频GNSS反演的地震震级值 Fig. 4 Earthquake magnitude values of high frequency GNSS inversion |
高频GNSS定位观测会受到钟差、测量噪声、多路径等多种误差的影响,而这些误差在数据处理过程中并不能完全消除。通过PANDA软件PPP模块计算的结果在高程方向精度约为3~5 cm,水平方向精度约为1~2 cm。在计算震级时,这些误差会使PGD很难精确确定,从而对计算出的震级造成一定的误差,由此,本文进一步探讨PGD的精度对震级估计的影响。
3.3 峰值地面位移精度对震级的影响在Gutenberg经验震级公式中,影响震级的变量为震中距和峰值地面位移,本文着重探讨PGD测量精度对震级的影响。首先假设求解的PGD是正确的,则对每个测站的峰值振幅分别改变相同幅度后,会对震级的大小产生一定的影响。
如图 5,从上到下为每个测站的PGD依次改变固定值+3 cm、+2 cm、+1 cm、0 cm、-1 cm、-2 cm、-3 cm后的平均震级,红线表示振幅未改变时的震级(7.87级)。表 2为PGD改变对平均震级的影响,即当每个测站PGD依次改变+3 cm、+2 cm、+1 cm、0 cm、-1 cm、-2 cm、-3 cm时,平均震级值依次为7.97、7.94、7.91、7.87、7.82、7.77、7.70。可以看出,改变后的平均震级随着PGD的增加而增大,并且当PGD的变化范围在-2~ 2 cm时,对平均震级的影响小于等于0.1。

|
图 5 振幅精度(增加固定误差)对震级的影响 Fig. 5 Influence of amplitude precision (increasing the fixed error) on magnitude |
|
|
表 2 振幅精度(增加固定误差)对平均震级的影响 Tab. 2 Influence of amplitude precision(increasing the fixed error) on measured average magnitude |
假设所有测站的PGD误差同时达到最小值-d1或最大值d2(d1、d2均为正值),则对应的平均震级分别为M1和M2。如果所有测站的PGD误差随机地落在-d1~d2范围内,得到的平均震级区间一定在M1~M2内。因此,通过控制每个测站PGD的误差范围,可以有效控制平均震级的范围,防止出现较大的震级估计误差。以本文所分析的地震为例,根据上述计算结果可知,若能把每个测站的PGD误差控制在-2 ~ 2 cm范围内,则对平均震级的影响也会在7.77~7.97范围内,震级误差小于等于0.1。即当每个站的PGD精度控制在2 cm范围时,对平均震级的影响在0.1以内。
基于此,用下面的模拟实验进行验证。如图 6所示,从上到下为对每个测站的PGD依次增加不同范围的随机误差后所得到的平均震级,随机误差的范围从上到下依次为+2~+3 cm、+1~+2 cm、0~+1 cm、0 cm、0~-1 cm、-1~-2 cm、-2~-3 cm,红线表示振幅未改变时的震级(7.87级)。表 3为PGD增加随机误差后对平均震级的影响,可以看出,改变后的平均震级随着PGD的增加而增大,与表 2增加固定值所得到的结果相似。尤其是当对每个测站增加的随机误差在-2~ +2 cm范围时,该随机实验得到的结果差值为0.01。

|
图 6 振幅精度(增加随机误差)对震级的影响 Fig. 6 Influence of amplitude precision(increasing the random error) on magnitude |
|
|
表 3 振幅精度(增加随机误差)对平均震级的影响 Tab. 3 Influence of amplitude precision(increasing the random error) on measured average magnitude |
此外,PGD对震级的影响会随着震中距的变化而变化。每隔100 km选取一个测站,从表 4可知,当每个测站的PGD改变同样的大小时,随着测站震中距逐渐增大,震级的差值也大致呈增大趋势,说明震中距越大,估计的震级对PDG越敏感。例如,当测站距离震源50 km左右时,PGD的精度对震级的计算影响不大;在距离震中150~450 km时,PGD精度在4 cm以内时,对震级计算的影响在0.1以内;当震中距大于550 km时,PGD精度在4 cm时,对震级计算的影响已经远大于0.1,PGD精度对震级影响较大。
|
|
表 4 不同震中距的测站PGD精度对测站震级的影响 Tab. 4 Influence of PGD accuracy of stations with different epicentral distances on station magnitude |
本文利用高频GNSS测得的PGD进行快速确定震级的精度分析,通过PANDA软件的精密单点定位模块获得2016-11-13新西兰地震当天站点的动态位移,然后由精密单点定位的结果展开一系列的分析。结果表明:
1) 高频GNSS观测能够准确记录地震时地表产生的形变,可以用来观测地震的动态位移变化。横轴的时间可以准确记录地震发生的时间,结合震源周围各站点的位置变化量可以预测地震破裂及传播的方向、地表变形程度。震动强度随与震中的距离及破裂方向而变化,且在传播方向上距离越近感受到的震动越明显。
2) 在震级计算时,测站周围的地质构造条件如岩石土壤等有所差异,测站观测墩高度也不尽相同,因此计算的震级与实际震级会有一定的偏差。对于该地震而言,当每个站的PGD精度控制在2 cm范围内时,对平均震级的影响会在0.1以内。PGD会随着震中距的增加而逐渐衰减,震中距较大时测站PGD更不容易准确测得,但是此时PGD精度对震级的影响最大。因此采用PGD方法估计震级时,出于时效性和准确性的考虑,建议尽量避免采用震中距超远的测站。
| [1] |
Shi C H, Lou Y D, Zhang H, et al. Seismic Deformation of the MW8.0 Wenchuan Earthquake from High-Rate GPS Observations[J]. Advances in Space Research, 2010, 46(2): 228-235 DOI:10.1016/j.asr.2010.03.006
(  0) 0) |
| [2] |
Fang R X, Shi C, Song W W, et al. Determination of Earthquake Magnitude Using GPS Displacement Waveforms from Real-Time Precise Point Positioning[J]. Geophysical Journal International, 2014, 196(1): 461-472 DOI:10.1093/gji/ggt378
(  0) 0) |
| [3] |
Melgar D B, Crowell W, Geng J H, et al. Earthquake Magnitude Calculation without Saturation from the Scaling of Peak Ground Displacement[J]. Geophyscial Research Letters, 2015, 42(13): 5 197-5 205 DOI:10.1002/2015GL064278
(  0) 0) |
| [4] |
Cesca S, Zhang Y, Mouslopoulou V, et al. Complex Rupture Process of the MW7.8, 2016, Kaikoura Earthquake, New Zealand, and Its Aftershock Sequence[J]. Earth and Planetary Science Letters, 2017, 478: 110-120 DOI:10.1016/j.epsl.2017.08.024
(  0) 0) |
| [5] |
Litchfield N J, Villamor P, Dissen R J, et al. Surface Rupture of Multiple Crustal Faults in the 2016 MW7.8 Kaikoura, New Zealand, Earthquake[J]. Bulletin of the Seismological Society of America, 2018, 108(3B): 1 496-1 520 DOI:10.1785/0120170300
(  0) 0) |
| [6] |
Zhang H, Koper K D, Pankow K, et al. Imaging the 2016 MW7.8 Kaikoura, New Zealand, Earthquake with Teleseismic P Waves: A Cascading Rupture across Multiple Faults[J]. Geophysical Research Letters, 2017, 44(10): 4 790-4 798 DOI:10.1002/2017GL073461
(  0) 0) |
| [7] |
韩竹军, Litchfield N, 冉洪流, 等. 新西兰2016年凯库拉MW7.8地震地表破裂带特征初析[J]. 地震地质, 2017, 39(4): 55-68 (Han Zhujun, Litchfield N, Ran Hongliu, et al. Primarily Study on Features of Surface Ruptures Induced by the 2016 MW7.8 Karkoure Earthquake, New Zealand[J]. Seismology and Geology, 2017, 39(4): 55-68)
(  0) 0) |
| [8] |
范士杰, 刘焱雄, 张健. PPP与GAMIT/TRACK在地震监测中的应用[J]. 测绘科学, 2013, 38(2): 184-186 (Fan Shijie, Liu Yanxiong, Zhang Jian. Application PPP of and GAMIT /TRACK Module in Earthquake Monitoring[J]. Science of Surveying and Mapping, 2013, 38(2): 184-186)
(  0) 0) |
| [9] |
陈克杰, 方荣新, 李敏, 等. PANDA软件在高频数据PPP动态定位中的应用研究[J]. 大地测量与地球动力学, 2011, 31(4): 132-134 (Chen Kejie, Fang Rongxin, Li Min, et al. Research on Application of PANDA Software to High Frequency Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 132-134)
(  0) 0) |
| [10] |
方荣新, 施闯, 王广兴, 等. 利用高频GPS确定大地震震中和震级研究:2008年汶川8.0级地震应用结果[J]. 中国科学D辑:地球科学, 2014, 44(1): 90-97 (Fang Rongxin, Shi Chuang, Wang Guangxing, et al. Epicenter and Magnitude of Large Earthquake Determined from High-Rate GPS Observations: A Case Study of the 2008 M8.0 Wenchuan Earthquake[J]. Science China Series D: Earth Sciences, 2014, 44(1): 90-97)
(  0) 0) |
2. Beijing Engineering Consultants Co Ltd, 15 Yangfangdian Road, Beijing 100038, China;
3. Ji'nan Institute of Surveying and Mapping, 2000 Shunhua Road, Ji'nan 250101, China
 2019, Vol. 39
2019, Vol. 39

