2. 中国地震局地震工程与工程振动重点实验室,哈尔滨市学府路29号,150080;
3. 福建省地震局,福州市华鸿路7号,350003
气枪震源由于具有可靠性和信号可重复性高及宽频带等优点,在海上地震勘探中逐渐成为主流。近几年扩展到内陆水域,通过陆域激发实验进行深部构造探测的尝试[1-4]。传统的通过在实际工作和实验中获取震源子波参数的方式需耗费大量的人力和物力,而通过气枪子波的理论可以对不同激发和接收条件下单枪及枪阵的效果进行模拟,提高效率,减少实验成本[5]。
对于气枪震源子波的模拟,Ziolkowski等[6-7]最早提出气泡振荡的物理模型,给出著名的近场声波压力场计算方法,并通过近场观测将单枪理论进一步发展到枪阵理论。Landrø等[8]在Ziolkowski模型基础上加入新的衰减项,并提出一个线性关系式来表示气室内气体的释放;Langhammer等[9-10]将温度和粘度因素考虑进模型中;Laws等[11]引入气泡内部蒸发冷凝导致物质交换、经典热扩散、枪口节流等修正因素;Li等[12]和Wang等[13]将气泡上升、表面反射等因素加入模型,经过多因素修正,模拟结果得到进一步改善。
为增强震源能量,提高子波品质,常规海上勘探一直以压制气泡脉冲为重点,其中最常用的方式是协调阵列组合和相干阵列组合。但对于陆域深部地壳及地幔的探测,宽频带的地震资料采集要求震源信号具有更好的穿透性,这就要求在实际激发时,尽量避免气枪之间相干作用引起的气泡振荡抑制,使子波低频能量不被减弱。本文针对深部探测适用性更好的大容量单枪与非相干枪阵的子波模拟模型进行实验与改进,并对影响模拟效果的各种重要因素进行讨论。
1 实验数据获取与模型优化原理 1.1 实验数据获取2018-07福建省地震局在总库容为5 251万m3的泉州市龙门滩水库开展相关实验,其地理位置及周边环境见图 1。实验选取了4支单枪容量2 000 in3的1500 LL型Bolt枪组成气枪阵列,进行单枪和枪阵实验,气枪摆放于8 m×6 m浮台四角处,保证枪阵激发实验时气泡之间相互独立、互不影响。水听器置于浮台周边不同距离处,用来记录水中传播的压力波。

|
图 1 实验现场 Fig. 1 Experiment site |
Gilmore方程[14]是最常用于描述水下爆炸气泡动力学的方程,包含了由于声能辐射和压力传播导致气泡能量衰减的一个二阶可压缩衰减项,是Ziolkowski模型的基础,其形式为:
| $ \begin{array}{l} \ddot R = \\ \frac{{H\left( {1 + \frac{{\dot R}}{c}} \right) + \left( {1 - \frac{{\dot R}}{c}} \right)\frac{R}{{c\dot H}} - \frac{3}{2}{{\dot R}^2}\left( {1 - \frac{{\dot R}}{{3c}}} \right)}}{{R\left( {1 - \frac{R}{c}} \right)}} \end{array} $ | (1) |
式中,H为焓差,R为气泡半径,c为所在位置声速。基于上述振荡方程,Ziolkowski[6]推得压力子波方程与速度方程为:
| $ P - {P_\infty } = \rho \left( {\frac{y}{r} - \frac{{{u^2}}}{2}} \right) + \frac{\rho }{{2{c_\infty }}}{\left( {\frac{y}{r} - \frac{{{u^2}}}{2}} \right)^2} $ | (2) |
| $ u = \frac{y}{{{c_\infty }r}} + \frac{{K{y^2}}}{{c_\infty ^3{r^2}}}\left( {1 - \frac{y}{{c_\infty ^2r}} + \frac{{{K^2}{y^4}}}{{2{c_\infty }8{r^4}}}} \right) $ | (3) |
| $ K = \frac{{c_\infty ^3{R^2}v}}{{{y^2}}}\left( {1 - \frac{{{v^2}}}{{2c_\infty ^2}}} \right) - \frac{{c_\infty ^2R}}{y}\left( {1 - \frac{v}{{{c_\infty }}}} \right) $ | (4) |
| $ y = R\left( {H + \frac{{{v^2}}}{2}} \right) $ | (5) |
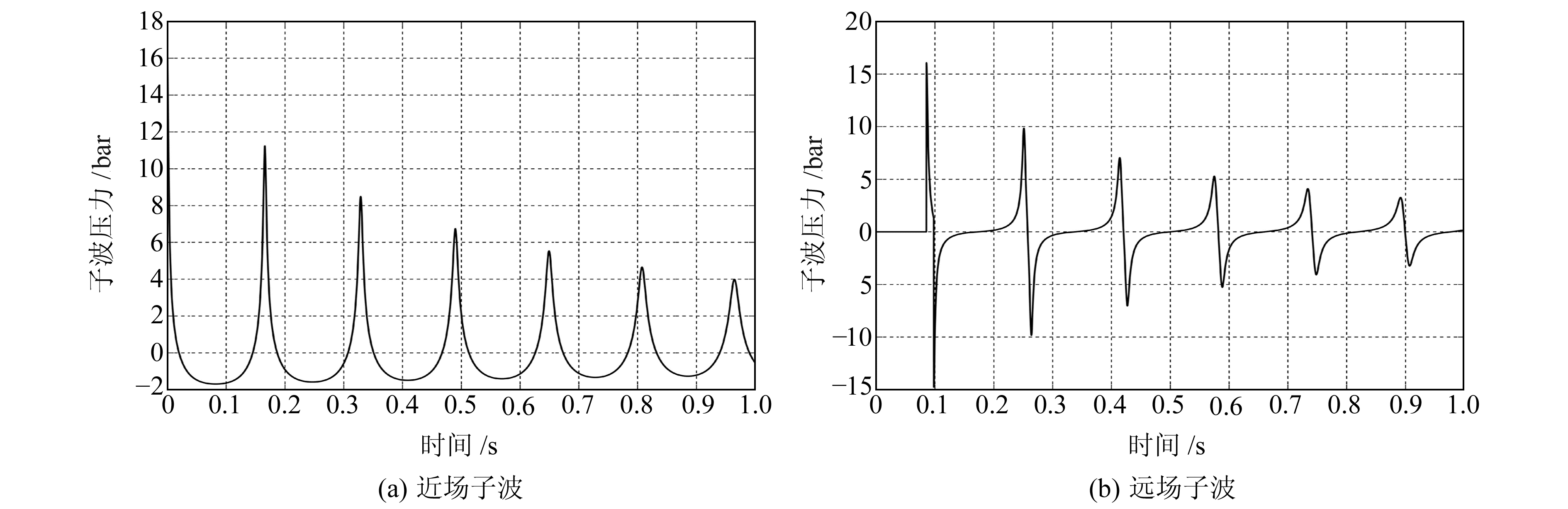
式中,P∞为无穷远处压力,ρ为水密度,v为气泡壁振荡速度,c∞为水中声波速度。具体激发参数为:气枪枪压2 000 psi,容量2 000 in3,沉放深度9 m,近场检波器检波距离1 m,远场125 m,水中波速取实测值1 446 m/s,虚反射系数-1。利用经典的变步长四阶龙格库塔算法,可得到未经优化的Ziolkowski模型近远场压力子波波形,结果见图 2。
|
图 2 近远场压力子波波形 Fig. 2 Waveform of pressure wavelet of near and far field |
由图 2可知,Ziolkowski模型作为一个简化模型具有许多不足之处,如气体瞬间全部释放、球形的假设与实际不符、没有考虑枪体的存在及气泡与水之间的热量交换等,导致预测的振荡结果衰减慢、持续时间长、主脉冲幅值过大,而实际的子波记录显示,典型的气枪气泡在前几次的振荡后就会消耗殆尽。基于此,本文引入一些重要的附加影响因素对原有模型进行改进。
为对气枪击发初始释放阶段气枪与气泡的物质和能量交换进行刻画,根据Landrø等[8]的研究,引入开放式热力学系统:
| $ h \frac{\mathrm{d} m}{\mathrm{d} t}+\frac{\mathrm{d} Q}{\mathrm{d} t}=\frac{\mathrm{d} U}{\mathrm{d} t}+P \frac{\mathrm{d} V}{\mathrm{dt}} $ | (6) |
式中,h=CpTg为进入系统的气体的焓,其中Tg为气枪内温度,Cp为等压比热容,取29.05 J/(mol ·K),dQ为吸收的热量,U为气泡气体的内能,U=mCvTb,其中Tb为气泡内气体温度,Cv为等容比热容,取20.75 J/(mol ·K),最后一项为对外做的功。由式(6)可得:
| $ \frac{{{\rm{d}}{T_b}}}{{{\rm{d}}t}} = \frac{{\left( {{C_p}{T_k} - {C_v}{T_b}} \right)\frac{{{\rm{d}}m}}{{{\rm{d}}t}} + \frac{{{\rm{d}}Q}}{{{\rm{d}}t}} - P\frac{{{\rm{d}}V}}{{{\rm{d}}t}}}}{{m{C_v}}} $ | (7) |
其中,
| $ \begin{array}{l} \frac{{{\rm{d}}m}}{{{\rm{d}}t}} = \\ \left\{ {\begin{array}{*{20}{l}} {\sqrt {\frac{{{P_g}{m_g}2\gamma \left[ {{{\left( {\frac{P}{{{P_g}}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}} - 1} \right]{{\left( {\frac{P}{{{P_g}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}}}{{{v_g}}}} ,m > \eta {m_g}|{t_{ = 0}}}\\ {0,m \le \eta {m_g}|{t_{ = 0}}} \end{array}} \right. \end{array} $ | (8) |
式中,mg为气枪气室气体质量,vg为气室体积,Pg为工作压力,P为气泡内压,γ为绝热常数,取1.13,A为枪口截面积,η为气体的释放率,即气枪排出气体的质量与气枪初始状态气枪质量之比,随着枪体老化,该系数会变小,本文取0.75。
根据Laws等[11]的研究,气泡内外的热传导可近似为一维稳态导热,气泡内温度均匀分布,并且由于气泡表面的湍流,温度梯度仅存在于一个边界薄层内,其厚度公式为:
| $ {d = 4D{{{\mathop{\rm Re}\nolimits} }^{\frac{{ - 3}}{4}}}{{\Pr }^{\frac{{ - 1}}{2}}}} $ | (9) |
| $ {{\mathop{\rm Re}\nolimits} = \frac{{\rho uR}}{\mu }} $ | (10) |
式中,D为气泡直径,Re为雷诺数,Pr为普朗特常数,u为振荡速度,μ为水的粘滞系数。通过边界层的热传导率为:
| $ \dot{Q}=\Delta T A \frac{k}{d} $ | (11) |
式中,A为气泡的表面积,ΔT为气泡壁内外温度差,k/d取4 000 W/(m2K)[18]。
除了传导的热交换,Ziolkowski等[7]提出气泡壁蒸发冷凝产生的潜热吸收和释放不容忽视。对于水气的质量转换速率,Fuijkawa等[17]给出:
| $ \dot{m}_{v}=4 \pi R^{2} \frac{\alpha_{M}}{\sqrt{2 \pi R_{G}}}\left[\frac{P_{V}^{*}}{\sqrt{T_{W}}}-\Gamma \frac{P_{V}}{\sqrt{T}}\right] $ | (12) |
式中,TW、PV*为气泡所处流体环境下的温度和饱和蒸气压力,T、PV为气泡内部温度及对应饱和蒸气压,αM与Γ为经验系数,分别为0.04和1。潜热的交换速率为:
| $ \dot{Q}=\dot{m}_{V} L $ | (13) |
式中,L为蒸发潜热,取2.45 J/kg。对于大容量的气枪震源,另一个重要的压力子波影响因素就是气枪自身体积对气泡的影响,对于此项的校正可采用下式:
| $ V=\frac{4}{3} \pi R^{3}-V_{0} $ | (14) |
式中,V0为气枪体积,取0.065 m3,R为气泡半径。
由于气泡表面湍流会产生涡旋,导致气泡表面变粗糙,水气作用接触面增大,意味着能量衰减更快。Laws等[11]引入有效粘度作为进一步气泡振荡能量的耗散,有效粘滞系数公式为:
| $ u_{\mathrm{eff}}=\mu(1+K \mathrm{Re}) $ | (15) |
式中,μ为正常状态下水的粘滞系数,K为常数,取0.02,雷诺数可由Re=ρuR/μ计算,R为气泡半径,ρ为水的密度,u为气泡振荡速度。
2 影响要素分析以及模拟结果与观测子波的对比 2.1 各因素对模拟结果产生的影响分析通过引入校正因素,将校正后的模型分别与原始模型进行对比,结果见图 3(a)和3(b)。对各影响因素进行归一化计算,分析各影响因素的优先性,结果见图 3(c)。

|
图 3 校正后的模型模拟结果与原始模型的对比 Fig. 3 Comparison of the corrected model simulation results with the original model |
由图 3(a)和3(c)可知,有效粘度对于子波的衰减影响较小,与Langhammer等[9]的水箱内微型气枪激发实验结果相吻合。由于蒸发冷凝导致水气转换引起的波形变化相较而言非常明显,波形振幅幅值显著减小,但其对气泡半径及振荡周期的影响较弱。而位于气泡中心的枪体会使实际气体体积比气泡体积要小,导致子波振幅显著增大,对于此次实验中所用的大容量气枪尤为明显。同时,枪体的存在还会导致气泡半径的增加及振荡速度和振荡周期的减小。
由图 3(b)和3(c)可知,枪口节流明显降低了压力脉冲幅值,限制初始气泡的最大半径、气泡内外的压力差及振荡子波的振幅强度,周期也会减小。对于热传导,其对应子波振幅衰减速度明显加快,气泡半径、振荡速度都有所减小,初泡比和振荡周期增加。通过考虑气体释放因素前后所得压力子波曲线的对比可知,气体的释放率对于气泡周期的改造尤为明显。综合各种因素后可以发现,水气转换、枪口节流、热传导等因素使模拟结果的压力子波衰减更快,与实际更相符,尤其是枪体的存在及热传导,进一步优化了压力脉冲,而释放率及枪口节流的主要作用是改进气泡周期预测。综上所述,各种因素改进使得气泡振荡周期及振幅衰减加快,初始压力子波得到压制却校正过量,但改进的模型整体与实际子波更相近。
2.2 模拟结果与观测子波的对比本文所用实际波形数据采用同样工况条件下多次重复观测来剔除异常记录,并通过取平均值来减小误差。对于单枪记录,分别选取距离震源1 m、30 m、80 m、125 m的水听器,用以验证改进的单枪模型的适用性。多枪枪阵远场子波是地震研究关心的重点,但因为水域条件限制仅选取距离震源125 m处的子波记录作为代表,与模拟结果进行对比。另外,由于各枪之间相互影响很小,远场子波模拟可由优化的单枪线性叠加确定。假设第i支气枪在第j个观测点处子波为Pij(t),满足:
| $ {P_j}(t) = \sum\limits_{i = 1}^n {\frac{{{P_i}\left( {t - {r_{ij}}/c} \right)}}{{{r_{ij}}}}} $ | (16) |
式中,c为声速,t为时间,rij为第i支枪到j处水听器的距离。根据经验,当枪阵总容量一定时,小容量多枪阵列能量输出是大容量单枪的n2/3倍[18](n为气枪数量),可以以此作为模拟枪阵子波的校正。
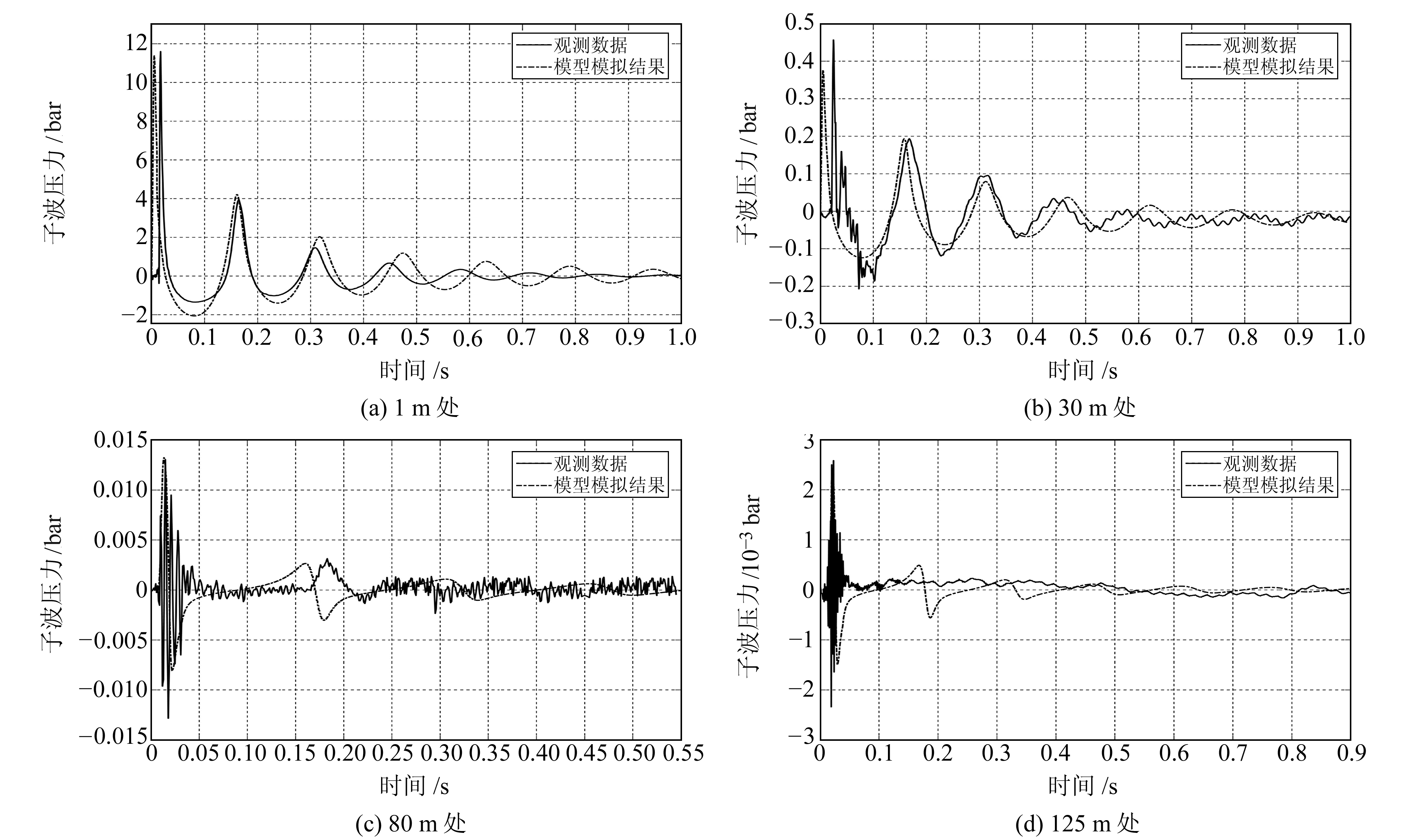
单枪不同距离处记录子波与模拟的对比结果见图 4。由图 2和4可知,考虑多种附加因素可使原始模型的初始压力脉冲幅值显著减小,模拟值与实测值更加接近。对于近场而言,预测值甚至低于实测值,结合图 3(c)分析认为,这可能是由于热传导的修正不足及气枪各自独特的喷气出口节流作用的复杂性导致的。随着距离的增大,水体等因素对实际记录子波的影响迅速衰减,观测值与预测值的压力脉冲值匹配度较高。根据距离较近的2个子波记录(图 4(a)和4(b))结果显示,随着时间的推移,气泡振荡压力的模拟曲线与实际相比误差开始增大,尤其是第3个周期之后。结合Graaf等[19]的研究结果认为,振荡随时间推移变得越来越混乱和无序,以致气泡球形不再明显,同时气团的湍流使得气团表层物质及能量的交换更加剧烈和复杂,球形假设模型误差越来越大。图 4(c)和4(d)显示,随着距离变远,实测波形锯齿现象严重,80 m处仅能识别到一个非常明显的气泡脉冲,125 m处已无法识别到气泡脉冲,说明水库复杂的水体及周边环境对波形的强烈改造作用,使得相对较弱的单枪气泡脉冲无法被识别,对比结果也不大理想。
|
图 4 不同距离处单枪子波模拟结果与实测结果的对比 Fig. 4 Comparison of the measured signatures at differ distance away from the seismic source with the improved model |
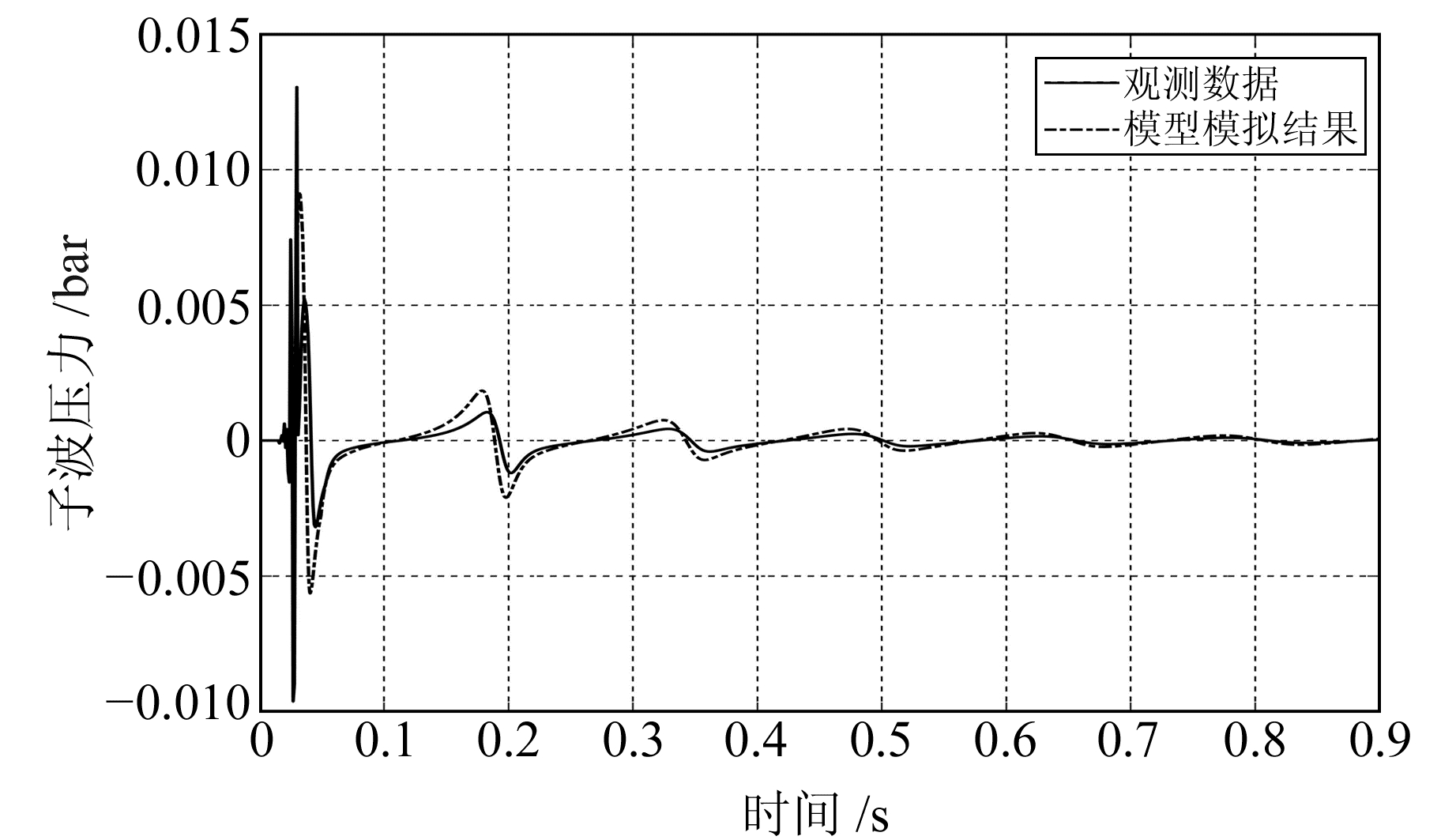
图 5为利用枪阵形式激发得到的远场子波记录与模拟结果的对比,参考单枪对比记录可以发现,枪阵的模拟效果明显优于单枪。枪阵由于能量得到提高,水听器能记录到明显的主脉冲和多个气泡脉冲,波形的振幅均得到增加,其中气泡脉冲增加幅度大于主脉冲振幅,记录的波形锯齿现象也得到改善。采用这种非相干枪枪阵排列方法可以明显加强低频能量,增加有效频带宽度,对于陆域的深部探测更加有效。实验发现,由于水深及水库边界的影响,相较于海上实验,环境较差的陆域水库,尤其是小水体,激发时气枪子波在较近的距离(50 m左右)就展现出远场特性。利用多因素改进的模型与陈浩林等[20]选用经验气泡半径衰减因子进行修正的方法相比,展现的实际物理意义更加丰富,可以大致分析及解释误差来源,进一步理解气枪击发产生的子波,不单一追求修正压力子波与观测子波波形上的相近。
|
图 5 远场枪阵子波模拟结果与实测结果的对比 Fig. 5 Comparison of the measured signatures at far field with the improved model |
本文引入多种重要的能量耗散因子对经典的气枪震源子波模型进行改进,分析各引入因子的影响发现,由于气泡壁的湍流导致的热传导是气泡模型改进的关键。通过与实测压力子波对比发现,改进的模型与原始模型相比,在子波波形的预测能力上得到很大改善。在实际枪阵设计中,综合考虑激发能量、振幅谱特性、初泡比、关枪分析等是非常必要的,而改进的气枪子波模型能够获取更准确的特征。对各种气枪的排布组合效果进行模拟评估,为枪阵的设计减少实际测试工作,模拟得到的远场子波也将进一步用于优化地震资料的处理。然而,子波波形的对比也显示,模拟结果与观测结果之间仍然存在一定误差,其原因可能是假设条件与实际不符(数个振荡后的非球形与模型的球形假设等)。另外,陆域水体复杂的水体环境尤其是边界的反射,是影响激发及模拟效果的重要因素,本文未对此进行探讨,下一步将针对陆域半无界界面的影响展开研究。
| [1] |
丘学林, 陈顒, 朱日祥, 等. 大容量气枪震源在海陆联测中的应用:南海北部试验结果分析[J]. 科学通报, 2007, 52(4): 463-469 (Qiu Xuelin, Chen Yong, Zhu Rixiang, et al. Application of Large-Capacity Airguns Source in Sea-Land Joint Measurement: Analysis of Experimental Results in the Northern Area of the South China Sea[J]. Chinese Science Bulletin, 2007, 52(4): 463-469 DOI:10.3321/j.issn:0023-074X.2007.04.015)
(  0) 0) |
| [2] |
林建民, 王宝善, 葛洪魁, 等. 大容量气枪震源特征及地震波传播的震相分析[J]. 地球物理学报, 2008, 51(1): 206-212 (Lin Jianmin, Wang Baoshan, Ge Hongkui, et al. Study on Large Volume Airgun Source Characteristics and Seismic Phase Analysis[J]. Chinese Journal of Geophysics, 2008, 51(1): 206-212 DOI:10.3321/j.issn:0001-5733.2008.01.025)
(  0) 0) |
| [3] |
陈浩林, 全海燕, 於国平, 等. 气枪震源理论与技术综述(上)[J]. 物探装备, 2008, 18(4): 211-217 (Chen Haolin, Quan Haiyan, Yu Guoping, et al. Summary of Airgun Source Theory and Technology(1)[J]. Equipment for Geophysical Prospecting, 2008, 18(4): 211-217 DOI:10.3969/j.issn.1671-0657.2008.04.001)
(  0) 0) |
| [4] |
陈浩林, 全海燕, 於国平, 等. 气枪震源理论与技术综述(下)[J]. 物探装备, 2008, 18(5): 300-308 (Chen Haolin, Quan Haiyan, Yu Guoping, et al. Summary of Airgun Source Theory and Technology(2)[J]. Equipment for Geophysical Prospecting, 2008, 18(5): 300-308 DOI:10.3969/j.issn.1671-0657.2008.05.004)
(  0) 0) |
| [5] |
李绪宣, 温书亮, 顾汉明, 等. 海上气枪阵列震源子波数值模拟研究[J]. 中国海上油气, 2009, 21(4): 215-220 (Li Xuxuan, Wen Shuliang, Gu Hanming, et al. A Numerical Simulation of Wavelets from Offshore Air-Gun Array Seismic Source[J]. China Offshore Oil and Gas, 2009, 21(4): 215-220 DOI:10.3969/j.issn.1673-1506.2009.04.001)
(  0) 0) |
| [6] |
Ziolkowski A. A Method for Calculating the Output Pressure Waveform from an Air Gun[J]. Geophysical Journal International, 1970, 21(2): 137-161 DOI:10.1111/j.1365-246X.1970.tb01773.x
(  0) 0) |
| [7] |
Ziolkowski A, Parkes G, Hatton L, et al. The Signature of an Air Gun Array: Computation from Near-Field Measurements Including Interactions[J]. Geophysics, 1982, 47(10): 1 413-1 421 DOI:10.1190/1.1441289
(  0) 0) |
| [8] |
Landrø M, Sollie R. Source Signature Determination by Inversion[J]. Geophysics, 1992, 57(12): 1 633-1 640 DOI:10.1190/1.1443230
(  0) 0) |
| [9] |
Langhammer J, Landrø M. Experimental Study of Viscosity Effects on Air-Gun Signatures[J]. Geophysics, 1993, 58(12): 1 801-1 808 DOI:10.1190/1.1443395
(  0) 0) |
| [10] |
Langhammer J, Landrø M. Temperature Efforts on Airgun Signatures[J]. Geophysical Prospecting, 1993, 41(6): 737-750 DOI:10.1111/j.1365-2478.1993.tb00881.x
(  0) 0) |
| [11] |
Laws R M, Hatton L, Haartsen M. Computer Modelling of Clustered Airguns[J]. First Break, 1990, 8(9): 331-338
(  0) 0) |
| [12] |
Li G F, Cao M Q, Chen H L, et al. Modeling Air Gun Signatures in Marine Seismic Exploration Considering Multiple Physical Factors[J]. Applied Geophysics, 2010, 7(2): 158-165 DOI:10.1007/s11770-010-0240-y
(  0) 0) |
| [13] |
Wang F F, Liu H S. Simulating the Signature Produced by a Single Airgun under Real Gas Conditions[J]. Applied Geophysics, 2014, 11(1): 80-88 DOI:10.1007/s11770-014-0408-6
(  0) 0) |
| [14] |
Gilmore F R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid[EB/OL]. https://authors.library.caltech.edu/561/, 2005
(  0) 0) |
| [15] |
Liu Y, Ni C Z, Chen H L, et al. Parameter Optimization in Air-Gun Type-Dependent Signature Modelling[C]. 73rd EAGE Conference and Exhibition Incorporating SPE EUROPEC, Vienna, 2011
(  0) 0) |
| [16] |
Cook J A, Gleeson A M, Roberts R M, et al. A Spark-Generated Bubble Model with Semi-Empirical Mass Transport[J]. The Journal of the Acoustical Society of America, 1997, 101(4): 1 908-1 920 DOI:10.1121/1.418236
(  0) 0) |
| [17] |
Fujikawa S, Akamatsu T. Effects of the Non-Equilibrium Condensation of Vapour on the Pressure Wave Produced by the Collapse of a Bubble in Liquid[J]. Journal of Fluid Mechanics, 1980, 97(3): 481-512 DOI:10.1017/S0022112080002662
(  0) 0) |
| [18] |
夏季, 金星, 蔡慧腾, 等. 大容量气枪阵列子波时频特性及其影响因素[J]. 地震研究, 2017, 40(1): 111-121 (Xia Ji, Jin Xing, Cai Huiteng, et al. Time-Frequency Characteristics of Large Capacity Air-Gun Array Wavelet and Its Influencing Factors[J]. Journal of Seismological Research, 2017, 40(1): 111-121 DOI:10.3969/j.issn.1000-0666.2017.01.016)
(  0) 0) |
| [19] |
Graaf K L, Brandner P A, Penesis I. Bubble Dynamics of a Seismic Airgun[J]. Experimental Thermal and Fluid Science, 2014, 55: 228-238 DOI:10.1016/j.expthermflusci.2014.02.018
(  0) 0) |
| [20] |
陈浩林, 於国平. 气枪震源单枪子波计算机模拟[J]. 物探装备, 2002, 12(4): 241-244 (Chen Haolin, Yu Guoping. Computer Simulation of Single Air Gun Signature[J]. Equipment for Geophysical Prospecting, 2002, 12(4): 241-244 DOI:10.3969/j.issn.1671-0657.2002.04.004)
(  0) 0) |
2. Key Laboratory of Earthquake Engineering and Engineering Vibration, CEA, 29 Xuefu Road, Harbin 150080, China;
3. Fujian Earthquake Agency, 7 Huahong Road, Fuzhou 350003, China
 2019, Vol. 39
2019, Vol. 39


