2. 朝阳工程技术学校,辽宁省朝阳市凌河街四段483号,122000
针对目前随机有限断层方法模拟地震动明显低于地震记录持时的问题,本文提出相应的改进方案。在大地震诸多震源参数未知的条件下,提出用经验公式确定大地震断层长度、宽度、地震矩和滑动分布等参数,然后用随机有限断层方法预测未来大地震,最后以2016-11-13新西兰MW7.8大地震为例验证本文方法的有效性。为了避免场地效应产生的复杂情况,选择条件相似的场地进行分析(地震记录来自CESMD)。
1 随机有限断层理论随机有限断层方法已经可以用来预测未来大地震[1-2]。在随机有限断层模型中,整个地震断层按一定规则划分为N个子断层,每个子断层尺寸相对于到观测点的距离足够小,可以视为点源,每个点源的地震动用随机方法计算。地震发生时,破裂从某一子断层开始,直到完成整个破裂过程。观测点的地震动由每个子断层产生的地震动按破裂传播的时间延迟叠加形成[3-4]。
观测点的地震动加速度时程a(t)为:
| $ a(t) = \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^n {{a_{ij}}} } \left( {t + \Delta {t_{ij}}} \right) $ | (1) |
式中,l和n分别为断层沿走向和倾向的子断层数目(l×n=N),aij(t)为用随机方法计算出的子断层地震动加速度时程,Δtij为破裂在子断层之间的传播时间,也就是延迟时间,一般认为破裂速度为剪切波速的0.8倍。
每个子断层的ω2谱Aij(f)由式(2)确定[5]:
| $ \begin{array}{l} {A_{ij}}(f) = \left[ {\frac{{C{M_{0ij}}{{(2\pi f)}^2}}}{{1 + {{\left( {{f_{0ij}}} \right)}^2}}}} \right] \cdot \\ \left[ {\exp ( - \pi f\kappa )\exp \left( { - \frac{{\pi f{R_{ij}}}}{{Q\beta }}} \right)/{R_{ij}}} \right] \end{array} $ | (2) |
式中,f为地震波的频率,M0ij、f0ij、Rij分别为子断层的地震矩、动力学拐角频率和震中距,Q为介质品质因子,β为剪切波速,κ为Kappa效应函数,其物理意义是反映地震动高频成分随距离衰减较快的现象,exp(-πfκ)是低通滤波器,C由式(3)确定[5]:
| $ C = \frac{{{R_{{\theta _p}}} \cdot {\rm{FS}} \cdot {\rm{PRTITN}}}}{{4\pi {\rho \beta ^3}}} $ | (3) |
式中,Rθφ为辐射方向因子,FS为自由表面因子,ρ为介质密度,PRTINT=0.707。
目前用随机方法模拟地震动最大的问题是模拟结果的持时大都低于地震记录,其原因是模拟用的地震动持时是震源持时,等于拐角频率的倒数[6]。动力学拐角频率的定义为[5]:
| $ f_{0 i}(t)=N_{R}(t)^{-1 / 3} 4.9 E+6 \beta\left(\Delta \sigma / M_{0 i j}\right)^{1 / 3} $ | (4) |
式中,E为地震释放的能量,NR为破裂的子断层数目,Δσ为应力降。
目前用随机方法模拟地震动持时没有考虑震中距对持时的影响,为此本文采用卢书楠等[7]提出的由地震震级和震中距确定的地震动持时:
| $ D = 0.02{{\rm{e}}^{0.74M}} + 0.3R $ | (5) |
式中,D为地震动持时,M为地震震级,可以由地震震级与矩震级或地震矩的经验关系确定[8]。
式(5)考虑了震中距对持时的影响,而式(4)没有考虑,所以用式(4)模拟的持时都比实际的短。地震动持时与震中距成正比的观测事实也说明用式(5)能更好地反映地震动持时。
子断层划分得足够小才能看成是点源,但式(4)中的拐角频率不能超过模拟的最高频率,如果子断层太多,将导致拐角频率增大,以至于超过模拟的频率(工程感兴趣的频率在12.5 Hz以内),所以子断层的划分应在一定范围内。从地震矩守恒,即子断层地震矩之和应等于整个断层的地震矩角度来看,子断层的划分也应有一定的限制。Beresnev等[9]认为子断层尺寸的变化范围应在5~15 km之间,与美国USGS数据库模型一致。
用随机方法模拟的结果与震源初始破裂点在断层面的位置、断层上的滑动分布关系不密切,其主要取决于随机形成的高斯白噪声[10]。因为每个子断层地震动是用随机方法计算得到的,整个断层地震动是由子断层破裂产生的地震动叠加形成的,子断层之间的地震动传播,也就是地震动从一个子断层传播到另一个子断层是需要时间的,即为延迟时间。延迟时间取决于子断层大小和破裂传播速度,如果子断层长度取15 km,破裂速度取剪切波速0.8倍,剪切波速取3.5 km,那么破裂贯通子断层大约需要5 s。5 s的延迟时间对于相邻子断层产生的地震动的主要部分叠加影响很小,只有对距离大的子断层之间地震动的叠加才会产生较大影响。所以Beresnev等[9]用准随机方法形成的子断层滑动分布预测地震动,虽然子断层的位置和滑动分布与实际存在一定偏差,但并不影响地震动的模拟、预测。因为地震动幅值主要受相邻断层的影响,所以预测地震动时不要求初始破裂点和子断层滑动分布十分精确,甚至可以比较粗略。本文模拟的是地震动的平均效果,而不是针对具体某次地震动的情况,所以子断层形成的地震动对相邻的子断层影响大,对距离较远的子断层影响小。据此,提出根据经验关系[8]确定地震矩、断层长/宽和断层面上的滑动位错,从而实现地震动时程的模拟。
从预测未来大地震的角度看,在确定发震构造的前提下,未来大地震准确的初始破裂位置、断层面的大小和滑动分布是不清楚的,所以强调预测平均效果,用随机方法预测大地震是有实际意义的。Irikura等[11]认为断层初始破裂点多始于断层中间部分,断层面滑动分布中间大、边缘小,因此可以把断层上凸凹体加到断层大致中间位置,实现断层面中间位错大,边缘位错小,从而可以进行地震动的快速模拟、预测。
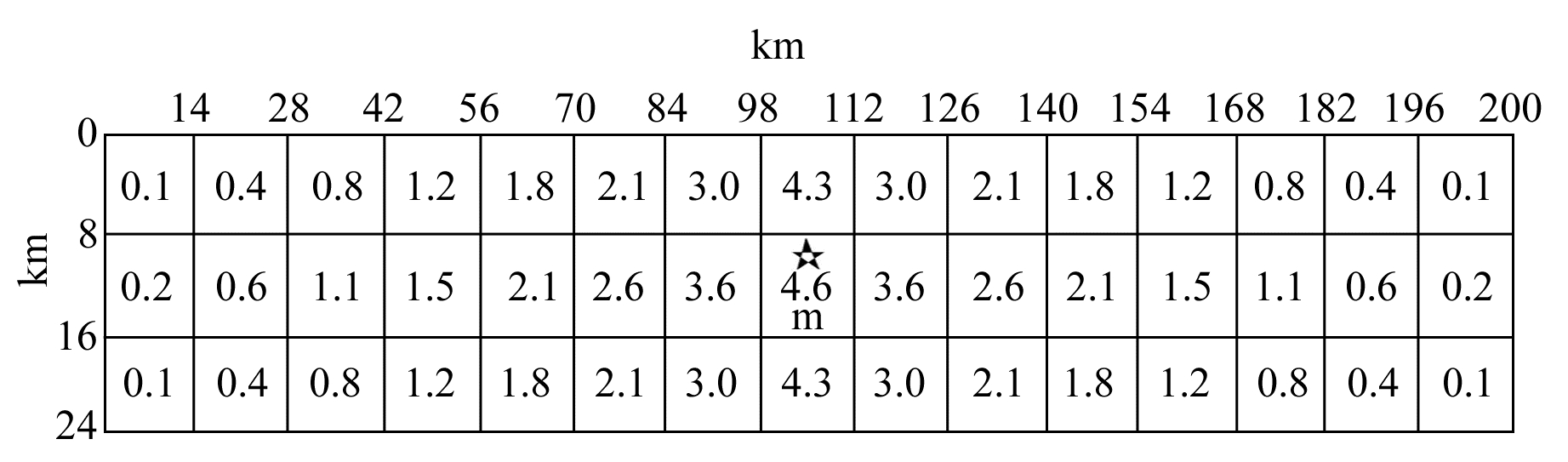
2 数据根据USGS记录,2016-11-13新西兰发生MW7.8大地震,发震时刻为11:02:56(UTC),震中经纬度为173.05°E、42.74°S,震源深度为15.1 km。本文模拟用的12个基岩台站位置如图 1,其地理信息见表 1。表 2中列出了发震构造断层走向和倾向,可以看出,发震构造由4个部分构成,反演资料表明,此次地震断层位错主要发生在第2、3段断层,第1、4段断层产生的位错非常小,可以忽略。资料中没有给出第2、3段断层的几何信息和断层面滑动分布,可以由经验关系计算得出[12],子断层的划分和子断层的滑动分布满足整个地震断层的地震矩守恒。如图 2,断层长200 m、宽24 m,每个子断层长14 m、宽8 m,整个断层分为45个子断层,断层的初始破裂点用五角星表示,整个断层的滑动分布离散化后分配到每个子断层中。

|
图 1 地震记录台站位置 Fig. 1 Locations of seismic station |
|
|
表 1 新西兰MW7.8大地震台站地理信息 Tab. 1 Geographic information of New Zealand MW7.8 earthquake seismic stations |
|
|
表 2 发震构造 Tab. 2 Seismic structure |
|
图 2 断层面的子断层和滑动位错分布 Fig. 2 The subfault and disloction distribution of each subfault |
模拟的地震动持时假定为地震震源持时,区域衰减因子取150×f0.5[13], 几何扩散因子取法为:当震中距小于70 km时,几何扩散因子取1/R;当震中距大于等于70 km,小于等于130 km时,几何扩散因子取1/70;当震中距大于130 km时,几何扩散因子取
|
|
表 3 模型参数 Tab. 3 The model parameters |
震中附近12个台站模拟和记录的水平方向地震动时程如图 3所示,各分图中,最上面的是模拟水平方向的地震动时程,中间和底部的是记录到的2个相互垂直的水平方向的地震动时程,其具体方向在图中有标注。虽然具体某一台站模拟的地震动时程可能与实际有差异,甚至差异较大,但本研究关注的是单台模拟结果与多台站的记录平均结果是否相当[14],模拟地震动的平均效果,才能为建筑物的抗震设防提供基础资料。模拟的平均效果主要体现在地震动峰值代表了相同震中距的峰值加速度平均值。地震动持时的模拟结果与记录之间差异较大,大都是模拟的地震动持时较小。这是因为模拟时用震源滑动持时代替了地震动持时,而地震动持时一定小于实际地震动持时,因为实际地震动持时不仅与震源过程有关,还与传播路径和场地条件密切相关[7]。

|
图 3 12个地震台地震动记录和模拟时程 Fig. 3 Record and simulated time histories at 12 seismic station |
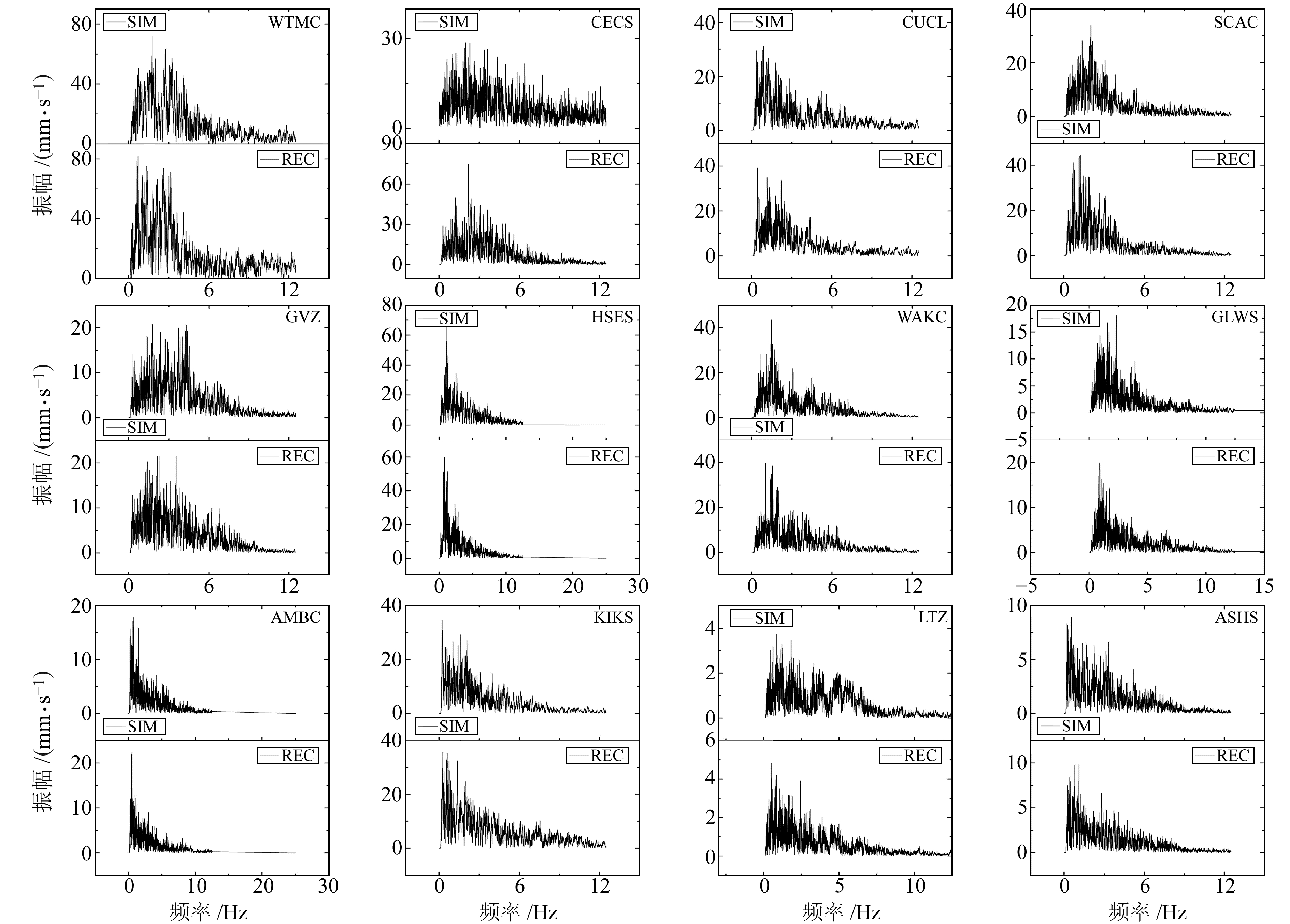
图 4是上述12个台站的模拟频谱和记录频谱,频谱范围主要取工程感兴趣的0~12.5 Hz。各分图中,最上面的是模拟的水平方向频谱,中间和底部是记录到的水平方向2个频谱的平均值。下面研究模拟频谱与记录频谱的差异。
|
图 4 12个地震台站记录和模拟反应谱 Fig. 4 Record and simulated response spectra at 12 seismic station |
定义在一定频率下,模拟频谱与记录频谱幅值之比为模拟误差,简称误差。按照图 2中的滑动分布,取断层附近12个台站在一定频率下的模拟误差平均值,绘制模拟误差随频率的变化曲线,如图 5,曲线频率变化范围为0~12.5 Hz。图中阴影中间部分的曲线是模拟误差随频率的变化,其误差在0.92~1.08之间,表明模拟结果几乎不受频率影响;阴影部分表示95%的置信区间随频率的变化;虚线表示标准差为±1的范围。标准差提供了单一台站预测的不确定性,置信区间提供了模型的平均不确定性,针对多台模拟的平均不确定性小于对单一台站预测的不确定性。

|
图 5 模拟误差随频率的变化(按图 2中的滑动分布) Fig. 5 The variation of the simulation error with the frequency(sliding distribution as shown in figure 2) |
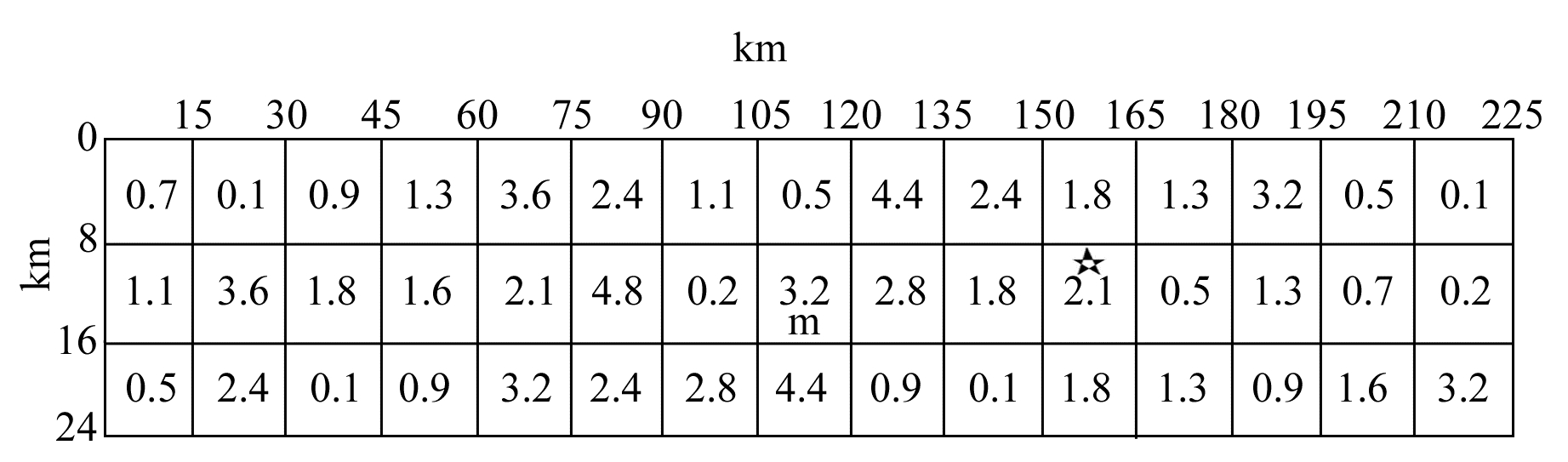
理论上可以掌握活断层发震构造的准确位置,所以通过随机确定断层面初始破裂点和滑动分布能模拟地震动,并与图 5类似计算模拟误差随周期的变化,以确定模拟效果。具体方法为:将图 2中断层的初始破裂点和滑动分布进行准随机分布,因为每个子断层的滑动分布是确定的,子断层和初始破裂点可以随机排列。把图 2中初始破裂点和子断层重新随机分布后,得到如图 6的断层滑动分布。计算12个台站在一定周期下的模拟误差平均值,绘制模拟误差随周期的变化曲线,如图 7。可以看出,与图 5比较,置信区间几乎没有发生变化,标准差也没有增加,12个台站的模拟误差平均值也没有明显的变化,说明在周期0~10 s范围内,有限断层方法模拟结果受断层初始破裂点和滑动分布的影响较小。
|
图 6 准随机形成的子断层滑动位错分布 Fig. 6 The dislocation distribution of subfaults caused by quasi random method |

|
图 7 准随机形成的滑动分布模拟地震动结果误差随周期的变化 Fig. 7 The earthquake error simulated by quasi random slip distribution changes with period |
研究表明,用随机有限断层方法模拟的地震动结果与确定断层面初始破裂位置和滑动分布的关系不密切[9]。据此,在已知发震构造、不清楚断层面初始破裂位置和断层滑动分布的情况下,可以用经验关系[12]确定未来大地震断层的长度、宽度、断层滑动分布等信息,进一步实现用随机方法预测未来地震动。
用随机有限断层方法模拟2016-11-13新西兰MW7.8远场地震动时程和反应谱,定义反应谱模拟幅值和记录幅值比为模拟误差,计算周期0~10 s内的模拟误差随周期的变化。结果表明,12个场地各周期的模拟误差平均值都比较小,模拟误差在0.92~1.08之间,在95%的置信区间与频率无明显关系,且各周期模拟误差的标准差都小于1,表明模拟结果从平均意义上讲精确度较高。
为了进一步证实本文方法的有效性,在已知的发震构造上准随机排列滑动分布和初始破裂点,模拟结果与上文结果比较,其相对误差、95%的置信区间和各周期的标准差范围都没有明显变化,证实了本文提出的预测未来大地震方法的有效性。所以,精确地预测大断层地震动周期在0~10 s范围内频谱平均影响效果不需要掌握十分准确的滑动分布,这一结论与大地震是随机过程的观点一致[2],也说明了地震震源过程和传播路径的复杂性难以用十分准确的概念确定。
本文强调用随机方法模拟地震动的平均效果,无需准确掌握断层初始破裂点和断层滑动分布,但具体某个台站的模拟却可能出现较大偏差。不过这不是本文关注的重点,因为工程上往往关注模拟的结果是否与地震动记录的平均效果相当。本文模拟的地震台站都处于断层一侧,不涉及破裂方向性效应问题,场地都是基岩场地,涉及的路径也可能比较相似,所以模拟的效果较理想。但如果涉及破裂的方向性效应、不同场地条件、表面地形和盆地效应时,需要对随机模拟地震动方法进行修正[15]。
| [1] |
Irikura K. Semi-Empirical Estimation of Strong Ground Motions during Large Earthquakes[J]. Bulletin of Disaster Prevention Research Institute, 1983, 33(2): 63-104
(  0) 0) |
| [2] |
Boore D M, Thompson E M. Revisions to Some Parameters Used in Stochastic-Method Simulations of Ground Motion[J]. Bull Seismol Soc Am, 2015, 105(2A): 1 029-1 041 DOI:10.1785/0120140281
(  0) 0) |
| [3] |
Hartzell S H. Earthquake Aftershocks as Green's Functions[J]. Geophysical Research Letters, 1978, 5(1): 1-4 DOI:10.1029/GL005i001p00001
(  0) 0) |
| [4] |
Atkinson G M, Silva W. An Empirical Study of Earthquake Source Spectra for California Earthquakes[J]. Bulletin of the Seismological Society of America, 1997, 87(1): 97-113
(  0) 0) |
| [5] |
Motazedian D, Atkinson G M. Stochastic Finite-Fault Modeling Based on a Dynamic Corner Frequency[J]. Bulletin of the Seismological Society of America, 2005, 95(3): 995-1 010 DOI:10.1785/0120030207
(  0) 0) |
| [6] |
Boore D M. Stochastic Simulation of High-Frequency Ground Motions Based on Seismological Models of the Radiated Spectra[J]. Bulletin of the Seismological Society of America, 1983, 73(6A): 1 865-1 894
(  0) 0) |
| [7] |
卢书楠, 翟长海, 谢礼立. 汶川地震中强震持时的特征研究[J]. 地震工程与工程振动, 2013, 33(2): 1-7 (Lu Shunan, Zhai Changhai, Xie Lili. Characteristics of Duration of Ground Motion during the Wenchuan Earthquake[J]. Journal of Earthquanke Engineering and Engineering Vibration, 2013, 33(2): 1-7)
(  0) 0) |
| [8] |
Hanks T C, Bakun W H. A Bilinear Source-Scaling Model for M-LogA Observations of Continental Earthquakes[J]. Bulletin of the Seismological Society of America, 2002, 92(5): 1 841-1 846 DOI:10.1785/0120010148
(  0) 0) |
| [9] |
Beresnev I A, Atkinson G M. FINSIM——A FORTRAN Program for Simulating Stochastic Acceleration Time Histories from Finite Faults[J]. Seismological Research Letters, 1998, 69(1): 27-32 DOI:10.1785/gssrl.69.1.27
(  0) 0) |
| [10] |
Beresnev I A, Atkinson G M. Stochastic Finite-Fault Modeling of Ground Motions from the 1994 Northridge, California, Earthquake: Validation on Rock Sites[J]. Bulletin of the Seismological Society of America, 1998, 88(6): 1 392-1 401
(  0) 0) |
| [11] |
Irikura K, Miyake H, Iwata T, et al. Recipe for Predicting Strong Ground Motion from Future Large Earthquake[C]. The 13th World Conference on earthquake Engineering, Vancouver, 2004
(  0) 0) |
| [12] |
Hanks T C, Kanamori H. A Moment Magnitude Scale[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B5): 2 348-2 350 DOI:10.1029/JB084iB05p02348
(  0) 0) |
| [13] |
Boore D M. Stochastic Simulation of High-Frequency Ground Motions Based on Seismological Models of the Radiated Spectra[J]. Bulletin of the Seismological Society of America, 1983, 73(6A): 1 865-1 894
(  0) 0) |
| [14] |
Boore D M. Simulation of Ground Motion Using the Stochastic Method[J]. Pure and Applied Geophysics, 2003, 160(3-4): 635-676
(  0) 0) |
| [15] |
Boore D M. Determining Generic Velocity and Density Models for Crustal Amplification Calculations, with an Update of the Generic Site Amplification for VS(Z)=760 m/s[J]. Bulletin of the Seismological Society of America, 2016, 106(1): 313-317 DOI:10.1785/0120150229
(  0) 0) |
2. Chaoyang Engineering Technical School, 483 Linghe Street, Forth Section, Chaoyang 122000, China
 2019, Vol. 39
2019, Vol. 39

